Использование МатАнализа в компьютерных играх (часть 3)
Ключевые слова: DPS (DamagePerSecond); Wolfram Mathematica; дискретность и непрерывность; матанализ; заработок игровой валюты в компьютерных играх; паки ArcheAge.
Введение
Всем знакомы однотипные вопросы в школьных задачах по математике про мотоциклиста выехавшего из пункта А в пункт Б, которые вызывают скуку, отвращение, или просто безразличие. Вопросы, которые вызывают, все что угодно кроме интереса к изучению математики. Очевидно что, гораздо больший интерес и больше эмоций вызывают вопросы типа:
1) «как он смог меня одолеть в игре, если у моего персонажа и здоровья больше и DPS (Damage Per Second) выше?!»
2) «как быстрее всего заработать голду (игровую валюту), чтобы сделать своего персонажа сильнее?!»
На самом деле эти игровые вопросы очень похожи на классические школьные задачи. Разница лишь в том, что есть заинтересованность в получении ответа на игровые вопросы, есть цель, ради которой хочется решить эти задачи. К сожалению, очень многие преподаватели в школах и вузах совершенно не умеют заинтересовать обучаемых в получении конкретной информации, новом методе решений математических задач, доведении их до ответа. Но раз уж игры вызывают этот самый интерес, то грех не воспользоваться заинтересованностью в игре, для пробуждения интереса к математическому анализу.
Вот две задачи, которые являются лишь переформулированными вышеупомянутыми вопросами.
1) Петя и Коля решили помочь дедушке наполнить две одинаковые пустые бочки водой из колодца. Петя таскал воду в 5-и литровом ведре и на один заход к колодцу и обратно к бочке тратил 3 минуты, а Коля в 8-и литровом и на один заход тратил 5 минут. Каждый заполнял свою бочку. Кто из мальчиков быстрее заполнит свою бочку, если а) объём бочки 60 литров? б) если объем бочки 56 литров? (начали мальчики одновременно)
2) Два купца Семён и Добрыня покупают у крестьян по 10 пудов мёда за 5 золотых и везут его на продажу в соседние города. Добрыня везёт в ближайший город и продаёт там за 8 золотых, весь путь до города и обратно у него занимает 2 дня. Семён же, желающий продавать своё мёд как можно дороже, не ленится и везёт его ещё дальше, тратя на весь путь 3 дня, и продавая мёд в другом городе за 10 золотых. Кто же из купцов заработает больше за 360 дней непрерывной работы? Как изменится ситуация, если оба купца вынудят крестьян снизить цену на мёд до 3 золотых?
Разбор этих задач, описанный ниже, поможет ответить на животрепещущие вопросы игры ArcheAge (и других) про «паки» и DPS. А также позволит задуматься над такими понятиями как «дискретность» и «непрерывность», а так же над таким, казалось бы, очевидным вопросом как «прибыль».
Парадокс ДПС
Для того чтобы было легче разобраться с задачей про бочку, очень удобно нарисовать всё что происходит на графике. Красным цветом обозначим Петю, а зелёным Колю. Получим две лесенки. Бочка Коли и бочка Пети заполняются дискретно, длина ступенек равна времени похода до колодца и обратно к бочке, а высота равна количеству принесенной воды в литрах. На большей части полученного графика красная лесенка выше зелёной, но вот на некоторых участках выше зелёная.
Чтобы наполнить бочку объёмом 60 литров, используя 5 литровое ведро, нужно 12 раз сбегать с этим ведром до колодца. В итоге Петя потратит 3 минуты*12раз=36 минут. Коле же, с его 8 литровым ведром, нужно 60/8=7.5раз. Получаем нецелое число. За 7 походов Коля принесёт только 7×8=56 литров, что меньше чем нужно. А если ещё раз Коля пойдет за водой, то принесет уже 64 литра, что даже больше чем надо. В итоге Коле потребуется 8раз*5 минут=40 минут, то есть Петя раньше наполнит свою бочку.
Ситуация меняется если надо было принести 56 литров. Для этого Коле нужно сбегать 56/8=7 раз, и займёт это 35 минут. Пете же потребуется 56/5=11.2раза, но так как важно именно целое число, то на самом деле Пете потребуется сходить 12 раз и займёт это 12×3=36 минут. В данном случае Петя наполнит свою бочку позже Коли.
Получается вот такая странная ситуация, что ответ на вопрос кто же быстрее заполнит бочку, зависит не только от мальчиков, но и от размеров бочки. Причём если посмотреть на график, то мест где графики пересекаются довольно много. Более того, можно даже сделать бочку Пети 55.9 литра, то есть меньше чем у Коли, а он всё равно заполнит её позже. Ещё удивительнее этот факт становится, если рассчитать среднюю скорость заполнения бочки Петей и Колей. У Пети средняя скорость равна 5/3=1.666 литра/минуту, а у Коли 8/5=1.600 литра/минуту. Коля может даже начать позже на полминуты, и всё равно Петя будет вторым.
То есть у Пети и скорость заполнения больше, и бочка меньше, и начал он раньше, а он всё равно заполнит свою бочку позже, чем Коля заполнит свою.
Вот такой парадоксальный результат получается именно из-за того, что процесс заполнения бочки носит дискретный характер.
Если же рассматривать случай когда два противника в игре наносят друг другу удары с разной силой и разной скоростью, то эта ситуация будет аналогична бочкам и ведрам, которую мы уже рассмотрели. И как было показано выше, не всегда стоит полагаться в оценке силы вас и вашего противника на так называемую DPS, то есть на среднюю скорость нанесения повреждений.
Совсем ли DPS неприменима? Не совсем. В некоторых случаях она вполне адекватно описывает ситуацию.
Для каждой лесенки, можно построить две параллельные прямые, которые будут проходить через верхние угловые точки и через нижние.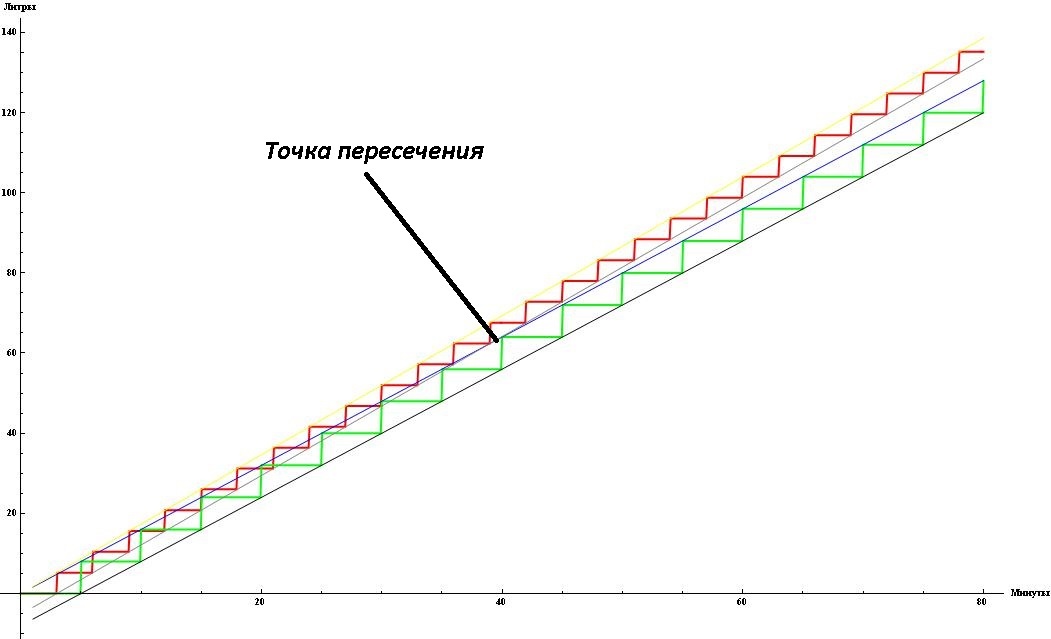
Та лестница, у которой DPS выше, после какого-то момента всегда будет выше второй. А этот момент можно найти как пересечение нижней прямой лестницы большего DPS, с верхней прямой лестницы меньшего DPS. Вот формулы для этих двух прямых.
fDPSL1(t)=(DPH1/Period1)*(t-Period1);
fDPSH2(t)=(DPH2/Period2)*t;
DPH1 и DPH2 это сила удара (объём ведра) за период Period1 и Period2 соответственно. DPH1/Period1=DPS1. А пересечение этих прямых происходит в момент
T = Period1/(1-DPS2/DPS1)
Из этой формулы видно, что влияние дискретности ситуации, и возможность возникновения связанных с дискретностью парадоксов, зависит от двух факторов. Первый фактор, это примерное равенство DPS обоих противников. В таком случае, знаменатель обращается в нуль, и время прекращения влияния дискретности ситуации стремится к бесконечности. Второй фактор, это период ударов того, у кого DPS выше. Чем выше частота ударов, тем меньше период, а значит и время прекращения влияния дискретности будет меньше.
Ещё из формулы для верхней прямой
fDPSH2(t)=(DPH2/Period2)*t
видно, что это просто формула графика урона от времени при фиксированном DPS.
fDPSH2(t)=DPS2*t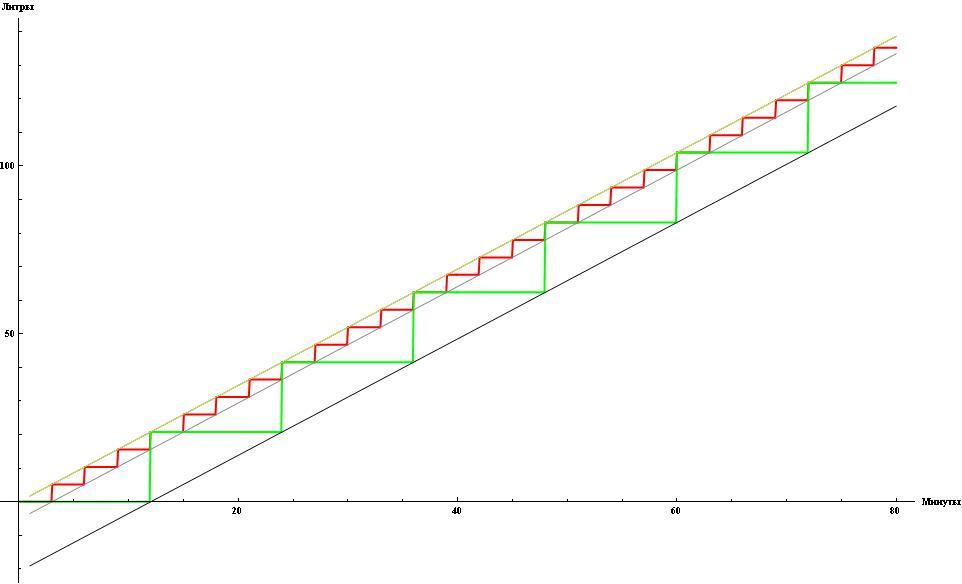
Если у противников DPS одинаков, то в лучшем положении окажется тот, у кого МЕНЬШЕ и сила и период ударов. В предельном случае, если период ударов стремится к нулю, то лесенка превратится в «непрерывную» прямую вида fDPSH (t)=DPS*t. И данная прямая является наиболее выгодным вариантом при фиксированной PDS.
Таким образом, если есть выбор увеличить на N% силу удара или увеличить на те же N% частоту удара, то выгоднее увеличивать частоту, хотя в обоих этих случаях DPS увеличится одинаково. Однако, как показывает практика, многие в силу каких-то интуитивных заблуждений предпочитают увеличивать силу удара.
Ловушка жадности
Задача про купцов решается аналогичным образом. Семён за одну поездку тратит 5 золотых, получает 10, итого прибыль 5 золотых за 3 дня. Добрыня за 2 дня получает 3 золотых. За 360 дней Семён сделает 120 поездок и заработает 600золотых. Добрыня же заработает 360/2×3=540 золотых. В итоге Семён правильно делает, что возит дальше, он заработает больше Добрыни. Если же Семён и Добрыня договорятся, и найдут способ заставить крестьян продавать им мёд по 3 золотых. То тогда Семён за одну поездку получит уже 7 золотых, а Добрыня 5. За 360 дней Семён получит 360/3×7=840, а Добрыня 360/2×5=900. То есть Добрыня за 360 дней заработает больше Семёна, несмотря на то, что продавать будет свой товар дешевле.
В экономике есть такое понятие как рентабельность — отношение прибыли от реализации к себестоимости реализованной продукции.
Так вот, если рассматривать отношение прибыли к затратам, то у Семёна рентабельность может показаться выше. За одну поездку потратив 5 золотых, он получает 5золотых прибыли. Добрыня же за 5 золотых получает лишь 3 золотых прибыли. Но с таким подходом, как можно заметить, совершенно не учитывается время, а его по хорошему нужно вставлять в себестоимость как зарплату Семену и Добрыни за перевозку. То есть помимо тех денег, что они вкладывают, нужно учитывать и то время, что они тратят. И когда идёт речь о получении прибыли, о способе заработка, то нужно обязательно принимать во внимание не только саму прибыль, полученную в результате каких-то действий, но и затраченное на них время.
Что бы стало яснее, как же так получается, что продавать по более низкой цене бывает выгодно, снова нарисуем график. На графике показана зависимость получаемой прибыли в единицу времени от себестоимости товара для 3 разных случаев. В каждом из случаев товар и его себестоимость будут считаться одинаковыми, а вот цена продажи и время на перевозку будут различны. Графики строятся по простой формуле
F[Себестоимость]=(ЦенаПродажи — Себестоимость)/Время перевозки
Примеры времени и цен продажи взяты из игры ArcheAge. Время измеряется в минутах, а цены в «голде».
В первом случае ЦенаПродажи =8 г, Время =6 минут, во втором ЦенаПродажи =11 г, Время = 10 минут, и в третьем случае ЦенаПродажи =13 г, Время =16 минут
В сети можно найти таблицу цен продажи всех возможных грузов в игре ArcheAge, например тут
Но, тем не менее, в этих таблицах не указаны расстояния до мест продажи, что конечно является большим недостатком.
Реальные же затраты на сырье, которое необходимо для изготовления товаров, в игре достаточно сильно варьируются, в силу колебаний игрового рынка. Цены, вообще говоря, выставляются игроками, в том числе и так называемые «очки работы», которые необходимы для производства товара, и которые тоже можно покупать на «рынке». Себестоимость в данном примере приблизительно 7 г, но может быть и значительно дороже.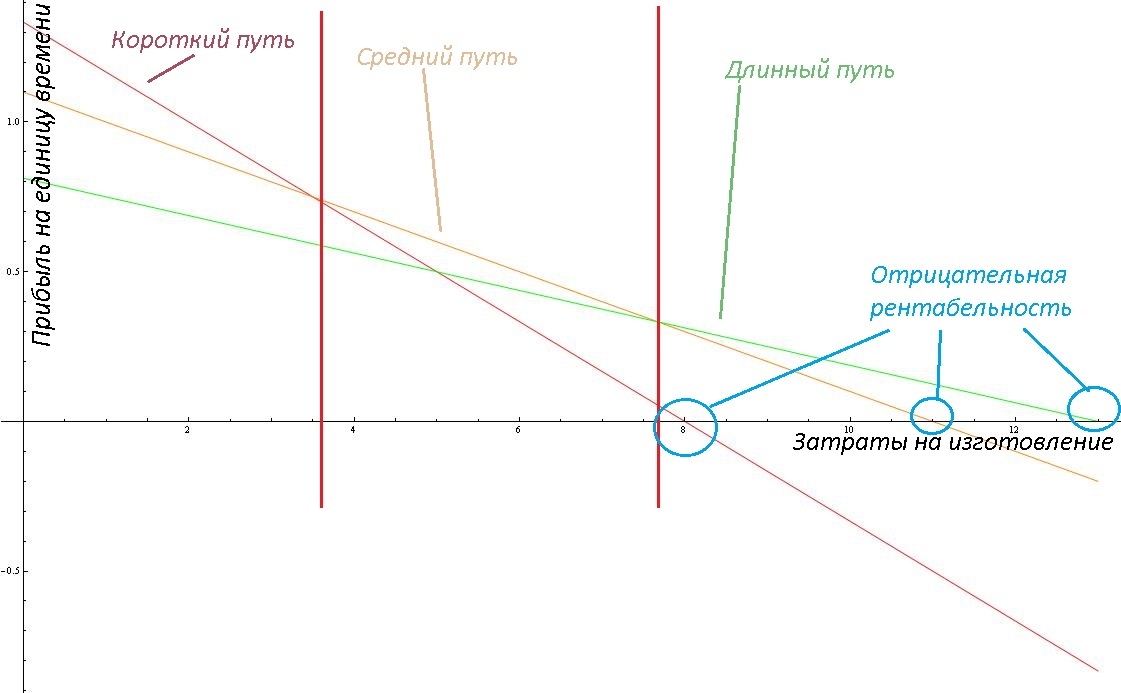
Пониманию некоторой задачи, процесса, очень часто помогает рассмотрение крайних случаев. Если себестоимость товара равно нулю, то вся прибыль на единицу времени определяется временем, которое будет затрачено на перевозку. В общем случае все 3 прямые могут и не пересекаться, но в данном конкретном случае, при низкой себестоимости выгоднее возить в ближайшее место продажи. Если же себестоимость высокая, то она может быть выше чем цена продажи в ближайших точках, а это значит, что вы будете работать с отрицательной рентабельностью, то есть тратить больше, чем получаете. И тогда единственной возможностью заработать хоть сколько-то будет продажа в самом удалённом месте, где цена продажи выше себестоимости. Но при слишком высокой себестоимости, даже там продавать становится не выгодно. Так же существует и промежуточный вариант, когда выгоднее всего возить на среднее расстояние.
Стоит отметить, что эффекты, связанные с «дискретностью» получения прибыли, тут тоже естественно присутствуют. Принцип разбора этих эффектов, аналогичен тому, что был рассмотрен выше.
Когда такое пытаешься рассказать игрокам, очень часто получаешь в ответ «Лол?! Я знаю, что нужно делать! Чё ты меня учишь?!». Люди упорно стремятся продать свой товар как можно дороже, и совершенно не обращают внимания на то, сколько времени они на это тратят. Время же можно выражать в валюте и использовать уже эту «цену времени» в себестоимости, и тогда всё становится гораздо понятнее. Но очень часто встречаются те, кто ради 1 голды готовы везти ещё дальше, тратя время с гораздо меньшей эффективностью. В итоге пожадничав, они больше теряют.
И что самое интересное, даже те, кто знают об этих тонкостях, очень часто поддаются внутреннему сиюминутному соблазну, слепой ошибочной интуиции, и коварному и опасному чувству алчности, и всё равно прут туда, где объективно не выгодно продавать, но зато где они увидят, что цена продажи их товара выше. Психофизиология — против неё даже матан порой не работает. Зато эту особенности человеческого восприятия любят использовать в своих целях все кому не лень, паразитируя на жадинах.
Wolfram Mathematica
Wolfram Mathematica это черезвычайно мощный инструмент для решения разнообразных задач любой сложности. Однако не стоит думать, что раз Mathematica столько всего может, то она чрезвычайно сложна в использовании. На самом деле, я её очень часто использую просто как очень удобный, но и очень продвинутый калькулятор. При этом нет необходимости писать код алгоритмов. Чтобы нарисовать графики, или быстро сделать интерактивное окно, с полями ввода, ползунками и рисовалкой функций в реальном времени, то хватит несколько простых команд, которые очень подробно, на куче примерах описаны во встроенном хелпе.
Вот пример кода для отрисовки графиков прибыль/себестоимость.
a = {{6, 8}, {10, 11}, {16, 13}};
f[i_, x_] := (a[[i]][[2]] - x)/a[[i]][[1]];
Plot[{f[1, x], f[2, x], f[3, x]}, {x, 0, 13},
PlotStyle -> {Red, Orange, Green}, PlotRange -> All]
И пример кода для вот такого удобного окошка для отрисовки дискретных процессов. Можно менять параметры и сразу сравнивать полученные результаты на графике.
TotalD[DPH_, CD_, tDelay_, tDuration_] :=
Table[{n, DPH*(Quotient[n - tDelay, CD])}, {n, 0, tDuration,
tDuration/1000}];
(*Дискретный график наносимых повереждений участником боя через \
единицу времени*)(*Quotient даёт нам целое число количества ударов \
нанесеннного за некратное перезарядке время*)
DiffD[DPH1_, CD1_, tDelay1_, DPH2_, CD2_, tDelay2_, tDuration_] :=
Table[{n,
DPH2*(Quotient[n - tDelay2, CD2]) -
DPH1*(Quotient[n - tDelay1, CD1])}, {n, 0, tDuration,
tDuration/
1000}];(*Разница количества повреждений нанесенных двумя \
участинками*)
fDPSH[t_, DPH_, CD_,
tDelay_] := (DPH/CD)*(t -
tDelay);(*fDPSH и fDPSH это прямые которые "ограничевают" граффик \
наносимых повреждений. Можно сказать что это оценки сверху и снизу*)
fDPSL[t_, DPH_, CD_, tDelay_] := (DPH/CD)*(t - CD - tDelay);
Manipulate[
Column[{
Row[{
Row[{"DPS1=", Dynamic[N[DPH1/CD1]]}, Frame -> True,
FrameStyle -> {Red, Red}],
Row[{Dynamic[
If[DPH1/CD1 == DPH2/CD2, " EQUAL ",
If[DPH1/CD1 > DPH2/CD2, " MORE THAN ", "LESS THAN "]]]}],
Row[{"DPS2=", Dynamic[N[DPH2/CD2]]}, Frame -> True,
FrameStyle -> {Green, Green}]
}],
Show[{
Plot[
{fDPSL[t, DPH1, CD1, Delay1],
fDPSH[t, DPH1, CD1, Delay1],
fDPSL[t, DPH2, CD2, Delay2],
fDPSH[t, DPH2, CD2, Delay2]},
{t, 0, Duration},
PlotStyle -> {Darker[Orange], Darker[Orange], Darker[Blue],
Darker[Blue], PlotRange -> All}
],
ListLinePlot[
{TotalD[DPH1, CD1, Delay1, Duration],
TotalD[DPH2, CD2, Delay2, Duration],
DiffD[DPH1, CD1, Delay1, DPH2, CD2, Delay2, Duration]},
PlotStyle -> {Red, Green, Gray}, PlotRange -> All]
}, PlotRange -> All]
}],
{{DPH1, 10, "Value1"}, 0, 100, Appearance -> "Open"},
{{CD1, 0.8, "Period1"}, 0, 20, Appearance -> "Open"},
{{Delay1, 0}, -2, 2, Appearance -> "Open"},
{{DPH2, 8, "Value2"}, 0, 100, Appearance -> "Open"},
{{CD2, 0.7, "Period1"}, 0, 20, Appearance -> "Open"},
{{Delay2, 0}, -2, 2, Appearance -> "Open"},
{{Duration, 10}, 2, 1000, Appearance -> "Open"},
ControlPlacement -> {Right, Right, Right, Right, Right, Right, Right,
Right}
]
Нужно просто скопировать код в пустое окно Wolfram Mathematica и нажать Shift+Enter. Результат вы получите в том же окне.
Выводы
Интернет не всезнающ. Гайды, рецепты, методички на все случаи жизни в нём не найти. В каждом конкретном случае всё равно доработка, модернизация общеизвестных методов позволит достичь лучших результатов. Но для этого требуются анализировать ситуацию, и на основе известных данных синтезировать новые методы. Но такие навыки сами собой не возникнут, им нужно обучаться, тренировать. А это порой бывает делать скучно и лениво. Выхода два: либо пытаться процесс обучения в школе или в вузе, который зачастую кажется бессмысленным и скучным, делать осознанным, осмысленным и интересным, либо, занимаясь чем-то интересным и увлекательным, находить в этом интересные моменты, анализировать их и пытаться решить поставленные в игре задачи, как полноценные задачи по математике.
Если препод вам попался скучный и безынициативный, то это не повод не заниматься МатАнализом. В конце концов, оправдываясь плохим преподом, вы свою жизнь интереснее, а себя успешнее не сделаете.
