Использование МатАнализа в компьютерных играх (часть 2)
Ключевые слова: Задача о коллекции; Wolfram Alpha; Wolfram Mathematica; числа Стирлинга второго рода; матанализ; теория вероятностей; мат ожидание; медиана; квантиль; компьютерные игры; коллекция вкладышей; функция распределения случайной величины; плотность вероятности, ArcheAge.
Введение
Когда остается заполучить только три из ста предметов для того чтобы собрать всю коллекцию (вкладышей жвачек БомБимБома или Турбо, или набора тяжелых доспехов для персонажа компьютерной игры), то огонь в глазах и ожидание чуда вытесняют и логику и разум и попытки математического анализа из головы напрочь. Есть только одна мысль «Ещё чуть-чуть и я заполучу оставшееся! Я соберу всю!». В это время, родные и друзья, этого одержимого коллекционера озадачены лишь только одним вопросом — «А, чуть-чуть, это сколько?!». Сколько маме нужно купить ещё ненавистных жвачек, или сколько нужно ещё девушке сидеть одной, пока её парень не выбьет с монстров в игре «редчайшие трусы Баала»?!
Ответить на вопрос «сколько нужно купить жевательных резинок, чтобы собрать полную коллекцию из N-штук вкладышей» сходу довольно сложно, даже если пользоваться Яндексом, потому, что сложно сформулировать сам запрос для «обычного» поисковика. Попытка решения задачи самостоятельно обычно ставит людей в тупик — не понятно, с какой стороны к ней подступиться.
В данной статье будут рассмотрены три вопроса: Как подходить к задачам, которые не понятно на первый взгляд как решать? Каким поисковиком пользоваться для того чтобы получать научные ответы на научные вопросы (а не получать предложения купить формулу квадратного уравнения на eBay)? И конечно, сколько же нужно купить жвачек, чтобы собрать коллекцию вкладышей?
Навигация по статье
Статья получилась довольно большой. Поэтому в тех местах, где можно что-то пропустить, я буду об этом сообщать. В таких главах будет рассматриваться не решение задачи, а те понятия и принципы которое используются при её решении. Если же станут интересны подробности, то можете перечитать пропущенные места позже. С формулировкой задачи стоит ознакомиться, а вот далее, те, кто хочет поскорее ознакомиться с ответом, могут сразу перейти к результатам. Советую, однако, отдельно ознакомиться с главой посвященной Alpha Wolfram.
Так же для удобства, привожу полный список глав.
- Постановка задачи
- Парни, девушки и шары
- Математическое моделирование одержимого коллекционера
- Любопытная таблица
- Азъ есмь Alpha Wolfram
- Математический детектив
- Триста лет тому назад
- Три строчки
- Две сущности
- Средняя температура пациентов и средняя зарплата врачей
- Там, где прямо не пролезем, мы пройдём бочком
- Wiki-больство какое-то
- Результаты
- День рождения и банка плесени
- Выводы
Постановка задачи
Чтобы было понятно и тем, кто любит математическую строгость, и тем, кто с ней не знаком, сформулирую задачу о коллекции двумя способами.
- (Через язык знакомый с детства) Пусть каждая жвачка содержит с равной вероятностью один из K вкладышей. Какова вероятность того что купив N жвачек, мы соберём всю коллекцию вкладышей (у нас будет K уникальных вкладышей)?
- (Более научным языком) Пусть дано множество из K элементарных исходов (все исходы равновероятны). Какова вероятность того, что после N проведенных экспериментов каждое событие произойдет хотя бы один раз?
Сразу проясним ряд моментов, которые в дальнейшем нам помогут в решении. Во-первых, для простоты все элементы коллекции будем нумеровать от 1 до K, и таким образом иметь дело просто с числами. Во-вторых, нашими элементарными исходами будут последовательности чисел длинной N, состоящие из K различных чисел. Например, если K=3 и N=5, то последовательности {3,3,1,2,3},{1,2,3,3,3},{3,3,1,1,1} одни из возможных исходов, при этом порядок элементов имеет значение. Если в такой последовательности все K чисел встречаются, хотя бы один раз — значит это «удачная» для нас последовательность, если не встречается, хотя бы одно число ни разу, значит последовательность для нас не удачная. При этом любая возможная последовательность равновероятна. В-третьих, мы всегда можем посчитать количество всех возможных последовательностей из K чисел, длиной N элементов, при условии, что порядок имеет значение. Это количество равно K^N. В-четвертых, вероятность сбора коллекции за N шагов, равна отношению «удачных» последовательностей к общему количеству, то есть к K^N. Таким образом, можно искать либо вероятность, либо само количество «удачных» последовательностей — как будет удобнее, одно всегда можно получить из другого.
Парни, девушки и шары
Те, у кого не возникло вопросов касательно «порядок имеет значение» и «количество равно K^N», а так же кто помнит что такое «факториал» и «C из n по k», эту главу можете пропустить и перейти к следующей. Для тех же, кто основательно подзабыл комбинаторику, или ещё не был с ней знаком, рассмотрим основные моменты, которые нам пригодятся.
История комбинаторики хоть и уходит корнями в глубокую древность, всё же активно развивалась благодаря гамерам. Ну, может Кардано, Галилей, Ферма Паскаль и остальные великие умы мира сего сами и не были заядлыми гамерами (хотя не факт не, факт), но как минимум гамеры их конкретно донимали вопросами об играх, про стратегии победы, просили гайды писать. Конечно, тогда больше как-то в кости да карты играли, любителей азартных игр с танками или магией было как-то не очень много. С одним был дефицит, а за другое сжигали. Но активно применявшись к анализу головоломок и азартных игр, комбинаторика оказалась исключительно полезной для решения практических задач почти во всех разделах математики. Кроме того, комбинаторные методы оказались полезными в статистике, программировании, генетике, лингвистике и многих других науках уже много времени спустя. Википедия ЗЛО (я об этом ещё не раз вспомню), но обзорные вещи не связанные с формулами там читать физически возможно, а вот доверять не стоит. Тем не менее, можете ознакомиться со статьёй «История комбинаторики»
Я пока искал различные материалы по комбинаторике, наткнулся на сайт, а точнее на один из документов с этого сайта. Понравился язык, которым написано, можете ознакомиться с комбинаторикой там. Я бы, в общем-то, и не вспомнил про этот сайт, если бы не одно «но». Там есть задача про траекторию. Мне она очень понравилась, показалась интересной, и вот глядя на неё, у меня родилась идея, как решить задачу про коллекцию, но об этом позже.
Вот основные факты из комбинаторики, которые нам пригодятся.
1.) Сколько всего существует N -значных чисел в системе счисления с основанием K? Сколькими способами можно разместить на N креслах представителей K наций? Сколькими способами можно раскрасить N квадратов, если есть фломастеры K различных цветов? Сколькими способами можно заполнить N ящиков разноцветными шарами, если количество различных цветов K и в каждый ящик влезет только один шар?
Ответ на все эти вопросы один — «Размещение с повторениями». В случае с шарами, в первый ящик мы можем положить шар любого из K цветов. То есть у нас K вариантов засунуть один шар в первый ящик. Во второй ящик мы тоже можем засунуть шар K способами. Вариантов же заполнения первого и второго ящика шарами уже будет K* K= K^2. Так получается потому, что для каждого варианта заполнения первого ящика может быть любой из K вариантов заполнения второго ящика. Если же ящиков у нас N то значит, вариантов будет K^N.
2.) Сколько всего существует N -значных чисел в системе счисления с основанием N, таких, что каждая цифра в числе встречается ровно один раз? Сколькими способами можно разместить на N креслах представителей N наций, так чтобы сидел представитель каждой нации? Сколькими способами можно раскрасить N квадратов, если есть фломастеры N различных цветов, так чтобы каждый фломастер был использован (без перекрашиваний конечно)? Сколькими способами можно заполнить N ящиков N пронумерованными шарами?
Ответ на все эти вопросы один — «Перестановка». Случаи с шарами и с цифрами, в общем-то, идентичны даже в своей формулировке. На первое место мы можем поместить любой из N шаров. На второе место любой из оставшихся N-1 шаров, на третье любой из оставшихся после заполнения первых двух мест N-2 шаров. И так далее до последнего. Получается, мы имеем произведение N*(N-1)*(N-2)*(N-3)*… *(N-(N-2)) *(N-(N-1)). Вот такое произведение всех натуральных чисел от 1 до N и называется факториалом. А обозначается оно как «N!». Да, восклицательный знак, это и есть обозначение факториала или произведения всех натуральных чисел от 1 до N. Встречается крайне часто везде и всюду, а учитывая, что писать его в виде произведения довольно долго, решили упростить и сократить запись до значка восклицательного знака. Про факториал есть старый анекдот, который любят рассказывать преподаватели.
На экзамене по матану лектор просит студента разложить экспоненту в ряд Тейлора.
Студент: Один плюс икс разделить на ОДИН (произносит громко и торжественно) плюс икс в квадрате разделить на ДВА (также громко) плюс икс в кубе разделить на ТРИ
Лектор: Хорошо, хорошо, всё правильно, только, зачем вы так кричите?!
Студент: Ну, так восклицательный знак же!!!
Стоит отметить, что факториал от нуля будет 1. 0!=1
3.) Сколькими способами можно заполнить K ящиков N пронумерованными шарами? (шаров больше чем ящиков) У вас есть N билетов в кино и K подруг. Сколькими способами вы можете раздать билеты вашим подругам? (билетов больше чем подруг)
Ответ на эти вопросы — «Размещение БЕЗ повторений». Однако решение аналогично не первому пункту, а второму. На первое место мы можем поместить любой из N шаров. На второе место любой из оставшихся N-1 шаров, на третье любой из оставшихся после заполнения первых двух мест N-2 шаров. И так далее до тех пор, пока не кончатся ящики. А значит, произведение будет N*(N-1)*(N-2)*(N-3)*… *(N-(K-1)). То есть произведение всех натуральных чисел от K+1до N. Но такое произведение можно расписать в виде N*(N-1)*(N-2)*(N-3)*… *(N-(K-1)) * (N-K)! / (N-K)! =N!/ (N-K)! Что, в общем-то, значительно короче.
4.) Последний пункт про то, почему порядок может иметь или не иметь значение. И что такое «C из n по k».
Предположим у вас есть УАЗик, и вы собрались поехать с друзьями (только парни, без девушек) на рыбалку. В УАЗик может влезть K человек. А всего у вас друзей N. Все, кто в ваш УАЗик не влезут, поедут на других машинах. Сколько есть вариантов заполнения УАЗика вашими друзьями? Сколько существует способов из 20(N) ваших знакомых который сейчас онлайн собрать команду 5 человек (K) чтобы часок поиграть в доту? (Тут конечно есть нюанс — считать вас или нет, но не будем на этом заморачиваться)
В чём различие этого примера от всех предыдущих? В том, что порядок не имеет значения. Кто, как и где будет сидеть в УАЗике, или кого вы первого, а кого второго позовете в команду, роли не играет ни какой. Главное это состав, а кто там на каком месте уже не важно. Если бы порядок имел значение, то это был бы в точности предыдущий вариант, то есть ответ был бы N!/ (N-K)!. Но нам порядок не важен. А про порядок у нас был пример 2) с факториалом. То есть N!/ (N-K)! нужно разделить на K!, и тогда случаи, которые отличались лишь последовательностью, но были одинаковы по составу, «схлопнутся в один вариант». Например, пусть есть 3 человека и 2 места. Тогда все возможные варианты. Для примера 3 будут {1,2},{1,3},{2,1},{2,3},{3,1},{3,2}. То есть 6 вариантов. 3!/(3–2)!=3!/1!=3!=6. Но в нашем примере с УАЗиком (двухместный правда сейчас уже УАЗик) не важна последовательность и поэтому варианты типа {1,2} и {2,1} одинаковы. Ну, действительно, Петя и Вася в УАЗике или Вася и Петя — разницы нету. Главное что они двое едут в нём. Получаем, что ответом для пункта 4, в котором порядок не имеет значения, будет формула N!/ (N-K)!/ K! И называются такие случаи, когда порядок не важен, а важен лишь состав «Сочетанием из N по K». Есть ещё одно название у этой чудо-формулы — «Биномиальный коэффициент». Но чаще всего называется это «C из n по k». («Цэ из эн по ка»). Обозначается соответственно буквой C с нижним и верхним индексом n и k соответственно. Биномиальный коэффициент имеет самое непосредственное отношение к широко известному «биному Ньютона». Сложного в нём ничего нет, можете прочитать про него, где захотите (Только википедию главное не читайте). Бином Ньютона и биномиальные коэффициенты по сути своей довольно просты, но вот тот факт, что они вдруг внезапно оказываются применимы в неимоверно большом количестве разнообразных ситуаций, создаёт этакий мистический ореол и подозрение что это всё неспроста. Хотя сложного там ничего нет, зато много чего интересного
Этих знаний из комбинаторики на данном этапе будет достаточно, остальное будет пояснено по ходу дела.
Математическое моделирование одержимого коллекционера
Когда я первый раз попробовал решить задачу аналитически, пытаясь честно посчитать (не перебором конечно, а формулами) все возможные удовлетворяющие условиям последовательности, у меня признаюсь ничего не вышло. Точнее сказать путь рассуждений был довольно логичным, но в итоге я приходил к необходимости записи гигантской суммы сумм, свернуть которую во что-то компактное не представлялось возможным.
В случаях, когда понятны основные принципы некоторого процесса, но при этом не можем получить вразумительный и удобоваримый закон, описывающий этот процесс (когда понимаем что и как происходит, а вот формулу для всего этого дела выписать не получается), то можно пойти от обратного — смоделировать этот процесс, получить численное решение и попытаться проанализировать ответ. Например, используя величайший из методов анализа — «Метод Пристального Взгляда». После чего вполне возможно новые полученные данные, идеи, мысли подскажут нам пути решения.
Это как подсмотреть ответ в задачнике, и потом под него подогнать решение. Мы в своё время пользовались этим, но при этом сами себя не одобряли за такое. Однако, семинарист по физике (он же и лектор был) объяснил нам, что это абсолютно нормально, и более того, физика в какой-то мере это «искусство подгонки». Очень часто сначала открывается некоторое новое явление, а затем его пытаются объяснить — то есть как бы решение, теоретическое обоснование явления пытаются подогнать под экспериментальные данные. Тогда нам это было не совсем понятно — мы привыкли что нужно «решать задачи честно». Только вот теоретическое построение гипотез с последующей экспериментальной проверкой, это одно, но вот обратные задачи встречаются порой даже чаще. И одно без другого, вообще говоря, не существовало бы. О чём теорию то строить, если изначальных данных из практики мы не получали?
Главное запомните — подгонка решения под ответ это не просто нормально, а хорошо и естественно. За такое Нобеля дают. Эйнштейн не предсказал фотоэффект, он его объяснил. А вот за своё предсказание различных эффектов связанных с ограниченностью скорости света Нобеля он не получал, хотя да — тут было именно что предсказание. Да и если посмотреть списки премий по научным дисциплинам, то очень многие идут с формулировкой «За объяснение…» «За вклад в понимание…».
Итак, раз идей о том, как вывести формулу, нет — будем моделировать.
Моделировать будем в среде Wolfram Mathematica. Mathematica очень проста в использовании, быстра, приятный и интуитивно понятный интерфейс (ну разве что Ctrl+Enter нужно знать — это комбинация для запуска выполнения куска кода на котором мы стоим; главная и основная) и главное там шикарный хелп который на 90% процентов состоит из примеров + куча ссылок по теме. Действительно полезные ссылки в самом хелпе, так что я порой начинаю там залипвнув сёрфить как в инете. Очень легко и просто отображать данные — строить графики, таблицы какие угодно и как угодно, наверно, на все случаи жизни, что для презентаций порой просто неоценимо. Устанавливайте и пробуйте — залипните и не пожалеете.
Кстати все картинки этой статьи были сделаны в Wolfram Mathematica.
Вот код для моделирования сбора коллекции из 40 элементов. В коде достаточно много комментариев. Сам алгоритм написан так, чтобы быть максимально понятным при прочтении, но при этом, правда, потерял в скорости. У меня при 100 тыс. итераций работает минут 10.
(*Медленный но понятный алгоритм*)
SeedRandom[1234];(*"фиксирует"рандом. Когда мы хотим полуить случайную последовательность, то можем каждый раз получать новую, а можем каждый раз получать ту же самую.Если СидРандом задан, то последовательность будет всегда генериться одна и таже.*)
NPosibleElems=40;(*Количество уникальных элементов в коллекции*)
WhatWeHave=Table[0,{i,1,NPosibleElems}];(*То что мы имеем. Массив всегда должен быть длинной равной "Количество уникальных элементов". то что имеем обозначем 1, то что не имеем обозначаем 0. Если захотим смоделировать ситуацию когда уже часть предметов есть, то нужно будет просто сделать этот массив не нулевым*)
WhatWeWantToHave=Table[1,{i,1,NPosibleElems}];(*То что мы хотим получить. Массив всегда должен быть длинной равной "Количество уникальных элементов". а то что нужно обозначем 1, то что не обязательно обозначаем 0. Если захотим смоделировать ситуацию когда целью будет собрать не все предметы, а только какую-то часть, то нужно будет сделать этот массив не весь из единиц*)
TargetArray=BitOr[WhatWeHave,WhatWeWantToHave];(*Если мы в желаемом забыли указать то что уже есть, то в силу того что невозможно потерять то что уже было, мы бинарно сложим желаемое с тем что есть. В результате мы получим непротиворечивую цель. Тут ничего править не нужно, это просто для корректной работы программы*)
NumItearations=100000;(*Сколько раз будем проводить испытания. Если вычисления проходят медленно - сделайте кол-во интераций меньше.*)
FinishedSteps=Table[0,{i,1,NumItearations}];(*Массив с результатами, в нём будут содержаться количество полученных элементов к моменту достижения цели. "сколько купили жвачек" прежде чем собрали коллекцию.*)
ProgressIndicator[Dynamic[indic],{1,NumItearations}](*В этом примере мы будем использовать индикатор прогресса. Не проверял её особо на скорость, но вроде не сильно тормозит. Переменная indic в данном случае динамическая. Тоесть изменяя её гдето в одном месте, её изменения отразятся СРАЗУ ЖЕ и в других частях документа. К НАШЕМУ АЛГОРИТМУ ЭТО НЕ ИМЕЕТ ОТНОШЕНИЯ - просто для красоты визуализации. Если не понятно, просто пропустите.*)
For[j=1,j<=NumItearations,j++, (*Начинаем в цикле собирать коллекции.*)
indic=j;(*Обновляем полоску индикатора... точнее переменную которая отвечает за положение полоски, а так как она динамическая, то индикатор сам перерисуется. При желании можно в конец цикла воткнуть, а не тут в начале*)
FindedElems=WhatWeHave;(*FindedElems - временный массив. Нашат "текущая" коллекция. При каждой новой итерации мы её будем снова сбрасывать в дфолт*)
While[ Total[TargetArray-FindedElems]!=0,(*Цикл сбора коллекции. Будем открывать новые жвачки до тех пор пока коллекцию не соберём. По идее его не плохо было бы всё же ограничить разумным числом, а то есть какаято мизерная вероятность что и за сто тысяч милионов жвачек мы коллекцию не соберём - в итоге комп может конкретно тут подвиснуть.*)
NewItem=RandomInteger[{1,NPosibleElems}];(*Эмулятор новой жвачки, собственно получение рандомного номера вкладыша*)
If[FindedElems[[NewItem]]!=1,FindedElems[[NewItem]]=1];(*Если не было такого вкладыша - добавляем его в коллекцию*)
FinishedSteps[[j]]+=1;(*Подсчитываем сколько вкладышей мы получили*)
];
];
(*Рисуем гистограмму (с настройками построения гистограммы по умолчанию). Также вытаскиваем данные из полученной гистограммы*)
{bins,count}=HistogramList[FinishedSteps];
HistoList=Transpose[{binsN[[2;;]],count}];
TickL=20;
Show[{Histogram[FinishedSteps],ListPlot[HistoList,PlotStyle->{Darker[Red],PointSize[Large]}]},Ticks->{Table[i,{i,0,Last[bins],TickL}],Automatic}]
(*Рисуем граффик вероятностей*)
ProbList=Transpose[{bins[[2 ;;]],count/NumItearations}];
ListLinePlot[ProbList]
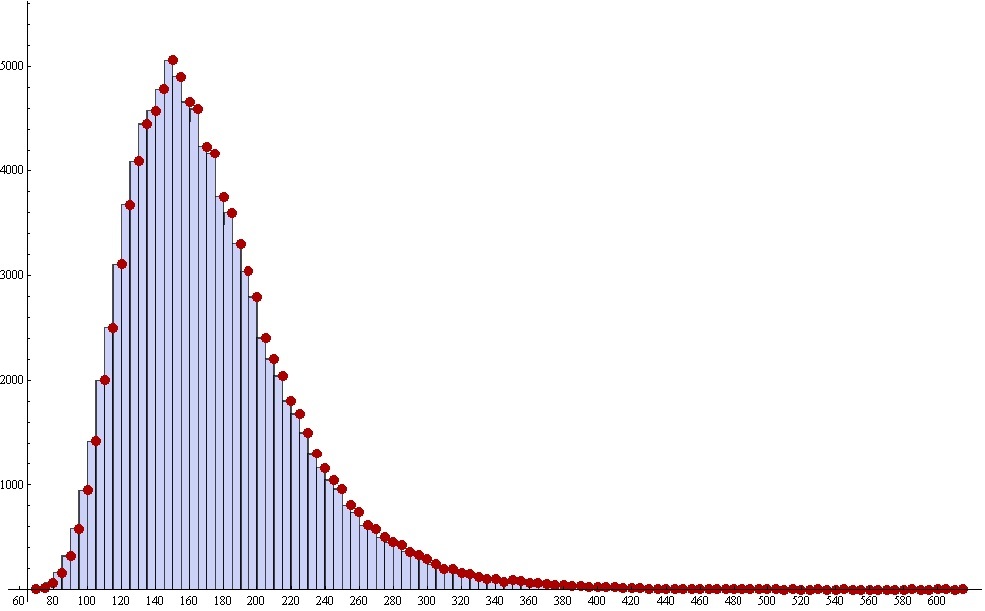
В результате получаем вот такую картинку. Это гистограмма. В ней каждый столбец имеет свою координату на горизонтальной оси, свою высоту и ширину. Высота столбца обозначает, сколько раз из 100000 тысяч итераций коллекция была закончена за n шагов, причём n в данном случае это и есть координата на горизонтальной оси. Грубо, но в целом верно. А если точнее, то нужно вспомнить про ширину столбца, он тут не просто так. Дело в том, что при построении гистограммы, выбор «адекватной» ширины столбцов является вопросом архиважным и архисложным. Когда же его выбрали, и показали вам готовый результат, то вы должны помнить, что на самом деле, высота столбца обозначает, сколько раз произошли события, которые имеют координату больше левой границы и меньше правой границы столбца. Предположим, что у нас в принципе возможны только целые числа, а ширину столбцов мы по глупости сделаем 0.25. В итоге мы вместо «гладкой» картинки получим «расчёску» из столбцов, как забор с дырками — то есть столбец, то нет, то есть, то нет. Если же мы ширину возьмём очень большой, то можем получить просто один очень широкий столбец — толку от него не будет никакого. Все изгибы и нюансы будут просто отсутствовать.
Сейчас высота столбцов обозначает, сколько раз из всех испытаний коллекция была собрана за определённое количество шагов (открытий жвачек). Чтобы узнать вероятность получения коллекции на определённом шаге, мы должны высоту столбцов поделить на общее количество испытаний, и таким образом, получим численно смоделированный ответ к поставленной задаче о коллекции.
Как уже было упомянуто, после случайно встреченной задачки про траекторию (ссылку смотрите выше), возникла идея, которая помогла не только оптимизировать алгоритм, но в конечном итоге вывести формулу.
Любопытная таблица
Каждый момент процесса собирания коллекции можно описать двумя числами: сколько уникальных элементов и сколько повторов. Вероятность получить уникальный элемент коллекции при следующем получении нового элемента (в новой жвачке получить вкладыш которого ещё не было) не зависит от того, какие именно элементы у вас уже есть, а зависит лишь от того, сколько у вас уникальных элементов и сколько всего элементов в коллекции.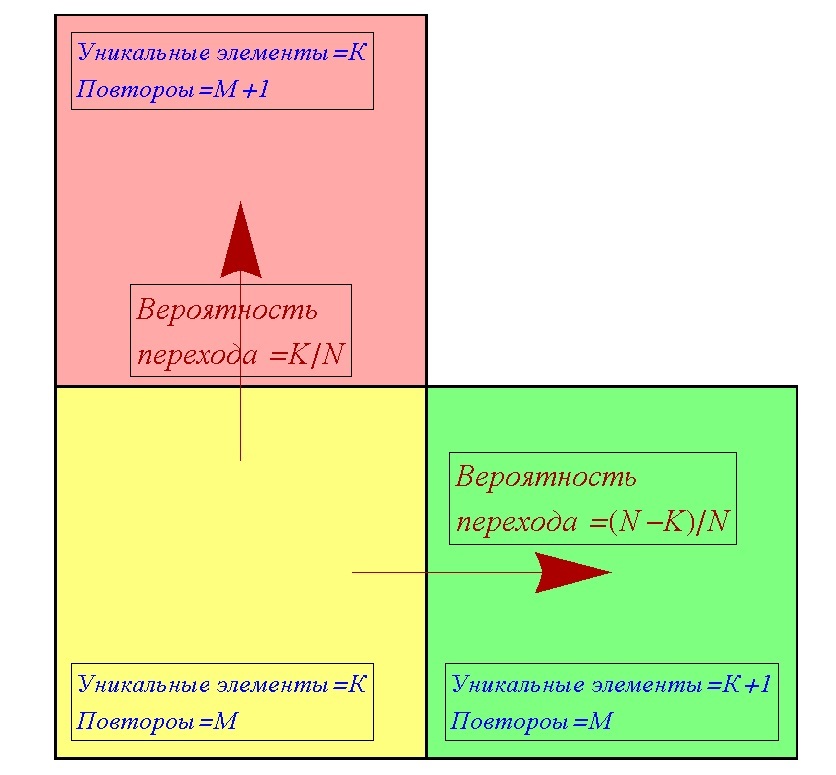
Пусть в какой-то момент есть K уникальных элементов, M повторов, а всего в коллекции N элементов. Стоит уточнить, что под количеством повторов подразумеваются все те элементы, которые останутся у нас, если из всего нашего текущего набора мы уберём ровно по одному уникальному элементу что были. Например, есть 4 яблока, и 3 груши, всего уникальных элементов 2 — это яблоко и груша, а повторов 7 — это 3 яблока и 2 груши. При получении нового элемента, мы можем перейти из текущего состояния (K, M) в одно из двух других состояний. Либо у нас увеличится количество уникальных элементов (K+1, M), либо у нас увеличится количество повторов (K, M+1). Таким образом, мы можем построить таблицу переходов, для любого случая (K, M).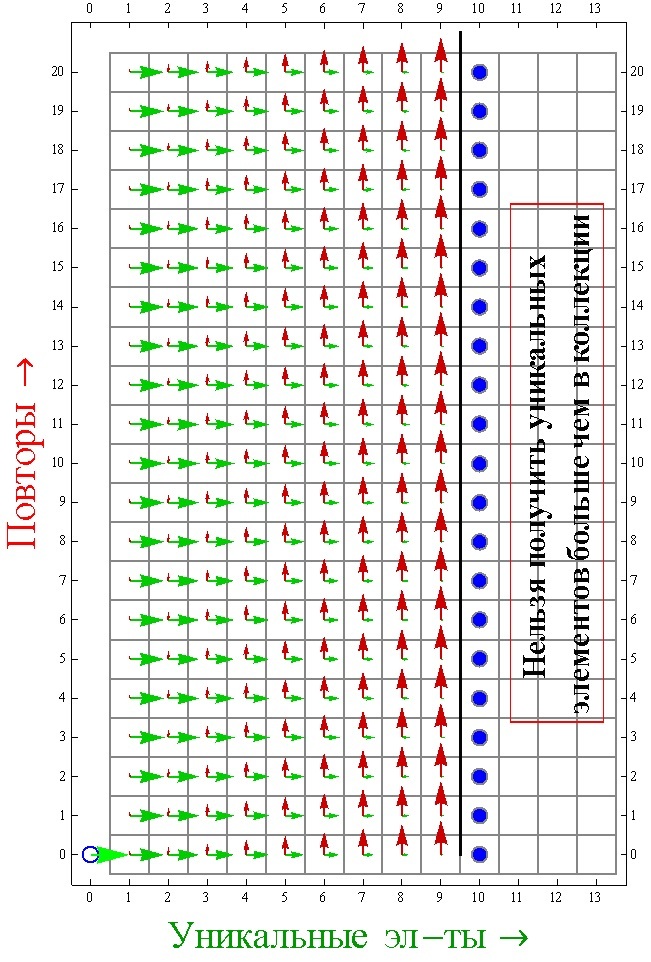
На основе такого подхода, мы можем построить алгоритм для моделирования процесса сбора коллекции. Теперь нам нужно будет на каждом шаге с вероятностью (N –K)/ N переходить либо в клетку (K+1, M) либо c вероятностью K/ N в клетку (K, M+1), до тех пор, пока K
Вот собственно код этого алгоритма. Работает он всё же побыстрее, чем первый вариант.
SeedRandom[1234];(*"фиксирует"рандом. Когда мы хотим полуить случайную последовательность, то можем каждый раз получать новую, а можем каждый раз получать ту же самую.Если СидРандом задан, то последовательность будет всегда генериться одна и таже.*)
NPosibleElems=40;(*Количество уникальных элементов в коллекции*)
NumItearations=100000;(*Сколько раз будем проводить испытания. Если вычисления проходят медленно - сделайте кол-во интераций меньше.*)
Results=Table[0,{i,1,NumItearations}];(*Массив с результатами, в нём будут содержаться количество полученных элементов к моменту достижения цели. "сколько купили жвачек" прежде чем собрали коллекцию.*)
ProgressIndicator[Dynamic[indic],{1,NumItearations}](*В этом примере мы будем использовать индикатор прогресса. Не проверял её особо на скорость, но вроде не сильно тормозит. Переменная indic в данном случае динамическая. Тоесть изменяя её гдето в одном месте, её изменения отразятся СРАЗУ ЖЕ и в других частях документа. К НАШЕМУ АЛГОРИТМУ ЭТО НЕ ИМЕЕТ ОТНОШЕНИЯ - просто для красоты визуализации. Если не понятно, просто пропустите.*)
For[i=1,i<=NumItearations,i++,(*Начинаем в цикле собирать коллекции.*)
indic=i;(*Обновляем полоску индикатора... точнее переменную которая отвечает за положение полоски, а так как она динамическая, то индикатор сам перерисуется*)
n=0;(*Скольо УНИКАЛЬНЫХ элементов коллекции у нас уже есть*)
m=0;(*Сколько ПОВТОРОВ в коллекции у нас есть. Если у нас есть 2 яблока и 3 груши, то уникальных предметов у нас 2 -это {Яблоко, Груша}. А повторов у нас 3 - это одно ЛИШНЕЕ яблоко и две ЛИШНИХ груши.*)
While[n n,n+=1,m+=1];(*С вероятность n/NPosibleElems мы увеличиваеи количество повторов, а с вероятностью 1-n/NPosibleElems увеличиваем кол-во уникальных элементов.*)
];
Results[[i]]=n+m;(*Сумма уникальных и повторых элементов, это общее количество элементов которое у нас есть, или же то кол-во шагов (открытий жвачки) которое было сделано прежде чем колекция была собрана*)
];
(*Дальше также рисуем как в прошлом примере.*)
{bins,count}=HistogramList[Results];
HistoList=Transpose[{binsN[[2;;]],count}];
TickL=20;
Show[{Histogram[Results],ListPlot[HistoList,PlotStyle->{Darker[Red],PointSize[Large]}]},Ticks->{Table[i,{i,0,Last[bins],TickL}],Automatic}]
(*Рисуем граффик вероятностей*)
ProbList=Transpose[{bins[[2 ;;]],count/NumItearations}];
ListLinePlot[ProbList]
Теперь разовьём идею дальше. Можно попробовать посчитать, сколько существует вариантов попасть в клетку с фиксированными (K, M). В клетку (K, M) можно попасть либо из клетки (K, M-1) либо из клетки (K-1, M). Кроме случаев, когда у нас либо только один уникальный элемент, либо нет повторов, то есть K=1, M=0, в них можно попасть только единственным из двух способов. Обозначим количество способов попасть в клетку (K, M) как V[K, M]. Из клетки (K, M-1) в клетку (K, M) можно попасть К различными вариантами, потому что получить ещё один повтор можно таким количеством вариантов, сколько уже есть уникальных элементов. Из другой же соседней клетки (K-1, M) в клетку (K, M) можно попасть (N-(K-1)) количеством вариантов, потому что в клетке (K-1, M) уникальных элементов (K-1), и соответственно недостаёт (N-(K-1)) элементов. Вообще же вариантов попасть в клетку (K, M) через клетку (K, M-1) можно V[K, M-1]*K вариантами, то есть произведение количества вариантов попасть в саму (K, M-1) умноженное на количество вариантов попасть из (K, M-1) в (K, M). Аналогично и с вариантами попасть в клетку (K, M) через клетку (K-1, M) получаем V[K-1, M]* (N-(K-1)). Суммарно же попасть в клетку (K, M) можно попасть V[K, M-1]*K+ V[K-1, M]* (N-(K-1)) количеством вариантов. Таким образом, мы получаем саму полезную для нас формулу о количестве способов попадания в клетку (K, M).
V[K, M]=V[K, M-1]*K+ V[K-1, M]* (N-(K-1))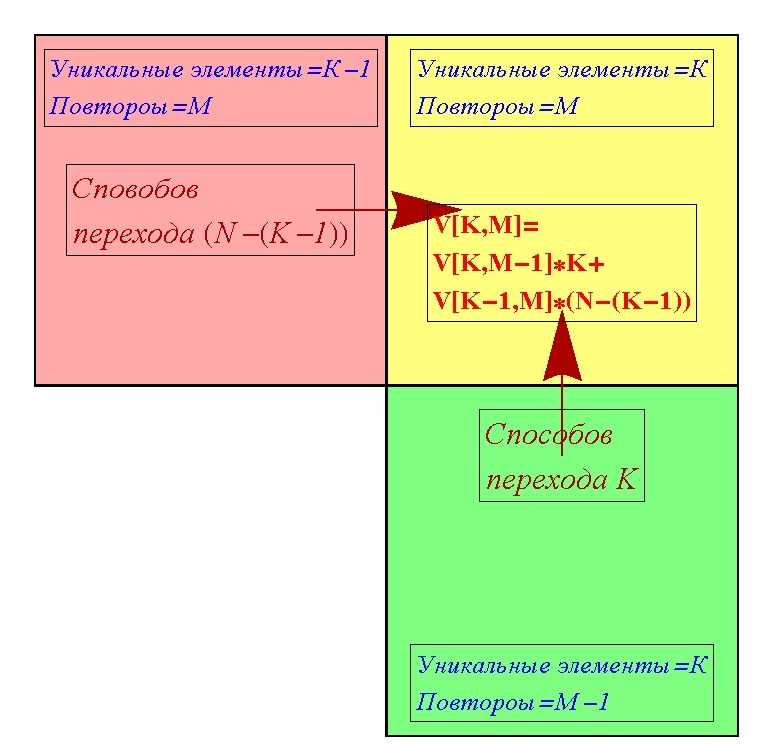
Используя это правило, можно последовательно посчитать количество способов попадания для любой клетки (K, M). То есть это не будет формула которая сразу выдаст значение вариантов для конкретных (K, M), но у нас будет таблица с символьными ответами, а не с численным моделированием. Вот собственно алгоритм.
KKT=10;
MMT=10;
V=Table[0,{k,1,KKT},{m,1,MMT}];
V[[1,1]]=NN;
For[k=2,k<=KKT,k++,V[[k,1]]=FullSimplify[V[[k-1,1]]*(NN-(k-1))]];
For[m=2,m<=MMT,m++,V[[1,m]]=NN];
For[k=2,k<=KKT,k++,
For[m=2,m<=MMT,m++,
V[[k,m]]=V[[k-1,m]]*(NN-(k-1))+V[[k,m-1]]*k;
];
];
MatrixForm[V]
И вот полученная таблица, не смотря на весь свой огромный размер, обладает замечательной особенностью. Все столбцы таблицы пропорциональны с некоторым числовым коэффициентом первому столбцу. И данные числовые коэффициенты не зависят от количества элементов в коллекции. Если разделить все столбцы этой таблицы на первый столбец, то получим вот такой результат.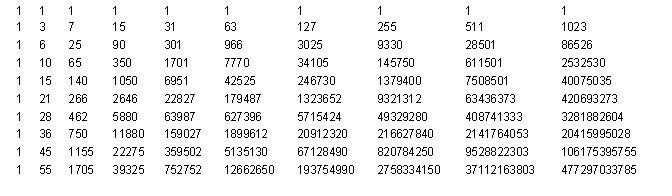
Честно говоря, я был крайне озадачен, когда первый раз это получил. Это казалось настолько красивым и невероятным, что у меня просто в голове не укладывалось. Числа эти не зависят от количества элементов в коллекции и зависят только от количества повторов и уникальных элементов, то есть от (K, M). Если понять, как эти числа получаются, то задача будет полностью решена и сводится к весьма простой формуле. Но что это за числа, я не имел, ни малейшего понятия.
Азъ есмь Alpha Wolfram
Представьте, что во время каких-то вычислений, вы сталкиваетесь с некоторым коэффициентом, например 5.01326. Вы знаете, что получили его не с абсолютной точностью, но подумали, а вдруг это число какое-то «красивое» и выражается через известные математические константы, или является корнем какого-то натурального числа, логорифмом, синусом. Ну, или если и не является, то очень близко к нему. Например, с такой потребностью можно столкнуться при анализе чужого кода, со списком констант, но без комментариев. В таком случае меня выручал сайт Wolfram Alpha.
Вот пример ответа на запрос о числе 5.01326. (я загадал корень из 8*Pi)
Я затрудняюсь назвать Wolfram Alpha поисковиком, он нечто большее. Он не просто ищет на просторах инета страницы, которые как-то относятся к тому, что вы ищите. Он часто вычисляет ответ на ваш вопрос сам. Причём вместо «бонуса» рекламы, как делают обычные поисковики, он выдаёт действительно интересные факты, относящиеся к данному вопросу. Не ссылки, а именно сразу факты на странице. Ссылки, правда, тоже конечно выдаёт в конце страницы, но обычно всё, что он выдаст сам, бывает более чем достаточно.
Так же при желании можно получить доступ к базам данным о погоде, каких-то финансовых данных, географии, биологии, химии и прочем. Например вот. Ссылки уже с готовыми запросами
Графики температуры, давления и прочего в Кабуле с 97ого по 99ый годы.
Информация об акциях компании Apple за последние 16 лет
Карта и информация о территории СССР
Основные свойства оксида азота
Помимо ответов на вопросы типа «что такое….?» он может выдавать решения дифференциальных уравнений введенных ему в строку ввода. Или нарисовать график, который вы попросили. То есть не нужно никаких сторонних программ, плагинов и прочего — можно просто решить дифференциальное уравнение и отрисовать график введя его в строку ввода Wolfram Alpha. Но всё же, отмечу, что всё в пределах разумного — если что-то довольно трудоёмкое, то он откажется считать «на халяву», и для сложных задач и быстродействия всё же потребуется Wolfram Mathematica.
В частности можно делать запрос в виде последовательностей чисел, и помимо основных характеристик, данного массива, он может (не всегда правда) выдать предположительный вариант продолжения последовательности. Именно эта его возможность и была использована для выяснения, что же за числа были получены в клетках выше описанной таблицы.
Математический детектив
Те, кто не любят детективы, эту главу могут пропустить и перейти к следующей.
Я начал с того, что брал строки полученного массива W и просто вводил вручную в Wolfram Alpha. Но можно и не копипастить, а прямо из Wolfram Mathematica напрямую обращаться к Wolfram Alpha без браузеров. Причём сразу запрашивать ту часть информации, которая интересует. Вот код, который в цикле запрашивает предположительную формулу введённой последовательности.
For[i=1,i<=Length[W],i++,
Print[i," ",W[[i]]];
Print[WolframAlpha[ToString[W[[i]]],{{"PossibleSequenceIdentification",1},{"Output"}}]];
Print[""];
];
К сожалению не все запросы были успешно обработаны, причины бывают разными, иногда помогает уменьшить или увеличить размер вводимой последовательности. Но из полученных ответов, после пристального взгляда, можно обнаружить, что последовательности, которые мы вводили, имеют вид a0×0^n+a1×1^n +a2×2^n + a3×3^n +…. Количество слагаемых равно порядковому номеру введённой последовательности. Но коэффициенты an линейно входят в формулу, а значит, их можно легко найти из системы линейных уравнений. Более того если приглядеться, то все слагаемые имеют общий множитель, обратно пропорциональный факториалу номера последовательности, а также, что слагаемые знакопеременные. Поэтому искать слагаемые будем с учётом этих фактов. Систему решаем, разумеется, не вручную, а в Wolfram Mathematica. Вот код для решения.
TempAr = W;
CoefRes = Table[{}, {i, 1, Length[TempAr]}];
For[k = 1, k <= Length[TempAr], k++,
An = Table[a[i], {i, 2, k}];
(*Conds=Table[An[[i]]>0,{i,1,Length[An]}]*)
F[z_] := (Total[
Table[(((-1)^(k + 1))*(-1)^(i + 1))*i^z*An[[i - 1]], {i, 2,
k}]] + (-1)^(k + 1))/((k - 1)!);
Eqs = Table[F[i] == TempAr[[k]][[i]], {i, 1, Length[An]}];
Res = Solve[Eqs, An];
CoefRes[[k]] = Prepend[(An /. Res)[[1]], 1];
ue = Table[(-1)^k*(-1)^i, {i, 1, Length[CoefRes[[k]]]}];
CoefRes[[k]] = CoefRes[[k]]*ue;
];
CoefRes // Column
Коэффициенты нашли, но они тоже, не то что бы простые. Повторяем с ними ту же самую процедуру попытки поиска формулы для них. И тут нас ждёт разочарование — Wolfram Alpha в режиме халявы не может распознать эти последовательности. Ну что же — пробуем сами.
Попробуем разложить все эти числа на простые множители и немного помедитируем, созерцая полученное. Такой подход часто бывает полезен, для того чтобы распознать формулу последовательности.
For[i=1,i<=Length[W],i++,
Print[FactorInteger[Abs[CoefRes[[i]]]]//Column];
]
Присмотревшись к полученным разложениям, видно, что каждое из чисел в последовательностях делится на свой порядковый номер в определённой степени, причём эта степень растёт с ростом номера последовательности. Присмотревшись ещё внимательнее видно, эта степень равна номеру последовательности минус 2. Ну, хорошо, разделим тогда все числа в наших последовательностях на их порядковые номера в степени номера последовательности минус 2.
CoefRes2=CoefRes;
For[i=1,i<=Length[CoefRes],i++,
For[j=1,j<=Length[CoefRes[[i]]],j++,
CoefRes2[[i]][[j]]=Abs[CoefRes[[i]][[j]]]/j^(i-2);
];
]
CoefRes2
© Habrahabr.ru
