Хаос внутри судоку
 Многие из вас наверняка знакомы с такой головоломкой, как судоку. Возможно, даже реализовывали программу для автоматического решения. На хабре тема судоку обсуждалась уже множество раз, и, как показывает практика, практически любой способ автоматического нахождения ответа в итоге сводится к направленному перебору. И это вполне естественно, ведь даже ручные решения придерживаются тех же принципов. Но что, если поступить иначе?
Многие из вас наверняка знакомы с такой головоломкой, как судоку. Возможно, даже реализовывали программу для автоматического решения. На хабре тема судоку обсуждалась уже множество раз, и, как показывает практика, практически любой способ автоматического нахождения ответа в итоге сводится к направленному перебору. И это вполне естественно, ведь даже ручные решения придерживаются тех же принципов. Но что, если поступить иначе?
В данной статье я рассмотрю один очень занятный метод, предложенный в 2012 году, основанный на строго математическом подходе. Программная реализация прилагается.
Этап 0. Формулировка задачи
В первую очередь вспомним описание головоломки. Задачей любой раскладки судоку является заполнение поля 9×9 цифрами от 1 до 9 так, чтобы ни одни строка, столбец или выделенный блок 3×3 не содержали одинаковых цифр (блоки выделены жирными границами на картинке). Так же обычно подразумевается единственность такого заполнения, данный факт помогает в решении задач высокого уровня сложности. Нам же (как и алгоритмам с перебором) предположение о единственности решения не требуется. При этом стоит оговориться: описанный метод позволяет найти первое попавшееся решение. Перечисление же всех решений данным методом невозможно (ну или как минимум непрактично).
Этап 1. Формализация задачи
Опишем математически, что такое корректно заполненное поле. У нас есть сетка размером 9×9, в каждой клетке может располагаться только одно число от 1 до 9. Было бы разумным ввести 81 целочисленную переменную, но вместо этого мы будем оперировать булевыми значениями. Это позволит использовать формальный логический подход.
Введём множество 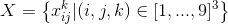 логических переменных, наделив их следующим смыслом:
логических переменных, наделив их следующим смыслом: 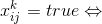 в клетке
в клетке 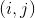 записано число
записано число 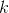 . Определение корректного поля в судоку диктует нам ряд ограничений, которые мы введём на множестве наших переменных.
. Определение корректного поля в судоку диктует нам ряд ограничений, которые мы введём на множестве наших переменных.
Для простоты сперва введём q-местный предикат 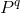 , истинный только в том случае, если ровно один из его параметров истинен. Вот его формальное описание:
, истинный только в том случае, если ровно один из его параметров истинен. Вот его формальное описание:
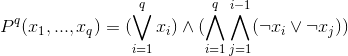
С его помощью запишем 4 вида ограничений, описанных нами ранее:
- в каждой клетке может находиться только одно из 9 чисел:
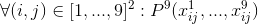
- в каждой строке каждое число встречается ровно 1 раз:
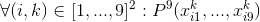
- в каждом столбце каждое число встречается ровно 1 раз:
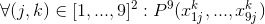
- наиболее неприятный для описания случай — каждый из 9 блоков 3×3 содержит каждое число ровно 1 раз:
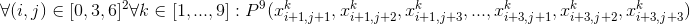
Если объединить все приведённые формулы, избавившись от кванторов, мы получим вот это:
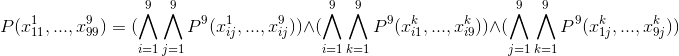
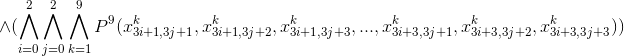
Данная формула имеет Конъюнктивную Нормальную Форму (поскольку предикат 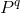 тоже записан в КНФ), что является весьма удобным способом для программной обработки.
тоже записан в КНФ), что является весьма удобным способом для программной обработки.
У нас на руках есть общая формула, которая описывает все возможные поля судоку. На практике же в поле судоку есть несколько подсказок. Если в клетке 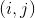 стоит число
стоит число 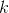 , то мы знаем, что
, то мы знаем, что 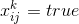 . Помимо этого мы можем легко определить множество переменных, которые в этих условиях обязаны быть ложными. Подставим все эти величины и упростим каждый из дизъюнктов. Далее мы вправе удалить из формулы повторяющиеся дизъюнкты (если они появились) и заявить, что полученная функция (всё ещё в КНФ) полностью определяет наш расклад, а каждое решение уравнения
. Помимо этого мы можем легко определить множество переменных, которые в этих условиях обязаны быть ложными. Подставим все эти величины и упростим каждый из дизъюнктов. Далее мы вправе удалить из формулы повторяющиеся дизъюнкты (если они появились) и заявить, что полученная функция (всё ещё в КНФ) полностью определяет наш расклад, а каждое решение уравнения 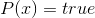 даёт нам уникальное решение исходной задачи. Так что, по большому счёту, мы свели судоку к классической задаче выполнимости из математической логики. Она является NP-полной, что в какой-то степени объясняет нам сложность исходной головоломки.
даёт нам уникальное решение исходной задачи. Так что, по большому счёту, мы свели судоку к классической задаче выполнимости из математической логики. Она является NP-полной, что в какой-то степени объясняет нам сложность исходной головоломки.
Не совсем верно говорить, что мы свели судоку к задаче выполнимости, ведь в ней цель выяснить, может ли формула быть истиной на каком-то наборе аргументов. Для судоку же нам заранее известно, что формула является выполнимой.
Просто дело в том, что часто под задачей выполнимости понимают именно поиск аргументов, на который формула становится истинной.
Этап 2. Немного математического анализа
С этого момента можно забыть, что мы решаем судоку, поскольку описанный метод подходит для любой задачи выполнимости. И нам для его описания понадобится несколько новых обозначений.
Предположим, что есть формула, состоящая из N логических переменных 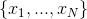 и M дизъюнктов. Введём матрицу
и M дизъюнктов. Введём матрицу 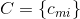 размера MxN, такую, что:
размера MxN, такую, что:
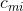 =1, если m-й дизъюнкт содержит
=1, если m-й дизъюнкт содержит 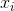 ;
; 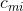 =-1, если m-й дизъюнкт содержит отрицание
=-1, если m-й дизъюнкт содержит отрицание 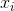 ;
; 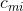 =0, если m-й дизъюнкт не содержит
=0, если m-й дизъюнкт не содержит 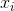 .
.
Далее введём вектор 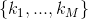 такой, что
такой, что 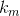 = {количество переменных в дизъюнкте с номером m}.
= {количество переменных в дизъюнкте с номером m}.
И, в конце концов, каждому 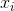 поставим в соответствие вещественное число
поставим в соответствие вещественное число 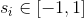 .
. 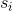 это непрерывная величина, которая для
это непрерывная величина, которая для 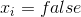 равна -1, а для
равна -1, а для 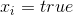 равна 1. В каком-то смысле
равна 1. В каком-то смысле 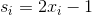 .
.
Теперь можно разобраться, зачем всё это нужно. Каждому из M дизъюнктов поставим в соответствие функцию 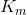 , определённую следующим образом:
, определённую следующим образом:
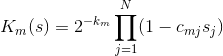
Эти функции хороши тем, что обращаются в 0 (если один из множителей равен нулю) 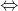 соответствующий им дизъюнкт с соответствующими значениями
соответствующий им дизъюнкт с соответствующими значениями 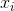 является истинным. Более того, добавление множителей с
является истинным. Более того, добавление множителей с 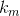 гарантирует, что каждая из функций принимает значения из отрезка
гарантирует, что каждая из функций принимает значения из отрезка 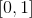 в области своего определения. Но интереснее будет сумма их квадратов:
в области своего определения. Но интереснее будет сумма их квадратов:
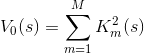
Эта сумма примечательна тем, что обращается в нуль исключительно на тех векторах s, которые соответствуют решениям изначального уравнения на 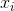 . И все эти нули являются локальными минимумами нашей функции (в силу области значений).
. И все эти нули являются локальными минимумами нашей функции (в силу области значений).
Этап 3. Система дифференциальных уравнений
Уравнение, несмотря на кажущуюся простоту записи, по факту оказывается весьма неприятным. Это полином большой степени от очень большого числа аргументов. Можно даже не пытаться искать его минимум аналитически.
Давайте сделаем несколько добавлений:
- представим каждый
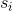 как функцию
как функцию 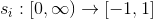 ;
; - введём ещё ряд функций
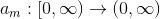 ;
; - вместо нашей
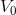 будем рассматривать
будем рассматривать 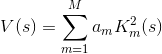
Так как все 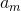 строго положительные, то наше уравнение своих самых важных свойств не теряет.
строго положительные, то наше уравнение своих самых важных свойств не теряет.
При этом 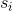 и
и 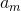 мы будем находить из следующих условий:
мы будем находить из следующих условий:
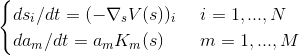
∇ в этой записи — оператор градиента.
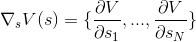
Первое уравнение явно намекает нам на метод сопряжённых градиентов для поиска экстремумов.
Со вторым немного хитрее, его я оставлю на совести авторов. Если вкратце — оно нужно для того, чтобы система быстрее сходилась к решению. Я сам не проверял, является ли это правдой.
Уравнение на 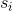 можно переписать в явном виде, продифференцировав V:
можно переписать в явном виде, продифференцировав V:

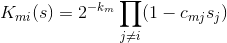
Начальные условия в точке 0 берутся произвольными. Ну, а решение мы в итоге получаем по такой формуле: 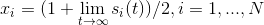
Высказывание о произвольности начальных условий, вообще говоря, ложно. Авторы метода утверждают, что на множестве начальных условий нулевой меры ответ найти не получится. Но, поскольку множество «маленькое», на практике его можно игнорировать.
Этап 4. Наконец-то численное решение
Одним из самый простых и удобных способов решать системы обыкновенных дифференциальных уравнений является метод Рунге-Кутты. Нами будет использован вариант метода, носящий фамилии Кэша-Карпа. Сейчас я коротко о нём расскажу.
Итак, пусть у нас есть уравнение 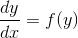 . x в списке параметров мы опускаем, поскольку в наших уравнениях значения производных
. x в списке параметров мы опускаем, поскольку в наших уравнениях значения производных 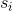 и
и 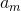 не зависят явно от t. Нам же проще.
не зависят явно от t. Нам же проще.
Считаем, что задано начальное условие  , а требуется нам найти значение
, а требуется нам найти значение 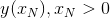 .
.
Для поиска ответа мы построим последовательность 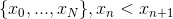 и будем вычислять значения
и будем вычислять значения 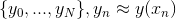 .
.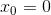 и
и 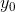 нам известны, считаем их базой индукции. Далее, пусть мы находимся на шаге n
нам известны, считаем их базой индукции. Далее, пусть мы находимся на шаге n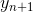 , исходя из следующей формулы:
, исходя из следующей формулы: 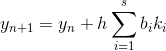 , в которой последовательность
, в которой последовательность 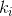 находится как:
находится как: 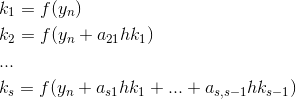
Числа  ,
, 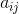 и
и 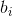 являются фиксированными константами, от которых сильно зависит точность метода (в каноничном методе есть ещё константы
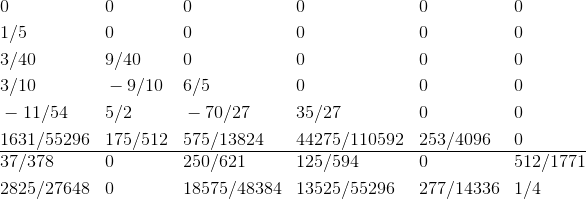
являются фиксированными константами, от которых сильно зависит точность метода (в каноничном методе есть ещё константы 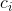 , но в нашем случае они попросту не нужны).
, но в нашем случае они попросту не нужны).
Вместе набор этих коэффициентов называется «таблицей Бутчера»:

Для метода Кэша-Карпа у нас есть такая таблица:
Здесь у нас два вектора b. Если использовать первый из них, то на каждом шаге ошибка вычисления оценивается как  . А если взять второй вектор b, то оценка погрешности будет
. А если взять второй вектор b, то оценка погрешности будет 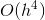 . Посчитав менее точное значение
. Посчитав менее точное значение 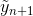 , мы можем эвристически оценить абсолютную ошибку на шаге как
, мы можем эвристически оценить абсолютную ошибку на шаге как 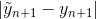 (разница решений 4-го и 5-го порядков). И в случае, если ошибка нас не устраивает, мы можем заменить текущий шаг h на другое значение и пересчитать текущую итерацию. В частности, возможно 2 варианта:
(разница решений 4-го и 5-го порядков). И в случае, если ошибка нас не устраивает, мы можем заменить текущий шаг h на другое значение и пересчитать текущую итерацию. В частности, возможно 2 варианта:
- слишком большая ошибка — уменьшаем шаг, запускаем итерацию с начала;
- слишком маленькая ошибка — увеличиваем шаг, запускаем следующую итерацию (тем самым уменьшаем суммарное время вычислений).
Остановить же процесс поиска можно тогда, когда все вычисленные 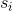 по модулю станут мало отличаться от единицы (разницы в 0.1 вполне достаточно).
по модулю станут мало отличаться от единицы (разницы в 0.1 вполне достаточно).
Эпилог
Что ж, определённо многовато возни для столь простой задачи. Лично я во всём этом материале постарался разобраться исключительно из любопытства, так как нечасто встречаю столь широкое применение математики в столь неожиданных местах.
Работает ли всё выше описанное на практике? Авторы кодом не поделились, так что мне пришлось написать свой.
Задачу он решает, но для судоку из класса «самых сложных в мире» работает весьма медленно, и длительность решения сильно зависит от начальных данных (то есть от рандома). Я не могу с уверенностью ответить, проблема ли это метода или моей реализации. Явных багов замечено не было.
Если вас действительно заинтересовала эта тема, то настоятельно советую почитать оригинал. Я затронул не весь материал, рассматриваемый авторами метода. И спасибо, что дочитали до конца!
Ссылки:
- оригинальная публикация на тему решения судоку
- общий метод решения задачи выполнимости
- метод Кэша-Карпа
- моя реализация на гитхабе (Java)
