Градиентный спуск по косточкам22.10.2019 00:18

В интернете есть много статей с описанием алгоритма градиентного спуска. Здесь будет еще одна.

8 июля 1958 года The New York Times писала: «Психолог показывает эмбрион компьютера, разработанного, чтобы читать и становиться мудрее. Разработанный ВМФ… стоивший 2 миллиона долларов компьютер »704», обучился различать левое и правое после пятидесяти попыток… По утверждению ВМФ, они используют этот принцип, чтобы построить первую мыслящую машину класса «Перцептрон», которая сможет читать и писать; разработку планируется завершить через год, с общей стоимостью $100 000… Ученые предсказывают, что позже Перцептроны смогут распознавать людей и называть их по имени, мгновенно переводить устную и письменную речь с одного языка на другой. Мистер Розенблатт сказал, что в принципе возможно построить «мозги», которые смогут воспроизводить самих себя на конвейере и которые будут осознавать свое собственное существование» (цитата и перевод из книги С. Николенко, «Глубокое обучение, погружение в мир нейронный сетей»).

Ах уж эти журналисты, умеют заинтриговать. Очень интересно разобраться, что на самом деле представляет из себя мыслящая машина класса «Перцептрон».


Двоичная (бинарная) классификация объектов, искусственный нейрон класса «Перцептрон»

Вот наш искусственный нейрон, он делит объекты на два класса (выполняет двоичную классификацию объектов):

image

Итак, у нас есть:

Классификация — потому, что нейрон назначает объекту класс, бинарная (двоичная) — потому, что возможных классов всего два.

$\hat{y}$ [игрик с крышкой] — будем обозначать предсказанное (вычисленное) значение класса для объекта $x$
$y$ [обычный игрик без крышки] — истинные (известные) значения класса для объекта $x$ из обучающей выборки.

Значения $x$ (здесь и дальше $x$ и $w$ — это не единичные значения, а векторы) меняются от объекта к объекту, весовые коэффициенты $w$ (будучи выбраны один раз) остаются неизменны. Для обучающей выборки для каждого объекта $x$ известна метка класса $y$. На этапе обучения нужно подобрать весовые коэффициенты $w$ так, чтобы модель выдавала правильное значение $\hat{y}$ (совпадающие с $y$) для максимального количество объектов обучающей выборки. Предположение о полезности обученного таким образом нейрона базируется на надежде на то, что с подобранными коэффициентами он будет выдавать правильные значение $\hat{y}$ для новых объектов $x$, истинное значение класса $y$ для которых заранее не известно.

Интуитивный смысл взвешенной суммы входов нейрона заключается в том, что все признаки объекта (каждый из признаков — это один из входов нейрона) оказывают влияние на результат классификации объекта, но не все признаки — в одинаковой степени. В какой именно степени — определяют веса; обнуление какого-то весового коэффициента обнуляет вклад соответствующего признака в общую сумму, т.е. это равносильно удалению у объекта признака.


Адаптивный линейный нейрон ADALINE

Нейрон ADALINE (adaptive linear neuron) — это обычный искусственный нейрон вот с такой функцией активации:

$Φ(x,w)=Φ(SUM)=SUM$

$\Phi (x^{(i)},w)=\Phi (\sum _{j=1}^{m}w_{j}x_{j}^{(i)})=\sum _{j=1}^{m}w_{j}x_{j}^{(i)}$

Здесь и дальше верхний индекс $i$ в скобках будет обозначать $i$-й элемент обучающей выборки $x^{(i)}$ или истинное значение класса $y^{(i)}$ или предсказанное значение класса $\hat{y}^{(i)}$ для него же.

Можно сказать, что у такого нейрона функции активации просто нет и на вход квантизатора (порога) подается значение взвешенной суммы входов. Но для единообразия будет удобнее считать, что в качестве активации берется значение взвешенной суммы.

Порог (квантизатор) — предсказывает метку класса:

$ \hat{y}^{(i)}=\left\{\begin{matrix}1,\Phi (x^{(i)},w)\ge \theta \\-1,\Phi (x^{(i)},w)<\theta \end{matrix}\right. $

Если значение активации больше некоторого значения порога θ [тета], то квантизатор назначает объекту метку »1», если значение активации меньше порога θ, то объект получает метку »-1».

Здесь мы можем сформулировать задачу в первом приближении: нам нужно подобрать параметры нейрона


  • весовые коэффициенты $w_j, j=1,..,m$
  • и порог θ [тета]

так, чтобы значения классов $\hat y$, которые нейрон назначает объектам обучающей выборки, совпадали с истинными значениями классов $y$ для этих же элементов (или, по крайней мере, давали правильное значение для большинства).

Немного преобразуем пороговую функцию, возьмем случай для класса $\hat y = 1$ и перенесем порог в левую часть неравенства:

$\begin{gathered} \Phi (x^{(i)},w)\ge \theta \hfill \\\sum _{j=1}^{m}w_{j}x_{j}^{(i)}\ge \theta \hfill \\-\theta +\sum _{j=1}^{m}w_{j}x_{j}^{(i)}\ge 0\hfill \\ \end{gathered}$

обозначим $w_{0}=-\theta$ и $x_{0}=1$

$\begin{gathered} w_{0}x_{0}^{(i)}+\sum _{j=1}^{m}w_{j}x_{j}^{(i)}\ge 0,w_{0}=-\theta ,x_{0}=1\hfill \\\sum _{j=0}^{m}w_{j}x_{j}^{(i)}\ge 0,x_{0}=1\hfill \end{gathered}$

Как видим, нам удалось избавиться от отдельного параметра θ, внеся его под видом нового весового коэффициента $w_0$ под знак суммы, добавив при этом к описанию объекта новый фиктивный единичный признак $x_0=1$.

Скорректируем формулировку задачи с учетом новых обозначений.

Задача': подобрать параметры нейрона — весовые коэффициенты $w_j, j=0,..,m$,
$x_0 = 1$ (признак-константа) — фиктивный нейрон (нейрон смещения)

Начиная с этого места нумеруем признаки и весовые коэффициенты c 0, а не с 1. Про вектор $w$ будем говорить, как про (m+1)-мерный, а не m-мерный. Вектор $x$ в зависимости от контекста можем считать (m+1)-мерным (по большей части в формулах), но при этом помнить, что на самом деле он m-мерный.

Почему нейрон (в нашем случае, правда, это не нейрон, а признак объекта или просто вход, но в случае многослойной сети он превращается в нейрон и обычно его именно так называют) фиктивный — понятно уже сейчас. Почему он еще и смещения станет понятно позднее.

Активация с суммой будут выглядеть теперь так:

$ \Phi (x^{(i)},w)=\Phi (\sum _{j=0}^{m}w_{j}x_{j}^{(i)})=\sum _{j=0}^{m}w_{j}x_{j}^{(i)},x_{0}^{(i)}=1\forall i $

Порог теперь всегда 0 (ноль) (реальное значение переехало в параметр $w_0$):

$ \hat{y}^{(i)}=\left\{\begin{matrix}1,\Phi (x^{(i)},w)\ge 0\\-1,\Phi (x^{(i)},w)<0\end{matrix}\right. $

Еще раз сформулируем задачу другими словами (геометрический смысл задачи)

Если мы внимательно посмотрим на формулу функции активации, то мы увидим, что она представляется собой параметрическую гиперплоскость в (m+1)-мерном пространстве, при этом в первых m измерениях она сосуществует вместе с точками элементов выборки, а (m+1)-е измерение — пространство значений функции, отдельное от элементов.

Теперь, если мы приравняем значение активации к нулю (значение порога), то это тоже будет гиперплоскость, только уже в m-мерном пространстве, т.е. полностью в пространстве значений элементов $x$. Эта гиперплоскость будет разделять элементы $x$ на две непересекающиеся группы.

Обычно в этом месте говорят, что наша задача — подобрать значения параметров $w$, т.е. построить m-мерную гиперплоскость в пространстве элементов так, чтобы элементы обучающей выборки с истинным значением класса »1» оказались по одну сторону плоскости, а элементы с истинным классом »-1» — по другую.

Для тех, кто не совсем понял, что здесь написано, читайте дальше — сейчас мы все увидим, это во-первых. Во-вторых, мы так же увидим, что такая постановка задачи хотя и справедлива, но не совсем полна.


Одномерное пространство (m=1)

Здесь начнет появляться код. Все графики строим с обычной библиотекой Matplotlib, но здесь я еще использую библиотеку Seaborn в одной строчке для настройки области графика, т.к. мне нравится, как у нее это получается, но в принципе можно обойтись и без нее.

# coding=utf-8

import matplotlib.pyplot as plt
import seaborn as sns

# симпатичная сетка на белом фоне
# (без нее русские подписи -> кракозябры)
sns.set(style='whitegrid', font_scale=1.8)
#sns.set(style='whitegrid')

# не будет работать, если включен seaborn
#plt.rcParams.update({'font.size': 16})

Берем множество 1-мерных точек и ответов к ним: 

import numpy as np
import math

# точки - признаки (одно измерение)
X1 = np.array([1, 2, 6, 8, 10])
# метки классов (правильные ответы)
y = np.array([-1, -1, 1, 1, 1])

Здесь у нас каждый i-й элемент массива X1 — это i-й элемент (i-я точка) обучающей выборки (еще точнее — его 1-й и единственный признак): $x^{(i)}=(X1[i])$, $x^{(i)}_1=X1[i]$

Каждый i-й элемент массива y — правильный ответ, истинная метка, соответствующая i-му элементу обучающей выборки с единственным признаком X1[i].

Возьмем всего 5 точек, первые две отнесем к классу »-1», остальные три — к классу »1».

Нарисуем эти точки на линии: 

# ось Ф=0
plt.plot(X1, np.zeros(len(X1)), color='black', lw=2)

# обучающие точки на оси Ф=0
plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300,
        label=u'объект x (1 признак): класс-1 (y=1)')
plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300,
        label=u'объект x (1 признак): класс-2 (y=-1)')

plt.xlabel(u'X1 (единственный признак)')
plt.ylabel(u'Ф (активация)')

plt.legend(loc='upper left')
plt.show()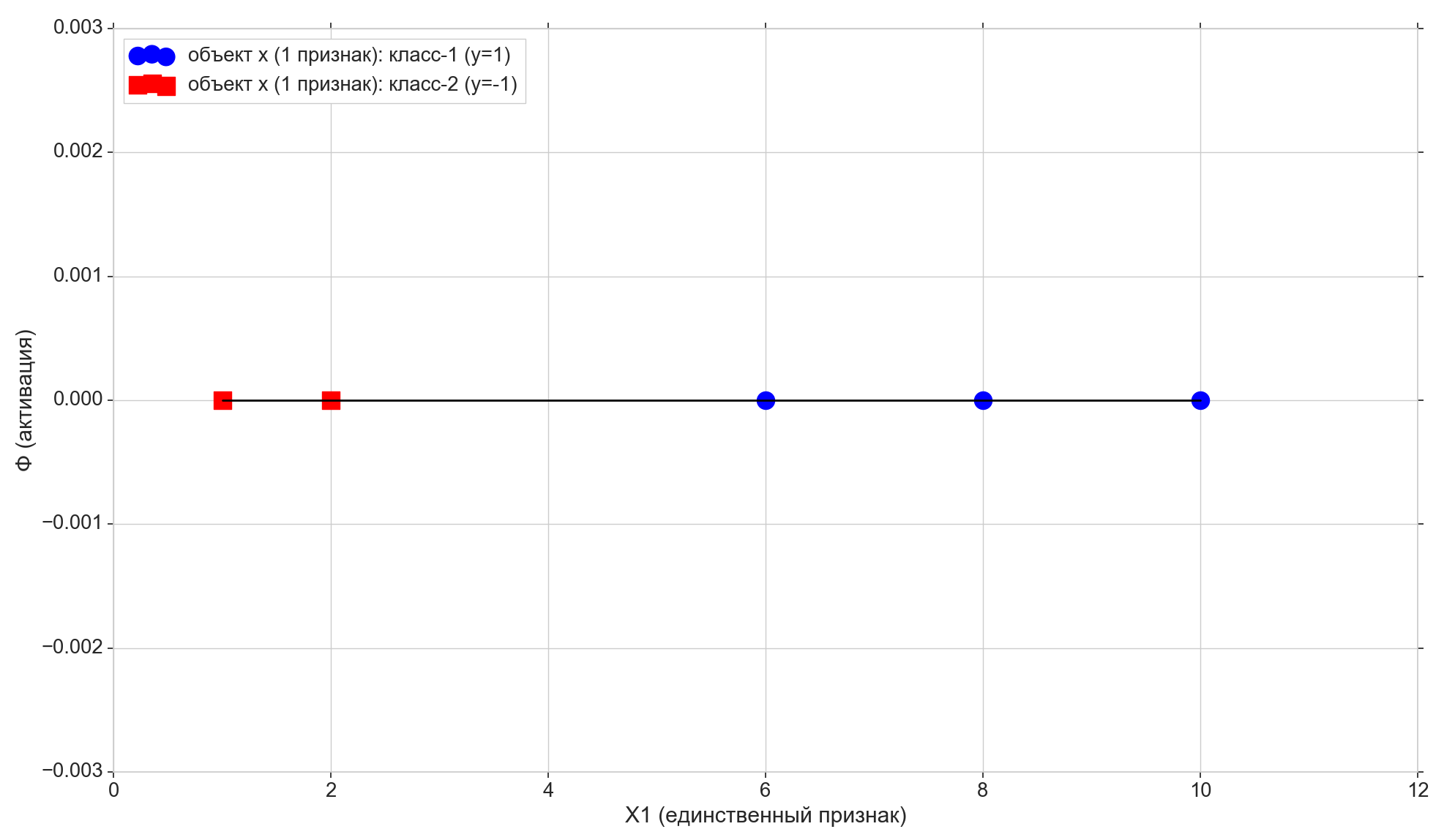


_5ktmhtxmfntpgt0xojlnq_j05e.png

Теперь посмотрим на функцию активации:

$\Phi =w_{0}+w_{1}x_{1}$

Как видим, это обычная параметрическая прямая на плоскости (в 2-мерном, т.е. (m+1)-мерном пространстве):


  • на горизонтальной оси у нас лежат точки элементов (они же — значения признака X1)
  • на вертикальной — значения активации для каждого элемента
  • параметр $w_1$ — задает угол наклона,
  • а $w_0$ — сдвиг по вертикальной оси (вот и разгадка к сдвиговому нейрону).
w0 = -1.1
w1 = 0.4

# активация
y_ = w0 + w1*X1

# функция активации (вход для кванзистора - пороговой функции предсказания класса)
plt.plot(X1, y_, color='violet', lw=3,
        label=u'активация: w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2))

# порог: пересечение активации с Ф=0
plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u'порог активации')

# проекция обучающих точек на линию активации
plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200,
        label=u'активация: класс-1 (y=1)')
plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200,
        label=u'активация: класс-2 (y=-1)')


6elompwqerwar1sc60uluyin0lo.png

Вспомним еще, что после небольшого преобразования у нас порог активации обратился в ноль. Таким образом, если проекция i-го элемента на линию активации оказывается ниже нуля, мы назначаем элементу класс »-1» ($\hat{y} = -1$), если выше нуля, назначаем элементу класс »1» ($\hat{y}=1$).

Фиолетовая точка — пересечение линии активации с осью $\Phi=0$, разделяющая элементы из разных классов, — это и есть та самая разделяющая гиперплоскость (для 1-мерного пространства точка — это гиперплоскость), построенная в 1-мерном (т.е. m-мерном) пространстве признаков. Как видим, для того, чтобы разделить элементы на группы, её достаточно, но для того, чтобы назначить группам классы — уже не достатоно. Для того, чтобы назначить элементам классы, нам нужна прямая (2-мерная гиперплоскость) активации, построенная в 2-д (т.е. в (m+1)-д) пространстве «признаки+активация»: направление отклонения активации от вертикальной оси будет определять класс для групп элементов, т.к. от этого зависит, окажутся ли проекции элементов на активацию выше или ниже нуля.

Меняя параметры $w_0$ и $w_1$ мы будем получать разные активационные линии. Нам нужно построить такую линию активации, т.е. найти такую комбинацию параметров $w$, при которой проекция первых двух точек обучающей выборки на линию активации окажется ниже нуля (для них значение $\hat{y}=y=-1$), а проекция оставшихся 3-х точек окажется выше нуля (для них $\hat{y}=y=1$).

Совершенно очевидно, что в нашем конкретном случае нет ничего сложного в том, чтобы построить такую линию, более того, таких линий вообще можно построить бесконечное количество. Но мы постараемся ее построить так, чтобы удовлетворялся некий критерий оптимальности (может влиять на качество будущих предсказаний), плюс должна быть возможность распространить алгоритм на многомерный случай.

Здесь так же отметим, что мы специально выбрали исходное множество точек так, чтобы его можно было такой линией разделить (для 1-д: все элементы первой группы меньше, все элементы второй группы больше некоторого фиксированного значения), т.е. множество обучающих точек линейно разделимо.

Добавим на график еще две горизонтальные линии, соответствующие классам {1, -1}, и спроецируем на них элементы.

# горизонтальные линии для меток классов (y=1, y=-1)
plt.plot(X1, np.full(len(X1), 1), color='blue', label=u'метка: класс-1 (y=1)')
plt.plot(X1, np.full(len(X1), -1), color='red', label=u'метка: класс-2 (y=-1)')

# обучающие точки на линиях меток классов (y=1, y=-1)
plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200,
        label=u'ответ y: класс-1 (y=1)')
plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200,
        label=u'ответ y: класс-2 (y=-1)')


66xagdqpiyl-wljdjisroqngj7k.png

Точки с классом »-1» проецируем на нижнюю линию $\Phi=-1$, точки с классом »1» проецируем на верхнюю линию $\Phi=1$.

Обратим здесь внимание на еще один небольшой нюанс. По вертикальной оси мы строим значения активации, пространство значений активации непрерывно. Но результат работы классификатора (функция активации, пропущенная через порог) — дискретное множество из двух элементов {-1, 1}, а не непрерывная шкала. Здесь мы берем дискретное множество классов $y$ и накладываем его на непрерывную шкалу активации $\Phi$ так, что дискретные значения классов становятся обычными точками на шкале активации — частными случаями значений активации, которые она может непосредственно принимать или приближаться к ним достаточно близко. Строго говоря, мы могли бы изначально в качестве классов взять не числовые значения, а строковые метки «класс-1» и «класс-2», в таком случае мы бы должны были поставить в соответствие строковым меткам числовые значения на шкале активации. Поэтому и в нашем случае значения классов »-1» и »1» следует воспринимать скорее не как метки классов как есть, а как отображение помеченных классов на шкалу активации.


Пришло время ввести метрику ошибки

# линии ошибок - расстояния от точек на линии активации
# до горизонтальных линий меток классов
plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err')


roj8suhdkeh7ddtuoel3z6l47ye.png

Естественно принять, что чем ближе окажется значение активации для выбранного элемента к значению класса для этого же элемента, тем лучше активация предсказывает для этого элемента его класс. Таким образом, за ошибку для выбранного элемента можно принять расстояние между точками — вертикальной проекцией элемента на линию активации и проекцией элемента на горизонтальную линию его известного (истинного) класса. На графике: ошибки — вертикальные оранжевые линии.


Функция стоимости (потерь)

У нас есть метрика ошибки для каждого отдельного элемента. Мы можем получить из нее метрику качества для всей линии активации. Вполне естественно принять, например, что чем меньше сумма ошибок всех элементов обучающей выборки, тем лучше у нас построена линия активации. Для каждого отдельного элемента ошибка будет не минимальной, но для всей обучающей выборки в целом можно получить некий компромисс.

Но можно взять не простую сумму ошибок, а сумму ошибок, возведенных в квадрат (сумма квадратичных ошибок, sum of squared errors, SSE). Вполне очевидно, что, как и в случае с суммой обычных ошибок, чем ближе линия активации находится к точкам с истинными классами элементов, тем меньше будет и сумма квадратичных ошибок, но в случае с квадратичной ошибкой наиболее удаленные элементы будут получать более серьезный штраф.

На самом деле нас здесь больше интересует не размер штрафа за дальние элементы, а тот факт, что квадратичная функция имеет минимум и при этом везде дифференцируема (у обычной суммы будет минимум, но в этом минимуме она не будет дифференцируема), зачем это нужно, увидим чуть потом.

Итак:


  • Ошибка — расстояние от значения метки класса до гиперплоскости активации
  • SSE — сумма квадратичных ошибок всех элементов обучающей выборки
  • Функция стоимости $J(w)$ — метрика качества для выбранной линии активации. Чем меньше значение стоимости, тем лучше активация.

Возьмем в качестве функции стоимости $1 \over 2$ SSE, в общем случае и для линейного нейрона она будет выглядеть так:

$\begin{gathered} J(w) = {1 \over 2} SSE = {1 \over 2}\sum _{i=1}^{n} (\Phi (\sum _{j=0}^{m}w_{j}x_{j}^{(i)}) - y^{(i)})^{2} ={1 \over 2}\sum _{i=1}^{n} (\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} \end{gathered}$

($1 \over 2$ перед SSE, во-первых, не мешает, во-вторых, для удобства — она дальше красиво сократится)

Здесь $i$ — номер элемента, а $n$ — количество элементов в обучающей выборке. Напомню, что $y^{(i)}$ — истинный класс $i$-го элемента обучающей выборки, т.е. заранее известный правильный ответ.

Как мы помним, положение линии активации определяют параметры — весовые коэффициенты $w$, поэтому вектор $w$ выступает в качестве параметра функции потерь.


Для 1-мерного случая

$ J(w)={1 \over 2} SSE = {1 \over 2}\sum_{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})^{2} $

Значения $x$ и $y$ заранее известны (это обучающая выборка), поэтому фиксированы. Мы подбираем параметры $w$, т.е. $w_0$ и $w_1$ так, чтобы значение $J(w)$ получилось минимальным. Попробуем построить график, как значение $J(w)$ зависит от параметров $w_0$ и $w_1$

# наиболее удачный по наглядности диапазон
w0 = np.linspace(-10, 10, 200)
w1 = np.linspace(-1, 1, 200)

# https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html
# https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously
ww0, ww1 = np.meshgrid(w0, w1)

sse = []
for j in range(len(w1)):
    sse.append([])
    for i in range(len(w0)):
         sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum())
sse = np.array(sse)

# https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html
# https://matplotlib.org/api/toolkits/mplot3d.html
from mpl_toolkits.mplot3d import axes3d

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

ax.set_xlabel('w0')
ax.set_ylabel('w1')
ax.set_zlabel('J(w)')

#ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8)
ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8,
        label='SSE/2')

plt.xlim(-10., 10.)
plt.ylim(-1., 1.)

plt.legend()
plt.show()


e_-wy-7dvjycxcajavox0cyiacg.png

В общем, здесь уже видно, что у функции потерь есть минимум, и где он примерно находится. Но давайте сделаем еще один фокус и построим тот же график, только с логарифмической вертикальной шкалой.

#ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8)
ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8,
        label='log(SSE/2)')


bqvvchahkyxfbyqewajiwpus-sy.png
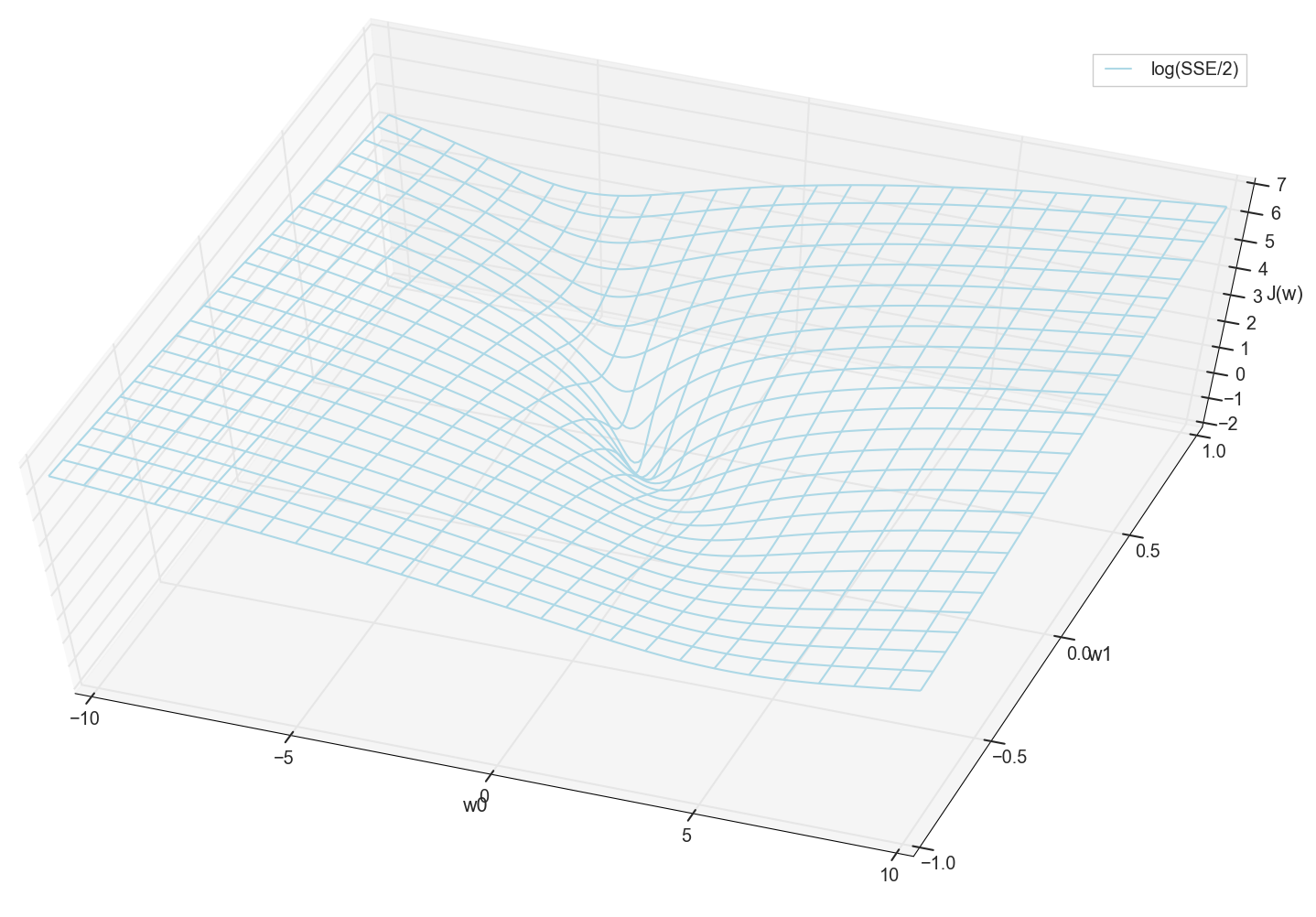
89y4us72md7_rx8xxciqis3dq9k.png

Не знаю, как вы, а лично я, когда увидел этот график в первый раз, испытал просветление. Эта натуральная впадина — не просто образная визуализация многомерных холмов из популярной статьи о нейронных сетях, это реальный график.

Наша задача — подобрать такие значения $w_0$ и $w_1$, чтобы попасть на дно этой ямы. Получим значения весовых коэффициентов — получим обученный нейрон.

Раз уж мы все равно построили график и воочию наблюдаем его минимум, никто нам не запретит найти его координаты простым перебором на сетке «вручную»: 

# найдем минимальное значение на сетке
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin
# https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html
min_ind = np.unravel_index(np.argmin(sse), sse.shape)
# точка - минимум
#ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100,
ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2),
    color='red', marker='o', s=100,
    label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2))


cmd4-zdwqeexsxkn_xwguu7w5lg.png
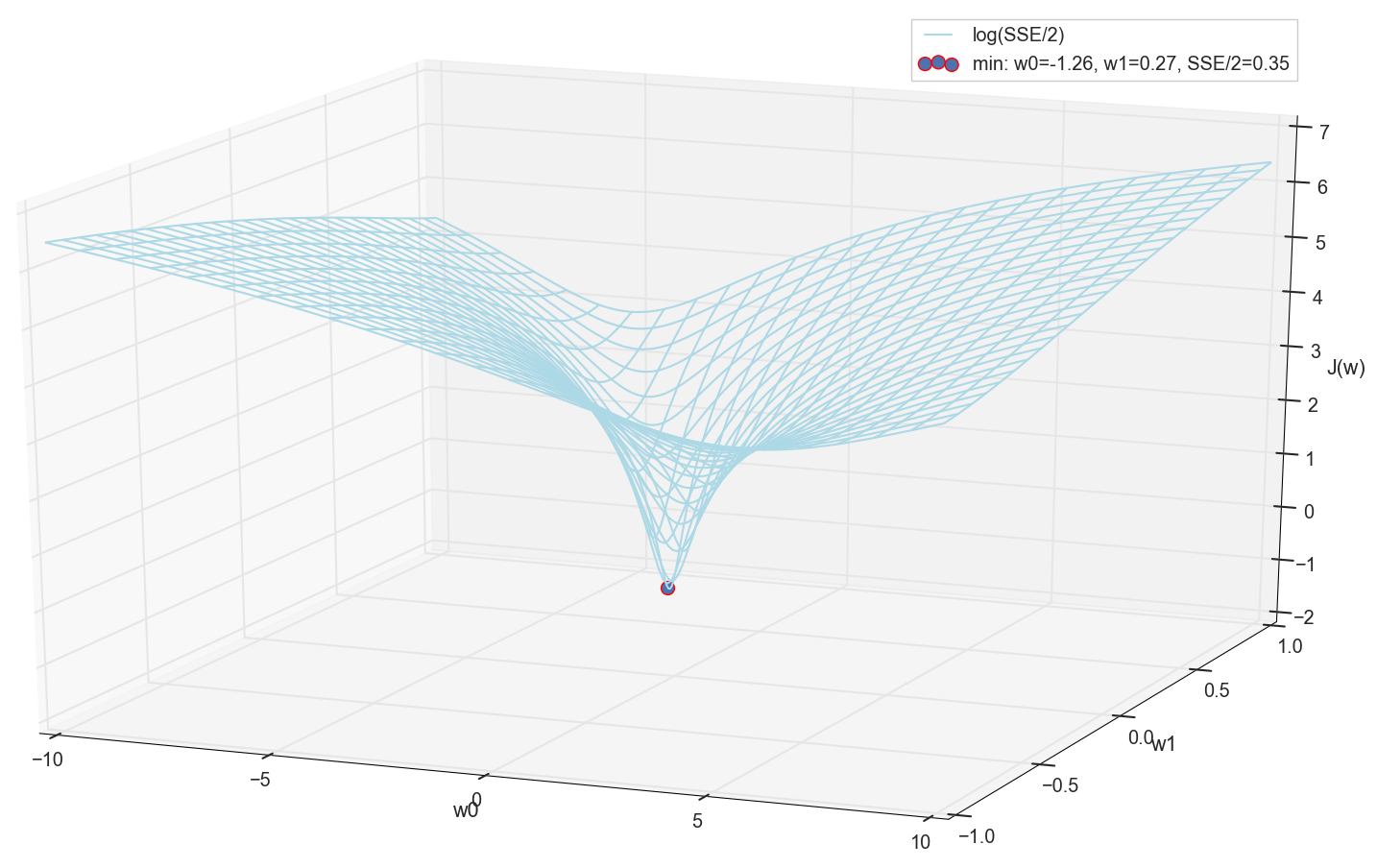
mdpa6tiw3s5roy2cnldagd1lqhq.png

Это значения: $w_0 = -1.26$ и $w_1 = 0.27$, сумма квадратичных ошибок SSE при этом 0.69, функция стоимости $J(w)=SSE/2=0.35$ (более точно: 0.3456478371758288).

Посмотрим, как с этими параметрами выглядит активация: 

# оптимум "вручную" по сетке (SSE=0.69, sse/2=0.345)
w0 = -1.26
w1 = 0.27


fgvvbajhvnbgzy_lwstajznf8y4.png

Как по мне, вполне норм. Точка пересечения активации с нулевым порогом разделяет элементы из разных классов, а сама активация назначает им правильные значения. При этом активация, похоже, находится в некотором оптимальном положении.

Перед тем, как двигаться дальше, еще раз полюбуемся на график на сетке пошире:


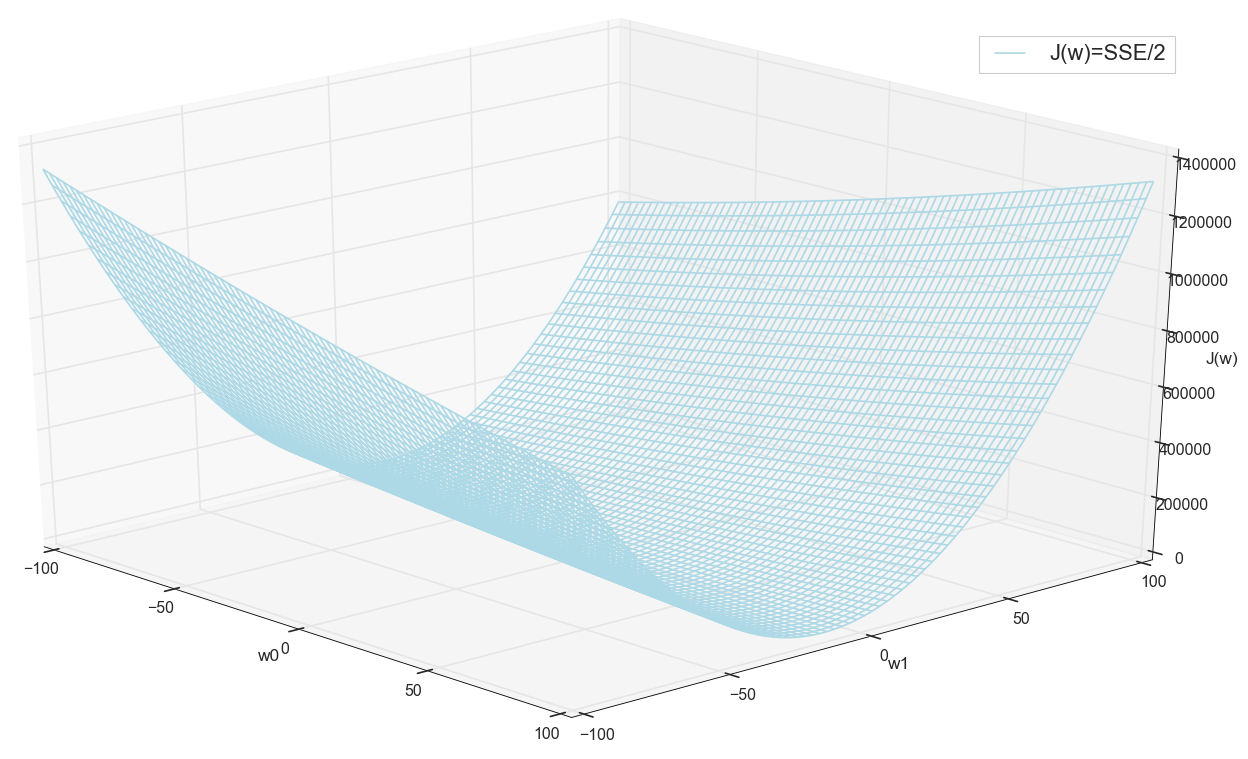
imgdb6n0ecur6tslrxrc--phmoo.png
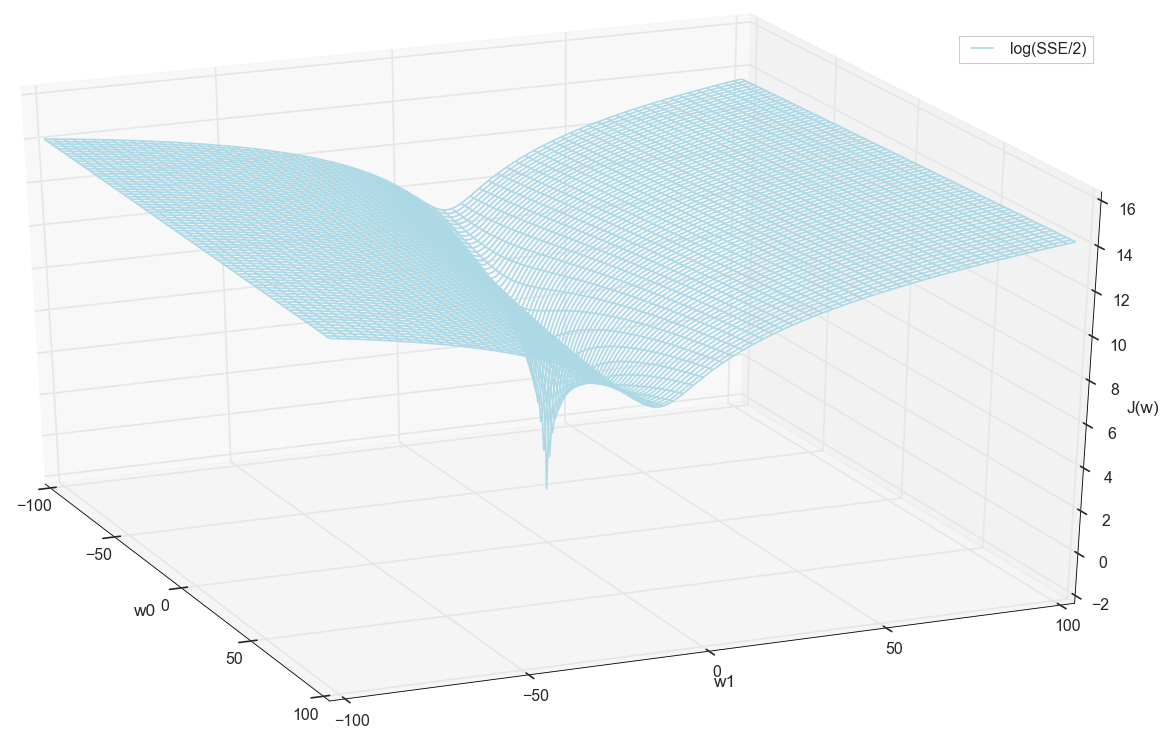
-k57retfybmgmishijatmg4o8yo.png

Похоже, что никаких других минимумов поблизости нет, кто бы мог подумать.


Поиск минимума

Итак, мы получили весовые коэффициенты — координаты минимального значения ошибки. Это будет оптимальное значение весовых коэффициентов на обучающей выборке. Вообще говоря, именно это нам и нужно, можно сказать, что нейрон обучен. Может на этом можно и завершить?


Поиск минимума: перебор по сетке


  • Вариант на первый взгляд вполне рабочий (как видим)
  • Нужно заранее знать область, где искать минимум (можно взять достаточно большие границы, затем сужать область поиска — это только на глаз)
  • Для повышения точности нужно уменьшать шаг → еще больше точек (решение: можно итеративно сужать область поиска)
  • Слишком много точек (для 2д может и ок, но для многомерных случаев очень быстро упремся в ресурсы)
  • Для MNIST (28×28=784 пикселей — столько же входов, столько же весовых коэффициентов, сетка 100 шагов на размерность): 100^784=10^785.

Значит, если мы захотим обучить один-единственный нейрон (даже не нейросетку) на изображении 28×28=784 пикселей методом поиска минимума прямым перебором на сетке в 100 точек на каждое измерение, нам нужно перебрать 10^785 комбинаций. Это довольно много и для хранения, и для перебора (в видимой части Вселенной всего 10^80 атомов, Вселенная существует примерно 4×10^17 секунд = 4×10^26 наносекунд).

Попробуем найти вариант побыстрее.


Поиск минимума: спуск с постоянным шагом

Посмотрим на график функции потерь $J(w)$ на плоскости: фиксируем $w_0$, меняем $w_1$

def sse_(X, y, w0, w1):
    return ((w0+w1*X - y)**2).sum()

# фиксируем w0, строим график J(w1)=sse(w1)/2
w1 = np.linspace(-1, 1, 200)

sse = [[], [], []]
for i in range(len(w1)):
    sse[0].append(sse_(X1, y, -1, w1[i]))
    sse[1].append(sse_(X1, y,  0, w1[i]))
    sse[2].append(sse_(X1, y,  1, w1[i]))
sse = np.array(sse)

plt.plot(w1, sse[0]/2, color='orange', label='w0=-1')
plt.plot(w1, sse[1]/2, color='blue', label='w0=0')
plt.plot(w1, sse[2]/2, color='red', label='w0=1')

plt.xlabel('w1')
plt.ylabel('J(w)')

plt.legend()
plt.show()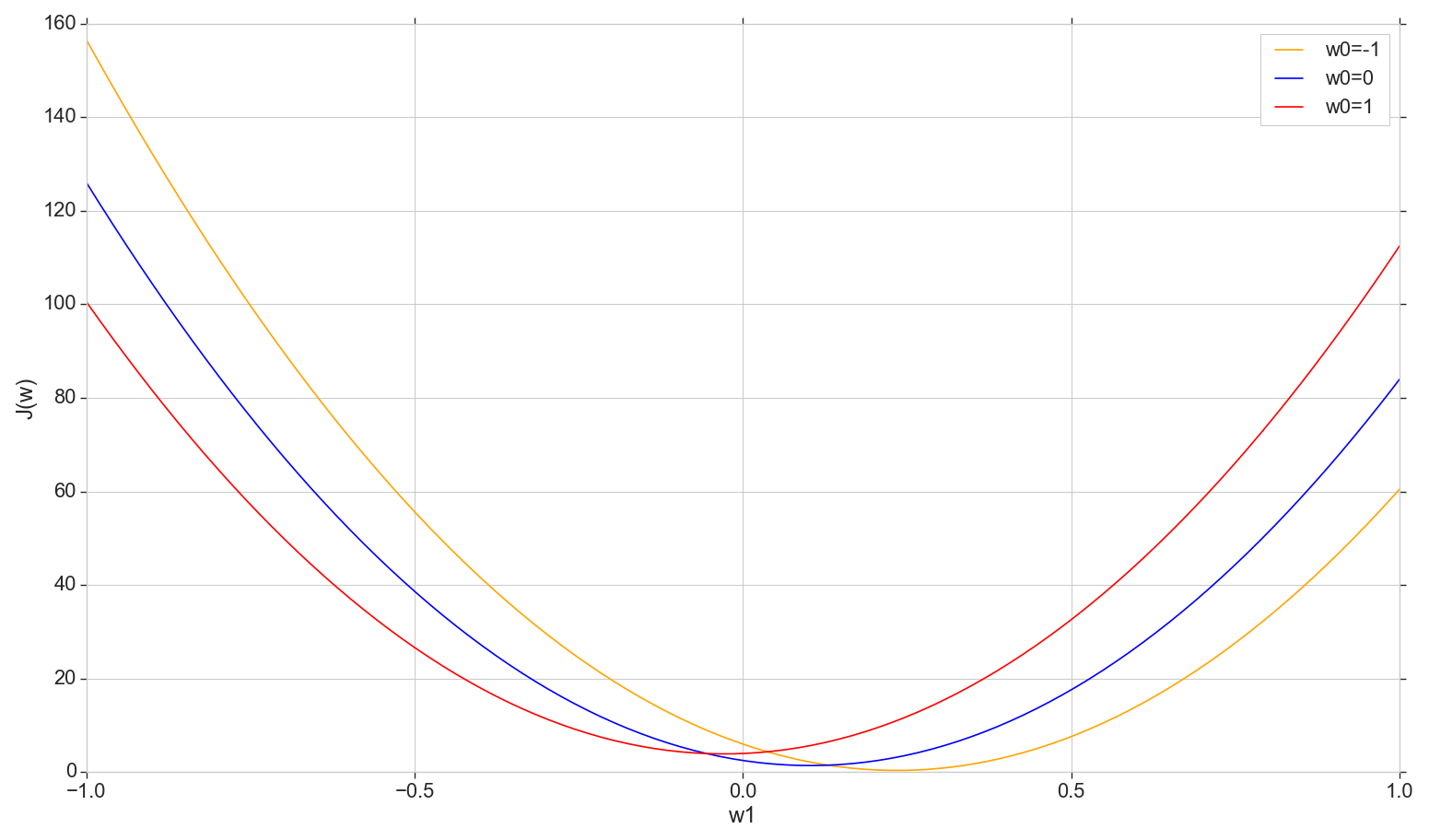


bwfx-xg_gpsabu83owx7ldokvki.png

Это обычная парабола (точнее, семейство парабол — они будут немного отличаться в зависимости от того, какое именно значение зафиксировали на $w_0$). Чтобы найти минимум параболы, не обязательно перебирать все точки. Мы можем выбрать произвольную точку на горизонтальной оси и двигаться в сторону минимума с некоторым шагом.

Рассмотрим вариант с постоянным шагом


  • Если шаг слишком большой, можно промахнуться, так и не подступившись к минимуму (шаг можно уменьшить)
  • Если слишком маленький, будет слишком много шагов (больше, чем могло бы быть)
  • Точный минимум мы в любом случае не достигнем, но можем достигнуть с произвольной точностью, поменяв около найденного неточного минимума шаг (шаг перестает быть постоянным)
  • Не знаем направление спуска (можно решить алгоритмически: не шагать в сторону увеличения ошибки)
  • Проблема с поиском диапазона решена (можно спускаться из любой точки — рано или поздно все равно спустимся вниз)
  • В принципе, вариант рабочий, но может есть вариант получше?

Замечание: когда я рассказывал про такой вариант спуска на лекции, один студент спросил, зачем нужно двигаться по шагам, если можно сразу найти минимум параболы по формуле? Я сначала ответил что-то в духе, что нам сейчас интересно рассмотреть вариант с итерациями, чтобы потом иметь возможность применить его не только с параболой, но и в других ситуациях. Плюс к этому, на самом деле нам не нужен минимум параболы конкретно на этом срезе — мы будем двигаться к минимуму не по одному измерению, а по всем измерениям поочередно так, что на каждой новой итерации новый шаг будет проходить не по этой параболе, а на параболе с нового среза со сдвинутым значением $w_0$. Но подумав позднее, я подумал, что в принципе нет ничего плохого, если мы на каждом срезе будем двигаться не шагами, а скатываться сразу к минимуму текущего среза. Так раз за разом измерение за измерением мы должны все равно скатиться к глобальному минимуму, и, похоже, быстрее, чем по шагам. Для единственного нейрона должно сработать, и не только с параболой. Но я пока не стал тратить время на проверку этой теории, поэтому здесь просто двинемся дальше — я обещал рассказать про градиентный спуск.


Поиск минимума: градиентный спуск

В общем так, спускаемся по шагам, но делаем это более умно. Используем для подбора шага производную кривой стоимости (здесь не кривая стоимость, а кривая стоимости).

Это всё хорошо, но причем здесь производная? Сейчас разберемся.


Геометрический смысл производной

Для меня производная долгое время оставалась набором специальных формул и правил для ее вычисления, плюс что-то про возрастание, убывание и экстремумы. Здесь будет уместно вспомнить или выяснить, что из себя представляет производная на самом деле.

Производная функции $y(x)$ в данной точке $x_0$ — это предел отношения приращения функции $\Delta y$ к приращению аргумента $\Delta x$ при приращении аргумента $\Delta x$, стремящемся к нулю:

$ y'(x_0) = \lim_{\Delta x \to 0} {\Delta y \over \Delta x}, \Delta y = y(x_0 + \Delta x) - y(x_0) $


hfpkkugsu-439fauq43hrsied-o.png

На картинке точка $M (x_0, y(x_0)) = (x_0, y_0)$ — точка, в которой мы хотим определить производную. Точка $N (x_0+\Delta x, y(x_0 + \Delta x)) = (x_0+\Delta x, y_0 + \Delta y)$ — точка, получаемая приращением аргумента $\Delta x$. Прямая $MN$ — секущая, проходящая через эти две точки.

Точка $A$ — пересечение секущей $MN$ с горизонтальной осью $y=0$.

Рассмотрим два прямоугольных треугольника: треугольник $\triangle NPM$ с участком секущей $MN$ в качестве гипотенузы и треугольник $\triangle MBA$ с продолжением секущей до оси $y=0$ — отрезком $AM$ в качестве гипотенузы. Из графика и школьного курса геометрии очевидно, что углы $\angle NMP$ и $\angle MAB$ равны, а значит равны и их тангенсы:

$ \tan \angle MAB = \tan \angle NMP = {MB \over AB} = {NP \over MP} = {\Delta y \over \Delta x} $

Добавим на картинку: $MD$ — касательная к исходной кривой в точке $M$, пересекает ось $y=0$ в точке $D$. Треугольник $\triangle MBD$ — прямоугольный треугольник с гипотенузой — участком касетельной, отрезком $MD$.

Устремляем приращение $\Delta x$ к нулю:


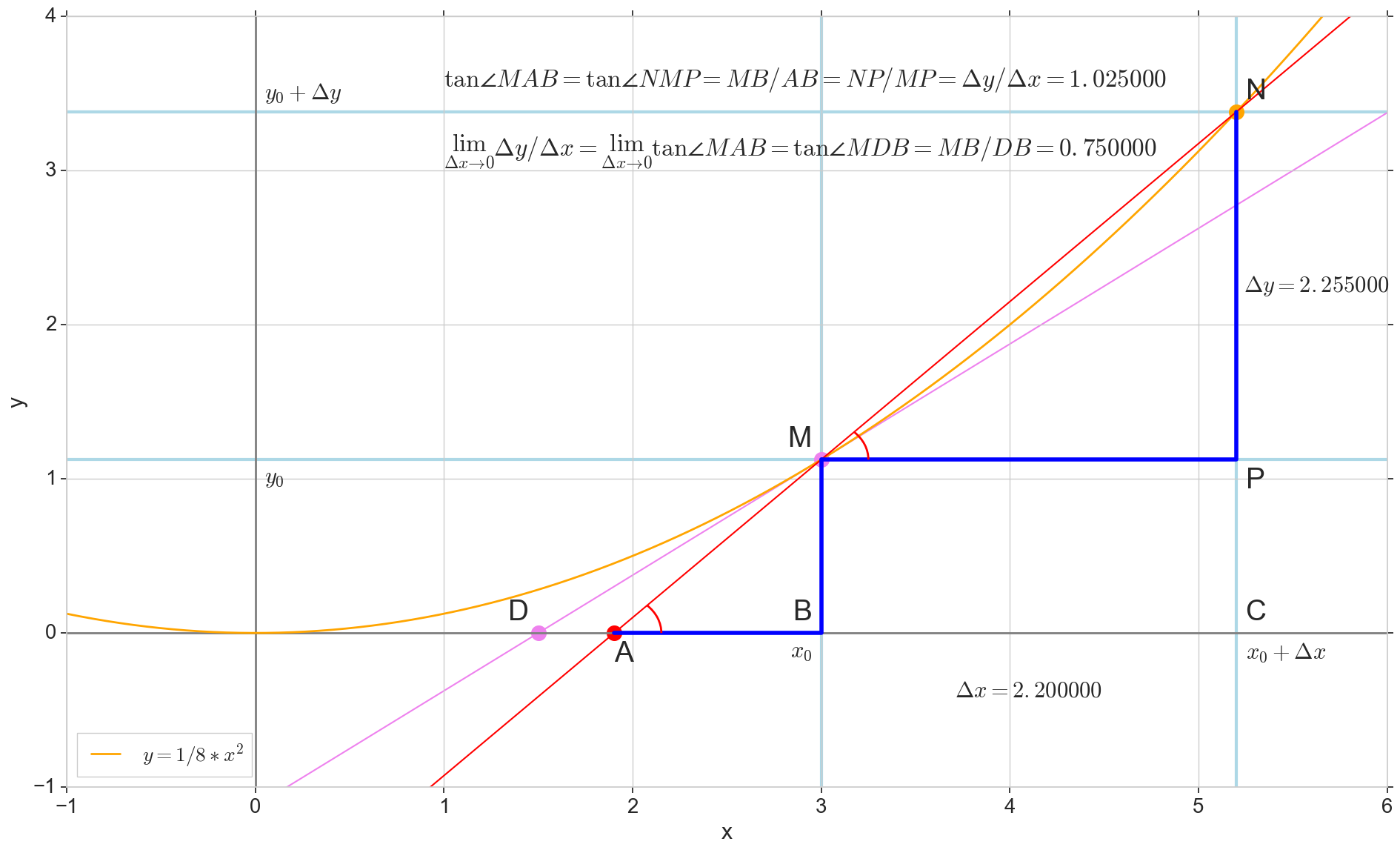
ordrjpmpgw10u0hoejeeekf-mmq.png

Точка $N$ съезжает в точку $M$ по функции, точка $A$ ползет в точку $D$, секущая $MN$ превращается в касательную $MD$ с точкой касания $M$. Исходный треугольник $\triangle NPM$ с катетами $\Delta x$ и $\Delta y$ сжимается в точку, но подобный ему треугольник $\triangle MBA$ превращается в треугольник © Habrahabr.ru