Главные отличия PCA от UMAP и t-SNE
Здесь будет рассказано о главных отличиях самого старого и базового алгоритма снижения размерности — PCA от его популярных современных коллег — UMAP и t-SNE. Предполагается, что читатель уже предварительно что-то слышал про эти алгоритмы, поэтому подробного объяснения каждого из них в отдельности приведено не будет. Вместо этого будут объяснены самые важные для практики свойства этих алгоритмов и то, на какие связанные с ними подводные камни можно налететь при неосторожности. Все особенности будут описаны на примерах, с минимумом теории; те пытливые умы, что почувствуют в процессе чтения жажду математической строгости, смогут удовлетворить её в литературе, ссылки на которую будут даны по ходу дела и в конце статьи.
Вот главная таблица, вокруг которой будет строиться моё повествование:
Таблица 1 — отличительные свойства PCA, UMAP и t-SNE
Свойства \ Алгоритм | PCA | UMAP | t-SNE |
Линейность | Да | Нет | Нет |
Детерминированность | Да (условно) | Нет | Нет |
Обучаемость | Нет (условно) | Да | Да |
Выявляет структуру | Только глобальную | Локальную, отчасти глобальную | Локальную, отчасти глобальную |
Скорость работы | Быстрый | Средний | Медленный |
Таблицу я привожу в самом начале, чтобы потом было легко ее находить и обращаться к ней по мере чтения статьи. А теперь обо всем по порядку!
Введение
Для начала вспомним, что делают алгоритмы снижения размерности в принципе. Каждый такой алгоритм принимает на вход набор точек в пространстве размерности побольше (допустим, N), а выдаёт набор из того же количества точек, но в пространстве размерности поменьше (допустим, M). Строго говоря, M ≤ N.
Например, всем известный датасет MNIST состоит из черно-белых картинок 14×14, а значит, каждую картинку из набора можно полностью описать 14×14 = 784 числами, каждое из которых будет содержать значение яркости одного из пикселей. Можно считать эти 784 числа координатами некоторой точки — тогда каждой картинке из MNIST будет сопоставлена точка в пространстве соответствующей размерности (N = 784). С помощью алгоритмов снижения размерности можно отправить множество таких точек на плоскость (M = 2) и посмотреть на их распределение глазами:

Применение PCA, t-SNE, UMAP для визуализации MNIST

В данном случае можно глазами увидеть кластеры из точек, соответствующих примерам с одинаковыми метками (обозначены точками одинакового цвета), при чем после применения разных алгоритмов эти кластеры выглядят по-разному. Некоторые из отличительных особенностей исходного множества точек после преобразования сохраняются, а некоторые — теряются. То, какие именно особенности множества сохранятся, зависит от свойств самого алгоритма. Далее мы последовательно разберем эти свойства (см. Таблицу 1) и начнём с самого простого — с линейности.
Линейность
Чтобы проиллюстрировать смысл линейности, перейдем к простому синтетическому примеру — такому, где N = 2, а M = 1 (совсем маленькая размерность, жесть!). Он представляет из себя две группы точек, сосредоточенных вокруг центров, находящихся на некотором расстоянии друг от друга. В данном случае простейшим (хотя и довольно бесполезным) примером алгоритма уменьшения размерности будет проекция точек плоскости на одну из координатных осей:

Примеры линейных преобразований — проекции на оси; в данном конкретном примере проекция на ось y лучше демонстрирует кластерную структуру датасета, чем проекция на ось x.
По сути, эти проекции представляют из себя просто зануление одной из координат наших точек. Например, если у нас есть три точки: v1 = (x1, y1), v2 = (x2, y2), то их проекции на ось x можно представить как p1 = (x1, 0), p2 = (x2, 0). Далее, как известно из основ линейной алгебры, вектора, соответствующие этим точкам, можно складывать друг с другом и вычитать друг из друга. Например, с помощью такого сложения можно создать новую точку v3 = v1 + v2: её координаты будут равны (x1 + x2, y1 + y2). При этом, очевидно, будет выполняться и равенство проекций: p3 = p1 + p2; таким образом, можно сказать, что сложение как бы «пробрасывается» через операцию проекции. То же самое будет выполняться для вычитания и умножения на коэффициент. Это свойство и называется линейностью.
В векторной записи проекцию точки (или вектора) (x, y) на оси X и Y можно записать как умножение на матрицы специального вида:

Запись проекции с помощью умножения на матрицу
В курсе линейной алгебры доказывается, что свойством линейности будут обладать не только проекции на координатные оси, но и все остальные преобразования пространства, которые можно записать в виде умножения на какую-то матрицу.
Возвращаясь к нашим алгоритмам: преобразование с помощью PCA тоже записывается умножением на матрицу, а значит, является линейным. При этом не имеет значения, сколько именно компонент PCA мы отбросим в процессе уменьшения размерности, а сколько оставим — как мы уже поняли из примера выше, отбрасывание компонент также является линейным преобразованием, а композиция любого количества линейных преобразований линейна (проверьте сами или загляните в учебник).
На практике это означает, что если на исходном датасете была задана какая-то осмысленная арифметика (то есть, если элементы датасета можно было осмысленно складывать друг с другом и вычитать друг из друга), то после применения PCA она сохранится. В качестве примера датасета с аримфметикой можно взять эмбеддинги слов, сделанные с помощью word2vec с классическими приблизительными равенствами в духе king — man + woman ≈ queen (другие примеры подобных приблизительных равенств в этом пространстве см., например, здесь — https://www.technologyreview.com/2015/09/17/166211/king-man-woman-queen-the-marvelous-mathematics-of-computational-linguistics/). В комментариях можете поделиться другими примерами датасетов с приблизительной или даже точной арифметикой, которые вам попадались в работе — возможно, найдется пример и получше.
При этом, UMAP и t-SNE задаются более сложными формулами, чем PCA, и линейными не являются. Так что после них сохранить арифметику на датасете, в общем случае, нельзя (если где-то она и сохранится, то это будет случайностью).
Детерминированность
Ну, здесь все ещё проще: UMAP и t-SNE являются стохастическими алгоритмами по своей природе — то есть, включают в себя расчеты, основанные на (псевдо)случайных числах. А вот результат PCA мы можем посчитать однозначно безо всякого влияния случайности (надо отметить, что на практике, расчет PCA может включать в себя стохастический алгоритм вычисления SVD, но от этого можно и отказаться — см. документацию https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html).
Фактически это означает, что рассчитывать на надёжную воспроизводимость результатов, полученных с помощью t-SNE и UMAP, не приходится. Особенно чувствителен к случайности t-SNE — вот простенький пример нестабильности t-SNE на одних и тех же данных:

Результаты разных запусков t-SNE. Источник — » Understanding How Dimension Reduction Tools Work: An Empirical Approach to Deciphering t-SNE, UMAP, TriMap, and PaCMAP for Data Visualization»
В качестве исходных данных тут выступает синтетический двумерный датасет, состоящий из точек на кривой. Отображается все это снова на плоскость (помните, что M = N не запрещается, то есть, и исходное, и итоговое пространство на самом деле могут иметь одинаковую размерность?). Как видно, результаты разных запусков могут быть совсем не похожи друг на друга.
А вот пример с несколько более стабильным UMAP на уже знакомом нам MNIST:

Результаты разных запусков UMAP на MNIST. Источник — https://umap-learn.readthedocs.io/en/latest/reproducibility.html
Здесь отличия уже не такие сильные, но и их легко заметить, слегка присмотревшись.
В теории, мы можем зафиксировать начальное состояние генератора псевдослучайных чисел и получать одни и те же результаты для одних и тех же расчетов, которые этот генератор задействуют. Для этого можно устанавливать фиксированный random seed в numpy или передавать random_state напрямую в функции, реализующие алгоритмы UMAP и t-SNE. Однако, функции, реализующие UMAP и t-SNE для питона, под капотом используют генераторы псевдослучайных чисел из того же sklearn — см. https://github.com/lmcinnes/umap/blob/master/umap/parametric_umap.py, https://github.com/scikit-learn/scikit-learn/blob/872124551/sklearn/manifold/_t_sne.py. А в разных версиях sklearn и numpy имплементации одних и тех же методов могут меняться, так что одни и те же random seeds могут выдавать разные результаты — то есть, сохранение воспроизводимости не гарантируется после очередного обновления версии библиотек. Более того, результаты могут различаться даже на разных операционных системах — см. https://github.com/lmcinnes/umap/issues/153 . Это значит, что полную гарантию воспроизводимости можно получить, только запуская скрипт с расчетами в одном и том же контейнере, где гарантируется наличие одной и той же ОС и окружения.
Из-за этого недостатка предсказуемости, я бы не советовала использовать UMAP и t-SNE в серьезных пайплайнах для обработки данных. Эти инструменты подходят скорее для визуализации данных и, возможно, предварительных расчетов.
Обучаемость и локальность/глобальность структуры
PCA — самый простой из рассматриваемых алгоритмов и в Таблице 1 обозначен как условно необучаемый. Почему же условно? Дело в том, что на практике у PCA под капотом зачастую используют итеративный численный метод нахождения SVD-разложения — этот метод работает намного быстрее, чем его не-итеративный, точный аналог. Однако, использование итеративности не обязательно, и этот метод можно заменить на точный ценой повышения длительности вычислений. UMAP и t-SNE в этом аспекте сильно отличаются: они являются обучаемыми по самой своей сути. На каждом шаге обучения эти алгоритмы улучшают свой результат, делая полученное представление более информативным. Кроме того, у них есть гиперпараметры, которые очень сильно на этот результат влияют.
Главным гиперпараметром t-SNE можно считать perplexity (перплексию), а главным гиперпараметром UMAP — n_neighbors (число соседей). В процессе обучения оба алгоритма ищут для каждой точки датасета оптимальное (по своему мнению) место в пространстве, в которое они её собираются отобразить. В расчетах положения каждой точки датасета относительно ближайших соседей в новом пространстве, они используют её положение относительно ближайших соседей в старом пространстве. Так вот, параметры perplexity и n_neighbors играют похожую роль: они оба устанавливают, сколько именно соседей каждой точки будет при этом задействовано.
Вот пример результатов работы t-SNE и UMAP на датасете MNIST с разными гиперпараметрами:
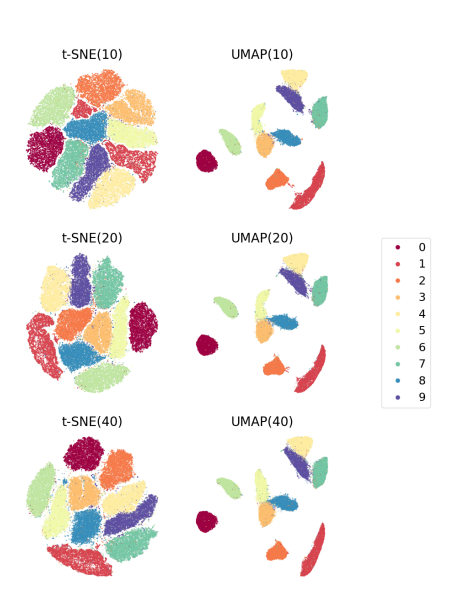
Влияние гиперпараметров на результаты (MNIST). Источник — «Understanding How Dimension Reduction Tools Work: An Empirical Approach to Deciphering t-SNE, UMAP, TriMap, and PaCMAP for Data Visualization»
Здесь в скобках написаны соответствующие значения perplexity для t-SNE и n_neighbors для UMAP. Как видно, для датасета MNIST влияние получается не очень заметное. Но что будет для других наборов данных?

Влияние гиперпараметров UMAP (Mammoth). Источник — «Understanding How Dimension Reduction Tools Work: An Empirical Approach to Deciphering t-SNE, UMAP, TriMap, and PaCMAP for Data Visualization»
На этой картинке изображено влияние n_neighbors на поведение UMAP на синтетическом датасете: облаке точек в форме мамонта, вложенного в трехмерное пространство. Как видно, чем больше значение n_neighbors (количество задействованных при расчете соседей), тем лучше алгоритм учитывает не только локальную, но и глобальную структуру облака точек. Если еще сильнее увеличить количество соседей, глобальная структура расплющенного мамонта станет еще более явно выражена:

Влияние гиперпараметров UMAP, Mammoth. n_neighbors = 200
А вот результаты работы t-SNE для трех других синтетических датасетов:

Как видно, в большинстве случаев большая перплексия и здесь позволяет выделить более глобальные свойства изучаемого облака точек.
Кроме этого, у UMAP есть еще один довольно важный параметр под названием min_dist:

UMAP на PenDigits. Источник — «UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction»
Этот параметр влияет на то, насколько близко друг к другу будут находиться соседние точки датасета в итоговом пространстве. Например, на картинке выше показано, как этот параметр совместно с уже знакомым нам n_neighbors влияет на вложение датасета рукописных цифр PenDigits (этот датасет тоже представляет из себя картинки с записями цифр, но не такие, как в MNIST). Если мы устанавливаем в качестве min_dist значение побольше, наши точки меньше «слипаются», но зато и кластерная структура датасета становится менее заметной.
Что же касается PCA — как уже было сказано, для него подобных механизмов регуляции нет. Формулы для вычисления PCA задействуют все точки исходного датасета сразу, поэтому можно сказать, что он выделяет только глобальную структуру датасета.
Скорость работы
Думаю, это наиболее простой и понятный аспект работы алгоритмов. UMAP работает намного быстрее t-SNE, а PCA, благодаря своей простоте, работает намного быстрее, чем UMAP. Поэтому при работе с датасетами очень высокой размерности часто используют следующий пайплайн: сначала применяют простой советский PCA для уменьшения размерности до той величины, с которой сможет за разумное время работать UMAP или t-SNE, а потом уже применяют сам UMAP или t-SNE.
Что ж, надеюсь, мой рассказ был вам полезен и помог лучше разложить по полочкам информацию про важные для практики особенности PCA, UMAP и t-SNE. Если же возникло желание узнать про алгоритмы снижения размерности побольше, существует огромное количество материалов, по которым можно при желании практически бесконечно углубляться в эту тему. Я рекомендую при этом начать с красивых наглядных демонстраций и видео, которые будут перечислены ниже наряду с литературой.
Что ещё почитать/посмотреть
Демонстрации:
Объяснения, как работает каждый алгоритм:
Имплементации:
Статьи, учебники:
