Генеративное Моделирование и AI01.02.2018 14:33

В предыдущей главе мы поговорили о классических дискриминативных моделях в машинном обучении и разобрали простейшие примеры таких моделей. Давайте теперь посмотрим на более общую картину.

Задача Искусственного Интеллекта

Искусственный Интеллект (ИИ) — это алгоритм, умеющий решать задачи, типично решаемые людьми, на уровне сопоставимом или превосходящем человеческий. Это может быть распознавание визуальных образов, понимание и анализ текстов, управление механизмами и построение логических цепочек. Система искусственного интеллекта — это система, которая сможет эффективно решать сразу все подобные задачи. Решения этой задачи до сих пор не существует, но есть разнообразные подходы, которые можно назвать первыми шагами в направлении решения проблемы ИИ.

В двадцатом веке самым популярным был подход, основанный на правилах. Его идея заключается в том, что мир подчиняется законам, которые, например, изучает физика и другие естественные науки. И даже если их нельзя эффективно запрограммировать в ИИ напрямую, разумно предположить, что при достаточном числе запрограммированных правил, ИИ система, основанная на вычислительных машинах, сможет эффективно существовать в мире, основанном на этих правилах, и решать произвольные задачи. Этот подход не учитывает естественную стохастичность некоторых событий. Чтобы ее учесть, необходимо на этом списке правил построить вероятностную модель для принятия стохастических решений при условии случайных входных данных.

Полное описание мира потребовало бы настолько большого числа правил, что их невозможно задать и поддерживать вручную. Отсюда возникает идея провести достаточно наблюдений событий в реальном мире и вывести необходимые правила автоматически из этих наблюдений. Эта идея сразу же поддерживает как действительную стохастичность некоторых естественных процессов, так дополнительно и мнимую стохастичность, возникающую из-за того, что не до конца известно, какие факторы влияют на некий детерминированный процесс. Автоматическим выводом правил из наблюдений занимается раздел математики, называемый машинным обучением, и именно оно в данный момент является наиболее обещающим фундаментом для ИИ.

Машинно обученный ИИ

В предыдущей главе мы посмотрели на классические задачи машинного обучения (классификация и регрессия) и классические линейные методы их решения (логистическая и линейная регрессии). В реальности для сложных задач используют нелинейные модели, обычно основанные либо на решающих деревьях, либо на глубоких искусственных нейронных сетях, которые лучше себя показывают для задач обработки плотных данных с высоким уровнем избыточности: изображений, звука и текста.

Эти методы способны автоматически выводить правила на основе наблюдений, и они очень успешно применяются в коммерческих приложениях. Однако, у них есть недостаток, из-за которого они недостаточны для использования в качестве ИИ-системы — они специально разработаны для решения конкретной узкоспециализированной задачи, например, различать кошек и собак на изображении. Очевидно, что модель, суммирующая изображение в одно число, теряет много данных. Чтобы определить на изображении кошку не обязательно понимать суть кошки, достаточно лишь научиться искать основные признаки этой кошки. Задача классификации изображения не предполагает полного понимания сцены, а только поиск в ней конкретных объектов. Определить классификатор для всех возможных комбинаций связей всех возможных комбинаций объектов не представляется возможным хотя бы из-за экспоненциально большого объема наблюдений, которые нужно собрать и разметить. Потому идеи классических задач машинного обучения с подкреплением, в которых решается конкретная поставленная задача, не подходят. Для ИИ нужен принципиально иной подход к постановке задачи для машинного обучения.

Вероятностная постановка задачи понимания мира

Итак, нам нужно, имея набор наблюдений, в каком-то смысле понять процесс, их порождающий. Переформулируем эту задачу на вероятностном языке. Пусть наблюдение — это реализация случайной величины 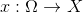, и есть набор наблюдаемых событий 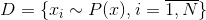. Тогда «понимание» всего разнообразия событий можно сформулировать как задачу восстановления распределения .

Есть несколько подходов к решению этой задачи. Один из самых общих методов — введение латентной переменной. Допустим, существует некое представления 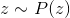наблюдения . Это представление описывает «понимание» наблюдения моделью. Например, для кадра компьютерной игры таким пониманием может служить релевантное состояние игрового мира и положение камеры. В таком случае 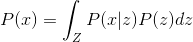. Фиксируя 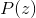так, чтобы оно было простым для сэмплирования распределением, мы получаем модель, в которо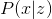й и  можно приближать нейросетями. Обучая эту модель стандартными методами глубокого обучения можно получить по формуле выше, после чего мы можем использовать ее в вероятностном выводе. Более точные формулировки таких моделей будут в последующих частях, но тут нужно заметить, что сложные версии таких моделей требуют аппроксимации сложных невычислимых интегралов, для чего обычно используются приближенные методы вроде MCMC или Variational Inference. Построение для извлечения из нее сэмплов называют задачей генеративного моделирования.

Можно подойти к вопросу иначе. На самом деле, в явном виде рассчитывать , аппроксимируя сложные интегралы, не обязательно. Одна из идей состоит в том, что если модель может «вообразить» себе мир, значит, она понимает, как он устроен. Например, если я могу нарисовать человека в разных позах и ракурсах, значит я понимаю, как устроена его анатомия и перспектива в целом. Если люди не могут отличить сгенерированные моделью объекты от настоящих, значит модель смогла честно «понять», как работает то или иное явление настолько же хорошо, насколько его понимают эти люди. Эта идея вдохновляет развитие генеративного моделирования с неявной  — разработке моделей, которые, имея конечное число наблюдений, способны обобщать их и генерировать новые наблюдения, неотличимые от настоящих. Предположим, что 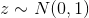, или любое другое простое для сэмплирования распределение. Тогда при достаточно общих условиях существует функция 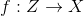, такая, что 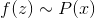. В этом случае мы не получаем в явном виде, но модель все равно содержит информацию о нем неявно. 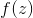Вместо восстановления можно восстановить , после чего сэмплы из  могут быть получены как 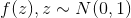. 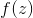нельзя использовать в вероятностном выводе напрямую, но, во-первых, это не всегда нужно, а во-вторых, когда это нужно, часто можно воспользоваться методами Монте-Карло, для которых как раз и нужно получать сэмплы. К методам этого типа относится и модель Generative Adversarial Networks, исследуемая в следующей части.

Principal Component Analysis

Давайте посмотрим на простую генеративную модель. Пусть есть некая наблюдаемая величина 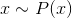. Например это может быть рост человека или пиксельное изображение. Предположим, что эта величина полностью объясняется некой скрытой (латентной) величиной 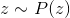. В нашей аналогии это может быть вес человека или объект и его ориентация на изображении. Предположим теперь, что для скрытой величины 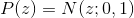, а наблюдаемое величина линейно зависит от с нормальным шумом, т.е. 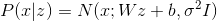. Эта модель называется Probabilistic Principal Component Analysis (PPCA) и она, по сути, является вероятностной переформулировкой классической модели Principal Component Analysis (PCA), в которой видимая переменная линейно зависит от латентной переменной без шума.

Expectation Maximization

Expectation Maximization (EM) — алгоритм для обучения моделей с латентными переменными. Детали можно найти в специализированной литературе, но общая суть алгоритма довольно проста:

1. Инициализировать модель начальными значениями параметров.
2. E-шаг. Заполнить латентные переменные их ожидаемыми значениями в текущей модели.
3. M-шаг. Максимизировать правдоподобие модели с фиксированными значениями латентных переменных. Например, градиентным спуском по параметрам.
4. Повторять (2, 3), пока ожидаемые значения латентных переменных не перестанут изменяться.

Если на М-шаге не максимизировать правдоподобие до конца, а только делать шаг в направлении максимума, это называется Generalized EM (GEM).

Решение PCA с помощью EM

Применим к нашей модели PCA EM алгоритм и метод максимума правдоподобия для поиска оптимальных параметров 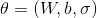модели. Совместное правдоподобие наблюдаемых и латентных параметров можно записать как:

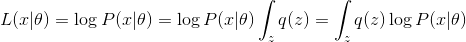
Где 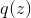 — это произвольное распределение. Далее будем опускать условность распределений по параметрам для облегчения формул.

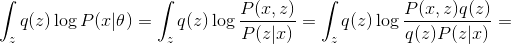
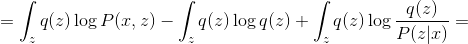
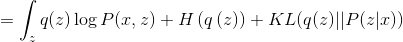
Где величина называется 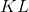-дивергенцией между распределениями 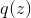и . Величина называется энтропией 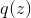. 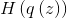не зависит от параметров , поэтому это слагаемое мы можем игнорировать при оптимизации:

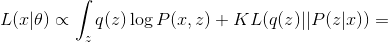
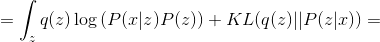
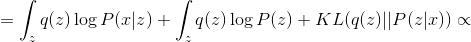
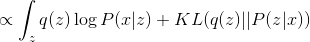
Величина 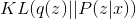неотрицательна и равна нулю когда 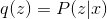. В связи с этим давайте определим следующий EM алгоритм:

1. E: 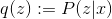. Это обнулит второе слагаемое .
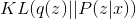2. M: Максимизация первого слагаемого .

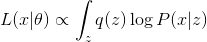PPCA — линейная модель, потому ее можно решить аналитически. Но вместо этого мы попробуем решить ее с помощью обобщенного EM-алгоритма, когда максимизация выполняется не до конца, а только одним шагом градиентного подъема в сторону оптимума. Более того, мы будем использовать стохастический градиентный подъем, т.е. его шаг будет шагом в сторону оптимума только в среднем. Так как наши данные i.i.d., то

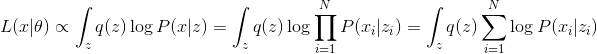
Заметим, что выражение вида 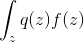является математическим ожиданием 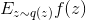. Тогда

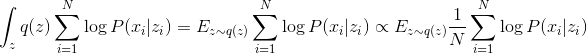
Так как единичный сэмпл является несмещенной оценкой математического ожидания, то можно приближенно записать следующее равенство:

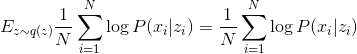
Итого, подставляя 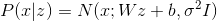, получим:

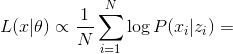
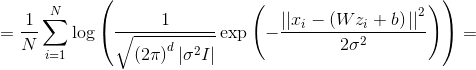
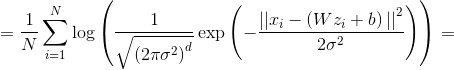
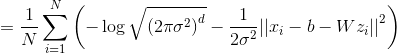
или

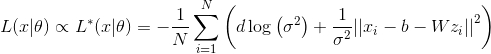
Формула 1. Функция потерь, пропорциональная правдоподобию данных в модели PPCA.

Где 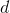 — размерность наблюдаемой переменной . Теперь выпишем GEM-алгоритм для PPCA. 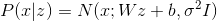, а 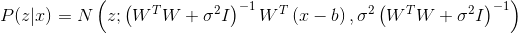. Тогда GEM-алгоритм будет выглядеть так:

1. Инициализируем параметры 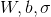разумными случайными начальными приближениями.
2. Сэмплируем 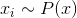 — выборка минибатча из данных.
3. Рассчитываем ожидаемые значения латентных переменных 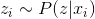или .
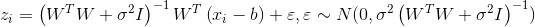4. Подставляем 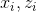в формулу (1) для  и делаем шаг градиентного подъема по параметрам. Важно помнить, что 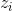 надо воспринимать как входы, и не пускать обратное распространение ошибки внутрь него.
5. Если правдоподобие данных и ожидаемые значения латентных переменных для контрольных видимых переменных не сильно изменяются, останавливаем обучение. Иначе, идем на шаг (2).

После того, как модель обучена, из нее можно генерировать сэмплы:

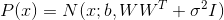
Численное решение задачи PCA

Давайте обучим модель PPCA с помощью стандартного SGD. Мы опять будем изучать работу модели на игрушечном примере, чтобы понять все детали. Полный код модели можно найти тут, а в этой статье будут освещены лишь ключевые моменты.

Положим 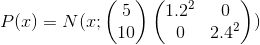 — двумерное нормальное распределение с диагональной ковариационной матрицей.  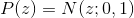— одномерное нормальное латентное представление.

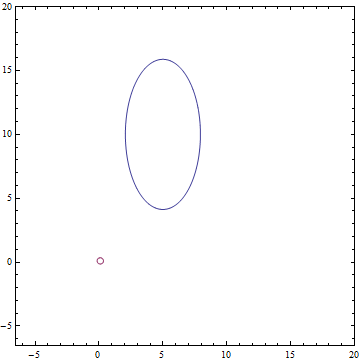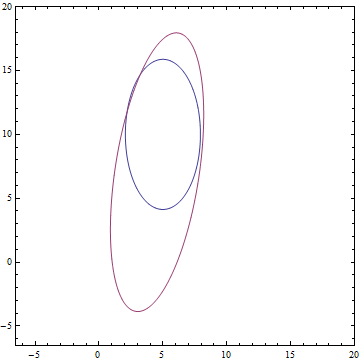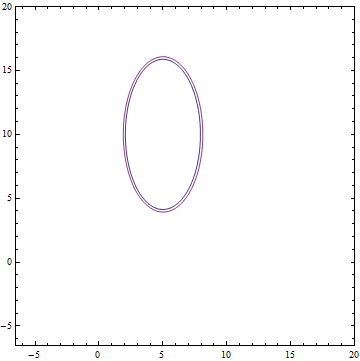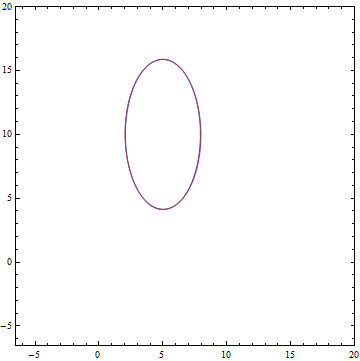
Рис. 1. Эллипс вокруг среднего, в который попадает 95% точек из распределения .

Итак, первое, что нужно сделать — это сгенерировать данные. Мы генерируем сэмплы из :

def normal_samples(batch_size):
  def example():
    return tf.contrib.distributions.MultivariateNormalDiag(
     [5, 10], [1.2, 2.4]).sample(sample_shape=[1])[0]
  return tf.contrib.data.Dataset.from_tensors([0.])
    .repeat()
    .map(lambda x: example())
    .batch(batch_size)

Теперь нужно определить параметры модели:

input_size = 2
latent_space_size = 1
stddev = tf.get_variable(
  "stddev", initializer=tf.constant(0.1, shape=[1]))
biases = tf.get_variable(
  "biases", initializer=tf.constant(0.1, shape=[input_size]))
weights = tf.get_variable(
  "Weights",
   initializer=tf.truncated_normal(
     [input_size, latent_space_size], stddev=0.1))

После этого можно получить для сэмпла видимых переменных их латентные представления:

def get_latent(visible, latent_space_size, batch_size):
  matrix = tf.matrix_inverse(
    tf.matmul(weights, weights, transpose_a=True)
      + stddev**2 * tf.eye(latent_space_size))
  mean_matrix = tf.matmul(matrix, weights, transpose_b=True)
  # Multiply each vector in a batch by a matrix.
  expected_latent = batch_matmul(
    mean_matrix, visible - biases, batch_size)
  stddev_matrix = stddev**2 * matrix
  noise =
    tf.contrib.distributions.MultivariateNormalFullCovariance(
      tf.zeros(latent_space_size),
      stddev_matrix)
        .sample(sample_shape=[batch_size])
  return tf.stop_gradient(expected_latent + noise)

Тут нужно обратить внимание на tf.stop_gradient (…). Эта функция не дает значениям параметров внутри входного подграфа влиять на градиент по этим параметрам. Это нужно, чтобы 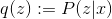оставалось фиксированным в течении M-шага, что необходимо для корректной работы EM-алгоритма.

Давайте теперь запишем функцию потерь 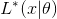для оптимизации на M-шаге:

sample = dataset.get_next()
latent_sample = get_latent(sample, latent_space_size, batch_size)
norm_squared = tf.reduce_sum((sample - biases -
  batch_matmul(weights, latent_sample, batch_size))**2, axis=1)
loss = tf.reduce_mean(
  input_size * tf.log(stddev**2) + 1/stddev**2 * norm_squared)
train = tf.train.AdamOptimizer(learning_rate)
  .minimize(loss, var_list=[bias, weights, stddev], name="train")

Итак, модель готова для тренировки. Давайте взглянем на кривую обучения модели:

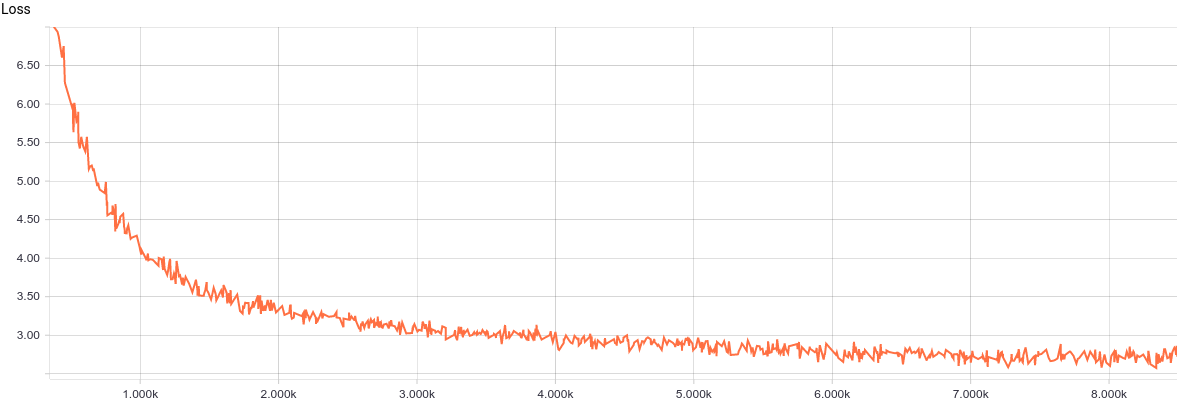
Рис. 2. Кривая обучения модели PPCA.

Видно, что модель достаточно регулярно и быстро сходится, что хорошо отражает простоту модели. Давайте посмотрим на выученные параметры распределения.

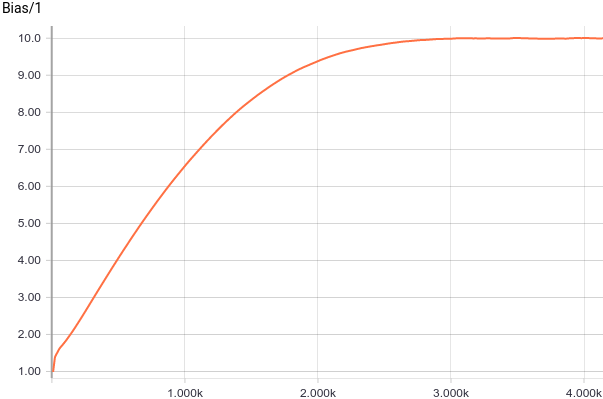
Рис. 3. Графики смещения от начала координат (параметра ).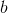

Видно, что 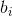 быстро сошлись к аналитическим значениям 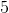и . Давайте теперь посмотрим на параметры :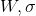

Рис. 4. График изменения параметра .

Видно, что значение сошлось к 1.2, т.е. к меньшей оси отклонения входного распределения, как и ожидалось.

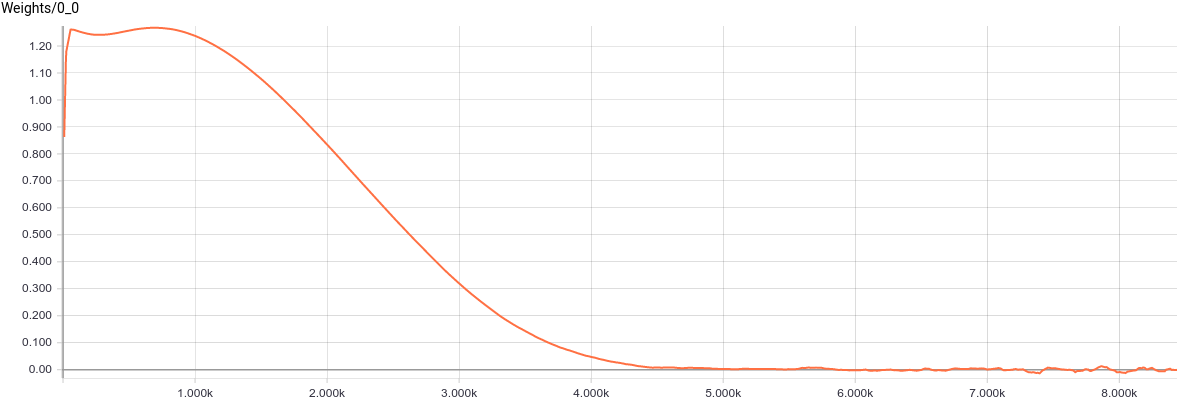
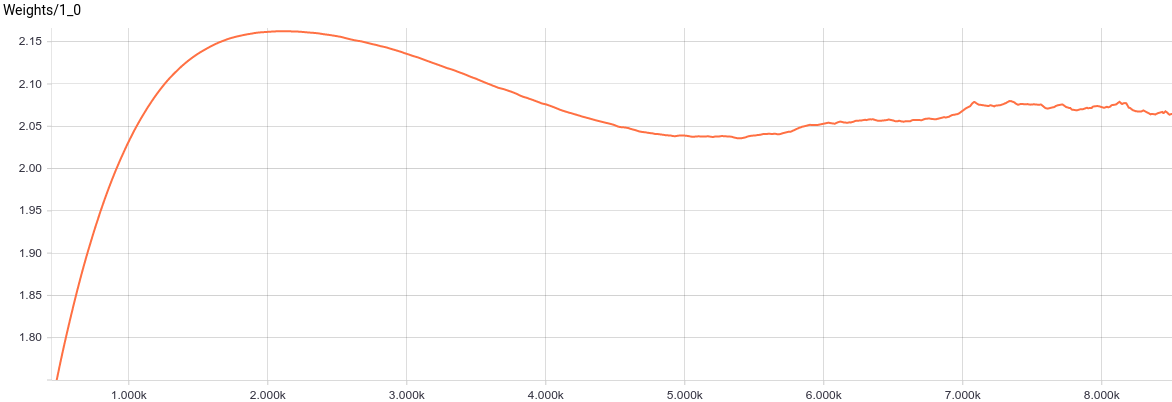
Рис. 5. Графики изменения параметров .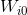

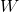, в свою очередь, сошлось к примерно такому значению, при котором 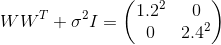. Подставляя эти значения в модель, мы получаем 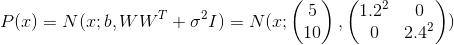, что значит, что мы восстановили распределение данных.

Давайте посмотрим на распределения данных. Латентная переменная одномерна, потому она отображена как одномерное распределение. Видимая переменная же двумерна, но ее заданная матрица ковариации диагональна, что значит, что ее эллипсоид выровнен с осями координат. Потому мы отобразим ее как две проекции ее распределения на оси координат. Так выглядят заданное и выученное распределение в проекции на первую ось координат:

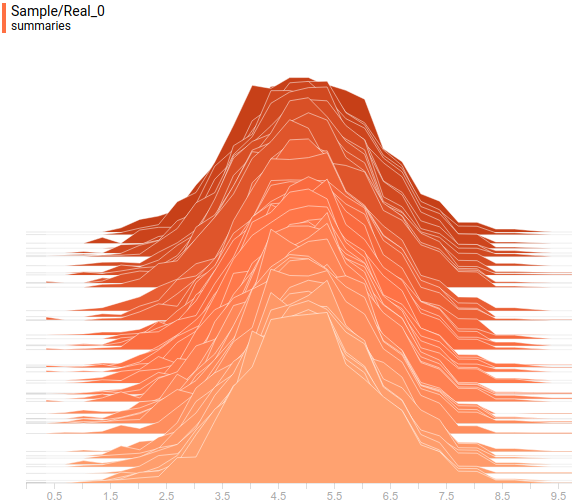
Рис. 6. Проекция заданного распределения на первую ось координат.

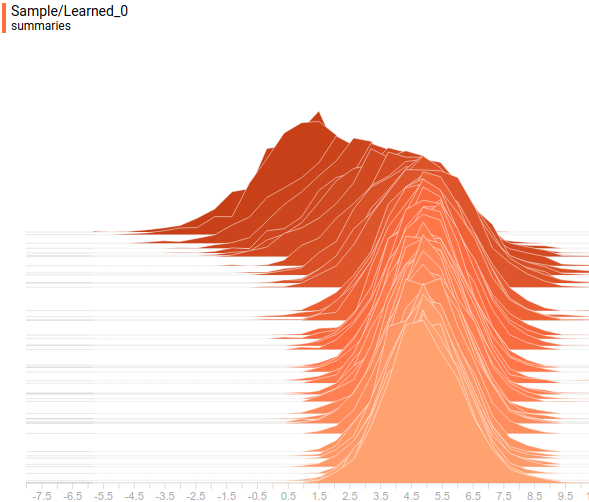
Рис. 7. Проекция выученного распределения 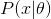на первую ось координат.

А так выглядят заданное и выученное распределение в проекции на вторую ось координат:

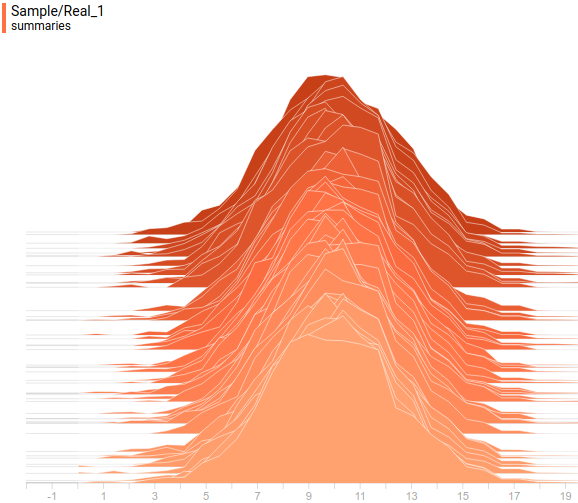
Рис. 8. Проекция заданного распределения на вторую ось координат.

Рис. 9. Проекция выученного распределения на вторую ось координат.

А так выглядят аналитическое и выученное распределения :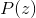

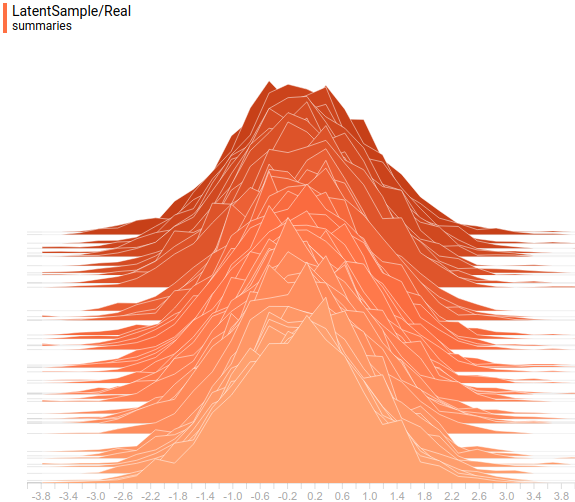
Рис. 10. Заданное распределение .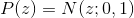

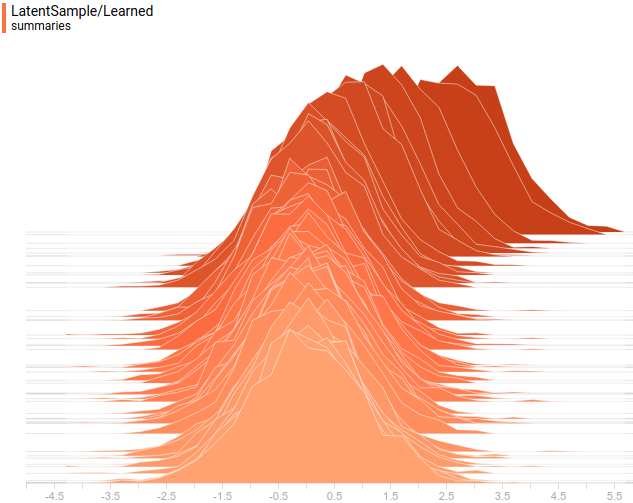
Рис. 11. Выученное распределение .

Видно, что все выученные распределения сходятся к распределениям, очень похожим на заданные задачей. Давайте посмотрим на динамику обучения модели, чтобы убедиться в этом окончательно:

Рис. 12. Процесс обучения модели PPCA, при котором выученное распределение сходится к распределению данных .

Заключение

Приведенная модель — это вероятностная интерпретация классической модели PCA, которая является линейной моделью. Мы использовали математику из оригинальной статьи, построили GEM алгоритм поверх нее и показали, что получившаяся модель сходится к аналитическому решению на простом примере. Разумеется, если бы в задаче не было нормальным, модель бы не справилась так хорошо. Точно так же, как PCA не справляется идеально с данными, не лежащими в некой гиперплоскости. Для решения более сложных задач аппроксимации распределений нам понадобятся более сложные и нелинейные модели. Об одной из таких моделей, Generative Adversarial Networks, и пойдет речь в следующей статье.

Благодарности

Спасибо Olga Talanova за ревью текста. Спасибо Andrei Tarashkevich за помощь с версткой этой статьи.

© Habrahabr.ru