[Перевод] Как развивалось восприятие пространства человеком, и зачем нам нужны измерения
Теория относительности утверждает, что мы живём в четырёх измерениях. Теория струн — что в десяти. Что такое «измерения» и как они влияют на реальность?

Когда я пишу тексты за своим столом, я могу протянуть руку вверх, чтобы включить лампу, или вниз, чтобы открыть ящик стола и достать ручку. Протянув руку вперёд, я касаюсь небольшой и странной на вид статуэтки, которую мне на счастье подарила сестра. Потянувшись назад, я могу похлопать чёрную кошку, крадущуюся у меня за спиной. Справа лежат заметки, сделанные во время исследований для статьи, слева — куча вещей, которые необходимо сделать (счета и корреспонденция). Вверх, вниз, вперёд, назад, вправо, влево — я управляю самим собой в моём личном космосе трёхмерного пространства. Невидимые оси этого мира налагает на меня прямоугольная структура моего кабинета, определяемая, как и большая часть западной архитектуры, тремя составленными вместе прямыми углами.
Наши архитектура, образование и словари сообщают нам о трёхмерности пространства. Оксфордский словарь английского языка так определяет пространство: «непрерывная область или простор, свободная, доступная или не занятое ничем. Измерения высоты, глубины и ширины, в рамках которых существуют и движутся все вещи». [словарь Ожегова говорит похожим образом: «Протяженность, место, не ограниченное видимыми пределами. Промежуток между чем-н., место, где что-н. вмещается.» / прим. перев.]. В XVIII веке Иммануил Кант утверждал, что трёхмерное евклидово пространство является априорной необходимостью, и нам, пресыщенным изображениями, созданными компьютером, и видеоиграми, постоянно напоминают об этом представлении в виде вроде бы аксиоматичной прямоугольной системы координат. В точки зрения XXI века это кажется уже почти самоочевидным.
И всё же идея о жизни в пространстве, описываемом какой-то математической структурой — это радикальная инновация западной культуры, сделавшая необходимостью опровержение старинных верований по поводу природы реальности. Хотя зарождение современной науки часто описывают как переход к механизированному описанию природы, вероятно, более важным его аспектом — и однозначно более длительным — был переход к понятию о пространстве как о геометрической конструкции.
В прошлом веке задача описания геометрии пространства стала основным проектом теоретической физики, в котором эксперты, начиная с Альберта Эйнштейна, пытались описать все фундаментальные взаимодействия природы в виде побочных продуктов формы самого пространства. Хотя на локальном уровне нас приучили думать о пространстве как о трёхмерном, общая теория относительности описывает четырёхмерную Вселенную, а теория струн говорит о десяти измерениях — или об 11, если взять за основу её расширенный вариант, М-теорию. Существуют варианты этой теории с 26-ю измерениями, а недавно математики с энтузиазмом приняли версию, описывающую 24 измерения. Но что это за «измерения»? И что означает наличие десяти измерений в пространстве?
Чтобы прийти к современному математическому пониманию пространства, сначала необходимо подумать о нём как о некоей арене, которую может занимать материя. По меньшей мере, пространство необходимо представить себе, как нечто протяжённое. Такая идея, пусть и очевидная для нас, показалась бы еретической Аристотелю, чьи концепции представления физического мира преобладали в западном мышлении в поздней античности и в средневековье.
Строго говоря, аристотелева физика включала в себя не теорию пространства, а лишь концепцию места. Рассмотрим чашку чаю, стоящую на столе. Для Аристотеля чашка была окружённой воздухом, самим по себе представлявшим некую субстанцию. В его картине мира не было такой вещи, как пустое пространство — были только границы между веществами — чашкой и воздухом. Или столом. Для Аристотеля пространство, если вы хотите его так называть, было лишь бесконечно тонкой гранью между чашкой и тем, что её окружает. Баз протяжённости пространство не было чем-то таким, внутри чего может быть что-то другое.
За столетие до Аристотеля Левкипп и Демокрит предложили теорию реальности со способом наблюдения, сильно завязанным на пространство — атомистическое видение, в котором материальный мир состоит из крошечных частиц, или атомов, движущихся в пустоте. Но Аристотель отверг атомизм, заявляя, что сама концепция пустоты логически противоречива. Он сказал, что определению «ничто» существовать не может. Проект опровержения возражений Аристотеля против пустоты и концепции протяжённого пространства займёт столетия. Только когда Галилей и Декарт сделали протяжённое пространство одним из краеугольных камней современной физики в XVII веке, этот инновационный подход обрёл права на существование. Для обоих мыслителей, как сказал в 1924 году американский философ Эдвин Бёрт, «физическое пространство предполагалось идентичным геометрическому», — то есть, трёхмерной евклидовой геометрии, которую сейчас проходят в школах.
Задолго до того, как физики приняли точку зрения Евклида, художники открывали геометрические концепции пространства, и именно им мы обязаны выдающимся скачком в развитии нашей концептуальной платформы. В позднем средневековье под влиянием новых идей, основывающихся на работах Платона и Пифагора, интеллектуальных соперников Аристотеля, в Европе начали распространяться взгляды, согласно которым Бог создал этот мир в соответствии с законами евклидовой геометрии. Поэтому, если художник хотел запечатлеть его истинный вид, ему нужно было эмулировать работу Творца в своей репрезентации. С XIV по XVI век такие художники, как Джотто ди Бондоне, Паоло Уччелло и Пьеро делла Франческа разработали техники использования того, что позднее стало называться перспективой — стиль, изначально названный «геометрическим изображением». Сознательно изучая геометрические принципы, эти художники постепенно учились тому, как создавать изображения объектов трёхмерного пространства. В процессе они перепрограммировали европейские умы на то, чтобы видеть пространство по-евклидовому.
Историк Сэмюэл Эдгертон подробно описывает этот замечательный и плавный переход к современной науке в книге «Наследие геометрии Джотто» [The Heritage of Giotto«s Geometry (1991)], отмечая, как отказ от Аристотелева мышления о пространстве произошёл в частности благодаря длительному процессу, являющемуся побочным продуктом наблюдения людьми за картинами, сделанными в перспективе, и их интуитивного ощущения того, что они как бы «заглядывают» в трёхмерные миры по другую сторону стены. Необычность этого состоит в том, что пока философы и предшественники учёных осторожно пытались спорить с Аристотелевым восприятием пространства, художники прорубали себе путь по этой интеллектуальной территории, апеллируя к ощущениям. Совершенно буквально перспективное изображение было разновидностью виртуальной реальности, которая, на манер современных VR-игр, была направлена на создание у зрителя иллюзии перемещения в геометрически непротиворечивые и психологически убедительные иные миры.
Иллюзорное евклидово пространство перспективного изображения, постепенно откладывавшееся в сознании европейцев, было принято Декартом и Галилеем, как пространство реального мира. Стоит отметить, что сам Галилей имел опыт обращения с перспективой. Его способность изображения глубины стала критически важной в его прорывных изображениях Луны, на которых были показаны горы и долины, и которые говорили о том, что Луна состоит из такого же твёрдого материала, что и Земля.
Приняв пространство перспективных изображений, Галилей смог показать, как такие объекты, как пушечные ядра, движутся согласно законам математики. Пространство само по себе было абстракцией: непримечательной, инертной, неосязаемой пустотой, чьим единственным известным свойством была евклидова форма. К концу XVII века Исаак Ньютон расширил видение Галилея, чтобы объять всю Вселенную целиком, и сейчас эта идея превратилась в потенциально бесконечный трёхмерный вакуум — протяжённую, лишённую особенностей пустоту, вечно длящуюся во всех направлениях. Структура реальности таким образом превратилась из философского и теологического вопроса в геометрическое предложение.
Пока художники использовали математические инструменты для выработки новых способов создания изображений, Декарт на заре научной революции открыл способ создания изображений математических взаимосвязей. В процессе он формализовал концепцию измерения и ввёл в наше сознание не только новый способ смотреть на мир, но и новый метод заниматься наукой.
Сегодня практически все признают плоды гения Декарта в виде прямоугольной системы координат — решётки на плоскости, размеченной осями x и у.
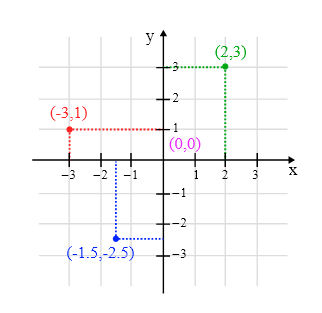
По определению, плоскость декартовых координаты — двумерная, поскольку для определения любой точки на ней нам требуется две координаты. Декарт обнаружил, что на такой платформе можно связывать геометрические формы и уравнения. Таким способом круг радиуса 1 можно описать в виде уравнения x2 + y2 = 1
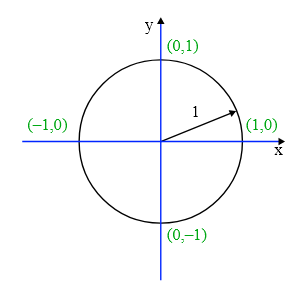
Огромный набор форм, которые мо можем нарисовать на этой плоскости, можно описать уравнениями — и такая «аналитическая геометрия» вскоре станет основой для математического анализа, разработанного Ньютоном и Лейбницем для анализа движения физиками. Один из способов понять матан — изучать кривые. Он, к примеру, позволяет нам формально определить место, где у кривой имеется наибольший наклон, или где она достигает локального максимума или минимума. В применении к изучению движения матан даёт нам способ анализировать и предсказывать где, к примеру, объект, брошенный в воздух, достигнет максимальной высоты, или где шар, катящийся вниз по искривлённому склону, достигнет определённой скорости. С момента изобретения матан стал жизненно важным инструментом почти для всех областей науки.
На примере последней диаграммы легко видеть, как можно добавить третье измерение. При помощи осей x, y и z мы можем описать поверхность сферы — к примеру, поверхность пляжного меча. Уравнение для сферы радиуса 1 приобретает вид x2 + y2 + z2 = 1
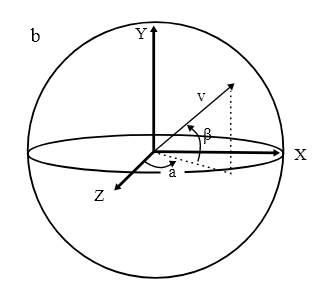
При помощи трёх осей можно описывать формы в трёхмерном пространстве. Опять-таки, каждая точка уникальным образом определяется тремя координатами — это необходимое условие тройственности, делающее пространство трёхмерным.
Но к чему останавливаться на этом? Что, если добавить четвёртое измерение? Назовём его «p». Теперь я могу записать уравнение для того, что я назову сферой, находящейся в четырёхмерном пространстве: x2 + y2 + z2 + p2 = 1. Нарисовать я её не могу, однако с математической точки зрения добавить дополнительное измерение можно. «Можно» означает, что в этом действии нет ничего логически противоречивого.
И я могу продолжать заниматься этим и далее, добавляя дополнительные измерения. Сферу в пятимерном пространстве с осями (x, y, z, p, q) я могу определить уравнением: x2 + y2 + z2+ p2 + q2 = 1. А в шестимерном: x2 + y2 + z2 + p2 + q2 + r2 = 1, и так далее.
Может, я и не могу изобразить сферы из высших измерений, зато я могу описать их символически, и один из способов понимания истории математики — постепенно приходящее осознание того, за пределы каких вроде бы разумных вещей мы можем выйти. Именно это Чарльз Лютвидж Доджсон, он же Льюис Кэрролл, имел в виду в романе «Сквозь зеркало, и Что там нашла Алиса» (1871), когда Белая Королева утверждала, что способна «поверить в шесть невозможных вещей ещё до завтрака».
Математически я могу описать сферу в любом количестве измерений, в котором захочу. Мне просто нужно добавлять новые координатные оси, то, что математики называют «степенями свободы». Обычно они обозначаются, как x1, x2, x3, x4, x5, x6, и так далее. Так же, как любую точку декартовой плоскости можно описать двумя координатами (x, y), любую точку 17-мерного пространства можно описать набором из 17 координат (x1, x2, x3, x4, x5, x6, … x15, x16, x17). Поверхности типа описанной выше сферы в многомерных пространствах называют многообразиями.
С математической точки зрения, «измерение» — это всего лишь ещё одна координатная ось, ещё одна степень свободы, становящаяся символической концепцией, не обязательно связанной с материальным миром. В 1860-х пионер в области логики Огастес де Морган, чьи работы повлияли на Льюиса Кэрролла, подытожил эту становящуюся всё более абстрактной область, отметив, что математика — это чисто «наука о символах», и как таковая не обязана связываться с чем-либо, кроме самой себя. Математика, в каком-то смысле, это логика, свободно перемещающаяся на полях воображения.
В отличие от математиков, свободно играющих на полях идей, физики привязаны к природе, и, по крайней мере, в принципе, зависят от материальных вещей. Но все эти идеи приводят нас к освобождающей возможности — ведь если математика допускает количество измерений больше трёх, и мы считаем, что математика оказывается полезной для описания мира, откуда нам знать, что физическое пространство ограничено тремя измерениями? Хотя Галилей, Ньютон и Кант принимали длину, ширину и высоту как аксиомы, не может ли в нашем мире существовать больше измерений?
Опять-таки, идея Вселенной с количеством измерений больше трёх проникла в сознание общества через художественную среду, на этот раз — через литературные рассуждения, наиболее известной из которых служит работа математика Эдвина Эбботта Эбботта «Флатландия» (1884). Это очаровательная социальная сатира рассказывает историю скромного Квадрата, живущего на плоскости, к которому однажды в гости приходит трёхмерное существо лорд Сфера, выводящее его в великолепный мир трёхмерных тел. В этом рае объёмов Квадрат наблюдает за его трёхмерной версией, Кубом, и начинает мечтать о переходе в четвёртое, пятое и шестое измерение. Почему не гиперкуб? Или не гипер-гиперкуб, думает он?
К сожалению, в Флатландии Квадрата причисляют к лунатикам и запирают в сумасшедший дом. Одной из моралей истории, в отличие от более слащавых её экранизаций и адаптаций, является опасность, таящаяся в игнорировании социальных устоев. Квадрат, рассказывая о других измерениях пространства, рассказывает и о других изменениях бытия — он становится математическим чудаком.
В конце XIX и начале XX веков масса авторов (Герберт Уэллс, математик и автор НФ-романов Чарльз Хинтон, придумавший слово «тессеракт» для обозначения четырёхмерного куба), художников (Сальвадор Дали) и мистиков (Пётр Демьянович Успенский [русский оккультист, философ, теософ, таролог, журналист и писатель, математик по образованию / прим. перев.] изучала идеи, связанные с четвёртым измерением и тем, чем может стать для человека встреча с ним.
Затем в 1905 году неизвестный тогда физик Альберт Эйнштейн опубликовал работу, описывающую реальный мир как четырёхмерный. В его «специальной теории относительности» время добавлялось к трём классическим измерениям пространства. В математическом формализме относительности все четыре измерения связаны вместе — так в наш лексикон вошёл термин «пространство-время». Такое объединение было не произвольным. Эйнштейн обнаружил, что используя этот подход, можно создать мощный математический аппарат, превосходящий физику Ньютона и позволяющий ему предсказывать поведение электрически заряженных частиц. Электромагнетизм можно полностью и точно описать только в четырёхмерной модели мира.
Относительность стала чем-то гораздо большим, чем просто ещё одной литературной игрой, особенно когда Эйнштейн расширил её от «специальной» до «общей». Многомерное пространство приобрело глубинное физическое значение.
В картине мира Ньютона материя движется через пространство во времени под влиянием естественных сил, в частности, гравитации. Пространство, время, материя и силы — различные категории реальности. С СТО Эйнштейн демонстрировал объединение пространства и времени, уменьшая количество фундаментальных физических категорий с четырёх до трёх: пространства-времени, материи и сил. ОТО делает следующий шаг, вплетая гравитацию в структуру самого пространства-времени. С четырёхмерной точки зрения, гравитация — всего лишь артефакт формы пространства.
Чтобы осознать эту примечательную ситуацию, представим её двумерный аналог. Представьте себе батут, нарисованный на поверхности декартовой плоскости. Теперь разместим на решётке шар для боулинга. Вокруг него поверхность натянется и исказится так, что некоторые точки отдалятся друг от друга сильнее. Мы исказили внутреннюю меру расстояния в пространстве, сделали её неровной. ОТО говорит, что именно такому искажению тяжёлые объекты, такие, как Солнце, подвергают пространство-время, и отклонение от декартового совершенства пространства приводит к появлению явления, которое мы ощущаем, как гравитацию.
В физике Ньютона гравитация появляется из ниоткуда, а у Эйнштейна она естественным образом возникает из внутренней геометрии четырёхмерного многообразия. Там, где многообразие наибольшим образом растягивается, или отходит от декартовой регулярности, гравитация ощущается сильнее. Это иногда называют «физикой резиновой плёнки». В ней огромные космические силы, удерживающие планеты на орбитах вокруг звёзд, а звёзды на орбитах в рамках галактик, являются ничем иным, как побочным эффектом искажённого пространства. Гравитация — это буквально геометрия в действии.
Если переход в четырёхмерное пространство помогает объяснить гравитацию, то будет ли какое-либо научное преимущество у пятимерного пространства? «Почему бы не попробовать?» — спросил в 1919 году молодой польский математик Теодор Франц Эдуард Калуца, размышляя над тем, что если Эйнштейн включил гравитацию в пространство-время, то, возможно, дополнительное измерение может схожим образом обращаться с электромагнетизмом, как с артефактом геометрии пространства-времени. Поэтому Калуца добавил дополнительное измерение к уравнениям Эйнштейна, и, к своему восторгу, обнаружил, что в пяти измерениях обе эти силы прекрасно оказываются артефактами геометрической модели.
Математика волшебным образом сходится, но в данном случае проблемой стало то, что дополнительное измерение никак не коррелировало с каким-либо определённым физическим свойством. В ОТО четвёртым измерением было время; в теории Калуцы оно не было чем-либо, что можно увидеть, почувствовать или на что можно указать: оно просто было в математике. Даже Эйнштейн разочаровался в такой эфемерной инновации. Что это? — спрашивал он; где оно?
В 1926 году шведский физик Оскар Клейн дал на этот вопрос ответ, очень похожий на отрывок из произведения о Стране чудес. Он предложил представить себе муравья, живущего на очень длинной и тонкой секции шланга. По шлангу можно бегать вперёд и назад, даже не замечая крохотного кругового изменения под ногами. Это измерение смогут увидеть только муравьиные физики при помощи мощных муравьиных микроскопов. Согласно Клейну, каждая точка нашего четырёхмерного пространства-времени обладает небольшим дополнительным кружком в пространстве подобного рода, который слишком мал для того, чтобы мы его видели. Поскольку он во много раз меньше атома, неудивительно, что мы его пока не нашли. Только физики с очень мощными ускорителями частиц могут надеяться добраться до такой крохотной шкалы.
Когда физики отошли от первоначального шока, идея Клейна их покорила, и в течение 1940-х эта теория была разработана в больших математических подробностях и перенесена в квантовый контекст. К несчастью, бесконечно малая шкала нового измерения не даёт представить, как его существование можно подтвердить экспериментально. Клейн подсчитал, что диаметр крохотного кружка составляет примерно 10–30 см. Для сравнения, диаметр атома водорода равен 10–8 см, поэтому мы говорим о чём-то, на 20 порядков меньшем, чем самый мелкий из атомов. Даже сегодня мы вовсе не приблизились к тому, чтобы суметь разглядеть что-то на такой миниатюрной шкале. Так эта идея вышла из моды.
Калуцу же так просто было не напугать. Он верил в своё пятое измерение и в мощь математической теории, поэтому он решил провести собственный эксперимент. Он выбрал такую тему, как плавание. Он не умел плавать, поэтому он прочёл всё, что нашёл, по теории плавания, и когда решил, что достаточно полно овладел принципами поведения на воде, поехал с семьёй к морю, бросился в волны, и внезапно поплыл. С его точки зрения эксперимент по плаванию подтверждал правдивость его теории, и, хотя он не дожил до триумфа своего любимого пятого измерения, в 1960-х специалисты по теории струн возродили идею пространства с высшими измерениями.
К 1960-м физики открыли две дополнительных силы природы, работающие на субатомном масштабе. Их назвали слабым ядерным взаимодействием и сильным ядерным взаимодействием, и они отвечают за некоторые типы радиоактивности и за удержание кварков, формирующих протоны и нейтроны, из которых состоят атомные ядра. В концце 1960-х физики начали изучать новую тему теории струн (утверждающей, что частицы похожи на крохотные резиновые полоски, вибрирующие в пространстве), и идеи Калуцы и Клейна вновь вышли на поверхность. Теоретики начали постепенно приходить к мысли, нельзя ли описать две субатомные силы в терминах геометрии пространства-времени.
Оказывается, что для того, чтобы охватить обе эти силы, необходимо добавить ещё пять измерений к нашему математическому описанию. Не существует какой-то особой причины для того, чтобы их было пять; и вновь, никакие из этих дополнительных измерений не связаны с нашими ощущениями напрямую. Они есть только в математике. И это приводит нас к 10 измерениям теории струн. И вот вам четыре крупномасштабных измерения пространства-времени (описываемые ОТО), плюс шесть дополнительных «компактных» измерений (одно для электромагнетизма и пять для ядерных сил), свернувшиеся клубочком в чертовски сложную, сморщенную геометрическую структуру.
Физики и математики прилагают огромные усилия к тому, чтобы понять все возможные формы, которые способно принять это миниатюрное пространство, и какие, если вообще какие-то из множества этих альтернатив, реализуются в реальном мире. Технически эти формы известны как многообразия Калаби-Яу, и они могут существовать в любом количестве высших измерений. Эти экзотические и сложные существа, эти необычайные формы, составляют абстрактную систематику в многомерном пространстве; их двумерное сечение (лучшее, что мы можем сделать для визуализации их внешнего вида) напоминает кристаллические структуры вирусов; они кажутся почти живыми.

Существует множество версий уравнений теории струн, описывающих десятимерное пространство, но в 1990-х математик Эдвард Виттен из Института передовых исследований в Принстоне (старого логова Эйнштейна) показал, что всё можно немного упростить, если перейти к 11-мерной перспективе. Он назвал свою новую теорию «М-теория», и загадочно отказался объяснить, что обозначает буква «М». Обычно говорят, что она обозначает «мембрану», но кроме этого поступали и такие предложения, как «матрица», «мастер», «мистическая» и «монструозная».
Пока что у нас нет никаких свидетельств этих дополнительных измерений — мы всё ещё находимся в состоянии плавающих физиков, мечтающих о недоступных миниатюрных ландшафтах —, но теория струн оказала мощное влияние на саму математику. Недавно разработки версии этой теории, имеющей 24 измерения, показали наличие неожиданной взаимосвязи между несколькими основными ответвлениями математики, что означает, что даже если теория струн не пригодится в физике, она станет полезным источником чисто теоретических идей. В математике 24-мерное пространство особенное — там происходят волшебные вещи, к примеру, возможно упаковать сферы особенно элегантным образом — хотя маловероятно, что в реальном мире 24 измерения. Касательно мира, в котором мы живём и который мы любим, большинство специалистов по теории струн считают, что 10 или 11 измерений будет достаточно.
Внимания достойно ещё одно событие теории струн. В 1999 году Лиза Рэндалл (первая женщина, получившая пост в Гарварде в области теоретической физики) и Раман Сандрум (американский специалист по теоретической физике частиц индийского происхождения) предположили, что дополнительное измерение может существовать на космологической шкале, на масштабах, описываемых теорией относительности. Согласно их теории «бран» (брана — это сокращение от мембраны) — то, что мы называем нашей Вселенной, может находиться в гораздо более крупном пятимерном пространстве, в чём-то вроде сверхвселенной. В этом сверхпространстве наша Вселенная может быть одной из целого ряда существующих вместе вселенных, каждая из которых представляет собой четырёхмерный пузырь на более широкой арене пятимерного пространства.
Сложно сказать, сможем ли мы когда-нибудь подтвердить теорию Рэндалл и Сандрума. Однако между этой идеей и зарёй современной астрономии уже проводят некоторые аналогии. 500 лет назад европейцы считали невозможным представить себе иные физические «миры» кроме нашего собственного, однако сейчас нам известно, что Вселенная заполнена миллиардами других планет, движущихся по орбитам вокруг миллиардов других звёзд. Кто знает, может когда-нибудь наши потомки смогут найти доказательства существования миллиардов других вселенных, у каждой из которых есть свои уникальные уравнения для пространства-времени.
Проект понимания геометрической структуры пространства — одно из характерных достижений науки, но может получиться так, что физики достигли конца этого пути. Оказывается, что Аристотель в каком-то смысле был прав — у идеи протяжённого пространства и правда есть логические проблемы. Несмотря на все необычайные успехи теории относительности, мы знаем, что её описание пространства не может быть итоговым, поскольку оно отказывает на квантовом уровне. За последние полвека физики безуспешно пытались объединить их понимание пространства на космологическом масштабе с тем, что они наблюдают на квантовом масштабе, и всё больше кажется, что такой синтез может потребовать радикально новой физики.
Эйнштейн после разработки ОТО провёл большую часть жизни, пытаясь «выразить все законы природы из динамики пространства и времени, низведя физику к чистой геометрии», как сказал недавно Робберт Дийкграаф [Robbert Dijkgraaf], директор Института передовых исследований в Принстоне. «Для Эйнштейна пространство-время было естественным фундаментом бесконечной иерархии научных объектов». Как и у Ньютона, картина мира Эйнштейна ставит пространство во главу существование, делает его ареной, на которой всё происходит. Но на крохотных масштабах, где преобладают квантовые свойства, законы физики показывают, что такого пространства, к которому мы привыкли, может и не быть.
Некоторые физики-теоретики начинают высказывать мысль о том, что пространство может быть некоим возникающим явлением, следующим из чего-то более фундаментального, так, как температура возникает на макроскопическом масштабе в результате движения молекул. Как говорит Дийкграаф: «Текущая точка зрения считает пространство-время не точкой отсчёта, а итоговой финишной чертой, естественной структурой, появляющейся из сложности квантовой информации».
Ведущий сторонник новых способов представления пространства — космолог Шон Кэрролл из Калтеха, сказавший недавно, что классическое пространство — это не «фундаментальная часть архитектуры реальности», и доказывающей, что мы неверно присваиваем такой особый статус его четырём, или 10, или 11 измерениям. Если Дийкграаф приводит аналогию с температурой, то Кэрролл предлагает нам рассмотреть «влажность», явление, проявляющееся оттого, что множество молекул воды собираются вместе. Отдельные молекулы воды не являются влажными, и свойство влажности появляется только тогда, когда вы соберёте множество их в одном месте. Точно так же, говорит он, пространство появляется из более базовых вещей на квантовом уровне.
Кэрролл пишет, что с квантовой точки зрения Вселенная «появляется в математическом мире с количеством измерений порядка 1010100» — это десятка с гуголом нулей, или 10 000 и ещё триллион триллионов триллионов триллионов триллионов триллионов триллионов триллионов нулей. Сложно представить такое невозможно огромное количество, по сравнению с которым количество частиц во Вселенной оказывается совершенно незначительным. И всё же, каждое из них — отдельное измерение в математическом пространстве, описываемое квантовыми уравнениями; каждое — это новая «степень свободы», имеющаяся в наличии у Вселенной.
Даже Декарт был бы поражён тем, куда нас завели его рассуждения, и какая удивительная сложность скрывалась в таком простом слове, как «измерение».
