Где порешать аналитические задачи от команд Яндекса? Контест и разбор21.09.2020 18:03

На каждом шаге вероятность получить ответ «Да, я лгун» складывается из вероятности получить ответ «Да»:

— От правдолюбов, которых не спрашивали до этого: 0,2 * доля правдолюбов, которых не спрашивали.
— От лгунов, которых не спрашивали до этого: 0,4 * доля лгунов, которых не спрашивали.
— От правдолюбов, которых уже спрашивали до этого и которые ответили «Да»: 1,0 * доля правдолюбов, которых уже спрашивали и которые ответили «Да».
— От лгунов, которых уже спрашивали до этого и которые ответили «Да»: 1,0 * доля лгунов, которых уже спрашивали и которые ответили «Да».

Посчитаем по шагам вероятность получить ответ «Да» от правдолюбов:

1. 0,2 * % правдолюбов.
2. 0,2 * (% правдолюбов — % опрошенных правдолюбов) + 0,2 * (% опрошенных правдолюбов) = 0,2 * % правдолюбов.
3. Аналогично шагу 2.

То есть на каждом шаге вероятность получить ответ «Да, я лгун» от правдолюбов составляет 0,2 и не зависит от того, сколько правдолюбов опросили до этого. Точно так же для лгунов.

Таким образом, вероятность получить ответ «Да» от правдолюбов и лгунов: 0,2×0,7 + 0,4×0,3 = 0,26.

2. Посчитаем вероятность недооценить количество лгунов.

Количество лгунов, которое получит государство по результатам опроса, — это биномиальное распределение с параметрами n = 100, p = 0,26.

Количеством «успехов» в нашем случае будет 30 (30% от 100 опрошенных). Если мы посмотрим на функцию распределения в этой точке, то получим P (x < 30) = 0,789458. Посчитать можно вот тут: stattrek.com/online-calculator/binomial.aspx.

Ответ в процентах, округлённых до сотых: 78,95.

Подробный вариант решения лежит в main.py.

Пользователи оставляют телефонные номера в разных форматах. В качестве набора данных берутся случайно сгенерированные номера из необслуживаемых кодов. По данным из Википедии были взяты необслуживаемые зоны 801–807.

Каждый номер может получить одного и более двойников из следующих вариантов:

1. 8-(801)-111–11–11
2. 8–801–111–11–11
3. 8801–111–11–11
4. 8–8011111111
5. +88011111111
6. 8–801-flowers, вместо цифр — буквы (распространено в США)

Как предполагается обнаружить эти особенности:

1. Форматы в пунктах 1–4 видны при первом взгляде на данные и удаляются стандартными методами вроде replace.
2. Формат 5 легко отфильтровать, проверив число символов в телефонах после форматирования пункта 1. Во всех номерах будет 11 символов, кроме этого формата.
3. Пункт 6 самый неочевидный, надо догадаться проверить наличие нечисловых символов в номере телефона. Надеюсь, что смысл этих букв участник быстро найдёт в интернете.

Количество данных относительно небольшое, чтобы при желании можно было даже просмотреть каждую строчку вручную. Найти все шесть форматов можно вообще в первой сотне строк.

Код. Как генерировались данные

Этот раздел для тех, кому надо разобраться в устройстве кода или изменить сгенерированные логи в ticket_logs.csv. Все действия сложены в logs_generator.py. Как запустить:

python logs_generator.py

На выходе получается файл ticket_logs.csv.

Конфигурационный файл config.yaml

В файле собраны все параметры, которые влияют на создание файла ticket_logs.csv:

• zones — коды зон, которые используются в генерируемых телефонных номерах.
• seven_letter_words — слова, которые используются для создания телефонных номеров с буквами.
• letters_to_numbers_dict — словарь соответствия цифр на клавиатуре телефона и алфавита. Вряд ли он изменится.
• performances — список спектаклей и их весов. Чем выше вес, тем чаще спектакль будет в логах ticket_logs.csv.

USERS_COUNT = 1000  # количество пользователей (можно сверять в решении main.py результат)
RESULT_FILE_LOCATION = 'ticket_logs.csv'  # куда сохранять созданные логи

Весь процесс создания номеров сложен в классе PhonesGenerator. Для создания случайного номера (и вариаций его написания) вызовите метод generate_number:

from yaml import load, FullLoader
from phone_numbers.phone_numbers_generator import PhonesGenerator

with open('config.yaml') as f:
    config = load(f, Loader=FullLoader)

PhonesGenerator(config).generate_number()

{
'base': '8804academy', 'case_1': '8-(804)-aca-de-my', 'case_2': '8-804-aca-de-my',
'case_3': '8804-aca-de-my', 'case_4': '+8804academy', 'case_5': '8-804-academy',
'case_6': '8-804-2223369'
}

При многократном вызове метода generate_number в первую очередь отдаются номера с буквами. Слова в случайном порядке берутся из файла config.yaml, ключ seven_letter_words. Когда слова заканчиваются, то отдаются только числовые номера. Но можно и сразу генерировать числовые, для этого достаточно указать параметр generate_number (with_letters=False):

{
'base': '88062214016', 'case_1': '8-(806)-221-40-16', 'case_2': '8-806-221-40-16',
'case_3': '8806-221-40-16', 'case_4': '+88062214016', 'case_5': '8-806-2214016',
'case_6': '8-806-2214016'
}

В logs_generator.py из этого набора случайно выбирается от одного до некоторого набора вариантов. Подходящие варианты для числовых номеров задаёт константа PHONE_CASES, для буквенных — PHONE_CASES_WITH_LETTERS в файле logs_generator.py. Сами форматы определяют методы build_case_1_number, …, build_case_6_number в классе PhonesGenerator. Они же добавляются в конце метода generate_number.

Как генерируются названия спектаклей

Список спектаклей и их весов сложен в файле config.yaml. Чем выше вес, тем чаще спектакль будет в логах ticket_logs.csv. Этот процесс заложен в функции random_performance в logs_generator.py. Состав спектаклей:

• Оперы: «Севильский цирюльник», «Волшебная флейта», «Норма», «Травиата», «Евгений Онегин», «Аида», «Кармен», «Свадьба Фигаро», «Риголетто».
• Балеты: «Жизель», «Лебединое озеро», «Щелкунчик», «Спящая красавица», «Ромео и Джульетта», «Дон Кихот», «Баядерка», «Спартак».
• Мюзиклы: «Вестсайдская история», «TODD», «Юнона и Авось», «Ночь перед Рождеством», «Чикаго», «Ла-Ла Ленд», «Нотр-Дам де Пари», «Кошки».

Код класса PhonesGenerator слишком завязан на число символов в номере — это можно улучшить.

import pandas as pd

# считываем данные
qid_query = pd.read_csv("hidden_task/qid_query.tsv", sep="\t", names=["qid", "query"])
qid_url_rating = pd.read_csv("hidden_task/qid_url_rating.tsv", sep="\t", names=["qid", "url", "rating"])
hostid_url = pd.read_csv("hidden_task/hostid_url.tsv", sep="\t", names=["hostid", "url"])

# делаем join двух таблиц, чтобы было просто брать url с максимальным рейтингом
qid_url_rating_hostid = pd.merge(qid_url_rating, hostid_url, on="url")

def plook(ind, rels):
 if ind == 0:
 return 1
    return plook(ind-1, rels)*(1-rels[ind-1])*(1-0.15)

def pfound(group):
 max_by_host = group.groupby("hostid")["rating"].max() # максимальный рейтинг хоста
 top10 = max_by_host.sort_values(ascending=False)[:10] # берем топ-10 урлов с наивысшим рейтингом
 pfound = 0
    for ind, val in enumerate(top10):
 pfound += val*plook(ind, top10.values)
 return pfound

qid_pfound = qid_url_rating_hostid.groupby('qid').apply(pfound) # группируем по qid и вычисляем pfound
qid_max = qid_pfound.idxmax() # берем qid с максимальным pfound

qid_query[qid_query["qid"] == qid_max]

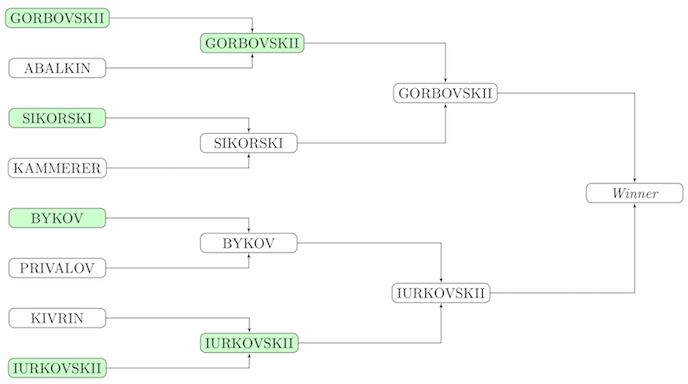
Утверждение. Набор из 2^k — 1 игр задаёт турнир по олимпийской системе тогда и только тогда,  когда:

1. В каждом псевдораунде все участники различны.
2. Количество игр в псевдораунде r равно 2^{k — r}.

Доказательство. Необходимость этих двух условий очевидна: псевдораунды соответствуют настоящим раундам турнира,  а для настоящих раундов условия верны. Достаточность докажем индукцией по k. При k = 1 есть одна игра с двумя различными участниками — это корректный олимпийский турнир. Проверим переход k — 1 → k. 

Во-первых, докажем, что каждый участник турнира играл в первом псевдораунде. Рассмотрим произвольного игрока,  пусть он участвовал в q играх. В каждом псевдораунде он мог сыграть не более одного раза,  причём в псевдораундах после q-го он не мог играть ни разу. Значит, он должен был сыграть по одному разу в каждом из псевдораундов 1, 2, …, q. Это, в частности, означает, что все люди сыграли в первом псевдораунде, а всего игроков 2^k. Теперь докажем, что в каждой из 2^{k — 1} игр первого псевдораунда был ровно один участник с n_i = 1. Как минимум один такой участник в каждой игре должен быть по определению псевдораунда. 

С другой стороны,  есть не менее 2^{k — 1} человек с n_i > 1 — это участники следующего псевдораунда. Следовательно, людей с n_i = 1 было ровно 2^{k — 1}, по одному на каждую игру. Теперь легко понять, как должен выглядеть первый раунд искомого турнира: назначим в каждой игре первого псевдораунда проигравшим участника с n_i = 1,  а победителем — участника с n_i > 1. Множество игр между победителями удовлетворяет условию для k — 1 (после выбрасывания игр из первого псевдораунда все n_i уменьшились на 1). Следовательно, этому множеству соответствует турнир по олимпийской системе.

import sys
import collections

def solve(fname):
    games = []
    for it, line in enumerate(open(fname)):
        line = line.strip()
        if not line:
            continue
        if it == 0:
            n_games = int(line)
            n_rounds = n_games.bit_length()
        else:
            games.append(line.split())

    gamer2games_cnt = collections.Counter()
    rounds = [[] for _ in range(n_rounds + 1)]

    for game in games:
        gamer_1, gamer_2 = game
        gamer2games_cnt[gamer_1] += 1
        gamer2games_cnt[gamer_2] += 1

    ok = True
    for game in games:
        gamer_1, gamer_2 = game
        game_round = min(gamer2games_cnt[gamer_1], gamer2games_cnt[gamer_2])
        if game_round > n_rounds:
            ok = False
            break
        rounds[game_round].append(game)

    finalists = list((gamer for gamer, games_cnt in gamer2games_cnt.items() if games_cnt == n_rounds))

    for cur_round in range(1, n_rounds):
        if len(rounds[cur_round]) != pow(2, n_rounds - cur_round):
            ok = False
            break
        cur_round_gamers = set()
        for gamer_1, gamer_2 in rounds[cur_round]:

            if gamer_1 in cur_round_gamers or gamer_2 in cur_round_gamers:
                ok = False
                break
            cur_round_gamers.add(gamer_1)
            cur_round_gamers.add(gamer_2)

    print ' '.join(finalists) if ok else 'NO SOLUTION'

def main():
    solve('input.txt')

if name == '__main__':
    main()