[Из песочницы] Основы компьютерной геометрии. Написание простого 3D-рендера
Привет меня зовут Давид, а вот я собственной персоной отрендеренный своим самописным рендером:
К сожалению я не смог найти более качественную бесплатную модель, но все равно выражаю благодарность заморскому скульптору запечатлевшему меня в цифре! И как вы уже догадались, речь пойдет о написании CPU — рендера.
С развитием шейдерных языков и увеличением мощностей GPU все больше людей заинтересовались программированием графики. Появились новые направления, такие как например Ray marching со стремительным ростом своей популярности.
В преддверии выхода нового монстра от NVidia я решил написать свою (ламповую и олдскульную) статью про основы рендеринга на CPU. Она является отражением моего личного опыта написания рендера, и в ней я попытаюсь довести понятия и алгоритмы с которыми я столкнулся в процессе кодинга. Стоит понимать, что производительность данного софта будет весьма низкая в силу непригодности процессора для выполнения подобных задач.
Выбор языка изначально падал на c++ или rust, но я остановился на c# из-за простоты написания кода и широких возможностей для оптимизации. Итоговым продуктом данной статьи будет рендер, способный выдавать подобные картинки:


Все модели, использованные мной здесь, распространяются в открытом доступе, не занимайтесь пиратством и уважайте труд художников!
Математика
Само собой куда же писать рендеры без понимания их математических основ. В этом разделе я изложу только те концепции, которые я использовал в коде. Тем кто не уверен в своих знаниях пропускать данный раздел не советую, без понимания этих основ трудно будет понять дальнейшее изложение. Так же я рассчитываю, что тот кто решил изучать computation geometry будет иметь базовые знания в линейной алгебре, геометрии, а так же тригонометрии (углы, вектора, матрицы, скалярное произведение). Для тех кто хочет понять вычислительную геометрию глубже, могу порекомендовать книгу Е. Никулина «Компьютерная геометрия и алгоритмы машинной графики».
Повороты вектора. Матрица поворота
Поворот — это одно из основных линейных преобразований векторного пространства. Так же оно является еще и ортогональным преобразованием, так как сохраняет длины преобразованных векторов. В двумерном пространстве существует два типа поворотов:
- Поворот относительно начала координат
- Поворот относительно некоторой точки
Здесь я рассмотрю только первый тип, т.к. второй является производным от первого и отличается лишь сменой системы координат вращения (системы координат мы разберем далее).
Давайте выведем формулы для вращения вектора в двумерном пространстве. Обозначим координаты исходного вектора — {x, y}. Координаты нового вектора, повернутого на угол f, обозначим как {x» y»}.
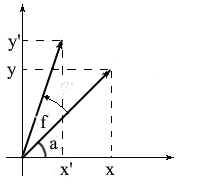
Мы знаем, что длина у этих векторов общая и поэтому можем использовать понятия косинуса и синуса для того, чтобы выразить эти вектора через длину и угол относительно оси OX:

Заметьте, что мы можем использовать формулы косинуса и синуса суммы для того, чтобы разложить значения x' и y'. Для тех, кто подзабыл я напомню эти формулы:
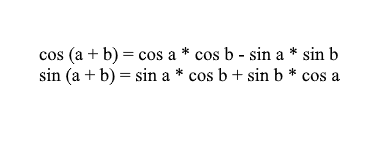
Разложив координаты повернутого вектора через них получим:

Здесь нетрудно заметить, что множители l * cos a и l * sin a — это координаты исходного вектора: x = l * cos a, y = l * sin a. Заменим их на x и y:

Таким образом мы выразили повернутый вектор через координаты исходного вектора и угол его поворота. В виде матрицы это выражение будет выглядеть так:
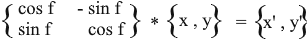
Умножьте и проверьте что результат эквивалентен тому, что мы вывели.
Поворот в трехмерном пространстве
Мы рассмотрели поворот в двумерном пространстве, а так же вывели матрицу для него. Теперь возникает вопрос, а как получить подобные преобразования для трех измерений? В двумерном случае мы вращали вектора на плоскости, здесь же бесконечное количество плоскостей относительно которых мы можем это сделать. Однако существует три базовых типа вращений, при помощи которых можно выразить любой поворот вектора в трехмерном пространстве — это XY, XZ, YZ вращения.
XY вращение.
При таком повороте мы вращаем вектор относительно оси OZ координатной системы. Представьте, что вектора — это вертолётные лопасти, а ось OZ — это мачта на которой они держаться. При XY вращении вектора будут поворачиваться относительно оси OZ, как лопасти вертолета относительно мачты.

Заметьте, что при таком вращении z координаты векторов не меняются, а меняются x и x координаты — поэтому это и называется XY вращением.
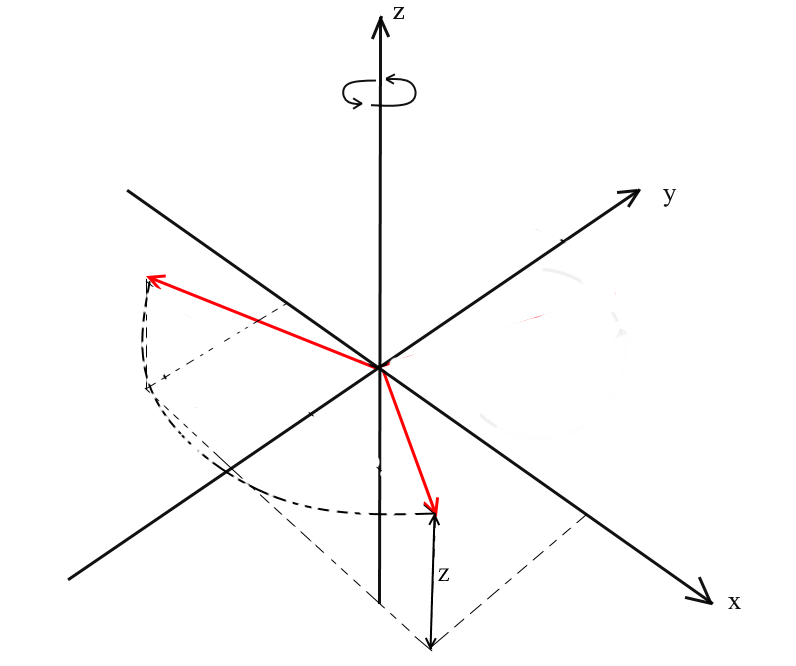
Нетрудно вывести и формулы для такого вращения: z — координата остается прежней, а x и y изменяются по тем же принципам, что и в 2д вращении.
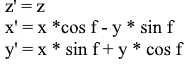
То же в виде матрицы:
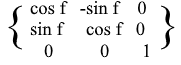
Для XZ и YZ вращений все аналогично:


Проекция
Понятие проекции может варьироваться в зависимости от контекста в котором его используют. Многие, наверное, слышали про такие понятия, как проекция на плоскость или проекция на координатную ось.
В том понимании которое мы используем здесь проекция на вектор — это тоже вектор. Его координаты — точка пересечения перпендикуляра опущенного из вектора a на b с вектором b.
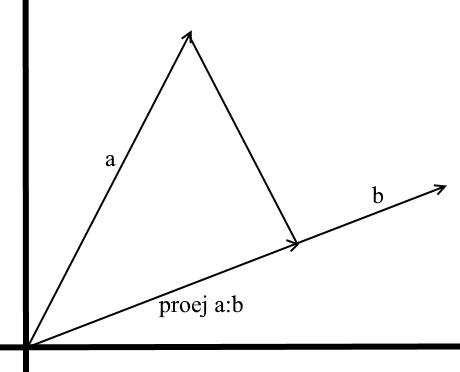
Для задания такого вектора нам нужно знать его длину и направление. Как мы знаем прилегающий катет и гипотенуза в прямоугольном треугольнике связаны отношением косинуса, поэтому используем его, чтобы выразить длину вектора проекции:
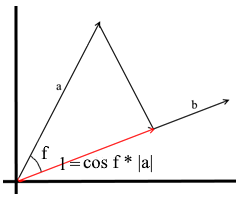
Направление вектора проекции по определению совпадает с вектором b, значит проекция определяется формулой:
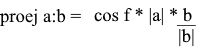
Здесь мы получаем направление проекции в виде единичного вектора и умножаем его на длину проекции. Несложно понять, что результатом будет как раз-таки то, что мы ищем.
Теперь представим все через скалярное произведение:

Получаем удобную формулу для нахождения проекции:
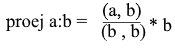
Системы координат. Базисы
Многие привыкли работать в стандартной системе координат XYZ, в ней любые 2 оси будут перпендикулярны друг другу, а координатные оси можно представить в виде единичных векторов:

На деле же систем координат бесконечное множество, каждая из них является базисом. Базис n-мерного пространства является набором векторов {v1, v2…… vn} через которые представляются все вектора этого пространства. При этом ни один вектор из базиса нельзя представить через другие его вектора. По сути каждый базис является отдельной системой координат, в которой вектора будут иметь свои, уникальные координаты.
Давайте разберем, что из себя представляет базис для двумерного пространства. Возьмём для примера всем знакомую декартову систему координат из векторов X {1, 0}, Y {0, 1}, которая является одним из базисов для двумерного пространства:
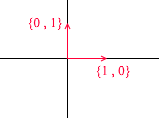
Любой вектор на плоскости можно представить в виде суммы векторов этого базиса с некими коэффициентами или же в виде линейной комбинации. Вспомните, что вы делаете когда записываете координаты вектора — вы пишете x — координату, а далее — y. Таким образом вы на самом деле определяете коэффициенты разложения по векторам базиса.

Теперь возьмём другой базис:
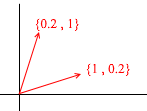
Через его вектора также можно представить любой 2д вектор:

А вот такой набор векторов не является базисом двухмерного пространства:

В нем два вектора {1,1} и {2,2} лежат на одной прямой. Какие бы их комбинации вы не брали получать будете только вектора, лежащие на общей прямой y = x. Для наших целей такие дефектные не пригодятся, однако, понимать разницу, я считаю, стоит. По определению все базисы объединяет одно свойство — ни один из векторов базиса нельзя представить в виде суммы других векторов базиса с коэффициентами или же ни один вектор базиса не является линейной комбинацией других. Вот пример набора из 3-х векторов который так же не является базисом:
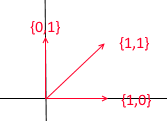
Через него можно выразить любой вектор двумерной плоскости, однако вектор {1, 1} в нем является лишним так как сам может быть выражен через вектора {1, 0} и {0,1} как {1,0} + {0,1}.
Вообще любой базис n-мерного пространства будет содержать ровно n векторов, для 2д это n соответственно равно 2.
Перейдем к 3д. Трехмерный базис будет содержать в себе 3 вектора:
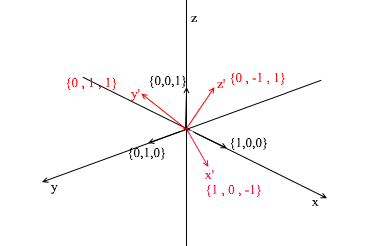
Если для двумерного базиса достаточно было двух векторов не лежащих на одной прямой, то в трехмерном пространстве набор векторов будет базисом если:
- 1)2 вектора не лежат на одной прямой
- 2)3-й не лежит на плоскости образованной двумя другими.
С данного момента базисы, с которыми мы работаем будут ортогональными (любые их вектора перпендикулярны) и нормированными (длина любого вектора базиса — 1). Другие нам просто не понадобятся. К примеру стандартный базис

удовлетворяет этим критериям.
Переход в другой базис
До сих пор мы записывали разложение вектора как сумму векторов базиса с коэффициентами:

Снова рассмотрим стандартный базис — вектор {1, 3, 6} в нем можно записать так:
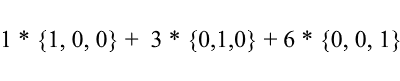
Как видите коэффициенты разложения вектора в базисе являются его координатами в этом базисе. Разберем следующий пример:
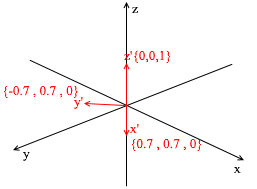
Этот базис получен из стандартного применением к нему XY вращения на 45 градусов. Возьмем вектор a в стандартной системе имеющий координаты {0,1, 1}
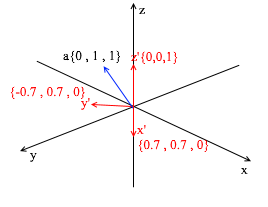
Через вектора нового базиса его можно разложить таким образом:
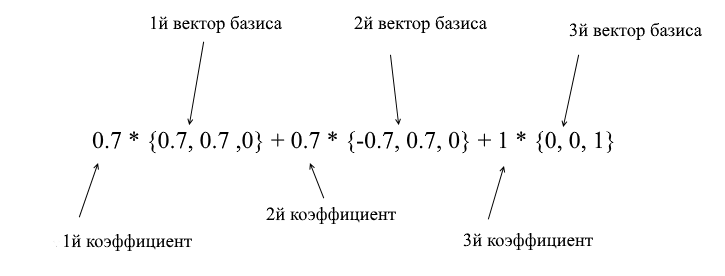
Если вы посчитаете эту сумму, то получите {0, 1, 1} — вектор а в стандартном базисе. Исходя из этого выражения в новом базисе вектор а имеет координаты {0.7, 0.7, 1} — коэффициенты разложения. Это будет виднее если взглянуть с другого ракурса:
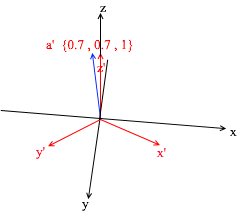
Но как находить эти коэффициенты? Вообще универсальный метод — это решение довольно сложной системы линейных уравнений. Однако как я сказал ранее использовать мы будем только ортогональные и нормированные базисы, а для них есть весьма читерский способ. Заключается он в нахождении проекций на вектора базиса. Давайте с его помощью найдем разложение вектора a в базисе X{0.7, 0.7, 0} Y{-0.7, 0.7, 0} Z{0, 0, 1}

Для начала найдем коэффициент для y». Первым шагом мы находим проекцию вектора a на вектор y» (как это делать я разбирал выше):
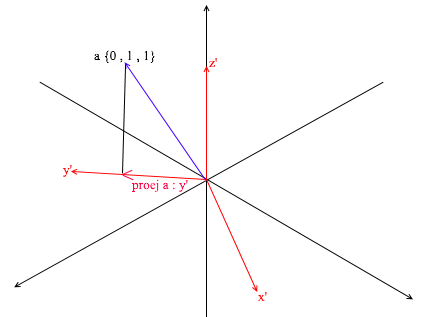
Второй шаг: делим длину найденной проекции на длину вектора y», тем самым мы узнаем «сколько векторов y» помещается в векторе проекции» — это число и будет коэффициентом для y», а также y — координатой вектора a в новом базисе! Для x» и z» повторим аналогичные операции:

Теперь мы имеем формулы для перехода из стандартного базиса в новый:
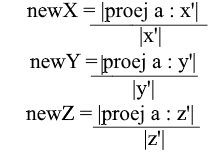
Ну, а так как мы используем только нормированные базисы и длины их векторов равны 1 отпадет необходимость делить на длину вектора в формуле перехода:
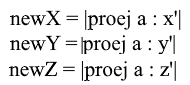
Раскроем x-координату через формулу проекции:

Заметьте, что знаменатель (x', x') и вектор x' в случае нормированного базиса так же равен 1 и их можно отбросить. Получим:

Мы видим, что координата x базисе выражается как скалярное произведение (a, x»), координата y соответственно — как (a, y»), координата z — (a, z»). Теперь можно составить матрицу перехода к новым координатам:

Системы координат со смещенным центром
У всех систем координат которые мы рассмотрели выше началом координат была точка {0,0,0}. Помимо этого существуют еще системы со смещенной точкой начала координат:
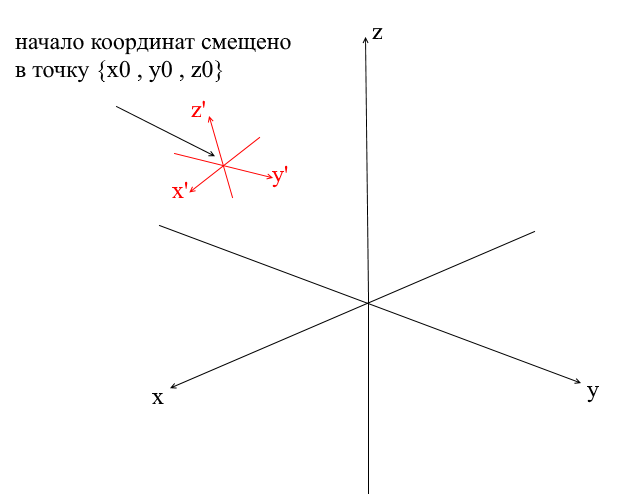
Для того, чтобы перевести вектор в такую систему нужно сначала выразить его относительно нового центра координат. Сделать это просто — вычесть из вектора этот центр. Таким образом вы как бы «передвигаете» саму систему координат к новому центу, при этом вектор остается на месте. Далее можно использовать уже знакомую нам матрицу перехода.
Пишем геометрический движок. Создание проволочного рендера.
Ну вот, думаю тому кто прошел раздел с математикой и не закрыл статью можно промывать мозги более интересными вещами! В этом разделе мы начнем писать основы 3д движка и рендеринга. Вообще рендеринг — это довольно сложная процедура, которая включает в себя много разных операций: отсечение невидимых граней, растеризация, расчет света, обработку различных эффектов, материалов (иногда даже физику). Все это мы частично разберем в дальнейшем, а сейчас мы займемся более простыми вещами — напишем проволочный рендер. Суть его в том, что он рисует объект в виде линий, соединяющих его вершины, поэтому результат выглядит похожим на сеть из проволок:

Полигональная графика
Традиционно в компьютерной графике используется полигональное представление данных трехмерных объектов. Таким образом представляются данные в форматах OBJ, 3DS, FBX и многих других. В компьютере такие данные хранятся в виде двух множеств: множество вершин и множество граней (полигонов). Каждая вершина объекта представлена своей позицией в пространстве — вектором, а каждая грань (полигон) представлена тройкой целых чисел которые являются индексами вершин данного объекта. Простейшие объекты (кубы, сферы и т.д.) состоят из таких полигонов и называются примитивами.
В нашем движке примитив будет основным объектом трехмерной геометрии — все остальные объекты будут наследоваться от него. Опишем класс примитива:
abstract class Primitive
{
public Vector3[] Vertices { get; protected set; }
public int[] Indexes { get; protected set; }
}
Пока все просто — есть вершины примитива и есть индексы для формирования полигонов. Теперь можно использовать этот класс чтобы создать куб:
public class Cube : Primitive
{
public Cube(Vector3 center, float sideLen)
{
var d = sideLen / 2;
Vertices = new Vector3[]
{
new Vector3(center.X - d , center.Y - d, center.Z - d) ,
new Vector3(center.X - d , center.Y - d, center.Z) ,
new Vector3(center.X - d , center.Y , center.Z - d) ,
new Vector3(center.X - d , center.Y , center.Z) ,
new Vector3(center.X + d , center.Y - d, center.Z - d) ,
new Vector3(center.X + d , center.Y - d, center.Z) ,
new Vector3(center.X + d , center.Y + d, center.Z - d) ,
new Vector3(center.X + d , center.Y + d, center.Z + d) ,
};
Indexes = new int[]
{
1,2,4 ,
1,3,4 ,
1,2,6 ,
1,5,6 ,
5,6,8 ,
5,7,8 ,
8,4,3 ,
8,7,3 ,
4,2,8 ,
2,8,6 ,
3,1,7 ,
1,7,5
};
}
}
int Main()
{
var cube = new Cube(new Vector3(0, 0, 0), 2);
}

Реализуем системы координат
Мало задать объект набором полигонов, для планирования и создания сложных сцен необходимо расположить объекты в разных местах, поворачивать их, уменьшать или увеличивать их в размере. Для удобства этих операций используются так называемые локальные и глобальная системы координат. Каждый объект на сцене имеет свои свою собственную систему координат — локальную, а так же собственную точку центра.
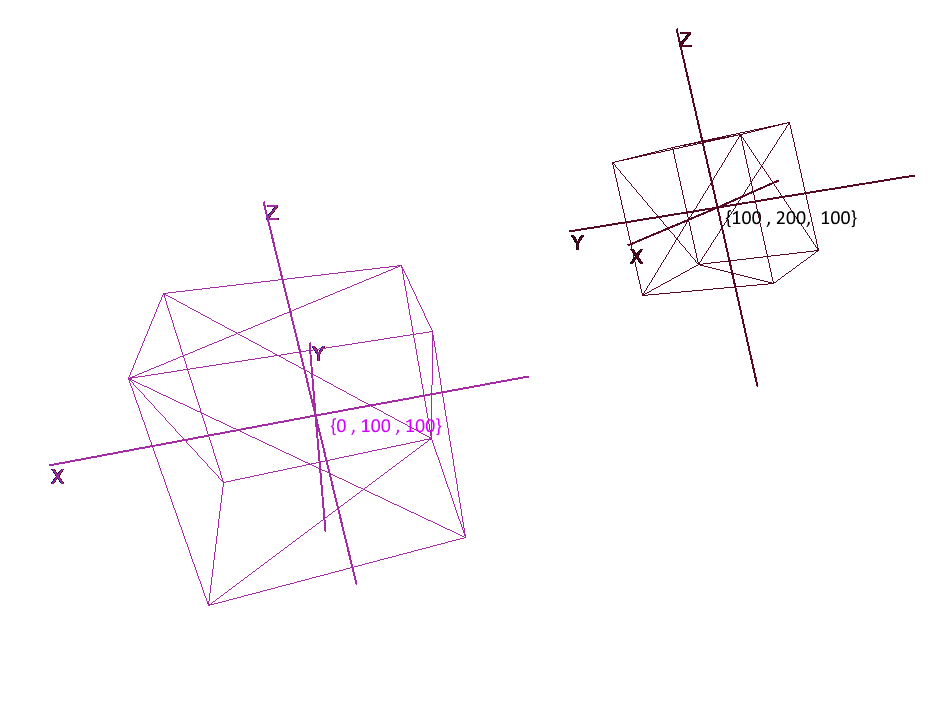
Представление объекта в локальных координатах позволяет легко производить любые операции с ним. Например, для перемещения объекта на вектор a достаточно будет сдвинуть центр его системы координат на этот вектор, для вращения объекта — повернуть его локальные координаты.
При работе с объектом мы будем производить операции с его вершинами в локальной системе координат, при рендеринге будем предварительно переводить все объекты сцены в единую систему координат — глобальную. Добавим системы координат в код. Для этого создадим объект класса Pivot (стержень, точка опоры) который будет представлять локальный базис объекта и его центральную точку. Перевод точки в систему координат представленную Pivot будет производиться в 2 шага:
- 1)Представление точки относительно центра новых координат
- 2)Разложение по векторам нового базиса
Наоборот же, чтобы представить локальную вершину объекта в глобальных координатах необходимо выполнить эти действия в обратном порядке:
- 1)Разложение по векторам глобального базиса
- 2)Представление относительно глобального центра
Напишем класс для представления систем координат:
public class Pivot
{
//точка центра
public Vector3 Center { get; private set; }
//вектора локального базиса - локальные координатные оси
public Vector3 XAxis { get; private set; }
public Vector3 YAxis { get; private set; }
public Vector3 ZAxis { get; private set; }
//Матрица перевода в локальные координаты
public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
(
XAxis.X, YAxis.X, ZAxis.X,
XAxis.Y, YAxis.Y, ZAxis.Y,
XAxis.Z, YAxis.Z, ZAxis.Z
);
//Матрица перевода в глобальные координаты
public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
(
XAxis.X , XAxis.Y , XAxis.Z,
YAxis.X , YAxis.Y , YAxis.Z,
ZAxis.X , ZAxis.Y , ZAxis.Z
);
public Vector3 ToLocalCoords(Vector3 global)
{
//Находим позицию вектора относительно точки центра и раскладываем в локальном базисе
return LocalCoordsMatrix * (global - Center);
}
public Vector3 ToGlobalCoords(Vector3 local)
{
//В точности да наоборот - раскладываем локальный вектор в глобальном базисе и находим позицию относительно глобального центра
return (GlobalCoordsMatrix * local) + Center;
}
public void Move(Vector3 v)
{
Center += v;
}
public void Rotate(float angle, Axis axis)
{
XAxis = XAxis.Rotate(angle, axis);
YAxis = YAxis.Rotate(angle, axis);
ZAxis = ZAxis.Rotate(angle, axis);
}
}
Теперь используя данный класс добавим в примитивы функции вращения, передвижения и увеличения:
public abstract class Primitive
{
//Локальный базис объекта
public Pivot Pivot { get; protected set; }
//Локальные вершины
public Vector3[] LocalVertices { get; protected set; }
//Глобальные вершины
public Vector3[] GlobalVertices { get; protected set; }
//Индексы вершин
public int[] Indexes { get; protected set; }
public void Move(Vector3 v)
{
Pivot.Move(v);
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] += v;
}
public void Rotate(float angle, Axis axis)
{
Pivot.Rotate(angle , axis);
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
}
public void Scale(float k)
{
for (int i = 0; i < LocalVertices.Length; i++)
LocalVertices[i] *= k;
for (int i = 0; i < LocalVertices.Length; i++)
GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
}
}
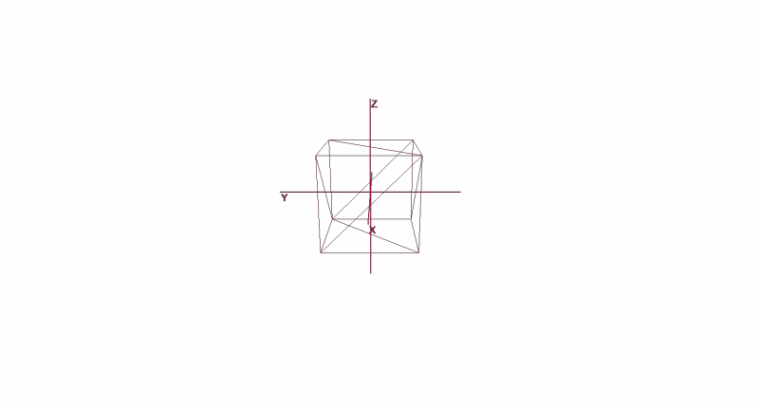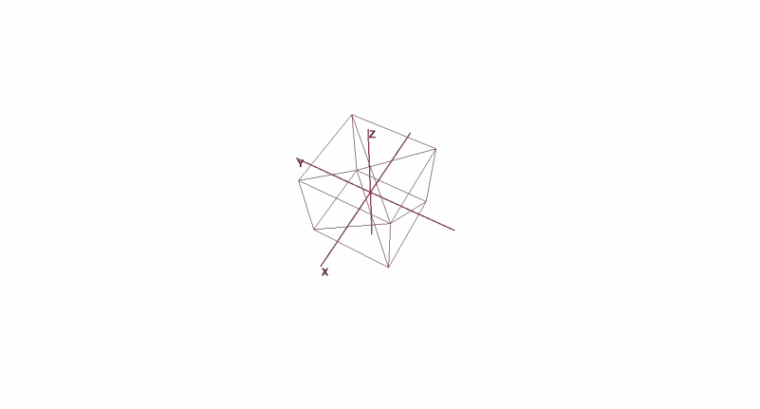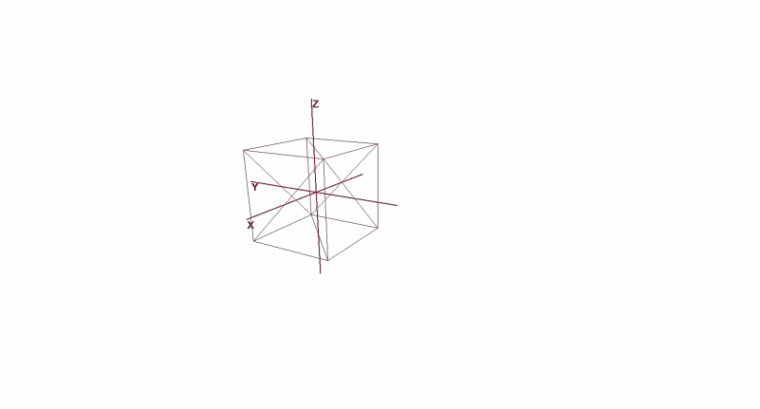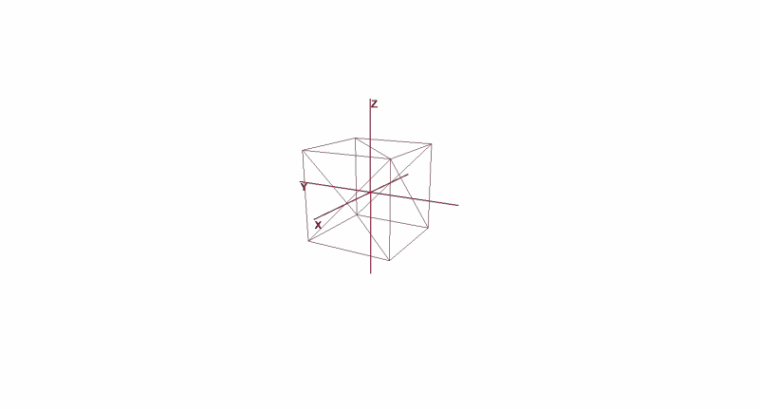
Вращение и перемещение объекта с помощью локальных координат
Рисование полигонов. Камера
Основным объектом сцены будет камера — с помощью нее объекты будут рисоваться на экране. Камера, как и все объекты сцены, будет иметь локальные координаты в виде объекта класса Pivot — через него мы будем двигать и вращать камеру:

Для отображения объекта на экране будем использовать немудреный способ перспективной проекции. Принцип на котором основан этом метод заключается в том, что чем дальше от нас расположен объект тем меньше он будет казаться. Наверное многие решали когда-то в школе задачу про измерение высоты дерева находящимся на некотором расстоянии от наблюдателя:
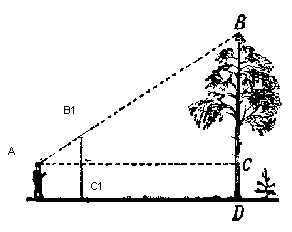
Представьте, что луч от верхней точки дерева падает на некую проекционную плоскость находящуюся на расстоянии C1 от наблюдателя и рисует на ней точку. Наблюдатель видит эту точку и хочет по ней определить высоту дерева. Как вы могли заметить высота дерева и высота точки на проекционной плоскости связанны отношением подобных треугольников. Тогда наблюдатель может определить высоту точки используя это отношение:
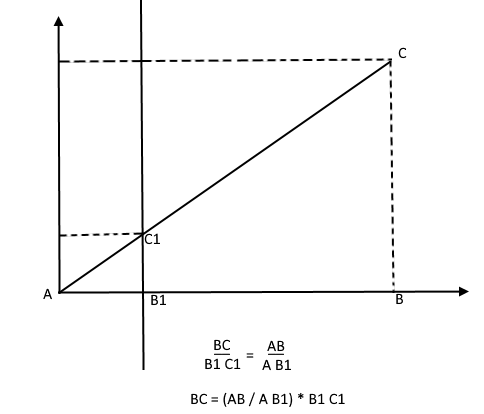
Наоборот же, зная высоту дерева он может найти высоту точки на проекционной плоскости:

Теперь вернемся к нашей камере. Представьте, что к оси z координат камеры прикреплена проекционная плоскость на расстоянии z' от начала координат. Формула такой плоскости z = z', ее можно задать одним числом — z'. На эту плоскость падают лучи от вершин различных объектов. Попадая на плоскость луч будет оставлять на ней точку. Соединяя такие точки можно нарисовать объект.

Такая плоскость будет представлять экран. Координату проекции вершины объекта на экран будем находить в 2 этапа:
- 1)Переводим вершину в локальные координаты камеры
- 2)Находим проекцию точки через отношение подобных треугольников

Проекция будет 2-мерным вектором, ее координаты x' и y' и будут определять позицию точки на экране компьютера.
public class Camera
{
//локальные координаты камеры
public Pivot Pivot { get; private set; }
//расстояние до проекционной плоскости
public float ScreenDist { get; private set; }
public Camera(Vector3 center, float screenDist)
{
Pivot = new Pivot(center);
ScreenDist = screenDist;
}
public void Move(Vector3 v)
{
Pivot.Move(v);
}
public void Rotate(float angle, Axis axis)
{
Pivot.Rotate(angle, axis);
}
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
return proection;
}
}
Данный код имеет несколько ошибок, о исправлении которых мы поговорим далее.
Отсекаем невидимые полигоны
Спроецировав таким образом на экран три точки полигона мы получим координаты треугольника который соответствует отображению полигона на экране. Но таким образом камера будет обрабатывать любые вершины, включая те, чьи проекции выходят за область экрана, если попытаться нарисовать такую вершину велика вероятность словить ошибок. Камера так же будет обрабатывать полигоны которые находятся позади нее (координаты z их точек в локальном базисе камеры меньше z') — такое «затылковое» зрение нам тоже ни к чему.
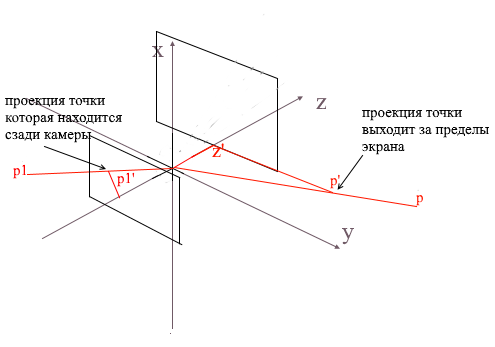
Для отсечения невидимых вершин в open gl используются метод усекающей пирамиды. Заключается он в задании двух плоскостей — ближней(near plane) и дальней(far plane). Все, что лежит между этими двумя плоскостями будет подлежать дальнейшей обработке. Я же использую упрощенный вариант с одной усекающей плоскостью — z'. Все вершины, лежащие позади нее будут невидимыми.
Добавим в камеру два новых поля — ширину и высоту экрана.
Теперь каждую спроецированную точку будем проверять на попадание в область экрана. Так же отсечем точки позади камеры. Если точка лежит сзади или ее проекция не попадает на экран то метод вернет точку {float.NaN, float.NaN}.
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
//если точка принадлежит экранной области - вернем ее
if (proection.X >= 0 && proection.X < ScreenWidth && proection.Y >= 0 && proection.Y < ScreenHeight)
{
return proection;
}
return new Vector2(float.NaN, float.NaN);
}
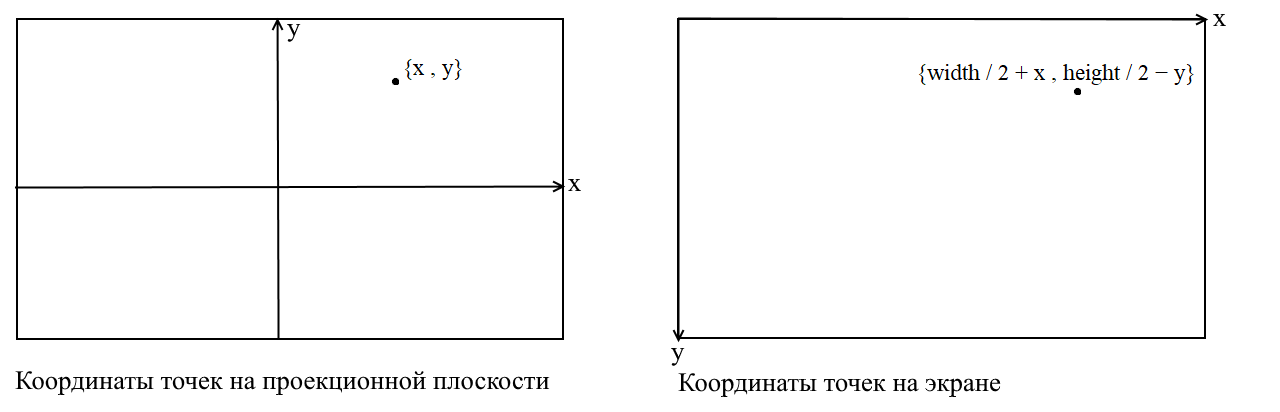
Переводим в экранные координаты
Здесь я разъясню некоторый момент. Cвязан он с тем, что во многих графических библиотеках рисование происходит в экранной системе координат, в таких координатах начало — это верхняя левая точка экрана, x увеличивается при движении вправо, а y — при движении вниз. В нашей проекционной плоскости точки представлены в обычных декартовых координатах и перед отрисовкой необходимо переводить эти координаты в экранные. Сделать это нетрудно, нужно только сместить начало координат в верхний левый угол и инвертировать y:
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию
var delta = ScreenDist / local.Z;
var proection = new Vector2(local.X, local.Y) * delta;
//этот код нужен для перевода проекции в экранные координаты
var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
var screenCoords = new Vector2(screen.X, -screen.Y);
//если точка принадлежит экранной области - вернем ее
if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
{
return screenCoords;
}
return new Vector2(float.NaN, float.NaN);
}
Корректируем размер спроецированного изображения
Если вы используете предыдущий код для того, чтобы нарисовать объект то получите что-то вроде этого:

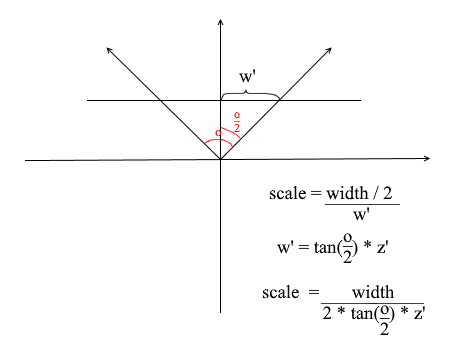
Почему — то все объекты рисуются очень маленькими. Для того, чтобы понять причину вспомните как мы вычисляли проекцию — умножали x и y координаты на дельту отношения z' / z. Это значит, что размер объекта на экране зависит от расстояния до проекционной плоскости z'. А ведь z' мы можем задать сколь угодно маленьким значением. Значит нам нужно корректировать размер проекции в зависимости от текущего значения z'. Для этого добавим в камеру еще одно поле — угол ее обзора.

Он нам нужен для сопоставления углового размера экрана с его шириной. Угол будет сопоставлен с шириной экрана таким образом: максимальный угол в пределах которого смотрит камера — это левый или правый край экрана. Тогда максимальный угол от оси z камеры составляет o / 2. Проекция, которая попала на правый край экрана должна иметь координату x = width / 2, а на левый: x = -width / 2. Зная это выведем формулу для нахождения коэффициента растяжения проекции:
public float ObserveRange { get; private set; }
public float Scale => ScreenWidth / (float)(2 * ScreenDist * Math.Tan(ObserveRange / 2));
public Vector2 ScreenProection(Vector3 v)
{
var local = Pivot.ToLocalCoords(v);
//игнорируем точки сзади камеры
if (local.Z < ScreenDist)
{
return new Vector2(float.NaN, float.NaN);
}
//через подобные треугольники находим проекцию и умножаем ее на коэффициент растяжения
var delta = ScreenDist / local.Z * Scale;
var proection = new Vector2(local.X, local.Y) * delta;
//этот код нужен для перевода проекции в экранные координаты
var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
var screenCoords = new Vector2(screen.X, -screen.Y);
//если точка принадлежит экранной области - вернем ее
if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
{
return screenCoords;
}
return new Vector2(float.NaN, float.NaN);
}
Вот такой простой код отрисовки я использовал для теста:
public DrawObject(Primitive primitive , Camera camera)
{
for (int i = 0; i < primitive.Indexes.Length; i+=3)
{
var color = randomColor();
// индексы вершин полигона
var i1 = primitive.Indexes[i];
var i2 = primitive.Indexes[i+ 1];
var i3 = primitive.Indexes[i+ 2];
// вершины полигона
var v1 = primitive.GlobalVertices[i1];
var v2 = primitive.GlobalVertices[i2];
var v3 = primitive.GlobalVertices[i3];
// рисуем полигон
DrawPolygon(v1,v2,v3 , camera , color);
}
}
public void DrawPolygon(Vector3 v1, Vector3 v2, Vector3 v3, Camera camera , color)
{
//проекции вершин
var p1 = camera.ScreenProection(v1);
var p2 = camera.ScreenProection(v2);
var p3 = camera.ScreenProection(v3);
//рисуем полигон
DrawLine(p1, p2 , color);
DrawLine(p2, p3 , color);
DrawLine(p3, p2 , color);
}
Давайте проверим рендер на сцене и кубов:
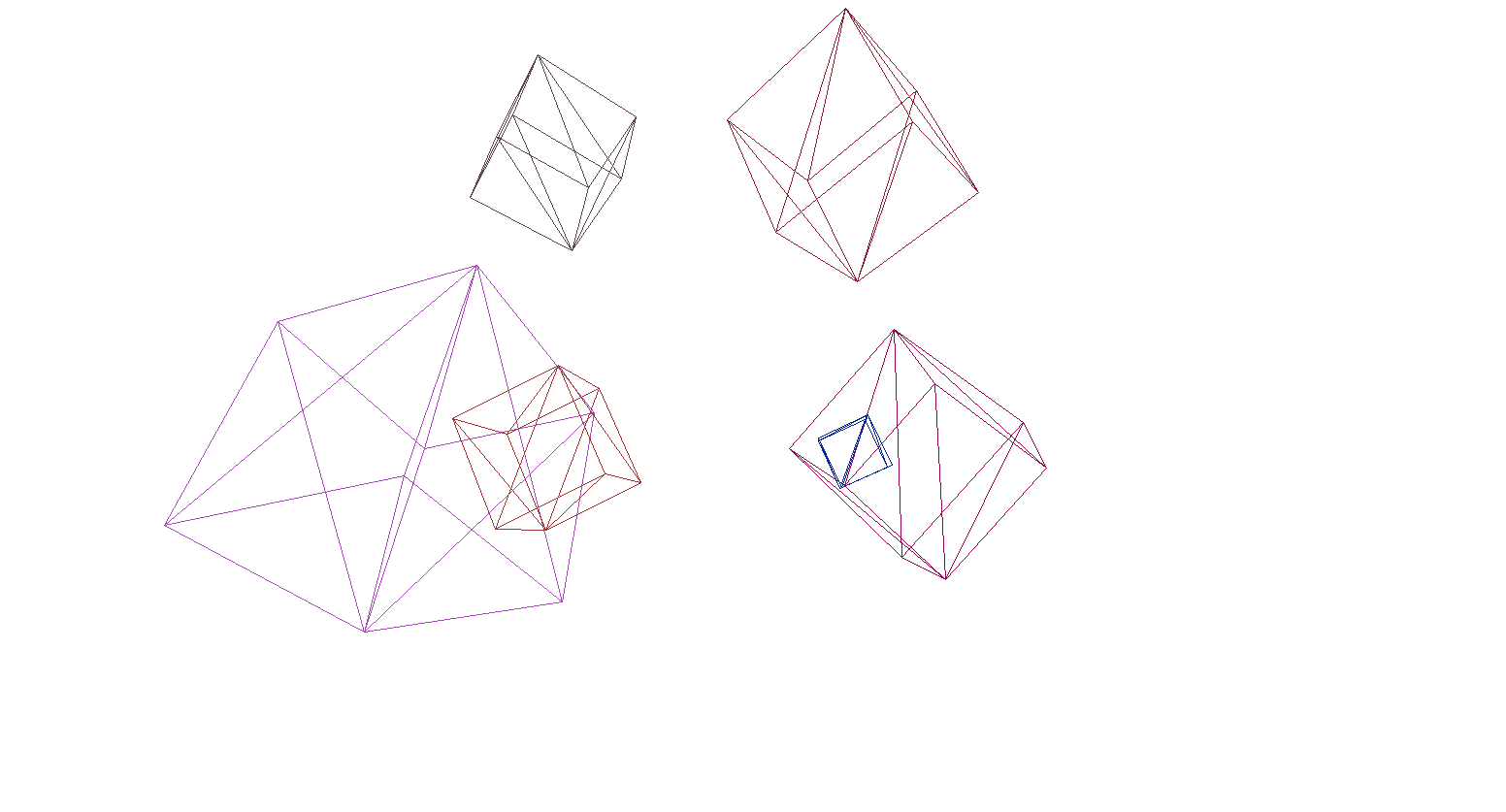
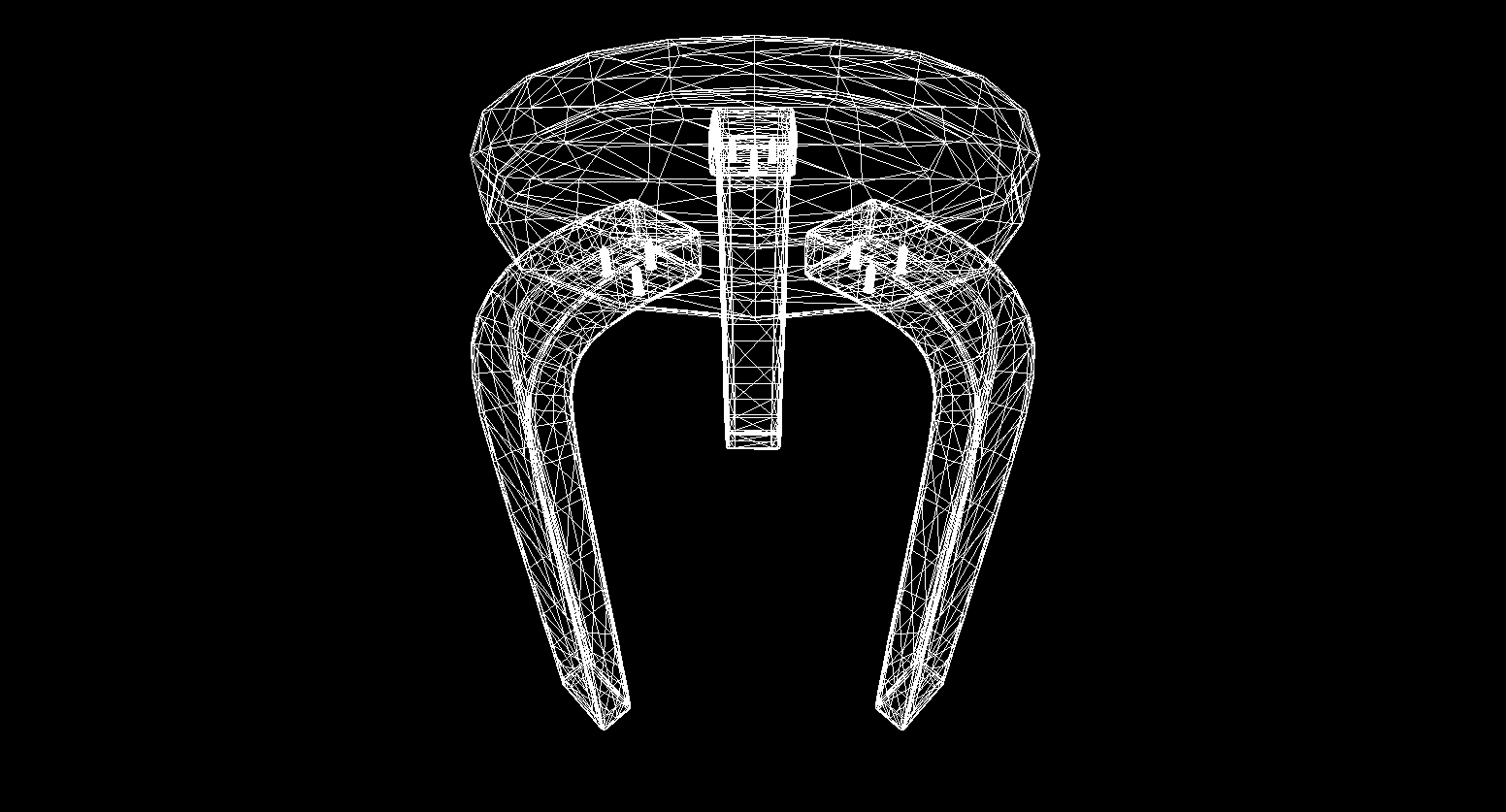
И да, все прекрасно работает. Для тех, кому разноцветные кубики не кажутся пафосными я написал функцию парсинга моделей формата OBJ в объекты типа Primitive, залил фон черным и отрисовал несколько моделей:

Растеризация полигонов. Наводим красоту.
В прошлом разделе мы написали проволочный рендер. Теперь мы займемся его модернизацией — реализуем растеризацию полигонов.
По простому растеризировать полигон — это значит закрасить его. Казалось бы зачем писать велосипед, когда есть уже готовые функции растеризации треугольника. Вот что будет если нарисовать все дефолтными инструментами:

Современное искусство, полигоны сзади нарисовались поверх передних, одним словом — каша. К тому же как таким образом текстурировать объекты? Да, никак. Значит нам нужно написать свой имба-растерайзер, который будет уметь в отсечение невидимых точек, текстуры и даже в шейдеры! Но для того чтобы это сделать стоит понять как вообще красить треугольники.
Алгоритм Брезенхема для рисования линии.
Начнем с линий. Если кто не знал алгоритм Брезенхема — это основной алгоритм рисования прямых в компьютерной графике. Он или его модификации используется буквально везде: рисование прямых, отрезков, окружностей и т.п. Кому интересно более подробное описание — читайте вики. Алгоритм Брезенхема
Имеется отрезок соединяющий точки {x1, y1} и {x2, y2}. Чтобы нарисовать отрезок между ними нужно закрасить все пиксели которые попадают на него. Для двух точек отрезка можно найти x-координаты пикселей в которых они лежат: нужно лишь взять целые части от координат x1 и x2. Чтобы закрасить пиксели на отрезке запускаем цикл от x1 до x2 и на каждой итерации вычисляем y — координату пикселя который попадает на прямую. Вот код:
void Brezenkhem(Vector2 p1 , Vector2 p2)
{
int x1 = Floor(p1.X);
int x2 = Floor(p2.X);
if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
float d = (p2.Y - p1.Y) / (x2 - x1);
float y = p1.Y;
for (int i = x1; i <= x2; i++)
{
int pixelY = Floor(y);
FillPixel(i , pixelY);
y += d;
}
}

Картинка из вики
Растеризация треугольника. Алгоритм заливки
Линии рисовать мы умеем, а вот с треугольниками будет чуть посложнее (не намного)! Задача рисования треугольника сводится к нескольким задачам рисования линий. Для начала разобьем треугольник на две части предварительно отсортировав точки в порядке возрастания x:
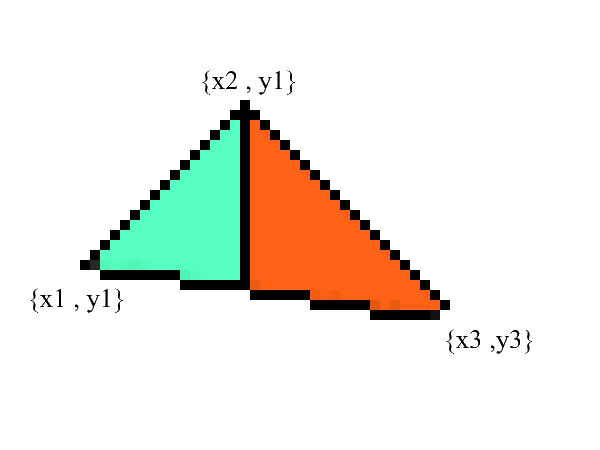
Заметьте — теперь у нас есть две части в которых явно выражены нижняя и верхняя границы. все что осталось — это залить все пиксели находящиеся между ними! Сделать это можно в 2 цикла: от x1 до x2 и от x3 до x2.
void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
//хардкодим BubbleSort для упорядочивания по x
if (v1.X > v2.X) { Swap(v1, v2); }
if (v2.X > v3.X) { Swap(v2, v3); }
if (v1.X > v2.X) { Swap(v1, v2); }
//узнаем на сколько увеличивается y границ при увеличении x
//избегаем деления на 0: если x1 == x2 значит эта часть треугольника - линия
var steps12 = max(v2.X - v1.X , 1);
var steps13 = max(v3.X - v1.X , 1);
var upDelta = (v2.Y - v1.Y) / steps12;
var downDelta = (v3.Y - v1.Y) / steps13;
//верхняя граница должна быть выше нижней
if (upDelta < downDelta) Swap(upDelta , downDelta);
//изначально у координаты границ равны y1
var up = v1.Y;
var down = v1.Y;
for (int i = (int)v1.X; i <= (int)v2.X; i++)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i , g);
}
up += upDelta;
down += downDelta;
}
//все то же самое для другой части треугольника
var steps32 = max(v2.X - v3.X , 1);
var steps31 = max(v1.X - v3.X , 1);
upDelta = (v2.Y - v3.Y) / steps32;
downDelta = (v1.Y - v3.Y) / steps31;
if (upDelta < downDelta) Swap(upDelta, downDelta);
up = v3.Y;
down = v3.Y;
for (int i = (int)v3.X; i >=(int)v2.X; i--)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i, g);
}
up += upDelta;
down += downDelta;
}
}
Несомненно этот код можно отрефакторить и не дублировать цикл:
void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
if (v1.X > v2.X) { Swap(v1, v2); }
if (v2.X > v3.X) { Swap(v2, v3); }
if (v1.X > v2.X) { Swap(v1, v2); }
var steps12 = max(v2.X - v1.X , 1);
var steps13 = max(v3.X - v1.X , 1);
var steps32 = max(v2.X - v3.X , 1);
var steps31 = max(v1.X - v3.X , 1);
var upDelta = (v2.Y - v1.Y) / steps12;
var downDelta = (v3.Y - v1.Y) / steps13;
if (upDelta < downDelta) Swap(upDelta , downDelta);
TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);
upDelta = (v2.Y - v3.Y) / steps32;
downDelta = (v1.Y - v3.Y) / steps31;
if (upDelta < downDelta) Swap(upDelta, downDelta);
TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}
void TrianglePart(float x1 , float x2 , float y1 , float upDelta , float downDelta)
{
float up = y1, down = y1;
for (int i = (int)x1; i <= (int)x2; i++)
{
for (int g = (int)down; g <= (int)up; g++)
{
FillPixel(i , g);
}
up += upDelta; down += downDelta;
}
}
Отсечение невидимых точек.
Для начала подумайте каким образом вы видите. Сейчас перед вами экран, а то что находится позади него скрыто от ваших глаз. В рендеринге работает примерно такой же механизм — если один полигон перекрывает другой рендер нарисует его поверх перекрытого. Наоб
