Формула Байеса и где ее использовать03.01.2023 03:02

Результат формулы Байеса показывает, как поступление новых данных о событии влияет на вероятность исхода этого события. Применений данной формулы крайне много, вот несколько примеров:

Мы же разберемся в самой формуле. Для этого попробуем ответить на два вопроса:

Давайте начнем с того, что рассмотрим 100 человек, 10 мужчин и 90 женщин. Тогда вероятность случайно встретить мужчину 10%, а женщину 90%. Далее нам известно, что среди 10 мужчин 4 имеют светлые волосы, а среди 90 женщин только 9. Тогда вероятность встретить мужчину с светлыми волосами будет 4/10=0.4 (40%), а женщину 9/90=0.1 (10%).

Зададимся простым вопросом: Если мы встретили человека со светлыми волосами, то с какой вероятностью он будет мужчиной? Логично, что искомая вероятность рассчитывается по формуле: 4/(9+4) = 0.307 (30.7%), так как всего 13 возможных вариантов встретить человека со светлыми волосами и всего 4 удовлетворяют условию. Давайте распишем эту формулу через имеющиеся вероятности и общее число людей:

$30,7 = \frac{100*0.1*0.4}{100*0.9*0.1+100*0.1*0.4}$

как видно от общего числа людей итоговая вероятность не зависит. Тогда можно более формально записать получившуюся формулу и получить формулу Байеса:

$\small P(H|E)= \frac{P(H)*P(E|H)}{P(E)} = \frac{P(H)*P(E|H)}{P(\overline{H})*P(E|\overline{H})+P(H)*P(E|H)}$

Где H — это гипотеза о том, что встретили мужчину; P (H) — вероятность встретить мужчину (Априорная вероятность); P (E|H) — вероятность встретить человека со светлыми волосами, при условии, что встретили мужчину (правдоподобие). H^- вероятность встретить женщину. P (H|E) — вероятность того, что случайно встретившийся человек со светлыми волосами — мужчина (апостериорная вероятность). P (E) — полная вероятность наступления события E.

Наглядно это можно показать с помощью областей, а точнее их площадей:

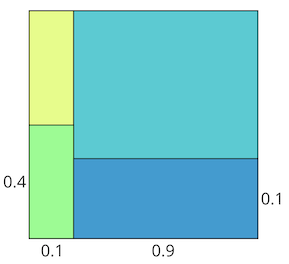
По горизонтали у нас определена априорная вероятность для H и H^, а по вертикали вероятности правдоподобия. Тогда площади нижних прямоугольников будут соответствовать следующим вероятностям:

$P(H)*P(E|H) \ и\ P(\overline{H})*P(E|\overline{H})$

Но стоит понимать, что такая визуализация помогает далеко не во всех случаях. Далее мы рассмотрим пару примеров, когда апостериорная вероятность находится более сложным путем (или нет :)).

Напишем небольшой код, чтобы визуально продемонстрировать смысл формулы Байеса

from ipywidgets import interact
def bayes(H,E_H, E_not_H):
    
    plt.axes()
    rectangle = plt.Rectangle((0,0), 1, 1, fc='paleturquoise',ec="w")
    rectangle2 = plt.Rectangle((0,0), H, E_H, fc='mediumseagreen',ec="w")
    rectangle3 = plt.Rectangle((H,0), 1-H, E_not_H, fc='mediumaquamarine',ec="w")
    plt.gca().add_patch(rectangle)
    plt.gca().add_patch(rectangle2)
    plt.gca().add_patch(rectangle3)
    plt.axis('scaled')
    
    plt.show()
    return 'Вероятность, что гипотеза H верна с учетом новвых данных P(H|E):',round( 
            ( H*E_H )/(
                H*E_H + (1-H)*E_not_H ), 2)
#interact данная функция позволит оживить наш график 
#и задавать параметры функции через ползунок
interact(bayes, H = (0.0,1.0,0.01), E_H = (0.0,1.0,0.01), E_not_H = (0.0,1.0,0.01) )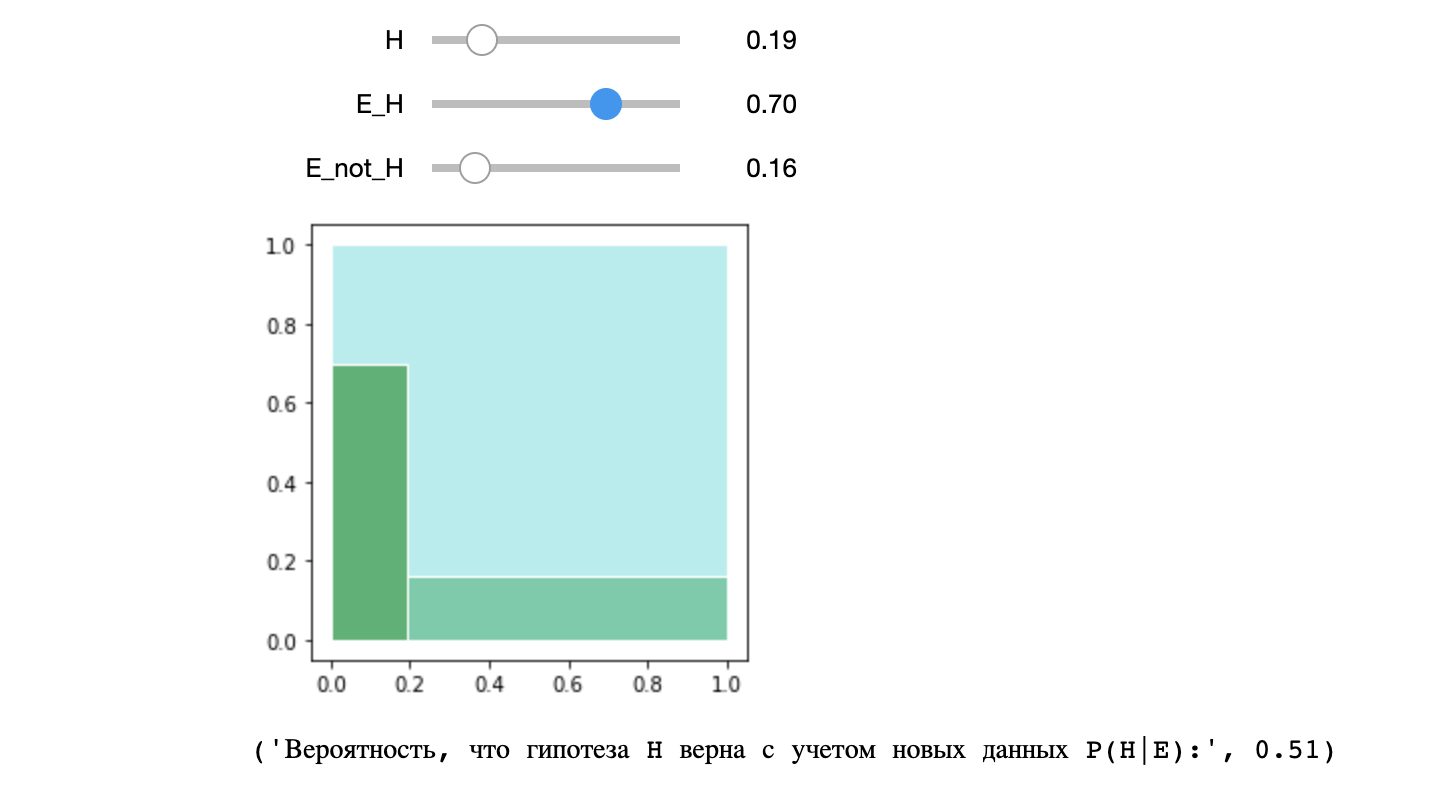

Рассмотрим квадратный стол. Мы знаем, что задана некоторая точка на этом столе, местоположение которой нам неизвестно. Далее бросают шарик и говорят нам, как упал шарик относительно зафиксированной точки — левее или правее (выше или ниже). Нам необходимо на имеющихся данных определить область, в которой зафиксирована точка.

Эту задачу можно перенести на координатную плоскость [0,1]х[0,1]. И каждую сторону поделив на 4 части, получим 16 областей, в одной из которых зафиксирована наша точка:

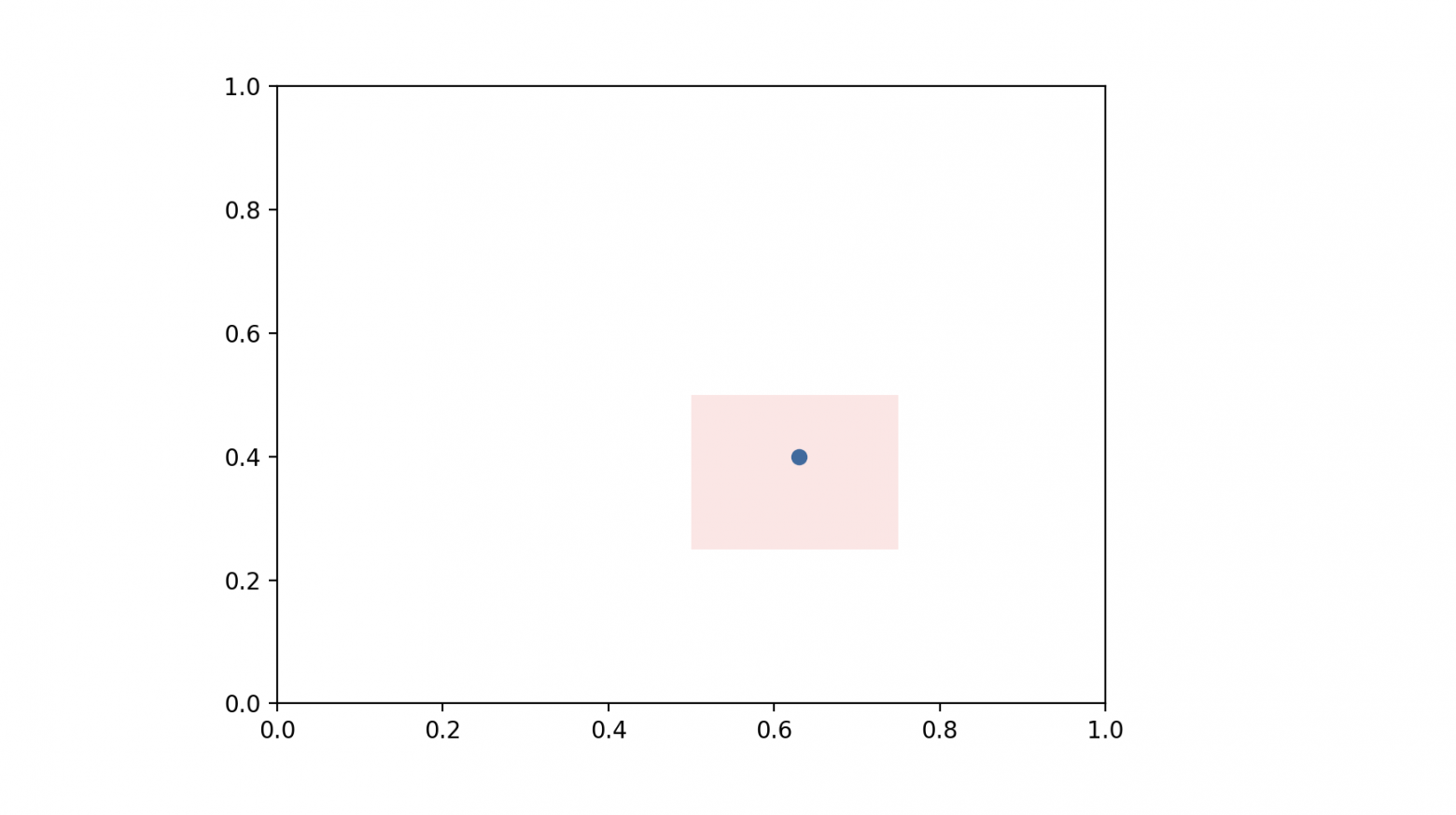
Именно эту область нам и нужно определить с помощью формулы Байеса. Давайте для этого рассмотрим сначала одномерный случай, то есть рассмотрим отрезок от 0 до 1 и условимся, что на нем зафиксирована точка и у нас есть 4 отрезка, в которых эта точка может лежать : [0,0.25], [0.25,0.5], [0.5,0.75], [0.75,1]. Вопрос, а почему не полуинтервалы, упустим. Пусть наша зафиксированная точка равняется 0.4.

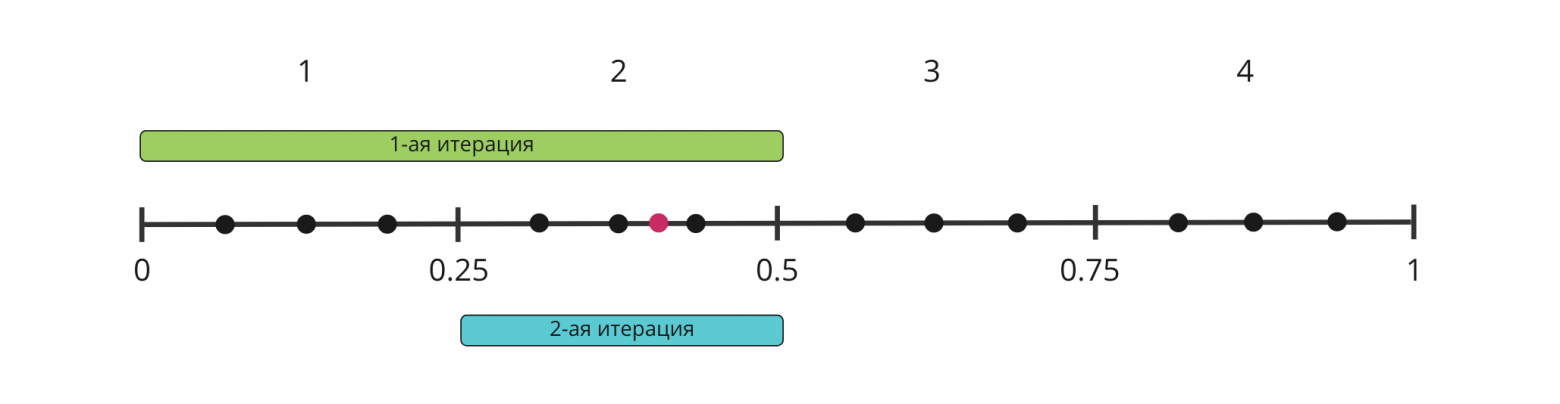
Тогда наша первая итерация будет заключаться в проверке гипотезы H: Точка X лежит в [0, 0.5]. И H^: Точка X лежит в [0.5, 1]. Так как это первый шаг, то точка может лежать равновероятно и по правую, и по левую сторону от 0.5.

Произведем первый шаг. E: Точка выпала правее X — это наше условие, новое знание, которое мы получили в ходе эксперимента.

На рисунке выше мы разбили наш отрезок на N=16 подобластей. Если гипотеза верна, то точка может занять любую из N/2=8 подобластей. Тогда для выполнения E будут удовлетворять от N/2=8 до N-1=15 подобластей. Из этого можно посчитать число удовлетворяющих нас исходов, оно будет определяться из суммы алгебраической прогрессии:

$\small S(n) = \frac{a_1+a_n}{2} *n = \frac{\frac{N}{2}+N-1}{2} *\frac{N}{2} = \frac{3N^2}{8} - \frac{N}{4} = \frac{8+15}{2} *8$

При выполнении H всего исходов у нас N/2 * N (Здесь мы говорим только про выполнение H, E здесь не учитывается). Тогда вероятность, что при верности гипотезы точка выпадет правее X будет следующей:

$\small P(E|H) = \frac{S(n)}{ \frac{N^2}{2}} = \frac{3}{4} - \frac{1}{2N}$

Если начнем увеличивать число разбиений, то эта вероятность все больше будет стремиться к 0.75, поэтому ее и будем использовать.

Аналогичным образом можем определить вероятность P (E'|H), где E': Точка выпала левее X — это наше условие, новое знание, которое мы получили в ходе эксперимента. Она составит 0.25. Теперь можно записать формулу Байеса:

$\small E:\ P(H|E) = \frac{P(H)*P(E|H)}{P(\overline{H})*P(E|\overline{H})+P(H)*P(E|H)} = \frac{0.5*0.75}{0.5*0.75+0.5*0.25} = 0.75$ $\small E':\ P(H|E') = \frac{P(H)*P(E'|H)}{P(\overline{H})*P(E'|\overline{H})+P(H)*P(E'|H)} = \frac{0.5*0.25}{0.5*0.75+0.5*0.25} = 0.25$

После первого шага наши априорные вероятности изменились, так как появилось условие E (E'). Тогда для второго шага, когда у нас появится новое условие E, мы пересчитанные априорные вероятности подставим в формулу Байеса, и они снова поменяются. Таким образом, можем проделывать такие действия определенное число раз и тем самым из условия максимума итоговых априорных вероятностей выбрать, по какую сторону от точки 0.5 лежит X. Вопрос о выборе кол-ва шагов в первой итерации остается открытым и предлагаем вам самим ответить на него.

Пусть из наших k экспериментов мы определили, что X лежит слева от 0.5. Теперь давайте сделаем 2-ую итерацию и определим, в каком отрезке она лежит, в 1-ом или во 2-ом. Для этого введем новую гипотезу:
H: Точка X лежит во 2-ом отрезке.

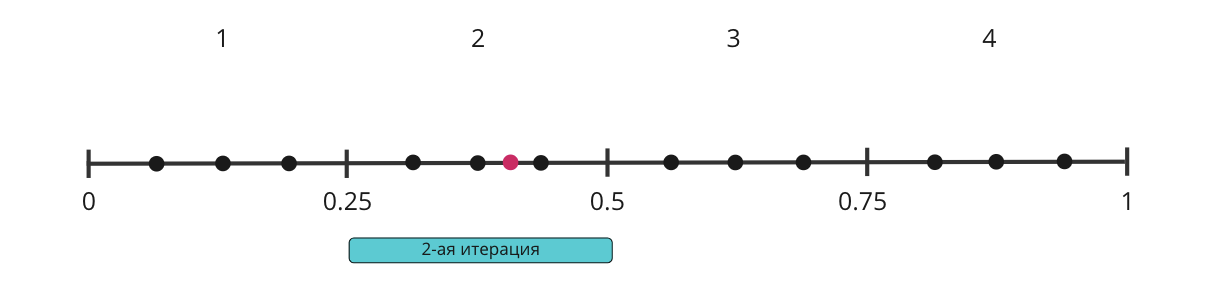
В силу 1-ой итерации и новой гипотезы точка либо лежит в 1-ом отрезке, либо во 2-ом, причем равновероятно.

Произведем первый шаг. E: Точка выпала правее X — это наше условие, новое знание, которое мы получили в ходе эксперимента.

По аналогии смотрим все исходы и те, что удовлетворяют E:

$\small S(n) = \frac{a_1+a_n}{2} *n = \frac{\frac{N}{2}+\frac{3N}{4}-1}{2} *\frac{N}{4} = \frac{5N^2}{32} - \frac{N}{8}$

А всего исходов у нас N/4 * N. Тогда вероятность, что при верности гипотезы точка выпадет правее X, будет следующей:

$P(E|H) = \frac{S(n)}{ \frac{N^2}{4}} = \frac{\frac{5N^2}{32} - \frac{N}{8} }{ \frac{N^2}{4}} = \frac{5}{8} - \frac{1}{2N}$

При увеличении N дает нам 0.625.

Теперь для обратного условия E':

$\small S(n) = \frac{a_1+a_n}{2} *n = \frac{\frac{N}{4}+\frac{N}{2}-1}{2} *\frac{N}{4} = \frac{3N^2}{32} - \frac{N}{8}$ $\small P(E'|H) = \frac{S(n)}{ \frac{N^2}{4}} = \frac{\frac{3N^2}{32} - \frac{N}{8} }{ \frac{N^2}{4}} = \frac{3}{8} - \frac{1}{2N}$

Получаем 0.375 при увеличении N.

В формуле Байеса присутствует альтернативная гипотеза H^, в нашем случае это гипотеза, что X лежит в 1-ом отрезке. Аналогичными действиями можно найти следующие вероятности:

$\small P(E|\overline{H}) = 0.875$ $\small P(E'|\overline{H}) = 0.125$

Нам осталось записать 4 формулы Байеса, которые покроют два исхода E и E', и вычислят новые значения для априорных вероятностей

$\small E:\ P(H|E) = \frac{P(H)*P(E|H)}{P(\overline{H})*P(E|\overline{H})+P(H)*P(E|H)} = \frac{0.5*0.625}{0.5*0.625+0.5*0.875}$ $\small E:\ P(\overline{H}|E) = \frac{P(H)*P(E|H)}{P(\overline{H})*P(E|\overline{H})+P(H)*P(E|H)} = \frac{0.5*0.875}{0.5*0.625+0.5*0.875}$ $\small E':\ P(H|E') = \frac{P(H)*P(E'|H)}{P(\overline{H})*P(E'|\overline{H})+P(H)*P(E'|H)} = \frac{0.5*0.375}{0.5*0.375+0.5*0.125}$ $\small E':\ P(\overline{H}|E') = \frac{P(H)*P(E'|H)}{P(\overline{H})*P(E'|\overline{H})+P(H)*P(E'|H)} = \frac{0.5*0.125}{0.5*0.375+0.5*0.125}$

Для случая, когда X лежит по правую сторону от 0.5, результат будет зеркальным относительно того, что мы сейчас получили.

По аналогии с 1-ой итерацией мы можем проделать n шагов и выбрать тот отрезок, в котором наиболее вероятно находится точка Х.

Напишем простую для восприятия функцию в Python, которая будет проделывать описанные выше шаги:

def Bayes(Target_x):
    P_H_E__left = 1
    P_H_E__right = 1
    area = 'left'
    x0=0
    x1=1
    left_step1 = 0
    right_step1 = 0
    left_step2 = 0
    right_step2 = 0
    for j in range(1,3):
        P_H_E__left = 1
        P_H_E__right = 1
        P_H_E_internal = 1
        P_H_E__external = 1
        for I in range(1000):
            next_point_x = round(random.random(),2)
            if j==1:
                #Для перовй итерации запишем формулу Байеса для E (else) и E' (if)
                if next_point_xTarget_x:
                    P_H_E_internal = P_H_E_internal*0.375/ (P_H_E_internal*0.375 + P_H_E__external*0.125)
                    P_H_E__external = P_H_E__external*0.125/ (P_H_E_internal*0.375 + P_H_E__external*0.125)
                else:
                    P_H_E_internal = P_H_E_internal*0.625/ (P_H_E_internal*0.625 + P_H_E__external*0.875)
                    P_H_E__external = P_H_E__external*0.875/ (P_H_E_internal*0.625 + P_H_E__external*0.875)
                last_left,last_right = P_H_E_internal,P_H_E__external
        #Для каждой итерации мы должны определить итоговую область и скорректировать 
        #ее граинцы
        if j==1:
            print('1ая + 2ая области:', last_left)
            print('3яя + 4ая области:', last_right)
            if right_step1>left_step1:
                area = 'left'
                x1 = x1-(x1-x0)/2
            else:
                area='right'
                x0 = x0+(x1-x0)/2
            print(Target_x,area,x0,x1)
        if j==2:
            print('внутренняя область:', P_H_E_internal)
            print('внешняя область:', P_H_E__external)
            if P_H_E_internal>P_H_E__external: ##внутренняя четвертинка
                if area == 'left':
                    x0 = x0+(x1-x0)/2
                else:
                    x1 = x1-(x1-x0)/2
            else:
                if area == 'left':
                    x1 = x1-(x1-x0)/2
                else:
                    x0 = x0+(x1-x0)/2
    return x0,x1

Bayes(0.35)

Пример 2

Давайте рассмотрим классическую задачу с монеткой, а именно проверкой ее на честность. Данная задача хороша тем, что ее решение отлично ложится на многие реальные задачи, в которых имеется биномиальное распределение. Для того, чтобы лучше понять все происходящее с монеткой, мы пойдем от сложного к простому.

Имеется монетка и мы хотим определить, насколько она честная. То есть хотим понять: орел выпадает так же часто, как и решка, или нет.

Введем гипотезу H: Монетка симметрична, вероятность выпадения орла 0.5. Обозначим эту вероятность за p (p=0.5) вероятность успеха (выпал орел). В данной задаче p является случайной величиной, причем непрерывной.

При этом данной гипотезой мы не определили априорную вероятность. То есть гипотеза говорит нам, о свойстве монетки, что она симметрична, но не дает понимание, насколько это вероятно. Давайте запишем это неизвестное значение, а позже вернемся к нему:
P (H) — вероятность того, что монетка симметрична, и выпадение орла и решки равновероятно. P (H) — это наша априорная вероятность.

Давайте проведем эксперимент и подбросим нашу монетку 500 раз. В результате орел выпал 230 раз, а решка 270. Тем самым получили наше E — результат эксперимента. Теперь возникает вопрос:

Честная ли наша монетка? Можно перефразировать вопрос таким образом: Если мы построим 95% доверительный интервал для всех p, то значение 0.5 попадет в него или нет?

Чтобы ответить на вопрос, мы должны построить апостериорное распределение, а для этого нужно понимать, какая плотность распределения для выпадения орла у нашей монетки в априори. К плотности мы перешли в виду того, что случайная величина является непрерывной, а значит говорить про вероятность для конкретного значения нельзя, поскольку она равняется нулю. То есть нам нужно использовать формулу Байеса для каждого p из отрезка от 0 до 1, поскольку H^ вместе с H включают в себя абсолютно все исходы. И тогда сможем посчитать P (E) и это будет знаменателем формулы Байеса. А само P (E) есть полная вероятность наступления события E.

Давайте определим, как будет выглядеть формула Байеса. Мы имеем биномиальное распределение: у монетки есть только два исхода. Тогда P (E|H) можно вычислить следующим образом:

$С^{230}_{500}0.5^{230}*(1-0.5)^{500-230}$

Зная P (H), числитель для формулы Байеса у нас готов. Остается разобраться с тем, что будет в знаменателе. В знаменателе у нас есть альтернативная гипотеза H^, в нашем примере эту гипотезу можно описать так: Монетка не симметрична, вероятность выпадения орла не равняется 0.5.

Мы имеем дело с непрерывной случайно величиной, так как p у нас может быть абсолютно любым значением от 0 до 1. И решением в данной ситуации будет интегрирование от 0 до 1 выражение:

$С^{k}_n \int\limits_{0}^{1} \rho(x)x^k(1-x)^{n-k}dx$ $где\ \rho(x) - плотность\ распределения\ случайной\ величины\ p,\ k=230 \ и \ n=500$

0.5 включили в область интегрирования, так как в общем виде знаменатель имеет такой вид:

$P(\overline{H})*P(E|\overline{H})+P(H)*P(E|H)$

Итоговый вид формулы Байеса для данного примера будет таким:

$P(H|E) = \frac{С^{k}_n\rho(0.5)0.5^k(1-0.5)^{n-k} }{С^{k}_n \int\limits_{0}^{1} \rho(x)x^k(1-x)^{n-k}dx} = \frac{\rho(0.5)0.5^k(1-0.5)^{n-k} }{ \int\limits_{0}^{1} \rho(x)x^k(1-x)^{n-k}dx}$

Теперь давайте вернемся к априорной вероятности и гипотезе H.

H: p=0.5 — предполагаем, что вероятность выпадения орла для нашей монетки равна 0.5.

Тогда априорная вероятность выражает вероятность того, насколько это утверждение верно до проведения самого эксперимента.

Для определения априори есть два подхода:

Частный подход — до начала эксперимента все возможные исходы равновероятны.
Байесовский подход — задается некая априори исходя из наших знаний о событии до начала эксперимента

Для Байесовского подхода необходимо выбрать некоторое априорное распределение таким образом, чтобы наше апостериорное распределение имело тот же вид, что и априорное, только с другими параметрами. Только что мы определили термин «Сопряженное априорное распределение». Чтобы определить его для конкретной задачи, можно воспользоваться ссылкой. В нашем случае это Бета-распределение.

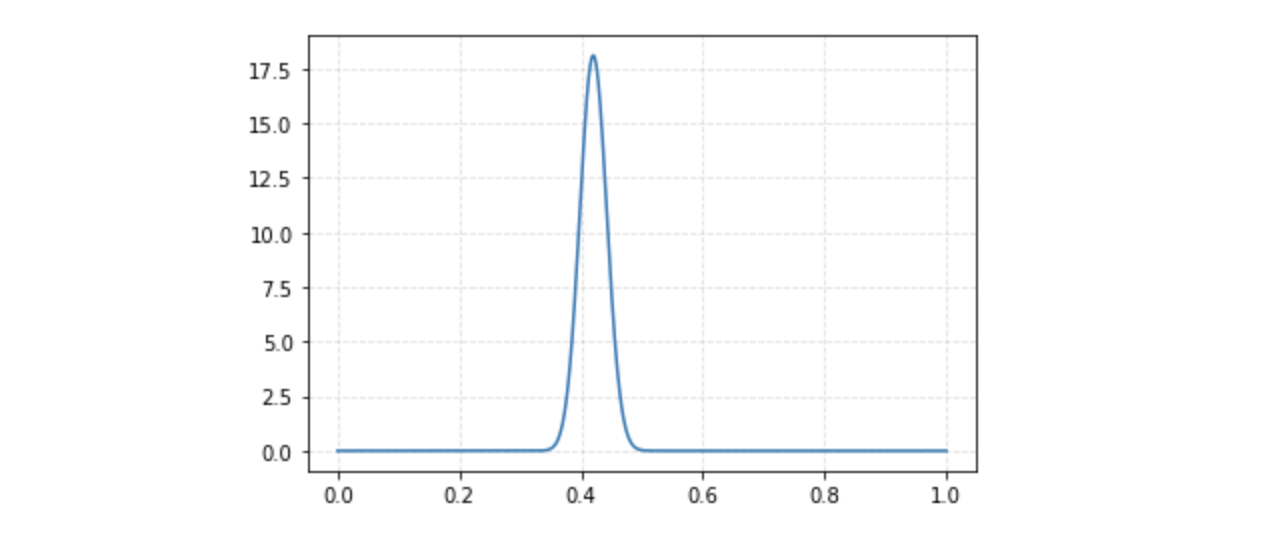
Мы пойдем по частному подходу и для бета-распределения возьмем альфа и бета равными 1. Тогда после эксперимента плотность вероятности будет выглядеть так (на выходе получили то же бета-распределение, только с параметрами альфа и бета равными 231 и 271 соответственно):

Максимум плотности вероятности будет находиться в точке ~0.46. Если построим 95% доверительный интервал, то получим [0.415, 0.506]. Получается, мы не можем отклонить гипотезу H, так как значение p=0.5 входит в 95% интервал.

Проведем еще пару мысленных экспериментов:

Из 500 бросков орел выпал 250 раз
Из 500 бросков орел выпал 210 раз

Для первого имеем доверительный интервал [0.455, 0.545], а для второго [0.376, 0.464]. Для второго случая мы уже можем сказать, что с монеткой что-то неладное, так как 0.5 в него уже не входит. А для нашего случая и 1-го эксперимента 0.5 входит в доверительный интервал и у нас нет оснований полагать, что монетка нас обманывает.

Плотности распределения для 1 и 2 эксперимента:

По факту мы не сделали ничего сверхъестественного, поскольку мы просто переопределили параметры альфа и бета для бета-распределения, поскольку выше мы ввели понятие сопряженного априорного распределения, которое должно принадлежать тому же семейству, что и апостериорное. То есть грубо говоря на выходе мы получаем то же бета-распределение, только с другими параметрами. А для вычисления этих параметров нам достаточно только результатов эксперимента и нет необходимости в вычислении сложных формул, которые расписывали выше.