Физики решили загадку уравнения «песчаных замков» 150-летней давности
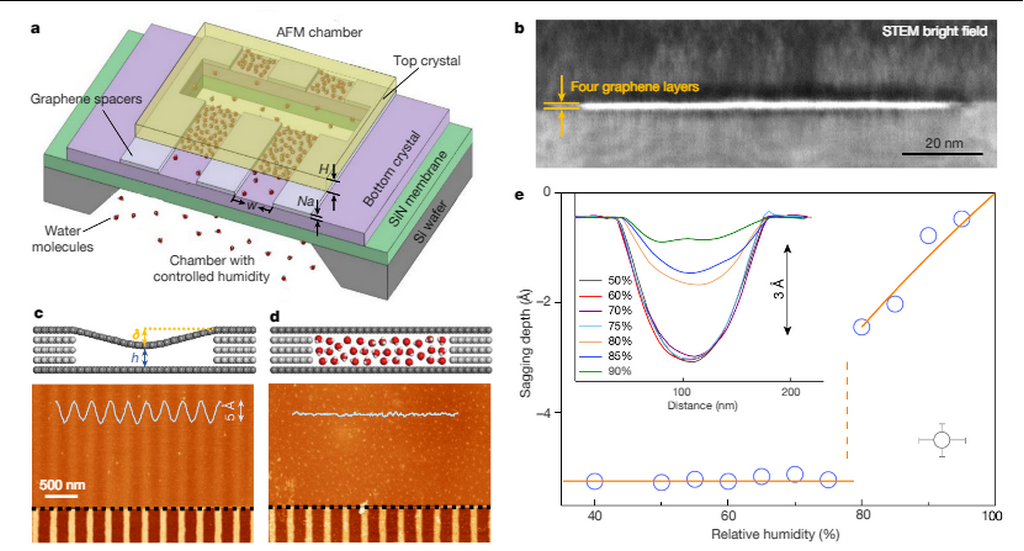Капилляры атомарного масштаба и конденсат воды внутри. а) Схема исследуемых капиллярных устройств. б) Изображение поперечного сечения четырехслойного графитового капилляра с помощью сканирующей электронной микроскопии. в и г) AFM-изображение того же капилляра слюды при относительной влажности 30% и 95% соответственно (толщина верхнего слоя = 100 нм).
Лаборатория лауреата Нобелевской премии Андре Гейма в Манчестерском университете в Англии работала над решением математической головоломки — «уравнения Кельвина», которому 150 лет. Наконец это решение было найдено.
Для строительства замка из песка нужны песок и вода; вода действует как клей, удерживающий песчинки вместе. Исследования показали, что идеальное соотношение для строительства прочного песчаного замка — это одно ведро воды на каждые восемь ведер с песком.
Еще в 2008 году физики решили немного глубже разобраться, почему песок становится липким при намокании. С помощью рентгеновской микротомографии они получили трехмерные изображения мокрых стеклянных шариков, по форме и размеру похожих на песчинки. Когда они добавляли жидкость к сухим шарикам, то наблюдали образование жидких «капиллярных мостиков» между ними. Добавление большего количества жидкости привело к тому, что мостики стали больше, и это еще больше увеличило связывающий эффект. Однако усиление связывающего эффекта нивелировалось соответствующим уменьшением капиллярных сил по мере роста мостиковых структур.
Команда пришла к выводу, что, даже если содержание влаги изменится, силы, связывающие шарики, не изменятся. Это похоже на то, как мыльные пузыри приобретают сферическую форму, потому что такая форма минимизирует общую площадь поверхности, тем самым задействуя наименьшее количество энергии.
Математически этот вид капиллярной конденсации — то, как водяной пар из окружающего воздуха будет самопроизвольно конденсироваться внутри пористых материалов или между соприкасающимися поверхностями — обычно описывается уравнением, разработанным сэром Уильямом Томпсоном (лордом Кельвином) и впервые упомянутым в статье 1871 года. Это уравнение, которое оказалось удивительно точным вплоть до 10-нанометрового масштаба. Физиков интересовало, может ли оно описывать меньшие величины.
Типичная влажность для такого типа конденсации составляет от 30 до 50%, но при молекулярных масштабах 1 нанометр или меньше (молекула воды составляет около 0,3 нм в диаметре) только один или два молекулярных слоя воды могут поместиться внутри 1 нм. В таком масштабе уравнение Кельвина не имело смысла. Это может не иметь значения для строительства замков из песка, но капиллярная конденсация также актуальна для многих микроэлектронных, фармацевтических и пищевых производств. Гейм и его коллеги нашли способ преодолеть давние экспериментальные проблемы изучения капилляров на молекулярном уровне.
Ученые использовали вандерваальсовую сборку двумерных кристаллов для создания капилляров атомного масштаба и изучения конденсации внутри них. Маленькие капилляры имеют высоту менее четырех Ангстремов и могли вместить лишь монослой воды. Выяснилось, что и в таком масштабе макроскопическое уравнение Кельвина точно описывает конденсационный переход в сильно гидрофильных (слюдяных) капиллярах и остается качественно справедливым для слабогидрофильных (графитовых) капилляров.
В 2010 году Андре Гейм, выпускник МФТИ, получил Нобелевскую премию за открытие графена — двумерной кристаллической формы углерода, где атомы расположены в один слой.
См. также:
