Ещё одна аппроксимация полиномом функции нескольких переменных
В задачах интерполяции функций по заданным значениям функции для заданного набора аргументов широко применяется формула аппроксимации функции полиномом, совпадающего в заданных точках со значениями исследуемой функции.
Обобщим эту формулу на случай функции нескольких переменных
Скалярное произведение векторов будем вычислять с учётом квадратов дисперсий значений аргументов Dx
- с целью учета равнозначности каждой координаты аргумента вычисляем Dx[k] =M2[k] − M1[k]∗M1[k]
- < A; B > = SUM A[k] * B[k] / Dx[k]
Алгоритм
1. Для заданных векторов Xi рассчитываем вектор Dx квадратов дисперсий значений аргументов
2. Для вектора X находим p ближайших точек X1,…, Xp, где расстояния между точками вычисляется с учётом квадратов дисперсий значений аргументов
3. Вычисляем значение полинома P (X) = SUM Yi*П < X-Xj, Xi-Xj > / < Xi-Xj, Xi-Xj >, где скалярное произведение вычисляется с учётом квадратов дисперсий значений аргументов
Демонстрация аппроксимации для функции двух переменных
history.txt
- -1 -1 -10
- 1 1 10
- 0 0 0
- -1 1 -8
- 1 -1 -20
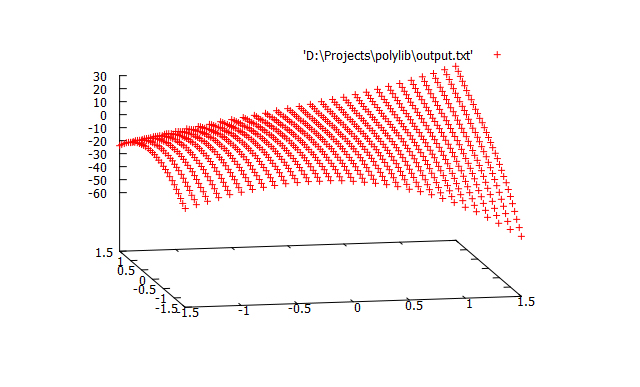
Построим график значений полинома на решётке с шагом 0.1 в программе gnuplot
- predict.exe -history history.txt -input input.txt -output output.txt -p 5
- splot «output.txt»
// predict.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
struct t_previous_result
{
std::vector x;
double y;
};
/////////////////////////////////////////////////////////
// Вычисление квадрата растояния между двумя векторами координат
double delta(std::vector& a, std::vector& b, std::vector& dx)
{
auto s = 0.0;
auto i = 0;
for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] - b[i]) * (a[i] - b[i]) / dx[i];
for (; i < a.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += a[i] * a[i] / dx[i];
for (; i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += b[i] * b[i] / dx[i];
return s;
}
/////////////////////////////////////////////////////////
// Вычисление растояния проекции двух векторов
double scalar(std::vector& a, std::vector& b, std::vector& dx)
{
auto s = 0.0;
auto i = 0;
for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] * b[i]) / dx[i];
return s;
}
/////////////////////////////////////////////////////////
// Возвращает предсказание для указанных параметров исходя из исторических данных
double predict(std::vector& x,
std::vector& previous_results,
std::vector& dx,
int p)
{
std::vector> neighbors;
for (auto it = previous_results.begin(); it != previous_results.end(); ++it)
{
std::vector& x2 = it->x;
auto d = delta(x, x2, dx);
std::pair pair(*it, d);
neighbors.push_back(pair);
}
std::sort(neighbors.begin(), neighbors.end(),
[](std::pair const& a, std::pair const& b)
{
return (a.second < b.second);
});
neighbors.resize(std::min(p, static_cast(neighbors.size())));
auto y = 0.0;
for (auto iti = neighbors.begin(); iti != neighbors.end(); ++iti)
{
auto s = iti->first.y;
std::vector& xi = iti->first.x;
for (auto itj = neighbors.begin(); itj != neighbors.end(); ++itj)
{
if (iti == itj) continue;
std::vector& xj = itj->first.x;
std::vector xxj;
std::vector xixj;
for (auto i = 0; i < x.size() && i < xj.size(); i++) xxj.push_back(x[i] - xj[i]);
for (auto i = 0; i < xi.size() && i < xj.size(); i++) xixj.push_back(xi[i] - xj[i]);
s *= scalar(xxj, xixj, dx) / scalar(xixj, xixj, dx);
}
y += s;
}
return y;
}
/////////////////////////////////////////////////////////
// Дефолтные значения
static const int _p = 3;
int main(int argc, char* argv[])
{
std::vector previous_results;
std::vector dx;
char* input_file_name = nullptr;
char* output_file_name = nullptr;
char* previous_results_file_name = nullptr;
auto p = _p;
std::string line;
// Поддержка кириллицы в консоли Windows
// Функция setlocale() имеет два параметра, первый параметр - тип категории локали, в нашем случае LC_TYPE - набор символов, второй параметр — значение локали.
// Вместо второго аргумента можно писать "Russian", или оставлять пустые двойные кавычки, тогда набор символов будет такой же как и в ОС.
setlocale(LC_ALL, "");
for (auto i = 1; i < argc; i++)
{
if (strcmp(argv[i], "-help") == 0)
{
std::cout << "Usage :\t" << argv[0] << " [-input ] [-output ] [...]" << std::endl;
}
else if (strcmp(argv[i], "-input") == 0) input_file_name = argv[++i];
else if (strcmp(argv[i], "-output") == 0) output_file_name = argv[++i];
else if (strcmp(argv[i], "-history") == 0) previous_results_file_name = argv[++i];
else if (strcmp(argv[i], "-p") == 0) p = atoi(argv[++i]);
}
if (input_file_name != nullptr) freopen(input_file_name, "r", stdin);
if (output_file_name != nullptr) freopen(output_file_name, "w", stdout);
if (previous_results_file_name != nullptr)
{
std::vector m1;
std::vector m2;
std::ifstream history(previous_results_file_name);
if (!history.is_open()) throw "Error opening file";
while (std::getline(history, line))
{
std::stringstream ss(line);
std::vector x;
std::copy(std::istream_iterator(ss), std::istream_iterator(),
std::back_inserter(x));
auto y = x.back();
x.pop_back();
t_previous_result previous_result;
previous_result.x = x;
previous_result.y = y;
previous_results.push_back(previous_result);
for (auto i = 0; i < x.size(); i++)
{
if (i >= m1.size()) m1.push_back(0.0);
if (i >= m2.size()) m2.push_back(0.0);
m1[i] += x[i];
m2[i] += x[i] * x[i];
}
}
for (auto it = m1.begin(); it != m1.end(); ++it) *it /= previous_results.size();
for (auto it = m2.begin(); it != m2.end(); ++it) *it /= previous_results.size();
for (auto i = 0; i < m1.size() && i < m2.size(); i++) dx.push_back(m2[i] - m1[i] * m1[i]);
}
while (std::getline(std::cin, line))
{
double y;
std::vector x;
std::stringstream ss(line);
std::copy(std::istream_iterator(ss), std::istream_iterator(),
std::back_inserter(x));
y = predict(x, previous_results, dx, p);
for (auto it = x.begin(); it != x.end(); ++it) std::cout << *it << ' ';
std::cout << y << std::endl;
}
return 0;
}
Интернет-адрес проекта: https://github.com/dprotopopov/polylib
Используемое программное обеспечение
- Microsoft Visual Studio 2013 — среда программирования
- gnuplot — кросс-платформенный инструмент для построения графиков www.gnuplot.info
