Доказательство с нулевым разглашением на примере реализации SRP в ProtonMail22.02.2023 11:01

Привет, Хабр! Это команда Eppie. Подробнее о нашем проекте бессерверной электронной почты можно почитать в этом посте.

Мы, параллельно с созданием собственного децентрализованного протокола, интегрируем в клиентское приложение Eppie популярные классические сервисы. Осенью мы познакомились с основателем Proton Энди Йеном и договорились добавить в Eppie возможность подключения почтового ящика ProtonMail. Насколько нам известно, ни один нативный десктопный клиент не умеет авторизоваться на сервере Proton — Eppie будет первым.

В Proton реализована собственная версия протокола SRP (Secure Remote Password). Наш криптограф портировал библиотеку на C#. Если хотите посмотреть код, вот ссылка на репозиторий в GitHub.

SRP — пример «доказательства с нулевым разглашением». Смысл процедуры в том, чтобы доказать факт владения определенной информацией, не раскрывая при этом саму информацию. В частности, аутентификация по SRP позволяет пользователю ProtonMail доказать, что он знает пароль, не передавая пароль серверу. Сейчас расскажем, как это устроено изнутри.

В статье будет несколько несложных формул, но текст не рассчитан на математиков и специалистов по безопасности. Здесь будет неформальный рассказ с некоторыми упрощениями для тех, кто хочет на уровне интуиции понять как устроены современные криптографические протоколы.

Немного теории

Со средней школы мы помним, что для любой математической операции существует обратная операция. Вычитание — обратная операция к сложению, деление — к умножению и так далее. С помощью обратной операции, зная результат и одно из слагаемых, можно получить второе слагаемое.

3 + 5 = 8

8 - 5 = 3

Теперь пусть слагаемые принадлежат конечному множеству чисел, и сложение производится по модулю N, который равен количеству элементов множества. Сумма по модулю равна остатку от деления суммы на значение модуля и тоже принадлежит этому множеству. Допустим, слагаемые принадлежат к группе целых чисел от 0 до 11. Множество состоит из 12 элементов, значит модуль равен 12.

$(9 + 4)\ mod\ 12 = 13\ mod\ 12 = 1$

Такое множество с заданной на ней операцией по модулю называют «конечной группой», а N — «порядком группы» (строго говоря, не любое множество может считаться конечной группой — должны выполняться некоторые обязательные условия, но мы не будем их разбирать, чтобы не усложнять рассказ).

Наглядный пример сложения в конечной группе — движение стрелки по циферблату. Будем считать, что на циферблате 12 делений от 0 до 11, и часовая стрелка всегда указывает на одно из делений, никогда не оказываясь между. Когда стрелка доходит до последнего элемента (11 часов), счет продолжается с нуля.

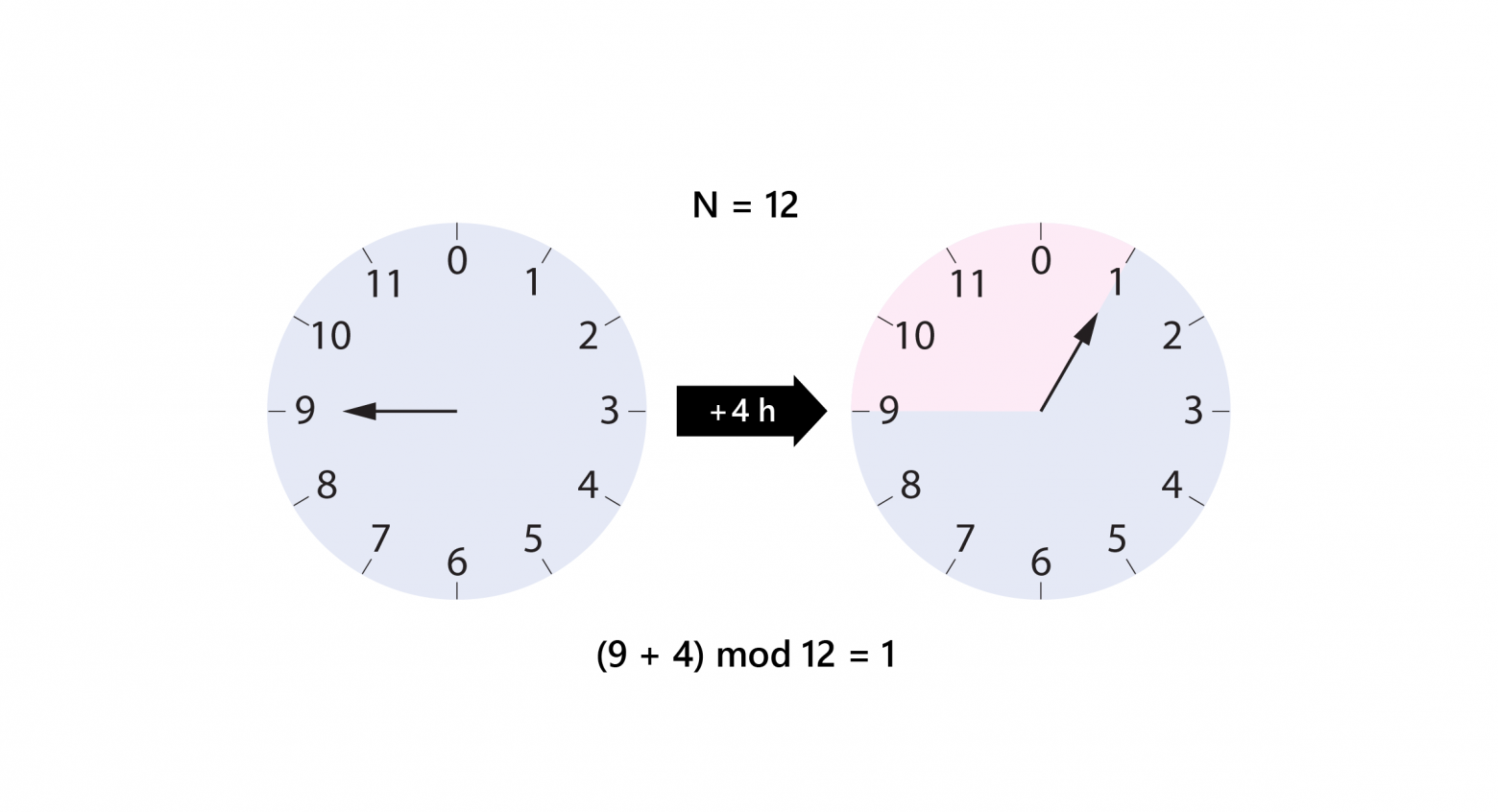Циферблат как конечная группа со сложением Циферблат как конечная группа со сложением

Для выполнения обратной операции в конечной группе со сложением нужно знать сумму по модулю, одно из слагаемых и значение модуля. Зная эти три параметра, мы все еще можем вычислить неизвестное слагаемое.

$(9 + x)\ mod\ 12 = 1 = (9 + x) - 12 ⋅ n$

Где n = 0 или 1 (по условию оба слагаемых принадлежат множеству, поэтому сумма не превышает 2N — 2)

$9 + x\ –\ 12 ⋅ 0 = 1$

— не может быть правильным ответом по условию (-8 не элемент группы)

$9 + x\ –\ 12 ⋅ 1 = 1$

— единственное решение в данной группе

Пока все просто. Теперь рассмотрим умножение. В конечной группе с умножением 0 исключается, a N должно быть простым числом. Пусть в новой группе N = 11, а в качестве множителей возьмем 6 и 9.

$(6 ⋅ 9)\ mod\ 11 = 54\ mod\ 11 = 10$

Попробуем найти неизвестный второй множитель:

$(6 ⋅ x)\ mod\ 11 = 10$

6 ⋅ x - 11 ⋅ n = 10

, где — целое число

Чтобы найти правильное значение x, будем подставлять все значения n от 0 до N-2, пока x не окажется положительным целым числом, принадлежащим группе. В данном случае x = 9 при n = 4.

Таким образом, в конечной группе с умножением обратная операция представляет собой «сложную вычислительную задачу», которую можно решить только самым неэффективным способом — полным перебором всех возможных вариантов n.

Еще одно важное свойство конечных групп — ассоциативность, или, как учат в школе, «результат не зависит от расстановки скобок»:

$((6 ⋅ 9) ⋅ 5)\ mod\ 11 = (6 ⋅ (9 ⋅ 5))\ mod\ 11$

Благодаря этим и некоторым другим особенностям, конечные группы часто используются в криптографии. Например, они лежат в основе протокола генерации совместного ключа Диффи-Хеллмана и протокола защищенной парольной аутентификации SRP.

Обмен ключами по протоколу Diffie-Hellman

Договоримся, что процесс шифрования в компьютере — это преобразование одного числа в другое с помощью математической операции. Можно сказать, что мы зашифровали число 3 прибавив к нему 7, и расшифровали его с помощью обратной операции. Число 7 в криптографии называется ключом. В этом примере — зная, что ключ равен 7, а результат шифрования — 10, можно получить исходное число 3.

Самая примитивная схема шифрования — «шифр Цезаря» — так и устроена: буквы в тексте смещаются на k позиций в алфавите. Так, если ключ k = 3, то »а» превращается в »г», «б» — в »д» и так далее. Позиции букв в алфавите — конечная группа со сложением по модулю. Модуль равен количеству букв в алфавите, поэтому «я» превратиться в «в». Один участник переписки прибавляет k к каждой букве в сообщении, а второй — расшифровывает его, отнимая то же число. Чтобы понимать друг друга, обе стороны должны были владеть одним и тем же ключом.

Такой способ шифрования называется симметричным. Его самое слабое звено — момент передачи ключа: ключ можно подслушать или украсть у человека, который везет его записанным на бумажке. Но до изобретения асимметричной криптографии в 70-х годах XX века других вариантов у нас не было. Симметричное шифрование используют и сейчас: например, когда бухгалтерия присылает вам по почте архив с паролем (пусть даже шифр устроен сложнее чем шифр Цезаря).

Асимметричная криптография позволяет не обмениваться ключами вовсе. Или точнее —позволяет участникам договориться о совместном секретном ключе и использовать его впоследствии для шифрования, обмениваясь только несекретной информацией. Подслушивающая сторона не может воспроизвести ключ, кроме как полным перебором всех вариантов.

Самый известный пример такой схемы — генерация совместного ключа по протоколу Диффи-Хеллмана. Метод основан на вычислениях в конечной группе.

Допустим, Алиса и Боб (традиционные имена из учебников по криптографии) хотят обмениваться зашифрованными сообщениями. Ева хочет узнать содержание их переписки, и для этого ей нужен ключ шифрования. Боб звонит Алисе, чтобы создать ключ. Ева прослушивает разговор с самого начала.

Алиса и Боб используют конечную группу с заданной на ней операцией умножения по модулю N. На практике это всегда число большого порядка, но пусть в нашем примере

Ева может узнать это число.

Дальше Алиса выбирает в группе случайное секретное число a, не сообщая его Бобу. А Боб выбирает случайное b. Эти числа называются «приватными ключами» Алисы и Боба, которые нельзя разглашать. Ева не должна их узнать. a и b должны быть больше 1 и меньше N — 1, иначе их легко будет найти. Предположим, что

Далее, Алиса и Боб выбирают «генератор» g — число из группы, обладающее определенными криптографическими свойствами, которые мы здесь опустим. Ева может узнать это число. Пусть в примере g = 3. Каждый участник возводит g в степень, равную своему приватному ключу.

Алиса вычисляет $3^{14} = 4782969$

Боб вычисляет $3^{11} = 177147$

Если бы на этом этапе Алиса и Боб сообщили друг другу свои результаты, Ева могла бы узнать секретные ключи с помощью логарифмирования (при условии, что вычисления ведутся с целыми числами):

$\log_3(4782969) = 14$

$\log_3(177147) = 11$

Но Алиса и Боб проводят вычисления в группе с умножением по модулю 17.В таком случае

$A = 3^{14}\ mod\ 17 = 2$

$B = 3^{11}\ mod\ 17 = 7$

A и B — «публичные», или «открытые» ключи. Алиса и Боб сообщают их друг другу. Не существует эффективного алгоритма, который позволит Еве вычислить приватный ключ, зная генератор, модуль и публичный ключ. В нашем примере N дает всего 16 вариантов для перебора, но, если N равно, например, $2^{1024}$ , перебор всех вариантов на самом мощном компьютере займет миллиарды лет.

Остался последний шаг: Алиса и Боб вычисляют совместный секретный ключ K, который они в дальнейшем и будут использовать для шифрования сообщений. Алиса возводит B (публичный ключ Боба) в степень, равную своему приватному ключу a по модулю N:

$K = B^a\ mod\ N = 7^{14}\ mod\ 17 = 8$

Боб делает то же самое с публичным ключом Алисы и своим приватным:

$K = A^b\ mod\ N = 2^{11}\ mod\ 17 = 8$

Совместный ключ K всегда совпадает, благодаря ассоциативности групповой операции.

$(g^a)^b = (g^b)^a = g^{ab}$

При замене обычного умножения (возведение в степень — частный случай умножения) на умножение по модулю это свойство сохраняется:

$g^{ab}\ mod\ N = g^{ba}\ mod\ N$

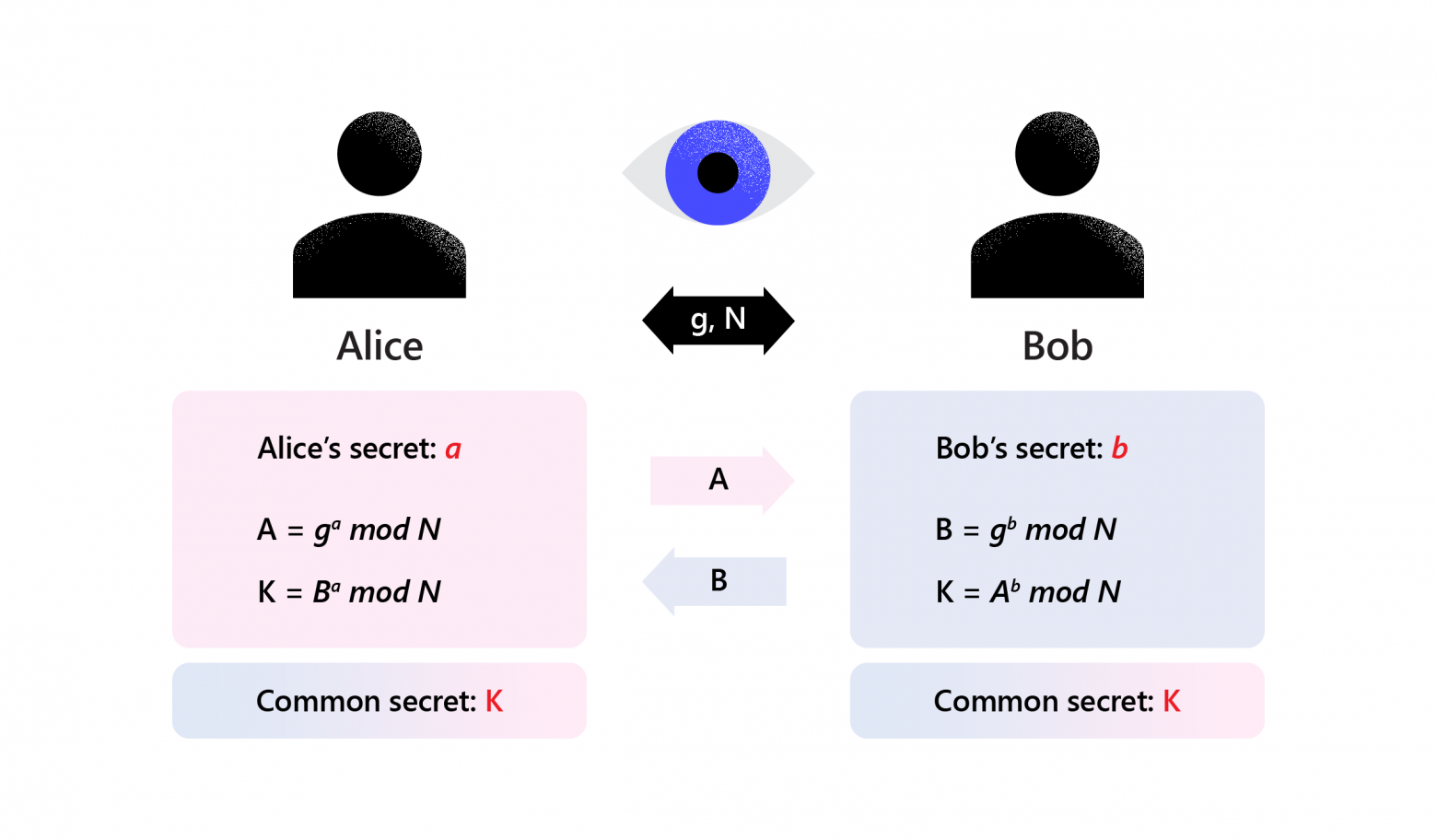Схема генерации совместного ключа по протоколу Диффи-Хеллмана

Теперь у Алисы и Боба есть совместный секретный ключ K, и они могут использовать его для шифрования сообщений. Для генерации совместного ключа каждый использовал свой приватный ключ и публичный ключ собеседника. Но Ева не может воспроизвести совместный секретный ключ не зная приватного.

Что не так с парольной аутентификацией

Отвлечемся ненадолго от асимметричной криптографии.

В наивной аутентификации сервер хранит оригиналы паролей. Когда пользователь хочет залогиниться, он вводит свой идентификатор (обычно имя пользователя или email) и пароль. Сервер находит пользователя в базе данных по идентификатору, сравнивает полученный пароль со своей копией, и, если пароли совпадают, авторизует пользователя.

Приличные сервисы не хранят пароли в открытом виде — их «солят» и «хешируют». Не вдаваясь в детали, скажем, что хеширование — это тоже математическая функция преобразования чисел. По хешу невозможно восстановить исходное значение, при этом из одних и тех же исходных данных всегда получается один и тот же хеш. Соль — это случайное число, с которым хешируют пароль, чтобы усложнить подбор. Когда новый пользователь заводит учетную запись, сервер сохраняет хеш пароля. Когда пользователь пытается залогиниться, сервер хеширует полученный пароль и сравнивает его со своей копией: когда хеши совпадают, считается, что совпадают пароли, и аутентификация пройдена успешно. Таким образом сервер авторизует пользователя, не храня пароль.

Но у этого подхода есть два больших недостатка. Во-первых, базу данных можно украсть и попытаться взломать перебором или словарной атакой. Если вдруг атакующая сторона знает ваше имя, девичью фамилию матери, любимые фильмы, книги, дату рождения, и вы были не слишком изобретательны в выборе пароля — ваши данные обречены. Вся нужная для взлома информация может храниться в той же базе данных, или в других, ранее украденных базах, в открытом виде. Достаточно одного совпадения, чтобы связать записи из разных украденных баз и получить материал для взлома пароля в автоматическом режиме.

Вторая проблема состоит в том, что безопасность ваших данных опирается на доверие к сервису. Что именно и как зашифровано в базе — неизвестно. Действительно ли сервис не может расшифровать ваш пароль? Нужен ли ему пароль для доступа к данным? Ответы на эти вопросы полностью зависят от добросовестности сервиса, и никак не зависят от вас.

Реализация SRP в ProtonMail

SRP (Secure Remote Password) — протокол парольной аутентификации, который позволяет пользователю вообще не отправлять пароль на сервер. Это пример «доказательства с нулевым разглашением» (zero knowledge proof): вы доказываете серверу, что знаете пароль, не раскрывая пароля.

Реализация протокола ProtonMail отличается от описанной в RFC. Далее будем рассматривать именно эту модифицированную версию.

На этапе регистрации клиентское приложение (браузер) вычисляет и отправляет на сервер так называемый «верификатор». При генерации верификатора используется пароль, но сам пароль никогда не попадает на сервер. Восстановить пароль, используя верификатор, невозможно.

В профиле пользователя на сервере ProtonMail хранится имя пользователя (идентификатор) I, верификатор v, соль s, модуль N, используемые для вычисления верификатора).

Для аутентификации используются следующие параметры:

Параметр	Создание	Хранение
N — модуль	За каждым пользователем закреплено свое значение N. Это 2048-битное целое число. Оно выбирается случайным образом из множества чисел, подготовленных специалистами ProtonMail	Хранится на сервере
g — генератор	В реализации Proton всегда равен 2
I — идентификатор (имя пользователя) клиента	Задан пользователем	Хранится на сервере
P — пароль клиента	Задан пользователем	Никуда не отправляется и нигде не хранится
s — соль	Выбирается клиентским приложением случайно и фиксируется для всех последующих вычислений	Хранится на сервере
x — вспомогательный параметр, играет роль приватного ключа	Хеш, генерируемый клиентом из пароля P, модуля N и соли s в процессе регистрации и каждый раз при аутентификации. Используется для вычисления верификатора	Никуда не отправляется и нигде не хранится
k — вспомогательный параметр	Хеш, генерируемый клиентом и сервером в процессе аутентификации из генератора g и модуля N	Не хранится
v — верификатор	v = gx mod N Генерируется пользователем в процессе регистрации и аутентификации	Хранится на сервере

Для хеширования используются алгоритм Bcrypt и модифицированная хеш-функция на основе SHA-512.

Обратите внимание на формулу вычисления верификатора. Она аналогична формуле вычисления публичного ключа в протоколе Диффи-Хеллмана.

В процессе аутентификации сервер и клиент выполняют следующие шаги:

Клиент отправляет на сервер свой идентификатор I
Сервер в ответ направляет клиенту «закреплённые» за ним параметры:
— модуль
— генератор
— соль
Клиентское приложение генерирует приватный ключ a из допустимого диапазона 2, …, N-2 и вычисляет публичный ключ $A = g^a\ mod\ N$ (A не равно нулю) и отправляет его на сервер.
Сервер генерирует приватный ключ b и вычисляет публичный ключ
$B = (kv + g^b )\ mod\ N$ (B не равно 0) и отправляет B клиенту.
Чтобы убедиться, что ни одну из сторон не подменили в процессе, клиент и сервер обмениваются проверочными значениями.
Клиент вычисляет следующие параметры:
— хеш от A и B
— см. таблицу
— см. таблицу
$S = (B - (k ⋅ g^x ))^{a + ux}\ mod\ N$ — предварительный общий секрет (premaster secret)
— хеш от значений A, B и S
Теперь клиент отправляет на сервер проверочное значение M1.
Сервер вычисляет проверочное значение M:
$S = (A ⋅ v^u))^b\ mod\ N$ — предварительный общий секрет (premaster secret)
— хеш от A, B и S
Если проверочные значения M и M1 совпадают, клиент успешно прошел проверку.
Затем аналогичный обмен проверочными сообщениями производится для того, чтобы клиент убедился в аутентичности сервера.
Сервер вычисляет проверочное значение для клиента:
— хеш, созданный из A, M1 и S
Это же значение вычисляется на стороне клиента, и если оно совпадает с полученным от сервера, аутентификация считается успешной.
После завершения процедуры на основе предварительного секрета S генерируется общий ключ шифрования K.

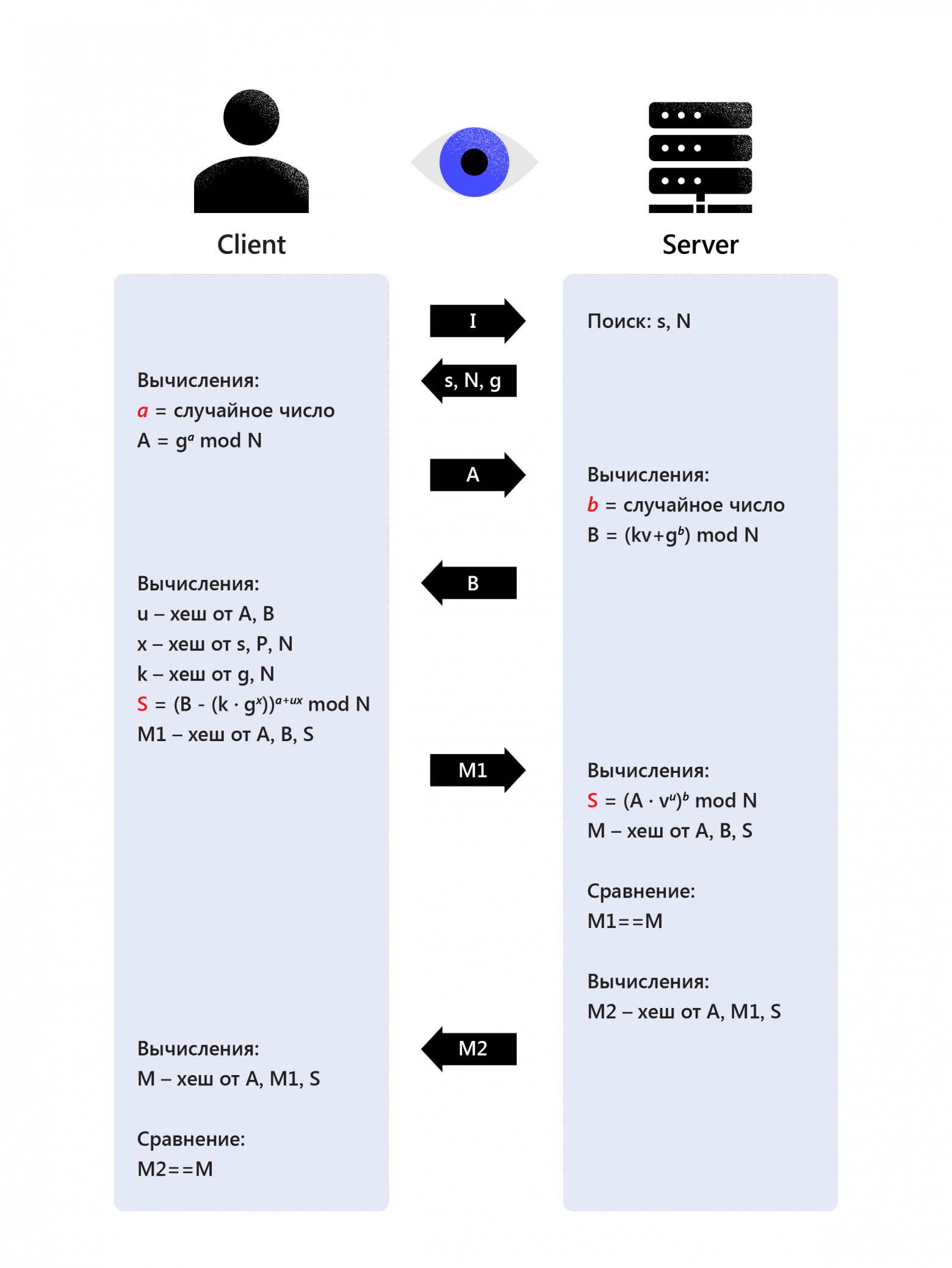Схема аутентификации по протоколу SRP на сервере ProtonMail Схема аутентификации по протоколу SRP на сервере ProtonMail

Суть описанных вычислений в том, что клиент и сервер, используя разные формулы, вычисляют одно и то же значение. Чтобы в этом убедиться, подставим в формулы S выражения для вычисления B, k и v.

Формула предварительного секрета, вычисляемая клиентом:
$S = (B - (k ⋅ g^x))^{a + ux}\ mod\ N$
Напомним, что
$B = (kv + g^b)\ mod\ N$
$v = g^x\ mod\ N$
Учитывая ассоциативность операций по модулю, уберем для читаемости модуль из уравнения:
$S = (kv + g^b - kv)^{a + ux} = g^{b(a + ux)}$
Формула предварительного секрета, вычисляемая сервером:
$S = (A ⋅ v^u)^b\ mod\ N$
При этом
$A = g^a\ mod\ N$
$v = g^x\ mod\ N$
$S = (g^a ⋅ (g^x )^u)^b = (g^{a + ux} )^b = g^{(a + ux)⋅b}$
$g^{b(a + ux)} = g^{(a + ux)b}$

Как видно из упрощения формул, S, вычисляемый на стороне клиента идентичен S, вычисляемому на сервере.

Используя метод обмена ключами, SRP закрывает самую заметную уязвимость серверной архитектуры: пароль не попадает в сеть, ни в открытом, ни в зашифрованном виде. Это большой шаг вперед по сравнению с привычной парольной аутентификацией.

Однако, использование SRP само по себе не гарантирует надежность компании. Пока в системе есть посредник с повышенными правами, уполномоченный хранить данные и авторизовать клиента, профиль пользователя остается, по сути, в собственности сервиса. Репутация ProtonMail не вызывает сомнений, но это скорее исключение, чем правило.

Принципиальное решение возможно в децентрализованной архитектуре, где факт владения приватным ключом и есть аутентификация. Никакие параметры не привязаны к профилю в базе данных — ни профиля, ни базы, ни сервера не существует. Децентрализованная почта, такая как Eppie, — это клиент без сервиса (в техническом понимании этого слова). Пользователь сам себя авторизует в p2p сети с помощью приватного ключа и является единственным владельцем своего почтового ящика. Никто кроме самого пользователя не несет ответственности за его данные, и он может быть уверен в своей приватности настолько, насколько он уверен в формулах, стоящих за шифрованием.

Если вас заинтересовал этот материал, подписывайтесь на наш блог на Хабре и задавайте вопросы в комментариях. И, конечно, записывайтесь на бета-тест Eppie.