Дипфейк видео по одному кадру27.05.2020 19:17

пример работы First Order Motion Model

Можно ли из одной фотографии сделать целый фильм? А записав движения одного человека, заменить его на другого в видео? Безусловно, ответ на эти вопросы, крайне важен для таких сфер как кинематограф, фотография, разработка компьютерных игр. Решением может стать цифровая обработка фотографии с помощью специализированного ПО. Задача, о которой идет речь, среди специалистов в этой области называется задачей автоматического синтеза видео или анимации изображения.

Для получения ожидаемого результата существующие подходы объединяют объекты, извлеченные из исходного изображения, и движения, которые могут поставляться в виде отдельного видео – «донора».

Сейчас, в большинстве сфер, анимация изображений осуществляется с помощью инструментов компьютерной графики. Для этого подхода требуются дополнительные знания об объекте, который мы хотим анимировать — обычно необходима его 3D модель (как сейчас это работает в кино индустрии можно почитать здесь). Большинство последних решений рассматриваемой задачи основывается на глубоком обучении моделей, в основе которых лежат генеративно-состязательные нейросети (GAN) и вариационные автоэнкодеры (VAE). Данные модели обычно используют предобученные модули для поиска ключевых точек объектов на изображении. Главная проблема такого подхода — данные модули способны распознавать только объекты, на которых они были обучены.

Как же решить описанную задачу для произвольных объектов, находящихся в кадре? Один из способов предложен в статье «First Order Motion Model for Image Animation». Авторы предлагают свою модель нейросети — First Order Motion Model, которая решает задачу анимации изображения без предобучения на анимируемом объекте. Обучившись на множестве видеороликов, изображающих объекты одной категории (например, лица, человеческие тела), разработанная авторами сеть позволяет анимировать все объекты, относящиеся к данной категории.

Подробнее разберемся как это работает…

Особенности решения

Для моделирования сложных движений используется набор энкодеров ключевых элементов объекта, обученных без учителя и локальные аффинные преобразования.

Для исключения из рассмотрения частей объекта, не видных на исходном изображении, применяется маска перекрытия (occlusion map). Так как эти части отсутствуют на изображении они должны быть сгенерированы нейросетью самостоятельно. Авторы также расширяют функцию эквивариантных потерь, используемую для обучения детектора ключевых точек, с целью улучшения оценки афинных преобразований.

Общая схема

Фреймворк состоит из двух основных модулей: модуля оценки движения и модуля генерации изображения. Модуль оценки движения предназначен для предсказания поля движения из кадра
$D \in \mathbb{R} ^{3×H×W}$ видео в исходное изображение $S ∈ \mathbb{R} ^{3×H×W}$ . Поле движения позже используется для выравнивания ключевых точек объектов из кадра $S$ в соответствие с позой этих объектов в кадре $D$ .

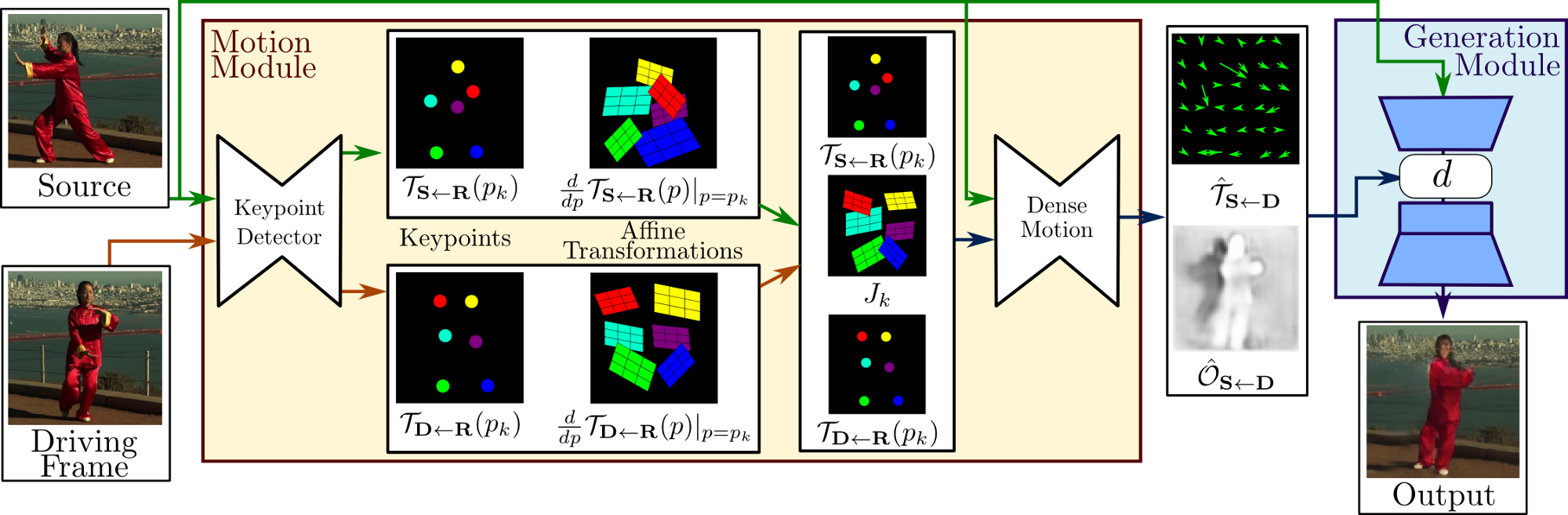
На вход детектору ключевых точек подаётся изображение $S$ и кадр $D$ из видео. Этот детектор извлекает представление движения первого порядка, состоящего из разреженных ключевых точек и локальных аффинных преобразований относительно абстрактного кадра (системы отсчета) $R$ . Сеть переноса движения использует такое представление движения для создания обратного оптического потока $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ из $D$ в $S$ и карту перекрытия $\hat{\mathcal{O}}_{\mathrm{S \leftarrow D}}$ . Исходное изображение и выходные данные сети переноса движения используются модулем генерации изображения для визуализации целевого изображения.

Далее рассмотрим особенности данного решения более подробно.

Локальные аффинные преобразования для приближения движения

Модуль оценки движения оценивает обратный оптический поток $\mathcal{T}_{\mathrm{S \leftarrow D}}$ от движущегося кадра $D$ до исходного кадра $S$ . Авторы аппроксимируют $\mathcal{T}_{\mathrm{S \leftarrow D}}$ разложением в ряд Тейлора в окрестности ключевых точек. Предполагается, что существует абстрактный кадр $R$ (система отсчета), поэтому оценка $\mathcal{T}_{\mathrm{S \leftarrow D}}$ выражается через оценки $\mathcal{T}_{\mathrm{S \leftarrow R}}$ и $\mathcal{T}_{\mathrm{R \leftarrow D}}$ . Более того, учитывая кадр результата $X$ , мы оцениваем каждое преобразование $\mathcal{T}_{\mathrm{X \leftarrow R}}$ в окрестности обученных ключевых точек. Рассмотрим разложение в ряд Тейлора в $K$ ключевых точках $p_1,..., p_K$ , где обозначают координаты ключевых точек в $R$ .

Получаем:

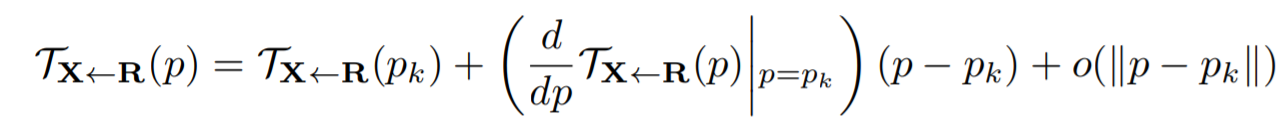
Чтобы оценить $\mathcal{T}_{\mathrm{R \leftarrow X}} = \mathcal{T}_{\mathrm{X \leftarrow R}}^{-1}$ , предполагаем, что $\mathcal{T}_{\mathrm{X \leftarrow R}}$ локально биективен в окрестности каждой ключевой точки.

Итого:

$\mathcal{T}_{\mathrm{S \leftarrow D}} = \mathcal{T}_{\mathrm{S \leftarrow R}} \circ \mathcal{T}_{\mathrm{R \leftarrow D}} = \mathcal{T}_{\mathrm{S \leftarrow R}} \circ \mathcal{T}_{\mathrm{D \leftarrow R}}^{-1}$

Предсказатель ключевых точек выдает $\mathcal{T}_{\mathrm{S \leftarrow R}}(p_k)$ и $\mathcal{T}_{\mathrm{D \leftarrow R}}(p_k)$ . Авторы используют стандартную архитектуру U-Net, которая оценивает $K$ тепловых карт, по одной для каждой ключевой точки.
Последний слой декодера использует softmax для предсказания тепловых карт, которые могут интерпретироваться как карты достоверности обнаружения ключевых точек.

Авторы используют сверточную нейросеть $P$ для оценки $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ с помощью $\mathcal{T}_{\mathrm{S \leftarrow D}}(z)$ в ключевых точках (здесь координаты ключевых точек обозначили через $z$ ), и исходный кадр $S$ . Важно, что параметры $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ , такие как края или текстура, выровнены попиксельно в соответствии с $D$ , а не с $S$ . Для того чтобы входные данные были уже выровнены с $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ , мы деформируем исходные кадры и получаем $K$ преобразованных изображений $S^0,...,S^k$ ( $S^0 = S$ ), каждое из которых выровнено относительно $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ в окрестности ключевой точки. Тепловые карты и преобразованные изображения $S^1,...,S^k$ объединяются и обрабатываются в U-Net.
$\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}(z)$ выражается формулой:

Здесь $M_k$ — маска для выделения окрестности контрольной точки для которой происходит это преобразование ( $M_0$ — для добавления фона) и $J_k$ выражается формулой:

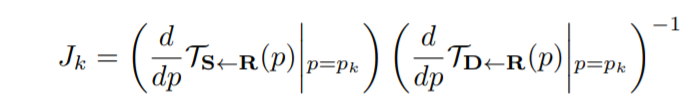
Генерация изображения

Напомню, что исходное изображение $S$ не выровнено попиксельно с создаваемым изображением $\hat{D}$ . Чтобы справиться с этим, авторы используют стратегию деформации объекта. После двух down-sampling блоков мы получаем карту объектов $\xi \in \mathbb{R}^{H' \times W'}$ . Затем мы деформируем $\xi$ в соответствии c $\hat{\mathcal{T}}_{\mathrm{S \leftarrow D}}$ . При наличии перекрытий в $S$ , оптического потока может быть недостаточно для генерации $\hat{D}$ . Здесь вводится понятие — карта перекрытий $\hat{\mathcal{O}}_{\mathrm{S \leftarrow D}} \in [0, 1]^{H' \times W'}$ , чтобы пометить области карты объектов, которые должны быть дорисованы, потому что они отсутствуют на изображении $S$ . Новая карта объектов выглядит так:

$\xi ' = \hat{\mathcal{O}}_{\mathrm{S \leftarrow D}} \odot f_w(\xi, \hat{\mathcal{T}}_{\mathrm{S \leftarrow D}})$

где $f_w(\cdot, \cdot)$ означает операцию обратной деформации, а $\odot$ — произведение Адамара (поразрядное логическое умножение соответствующих членов двух последовательностей равной длины).

Мы оцениваем маску перекрытия с помощью разреженного представления ключевых точек, добавляя канал к конечному слою сети переноса движения. $\xi '$ подается в последующие слои модуля генерации изображения, чтобы визуализировать получаемый кадр.

Функции потерь

Сеть тренируется непрерывно, комбинируя несколько функций потерь. Используется reconstruction loss, основанная на перцептивной функции потерь Джонсона. В качестве ключевой функции потерь для движений в кадре применяется пред-обученная сеть VGG-19. Формула reconstruction loss представлена ниже:

$L_{rec} (\hat{D}, D)= \sum_{i = 1}^I |N_i(\hat{D}) - N_i(D)|$

$\hat{D}$ — восстановленный кадр, $D$ — кадр с исходным движением, $N_i(\cdot)$ — i-ый элемент канала, извлеченный из конкретного слоя VGG-19, $I$ — количество каналов элементов в этом слое.

Наложение ограничения эквивариантности

Предсказатель ключевых точек не требует каких-либо знаний о ключевых точек во время обучения. Это может привести к нестабильным результатам. Ограничение эквивариантности является одним из наиболее важных факторов, определяющих нахождение ключевых точек без учителя. Это заставляет модель прогнозировать ключевые точки, которые не противоречат известным геометрическим преобразованиям. Поскольку модуль оценки движения не только предсказывает ключевые точки, но также и Якобианы, мы расширяем функцию потерь эквивариантности, чтобы дополнительно включить в нее ограничения на Якобианы.

Авторы предполагают, что изображение $X$ претерпевает пространственную деформацию $\mathcal{T}_{\mathrm{X \leftarrow Y}}$ , которая может быть как аффинным преобразованием, так и thin plane spline. После этой деформации мы получаем новое изображение $Y$ . Применяя расширенную оценку движения к обоим изображениям, получаем набор локальных аппроксимаций для $\mathcal{T}_{\mathrm{X \leftarrow R}}$ и
$\mathcal{T}_{\mathrm{Y \leftarrow R}}$ . Cтандартное ограничение эквивариантности записывается так:

$\mathcal{T}_{\mathrm{X \leftarrow R}} \equiv \mathcal{T}_{\mathrm{X \leftarrow Y}} \circ \mathcal{T}_{\mathrm{Y \leftarrow R}}$

После разложения в ряд Тейлора обеих частей уравнения мы получаем следующие ограничения (здесь $\mathbb{1}$ — единичная квадратная матрица):

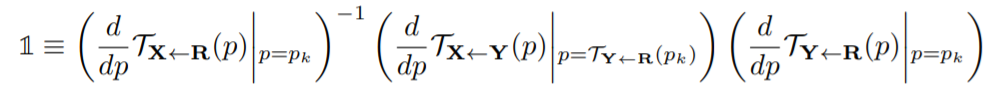
Для ограничения положений ключевых точек используется функция $L_1 $ . Авторы используют равные веса при объединении функций потерь во всех экспериментах, так как модель не чувствительна к относительным весам reconstruction loss и 2х эквивариантных функций потерь.

Анимация

Для анимации объекта из исходного кадра $S_1$ с помощью кадров видео $D_1, . . . D_T$ каждый кадр $D_t$ самостоятельно обрабатывается, чтобы получить $S_t$ . Для этого в кадр $S_1$ передается относительное движение между $D_1$ и $D_t$ . То есть, мы применяем преобразование $\mathcal{T}_{\mathrm{D_t \leftarrow D_1}}(p)$ в окрестности каждой точки $p_k$ :

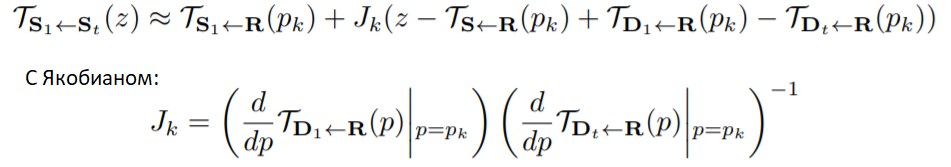
Важно заметить, что в связи с этим возникает ограничение — объекты на кадрах $S_1$ и $D_1$ должны иметь похожие позы.

Модель ставит рекорды!

Модель обучалась и тестировалась на 4 различных наборах данных:

VoxCeleb — датасет лиц из 22496 видео, взятых из YouTube;
UvA-Nemo — датасет для анализа лиц, состоящий из 1240 видео;
BAIR robot pushing — датасет, состоящий из видео, собранных роботизированной рукой Сойера, которая кладет разные предметы на стол. В нем 42880 обучающих и 128 тестовых видео.
280 TaiChi видео из YouTube.

Результаты работы сравнивались с X2Face и Monkey-Net, так как они являются единственными существующими решениями для анимации изображений без предварительного моделирования.

Как видно из таблицы, First Order Motion модель превосходит другие подходы по всем показателям.

Долгожданные примеры

Mgif

Fashion

А теперь попробуйте сами! Это совсем просто, все подготовлено здесь.