Детектирование частей тела с помощью глубоких нейронных сетей07.05.2018 14:33

Привет, Хабр!

Сегодня я расскажу вам про один из методов решения задачи pose estimation. Задача состоит в детектировании частей тела на фотографиях, а метод называется DeepPose. Этот алгоритм был предложен ребятами из гугла еще в 2014 году. Казалось бы, не так давно, но не для области глубокого обучения. С тех пор появилось много новых и более продвинутых решений, но для полного понимания необходимо знакомство с истоками.

Обзор задачи

Давайте сначала вкратце про постановку задачи. У вас есть фотографии, на которых присутствует человек (один или несколько), и хочется на этих фото разметить части тела. То есть сказать, где находятся руки, ноги, голова и так далее.

Где бы такая разметка могла пригодиться? Первое же, что приходит на ум, это видеоигры. Можно играть в свою любимую RPG, размахивая виртуальным мечом, а не кликая мышкой. Для этого достаточно уметь лишь распознавать движения ваших рук.

Конечно, есть и куда более практичные применения. Например, отслеживание того, как покупатели в магазине кладут товары себе в корзину, а иногда ставят обратно на полочку. Тогда можно автоматически отслеживать, что купил посетитель, и необходимость в кассах исчезнет. Amazon уже реализовал эту идею в своих магазинах AmazonGo.

Думаю, приведенные примеры использования уже достаточно интересны, чтобы взяться за решение задачи. Однако, если у вас есть оригинальные идеи того, где еще можно применить рассмотренные концепты, смело пишите их в комментариях.

Обзор классики

Как решать эту задачу без нейронных сетей? Можно представить скелет человека в виде графа, где вершинами будут суставы, а ребрами — кости. А дальше придумать какую-нибудь математическую модель, которая будет описывать вероятность появления того или иного сустава в конкретном месте изображения, а также будет учитывать, насколько реалистично эти суставы расположены по отношению друг к другу. Например, чтобы ваша левая пятка не находилась на вашем же правом плече. Хотя, не исключаю того, что есть способные на это люди.

Один из вариантов такой мат. модели реализован во фреймворке pictorial structures model еще в 1973 году.

Но можно подойти к решению задачи и менее хитрым способом. Когда нам дают новую картинку, давайте просто искать в нашем исходном наборе размеченных картинок похожую и выдавать ее разметку. Если у нас изначально будет не очень много различных поз людей, то этот метод вряд ли взлетит, но, согласитесь, реализовать его не представляет труда. Для поиска похожих картинок тут обычно используют классические методы извлечения фич из области обработки изображений: HOG, дескриптор Фурье, SIFT и другие.

Есть и другие классические подходы, но здесь я не буду на них останавливаться и перейду к основной части поста.

Новый подход

Общая идея

Как вы уже могли догадаться, авторы статьи DeepPose (Alexander Toshev, Christian Szegedy) предложили своё решение с использованием глубоких нейронных сетей. Они решили рассмотреть эту задачу как задачу регрессии. То есть, для каждого сустава на фотографии нужно определить его координаты.

Предобработка данных

Далее я продолжу описание модели на более формальном языке. Но для этого необходимо ввести некоторые обозначения. Для удобства буду придерживаться нотаций авторов.

Обозначим входное изображение как $x$ , а вектор позы как $y = (\ldots, y_i, \ldots), \; i \in \{1, \ldots, k\}$ , где $y_i$ содержит координаты $i$ -го сустава. То есть мы сейчас представляем скелет человека графом из $k$ вершин. Тогда размеченное изображение будет обозначаться как $(x, y) \in D$ , где $D$ — наш тренировочный датасет.

Поскольку картинки могут иметь разный размер, а также люди на фотографиях могут быть представлены в разных масштабах и находиться в различных частях кадра, то было решено использовать ограничивающие области (bounding box, AABB), которые бы выделяли нужную область изображения (тело человека целиком или что-то более детальное, если нас интересует конкретная часть тела). Относительно центра такой области можно также считать нормализованные координаты внутренних точек. В самом тривиальном случае, областью может быть вся исходная картинка.

Обозначим bounding box с центром в точке $b_c \in \mathbb{R}^2$ , шириной $b_w$ и высотой $b_h$ тройкой чисел $b = (b_c, b_w, b_h)$ .
Тогда нормализованный вектор позы $y$ относительно области $b$ можно записать так

$N(y_i, b) = \left(\begin{matrix} 1/b_w & 0 \\ 0 & 1/b_h \end{matrix}\right) (y_i - b_c)$

То есть мы вычли из всех координат центр нужной области, а затем поделили $x$ -координату на ширину прямоугольника, а $y$ -координату на высоту. Теперь все координаты стали лежать в интервале от $-0.5$ до $0.5$ включительно.

Наконец, за $N(x; b)$ обозначим обрезание исходной картинки $x$ ограничивающей областью $b$ . Тривиальный бокс, который равен исходной картинке, обозначим за $b_0$ .

Если мы теперь возьмем функцию $\psi(x; \theta) \in \mathbb{R}^{2k}$ ( $x$ — входное изображение, $\theta$ — параметры модели, $k$ — количество определяемых суставов), которая по $x$ выдает нормализованный вектор позы, то вектор позы в исходных координатах $y^*= N^{-1}(\psi(N(x); \theta); b_0)$ .

В качестве функции $\psi$ у нас выступает нейронная сеть, веса которой описываются $\theta$ . То есть мы подаем на вход трехканальное изображение фиксированного размера, а получаем на выходе $k$ пар координат суставов:

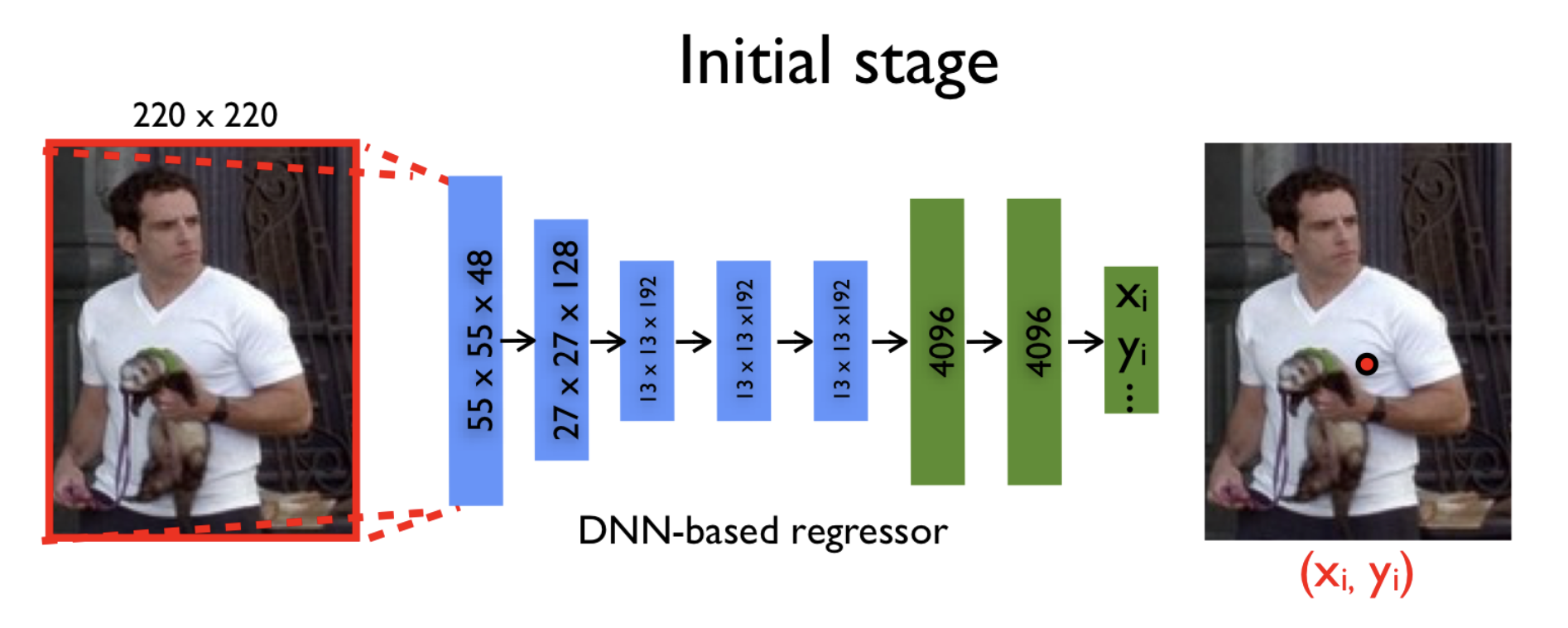
Казалось бы, уже на данном этапе мы можем взять какую-нибудь глубокую нейронную сеть (например, AlexNet, которая отлично себя показала на задаче классификации изображений, выиграв соревнование ImageNet в 2012 году), и обучить ее регрессии. Найдем такие параметры модели, чтобы минимизировать сумму квадратов отклонений предсказанных координат от истинных. То есть идеальные параметры $\theta^*= \arg\min_{\theta} \sum\limits_{(x, y) \in D_N} \sum\limits_{i=1}^{k} ||y_i - \psi(x; \theta)||^2_2$ . Таким образом, мы пытаемся восстановить исходные координаты суставов независимо друг от друга.

Каскад сетей

Однако, поскольку на вход нейронная сеть принимает картинку фиксированного размера (а именно, $220 \times 220$ пикселей), часть информации теряется, если картинка изначально была в лучшем разрешении. Поэтому у модели нет возможности проанализировать все мелкие детали изображения. Модель «видит» всё в крупном масштабе и может попытаться восстановить позу лишь приблизительно.

Можно было бы просто увеличить размер входа, однако вместе с этим пришлось бы увеличить и без того немаленькое число параметров внутри сетки. Напомню, что классическая архитектура AlexNet содержит более 60 миллионов параметров! Версия модели, описанная в этой статье, — более 40 миллионов.

Компромиссом в желании подавать на вход картинку в хорошем разрешении и в необходимости сохранить адекватное число параметров стало использование каскада нейронных сетей. Что это значит? Сначала по исходной картинке, сжатой до $220 \times 220$ пикселей, предсказываются приблизительные координаты суставов, а каждая последующая нейронная сеть уточняет эти координаты уже по новой картинке. Эта новая картинка — не что иное, как некоторая нужная часть предыдущей (та самая ограничивающая область вокруг предсказаний с предыдущего этапа), тоже приведенная к размеру $220 \times 220$ .

Благодаря такому способу, последовательность моделей с каждым шагом наблюдает картинки все более высокого разрешения, что позволяет модели сосредоточиться на мелких деталях и поднять качество предсказаний.

Авторы используют одну и ту же архитектуру сети на каждом этапе (всего этапов $S$ ), однако обучают их отдельно. Давайте обозначим параметры сети на этапе $s \in \{1, \ldots, S\}$ за $\theta_s$ , а саму модель, предсказывающую координаты суставов, за $\psi(x; \theta_s)$ .

На начальном этапе ( $s = 1$ ) мы используем ограничивающую область $b_0$ (исходную картинку полностью) для предсказания приблизительных координат суставов:

$\texttt{Stage 1}: \: y^1 \leftarrow N^{-1}(\psi(N(x; b^0); \theta_1); b^0)$

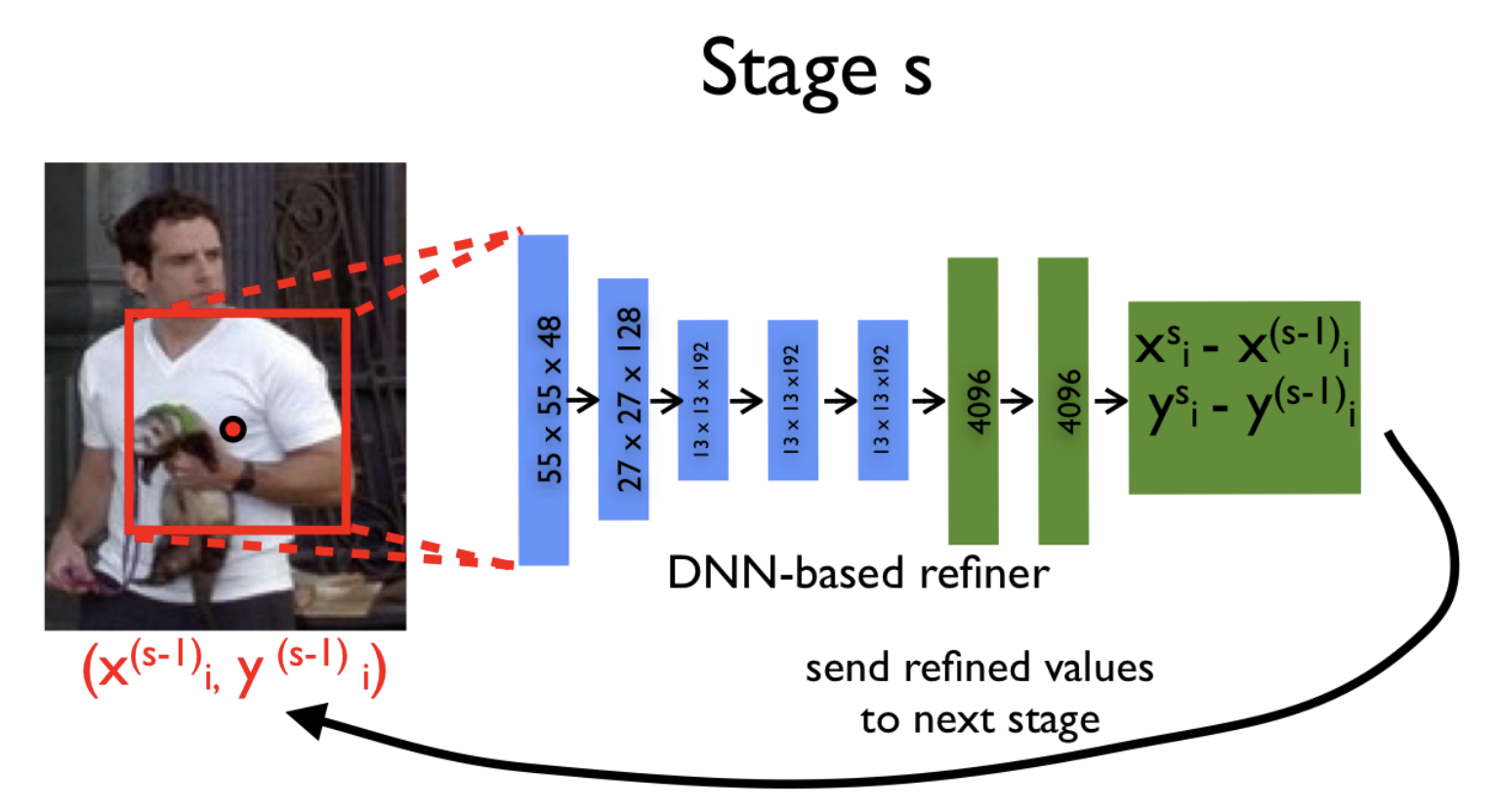
Далее, на каждой новой итерации ( $s = 2 \ldots S$ ) и для каждого сустава $i \in \{1, \ldots, k\}$ мы уточняем его координаты $y^{s-1}_i$ с помощью модели $\psi(x; \theta_s)$ :

$\texttt{Stage s}: \: y^s_i \leftarrow y^{(s - 1)}_i + N^{-1}(\psi_i(N(x; b^{(s - 1)}_i); \theta_s); b^{(s - 1)}_i) \\ b^s_i \leftarrow (y^s_i, \sigma \operatorname{diam}(y^s), \sigma \operatorname{diam}(y^s))$

Генерация данных

И уже теперь мы могли бы приступить к обучению такой модели, если бы не одно но. Обучение сложной нейронной сети, а тем более каскада сетей, требует большого количества сэмплов (размеченных изображений, в нашем случае). Например, AlexNet обучали на ImageNet-е, который состоит из 15 миллионов размеченных картинок размером $256 \times 256$ . Но даже такой датасет Алекс и его команда увеличивали более чем в 2048 раз, путем выбора случайных подызображений меньшего размера и их зеркальных отображений.

Чтобы в рассматриваемой задаче небольшой размер датасета не стал серьезной проблемой, важно было придумать хороший способ аугментирования данных, который бы подошел для каскада сетей.

Однако и тут авторы нашли довольно изящное решение. Вместо того, чтобы использовать предсказания координат суставов только с предыдущего этапа, они предложили генерировать эти координаты самостоятельно. Это можно сделать, сместив координаты $i$ -го сустава на вектор, сгенерированный из двумерного нормального распределения $\mathcal{N}^{(s - 1)}_i$ со средним и дисперсией, равными среднему значению и дисперсии наблюдаемых отклонений $y^{s - 1}_i$ от $y_i$ по всем примерам из тренировочной выборки.

Таким образом, мы моделируем работу предыдущих слоев на якобы новых картинках. Классная особенность этого метода заключается в том, что мы не ограничены сверху каким-то фиксированным количеством изображений, которые мы можем сгенерировать. Однако же, если их будет очень много, то они будут сильно похожи друг на друга, а следовательно, это перестанет приносить пользу.

Датасеты

Для задачи pose estimation существуют два известных открытых датасета, которые исследователи часто используют в своих научных работах:

Frames Labeled In Cinema (FLIC)

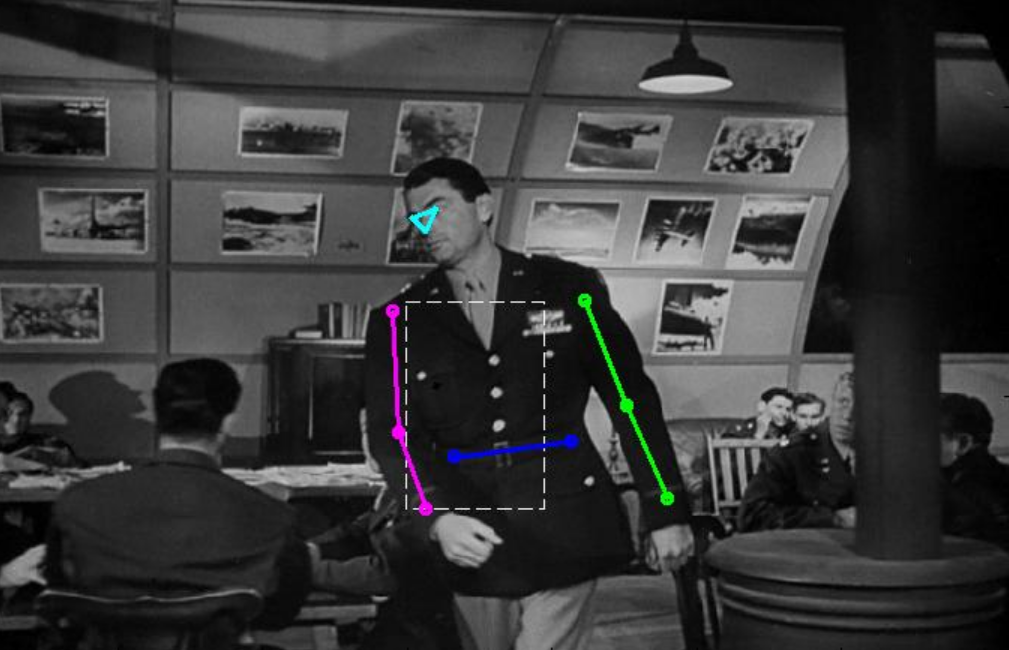
Название этого датасета говорит само за себя. Он представляет собой 5000 аннотированных кадров из различных фильмов. Для каждой картинки нужно предсказать координаты 10 суставов.

Leeds Sports Pose Dataset (LSP)

Этот датасет состоит из фотографий людей, занимающихся спортом. Однако, не по всем фотографиям у вас сложится о нем правильное представление:

Но это скорее исключения, а типичные примеры с разметкой выглядят так:
Этот датасет содержит уже 12000 изображений. От FLIC он отличается тем, что здесь нужно предсказывать координаты 14 точек вместо 10.

Метрики

Последнее, с чем нам осталось разобраться, это понять, как оценивать качество полученной разметки. Авторы статьи в своей работе использовали сразу две метрики.

Percentage of Correct Parts (PCP)

Это процент корректно распознанных частей тела. Под частью тела подразумевается пара суставов, которые соединены между собой. Мы считаем, что корректно распознали часть тела, если расстояние между предсказанными и реальными координатами двух суставов не превышает половину ее длины. Как следствие, при одной и той же ошибке результат детекции будет зависеть от расстояния между суставами. Но, несмотря на этот недостаток, метрика является довольно популярной.

Percent of Detected Joints (PDJ)

Для компенсации минусов первой метрики, авторы приняли решение использовать еще одну. Вместо того, чтобы считать количество правильно распознанных частей тела, было решено смотреть на количество корректно предсказанных суставов. Это избавляет нас от зависимости от размеров частей тела. Сустав считается корректно распознанным, если расстояние между предсказанными и реальными координатами не превышает значения, зависящего от размера тела на картинке.

Эксперимент

Напомню, что вышеописанная модель состоит из $S$ этапов. Однако, мы пока так и не уточнили, как выбирается эта константа. Чтобы подобрать хорошие значения для этого и других гиперпараметров, в статье было взято 50 картинок из обоих датасетов в качестве валидационной выборки. Так авторы остановились на трех этапах ( $S=3$ ). То есть по начальному изображению мы получаем первое приближение позы, а затем дважды делаем уточнение координат.

Начиная со второго этапа, было сгенерировано по 40 изображений для каждого сустава из реального примера. Например, таким образом для LCP датасета (где предсказываем 14 различных суставов), с учетом зеркальных отображений, получается $11000 \times 40 \times 2 \times 14 \approx 12$ миллионов примеров! Еще стоит отметить, что для FLIC в качестве исходного bounding box $b_0$ использовались ограничительные прямоугольники, полученные детектирующим человека алгоритмом. Это позволяло заранее отсекать ненужные части изображения.

Первая нейросеть в каскаде обучалась приблизительно на 100 машинах в течение 3 дней. Однако утверждается, что точность, достаточно близкая к максимальной, была достигнута уже за первые 12 часов. Каждая из моделей на следующих этапах обучалась уже по 7 дней, поскольку работала с датасетом, который в 40 раз превосходил по размеру оригинальный.

Результаты

Далее на графиках можно увидеть точность распознавания кистей и локтей на разных этапах модели. По оси $x$ — значение трешхолда в метрике PDJ (если разность предсказанных и настоящих координат меньше трешхолда, считаем, что сустав определен верно). Из графиков видно, что дополнительные этапы дают существенное улучшение точности.

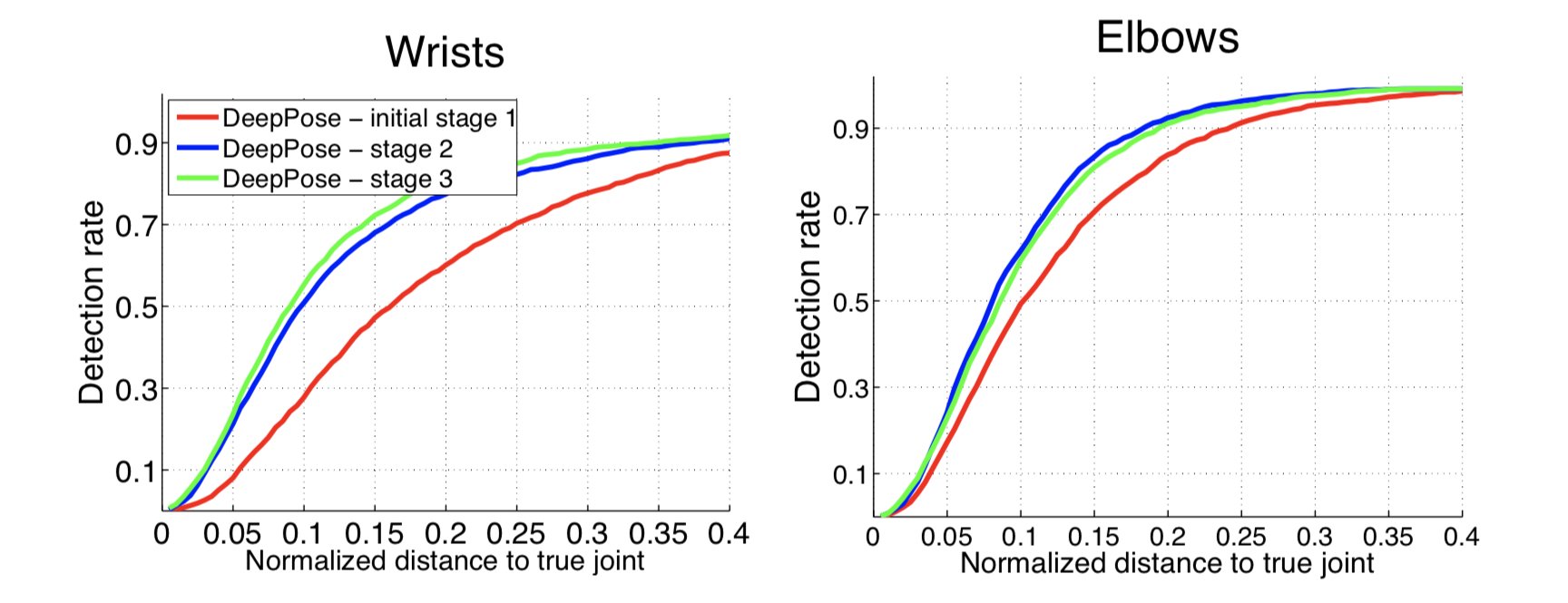
Интересно также посмотреть, как уточняет координаты каждая последующая нейронная сеть. На изображениях ниже зеленым цветом нарисована истинная поза, а красным — поза, предсказанная моделью.

Еще приведу сравнения результатов данной модели с другими пятью state-of-the-art алгоритмами того времени.

Выводы

На мой взгляд, из интересного в этой работе можно выделить способ построения модели, где путем последовательного соединения нескольких нейронных сетей одинаковой архитектуры получилось неплохо увеличить точность. А также метод генерации дополнительных примеров с целью расширения тренировочного датасета. Считаю, что задумываться над вторым стоит всегда, когда вы работаете с ограниченным набором данных. И чем больше способов аугментации вы знаете, тем проще придете к нужному именно вам.

Пост написан совместно с avgaydashenko.