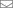Дешевый как автобус, удобный как такси: перспективный вид общественного транспорта для больших и средних городов. Часть222.04.2023 12:01

(Jean-Claude Mézières)

ссылка на «Часть1: Предварительный анализ

Эксперименты на торе.

Это вторая часть работы, посвященной исследованию новых схем движения общественного транспорта. В первой мы рассмотрели простейшую беспересадочную, и основанную на ней схему с одной пересадкой, которые могут быть реализованы в клеточном городе на плоскости. В этой части моделью города станет клеточный город на «плоском» торе. У тора, в отличие от прямоугольника, нет края, кроме того, положения всех точек на нем абсолютно равнозначны. Из-за отсутствия края и (транзитивной) симметричности расчёты для тороидального города получаются проще, а численные результаты — почти такими же, как и для прямоугольного города на плоскости. Два этих обстоятельства делают тороидальный клеточный город идеальной испытательной площадкой для новых схем движение пассажирского транспорта. В настоящей статье мы разберем две таких схемы на торе, а в следующей вернемся на плоскость и приспособим полученные здесь результаты для использования в реалистичных условиях прямоугольного города.

Содержание этой работы не является самостоятельным и предполагает знакомство с первой частью статьи. Для понимания главы 2 вам потребуется уровень математики, соответствующий примерно программе первых двух курсов университета, для всего остального — должно хватить и школьной. Во время чтения полезно иметь под рукой карандаш и лист бумаги. Если ваш браузер отображает формулы неправильно, попробуйте несколько раз обновить страницу.

1. Евклидов тор.

1.1 Прямоугольник с зеркальной телепортацией.

Возьмем прямоугольный лист бумаги $\Pi$ и положим его перед собой так, чтобы можно было говорить о его верхнем, нижнем, правом, и левом краях. Далее, представим, что по поверхности $\Pi$ могут перемещаться воображаемые нарисованные человечки. Для этих человечков установим следующее правила телепортации:

1) всякий раз, когда какой-то человечек пересекает верхнюю границу листа в некоторой ее точке $A$ , он тут же телепортируется в зеркально симметричную точку $A’$ на нижней границе листа, и наоборот;

2) всякий раз, когда какой-то человечек пересекает правую границу листа в некоторой ее точке $B$ , он тут же телепортируется в зеркально симметричную точку $B’$ на левой границе листа, и наоборот;

(рисунок 1)

Что будет, если человечек попробует выйти за границу листа через его угол, например через верхний левый? В этом случае мы будем считать, что человечек пересекает сразу две стороны листа: верхнюю и левую, поэтому на него действуют оба правила 1) и 2). Легко проверить, что при любом порядке действий этих правил результат будет один: человечка из левого верхнего угла перенесется в нижний правый.

1.2 Геометрическая интерпретация.

Телепортациия между противоположными краями прямоугольника $\Pi$ может быть реализована наглядно. Для этого сперва сведем нижний край листа $\Pi$ с верхним и склеим их, в результате у нас получится полый цилиндр. Далее этот цилиндр нужно значительно сплюснуть, согнуть баранкой и подклеить друг к другу его торцы. Если все сделано правильно, то в итоге получится тор $T$ . Линия склейки верхнего края листа с нижним будет на этом торе одной из его параллелей, а линия склейки правого края с левым — одним из его меридианов. Движение всякого человечка на исходном листе бумаги $\Pi$ теперь можно рассматривать, как его движение на склеенном из этого листа торе $T$ , и наоборот. При таком сопоставлении телепортация человечка между двумя противоположными сторонами $\Pi$ происходит в точности тогда, когда его движение на торе $T$ пересекает линию склейки этих сторон. Из-за этой двойственности мы будем говорить, что прямоугольный лист с зеркальной телепортацией $\Pi$ является представлением тора $T$ . Кроме того, поскольку каждый малый участок, вырезанный из поверхности $T$ , можно выложит на плоскость, сам тор $T$ мы будем называть плоским.

(рисунок 2)

Выше мы уже говорили о меридианах и параллелях тора, давайте дадим этим понятиям хотя бы полуформальное определение. Пусть $\Pi$ — это прямоугольник с зеркальной телепортацией, $T$ — склеенный из него тор. Всякий отрезок $I$ на $\Pi$ , концы которого лежат на сторонах $\Pi$ , мы будем называть сквозным. Среди всех сквозных отрезков только у строго вертикальных и строго горизонтальных концы связаны между собой правилом телепортации. Такие отрезки при склейке листа в тор превратятся в окружности. Горизонтальные сквозные отрезки на $\Pi$ и получающиеся из них окружности на $T$ мы назовем параллелями тора, а вертикальные сквозные отрезки на $\Pi$ и образуемые ими окружности на $T$ -его меридианами.

1.3 Главные карты.

Склеим из прямоугольного листа $\Pi$ плоский тор $T$ и нанесем на его поверхность какой-нибудь рисунок. Если затем мы аккуратно разрежем клеевые швы, то получим исходный лист бумаги, который теперь несет на себе «разрезанный» рисунок с тора. В этом смысле исходный лист бумаги $\Pi$ можно считать такой же картой поверхности тора $T$ , какие человечество использует для изображения, например поверхности Земли. Разрезать тор можно не только вдоль его клеевых швов. В результате различных разрезаний могут получаться разные поверхности и разное число цельных компонент.

Упражнение. Попробуйте разрезать тор так, чтобы у вас получилось дважды перекрученное бумажное кольцо. Постарайтесь найти такое разрезание, которое дает два бумажных кольца, соединенных в двухзвенную цепь (фрагмент елочной гирлянды). Бумажное кольцо, которое перекручено всего один раз — есть лента Мебиуса. Подумайте, можно ли ленту Мебиуса вырезать из тора.

В тех случаях, когда в результате разрезания тора получается единый плоский лист, этот лист мы будем называть его картой. Конечно, не все карты тора будут иметь прямоугольную форму. Карты, которые получены разрезанием тора вдоль некоторого его меридиана и некоторой его параллели (то есть параллельно клеевым швам), мы будем называть главными. Должно быть очевидно, что всякая главная карта является прямоугольной.

Пусть $M$ — это (одна из) главная карта тора $T$ . Каждая точка $P$ на карте $M$ изображает собой единственную точку $p$ на торе $T$ . Для внутренних точек карты $M$ такое соответствие является взаимно-однозначным. В то же время если точка $P$ лежит на какой-либо из сторон $M$ , то сама $P$ и зеркально симметричная ей точка $P’$ на противоположной стороне $M$ (такие пары точек мы будем называть сопряженными) изображают одну и ту же точку $p$ на $T$ . В частности, все четыре угловые точки карты $M$ являются разными изображениями точки пересечения той параллели и того меридиана тора $T$ , разрезанием вдоль которых карта $M$ была получена.

Из самого определения главных карт следует, что каждый меридиан и параллель на них будет выглядеть как сквозной отрезок с сопряженными концами. Мы будем предполагать, что все главные карты ориентированы в пространстве так, что параллели на них являются горизонталями, меридианы — вертикалями, а направления вверх-вниз, вправо-влево на всех из них совпадают.

Легко проверить, что для любой точки $O$ на торе существует в точности одна главная карта, на которой $O$ лежит строго по центру. Эту карту мы будем обозначать как $M_O$ и говорить о ней, как о главной карте, центрирована в точке $O$ .

1.4 Преобразования одной главной карты тора в другую.

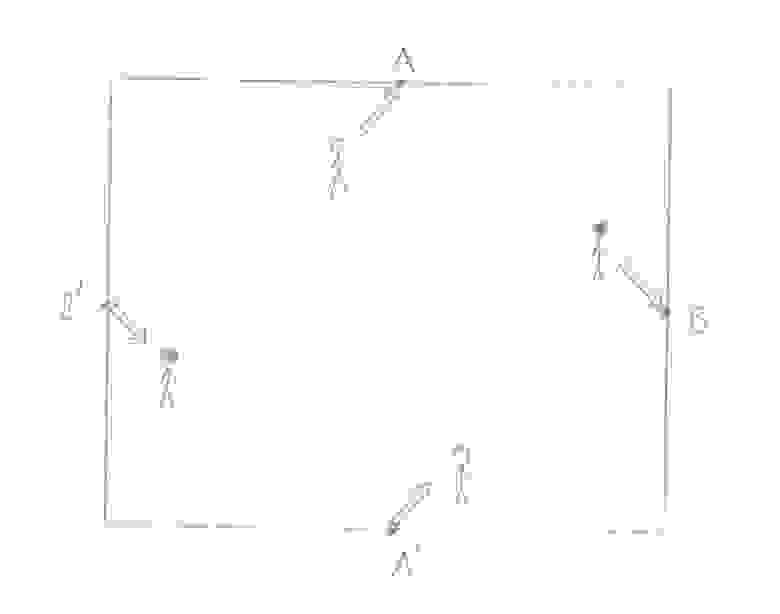
То обстоятельство, что все главные карты есть результат разрезания тора вдоль его параллелей и меридианов, дает нам ключ к пониманию, как из одной главной карты получить другую. Представим, что у нас есть две главные карты $M’$ и $M’’$ тора $ T$ . Пусть первая получена разрезанием тора $T$ вдоль его параллели $p’$ и меридиана $m’$ , а вторая — разрезанием вдоль параллели $p’’$ и меридиана . На карте $M’’$ изображением параллели будет являться множество всех точек нижнего и верхнего края , изображением меридиана $m’'$ — множество всех точек ее левого и правого края. Что касается карты $M’$ , то в общем случае параллель $p’’$ и меридиан $m’’$ будут изображены на ней как «рядовые» горизонтальный и вертикальный сквозные отрезки.

(рисунок 3)

Чтобы превратить карту $M’$ в карту $M’’$ достаточно выполнить следующие действия:
1) Разрезать $M’$ вдоль параллели $p’’$ , поменять местами нижний и верхний отрезы, а затем склеить их. Получившийся лист также будет главной картой, обозначим ее как $M^*$ . Нижней и верхней границей $M^*$ как и карте $M’’$ будет служить параллель $p’’$ , а меридиан , как и на карте $M’$ , будет ее внутренним сквозным отрезком. Остается
2) Разрезать $M^*$ вдоль меридиана поменять местами правый и левый отрезы, после чего снова их склеить. Результатом этих действий как раз и будет карта $M’’$ .

1.5 Кривые на торе.

Обсудим, как главные карты изображают кривые (непрерывные линии) на поверхности тора.
Пусть $M$ — это главная карта плоского тора $T$ , а $\gamma^M$ — произвольная кривая на $M$ . Если мы склеим противоположные края $M$ , то превратим ее обратно в $T$ , при этом кривая $\gamma^M$ станет кривой на торе. Таким образом о каждой кривой на главной карте $M$ можно говорить и как о кривой на поверхности тора $T$ . В обратную сторону последнее утверждение не верно, так как не всякая кривая на поверхности $T$ после его преобразования в главную карту $M$ превратится в кривую на $M$ .

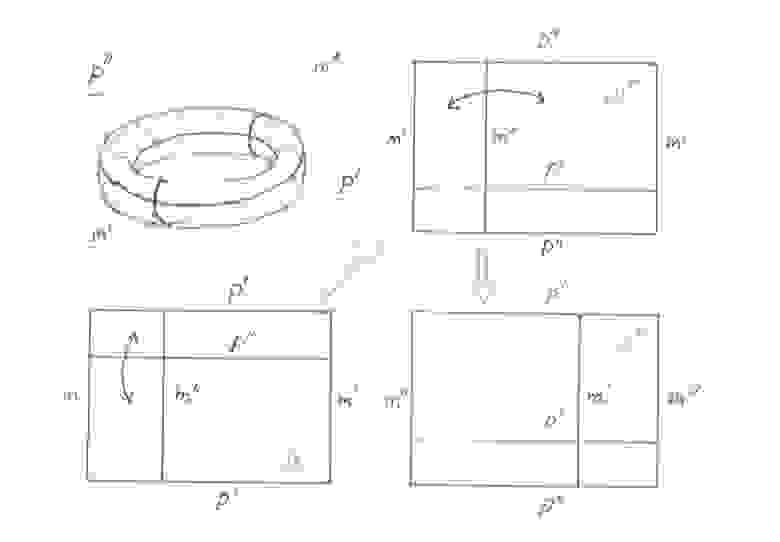
Пусть $M$ должна быть получена разрезанием $T$ вдоль его параллели $p$ и меридиана $m$ . Рассмотрим произвольную кривую $\gamma^T$ на поверхности тора $T$ . Точки пересечения $\gamma^T$ с линиями будущих разрезов $p$ и $m$ разбивают ее на последовательность сегментов ${\gamma}_1, … {\gamma}_N$ . Каждый из этих сегментов после разрезания $T$ станет самостоятельной кривой на $M$ , а их последовательность будет обладать тем свойством, что точка начала каждой следующей кривой будет сопряжена с точкой конца предыдущей. На этот раз обратное утверждение тоже верно: всякая последовательность ${\gamma^M}_1, … {\gamma^M}_N$ кривых на $M$ , в которой точка начала каждой следующей кривой сопряжена с точкой конца предыдущей, после склейки карты $M$ в тор $T$ превратится в некоторую единую кривую $\gamma^T$ на поверхности $T$ . Именно в этом смысле мы будем говорить, что последовательность кривых ${\gamma}_1, … {\gamma}_N$ задает кривую $\gamma^T$ на $T$ .

(рисунок 4)

Для произвольной кривой $\gamma$ на поверхности плоского тора произвольного меридиана $m$ и параллели $p$ мы можем построить проекцию множества точек $\gamma$ на $p$ вдоль $m$ , обозначим ее как $\gamma^p$ и проекцию $\gamma$ на m вдоль $p$ , которую мы обозначим как $\gamma^m$ . Множества $\gamma^p$ и $\gamma^m$ будут представлять собой либо отрезки на $p$ и $m$ , либо полностью совпадать с $p$ или $m$ . Длину \gamma^p мы назовем шириной или горизонтальным размахом кривой $\gamma$ , соответственно длину $\gamma^m$ — ее высотой или ее вертикальным размахом. Из свойств параллельных следует, что определение горизонтального и вертикального размаха не зависят от выбора конкретного $p$ и $m$ .

При проектировании схем пассажирского транспорта, мы всегда будем стремиться к тому, чтобы каждое путешествие на этом транспорте занимало как можно меньше времени. Этой цели нельзя достичь, если не позаботится, чтобы маршруты путешествий на таком транспорте были в некотором смысле кратчайшими кривыми между точками их начала и конца, либо кривыми, близкими к кратчайшим. Давайте попробуем разобраться, как выглядят кратчайшие кривые плоского тора, в частности, как они изображаются на его главных картах.

1.6 Кратчайшие на торе.

В опросе о кратчайших маршрутах нас будут интересовать два случая: кратчайшие маршруты среди всех кривых тора и кратчайшие маршруты среди так называемых «ступенчатых» кривых. Ступенчатыми мы будем называть такие ломанные, у которых каждый сегмент является либо горизонтальным, либо вертикальным отрезком (кусочком параллели или меридиана тора).

Кратчайшим маршрутом из точки $A$ в точку $B$ в классе всех кривых на плоскости, или внутри прямоугольника является, как известно, (направленный) отрезок $AB$ (вспомните почему). Чтобы сформулировать, какие маршруты на плоскости являются кратчайшими в классе ступенчатых кривых, заметим, что каждый ступенчатый маршрут задает определенное направление на каждом своем прямолинейном сегменте. Нетрудно проверит, что на плоскости или внутри прямоугольника ступенчатый маршрут $\gamma$ является кратчайшим тогда и только тогда, когда все его горизонтальные сегменты ровно как и все его вертикальные сегменты направлены в одну сторону (смотрите параграф 4.4 части 1). Например, если точка $B$ лежит выше и правее точки $A$ , то кратчайшими ступенчатыми маршрутами из $A$ в $B$ будут в точности те, у которых каждый горизонтальный сегмент «смотрит» вправо, а вертикальный — вверх (все ступеньки «ведут» вправо вверх).

Если плоскость снабжена декартовыми координатами с горизонтальной осью $Ox$ и вертикальной осью $Oy$ , то написанный выше критерий кратчайшести можно переформулировать еще одним интересным способом. Произвольный маршрут $\gamma$ мы будем называть монотонным, если движение точки вдоль \gamma сопровождаться (нестрого) монотонным изменением ее координат $x$ и $y$ . Попробуйте убедится, что на координатной плоскости ступенчатый маршрут $\gamma$ будет кратчайшим тогда и только тогда, когда он является монотонным. Длина всякой монотонной ступенчатой кривой с концами $A$ и $B$ равна сумме длин вертикальной и горизонтальной составляющих (проекций) вектора $\vec {AB}$ .

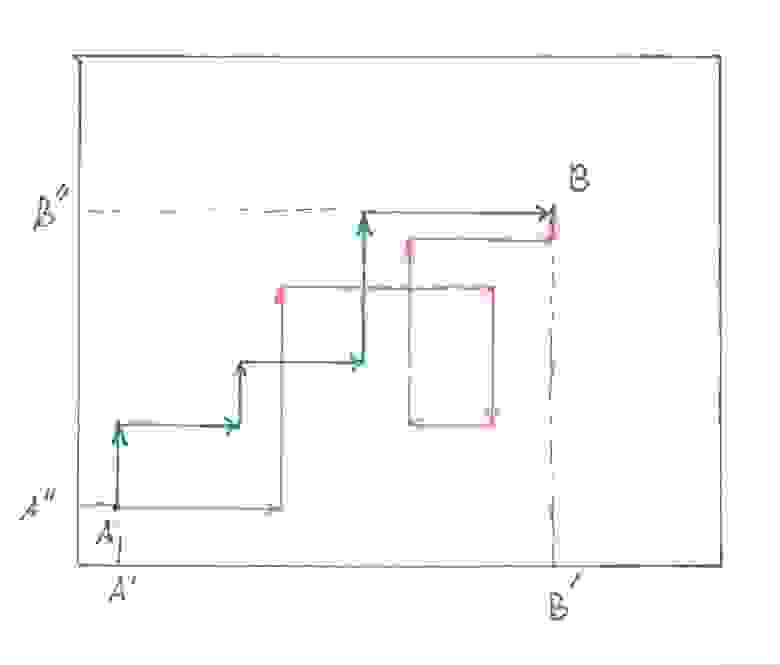
(рис 5)

На плоском торе $T$ с кратчайшими дела обстоят немного немного сложнее. Так, если в качестве представления тора взять прямоугольный лист $\Pi$ c зеркальной телепортацией между краями, то на нем можно указать такие пары точек $A$ и $B$ , что путь из $A$ в $B$ , состоящий из двух или даже трех отрезков и телепортаций между их концами будет короче, чем отрезок $AB^{\Pi}$ .

(рис 6)

К счастью, при помощи особого выбора главной карты вопрос о построении кратчайших на торе можно сильно упростить. Оказывается, что если $M_A$ — это главная карта тора $Т$ , центрированная в его точке $A$ , то для любой точки $B$ , кратчайший маршрут, который соединяет $A$ и $B$ на $M_A$ будет является в том числе и кратчайшим маршрутом, который соединяет $A$ и $B$ на $T$ и наоборот: каждый кратчайший маршрут между $A$ и $B$ на $T$ будет изображен на карте $M_A$ как ее кратчайшая между $A$ и $B$ . Сказанное одинаково верно и для маршрутов, кратчайших в классе всех кривых, и для маршрутов, кратчайших в классе ступенчатых. В частности, кратчайшая линия на торе между $A$ и $B$ будет изображена на карте $M_A$ в виде отрезка $AB^{M_A}$ , точнее, в виде отрезка, соединяющего точку $A$ c одной из тех точек $B^{M_A}$ , которые изображают $B$ на карте $M_A$ . Кратчайшая ступенчатая кривая на торе с концами $A$ и $B$ будет изображена на $M_A$ , как одна из монотонных ступенчатых кривых между $A$ и (одним из изображений) $B$ . Обоснование у этих утверждений такое:

Кратчайший на торе путь из точки $А$ в точку $B$ на карте $M_A$ выглядит либо как обычная кривая $\gamma$ , либо как кривая с телепортациями $\gamma_1 *... * \gamma_k$ . То, что второй случай, по сути, невозможен (только если все $\gamma_i$ кроме $\gamma_1$ состоят из одной точки) легко доказывается индукцией по $k$ .

Если $k = 1$ , то и доказывать нечего.
При $k = 2$ на карте $M_A$ у нас есть две кривые: $\gamma_1$ и $\gamma_2$ , склеенные между собой одной телепортацией. Используя ваши знания в школьной геометрии, покажите, что, как в классе всех кривых так и в классе ступенчатых, замена $\gamma_1$ и $\gamma_2$ на одну кратчайшую для $M_A$ кривую из $A$ в $В$ , точно не сделает путь между точками $A$ и $B$ длиннее.

(рис 7)

Пусть $k = N > 2$» /> и <img src= — это представление картой $M_A$ кратчайшего пути из $A$ в $B$ . Обозначим конец сегмента $\gamma_1$ как $O_1$ , начало $\gamma_2$ — как $O_2$ , конец $\gamma_2$ — как $O_3$ . Поскольку любой отрезок кратчайшего пути, очевидно, сам является кратчайшим путем, склейка из сегментов $\gamma_1$ и $\gamma_2$ — будет двухсегментной кратчайшей между точкой $A$ и точкой $O_3$ . Но раз так, то мы можем воспользоваться доказанным для $k=2$ утверждением и заменить путь $\gamma_1 * \gamma_2$ односегментным путем $\gamma_2'$ такой же или меньшей длины. Сделав это, мы получим путь $\gamma_2’ *... * \gamma_N$ , который соединяет $A$ и $B$ , состоит только из $(N-1)$ сегмента и имеет длину не больше, чем путь $\gamma_1 *... * \gamma_N$ , то есть являться кратчайшим.

1.7 Малые прямоугольники.

Пусть $A$ и $B$ — это две произвольные точки на поверхности тора, которые не лежат на одном меридиане или одной параллели, $m_A$ и $p_A$ — единственные меридиан и параллель, проходящие через точку $A$ , $m_B$ и $p_B$ — единственные меридиан и параллель, проходящие через точку $B$ . Вместе кривые $m_A$ , $p_A$ , $m_B$ и $p_B$ разбивают поверхность тора на 4 (связные) области, каждая из которых при подходящем выборе главной карты будет изображена на ней как прямоугольник.

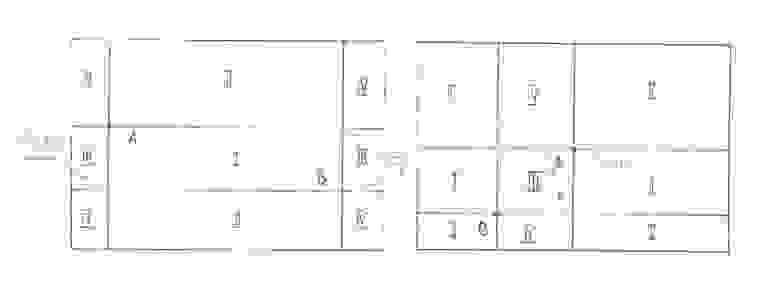
(рис 8)

В общем случае только у одного из этих 4-ех прямоугольников длина каждой из горизонтальных сторон будут меньше, чем полпараллели, а длина каждой вертикальной — меньше, чем пол меридиана. Этот (в общем случае) единственный прямоугольник мы будем называть малым прямоугольником, натянутым на точки $A$ и $B$ , и обозначать как $\Pi (AB)$ .

Полезность понятия малого прямоугольника заключается в следующем. Какова бы не была точка $B$ на поверхности тора, на карте $M_A$ прямоугольник $\Pi (AB)$ будет изображен как единая фигура. Рассмотрим тот случай, когда малый прямоугольник, натянутый на $A$ и $B$ всего один. Очевидно, что всякая кратчайшая кривая между $A$ и $B$ внутри $\Pi (AB)$ , будь то в классе ступенчатых или всех кривых, является кратчайшей в том же классе на карте $M_A$ и наоборот. Поскольку множество кратчайших кривых между $A$ и $B$ на торе, совпадает с множеством кратчайших кривых, построенных между этими точками на карте $M_A$ , то все эти кривые являются кратчайшими внутри $\Pi (AB)$ . Таким образом малые прямоугольники дают нам возможность рассуждать о кратчайших на торе, не обращаясь к его картам.
.
.
.