Deep (Learning+Random) Forest и разбор статей02.07.2019 12:04

Продолжаем рассказывать про конференцию по статистике и машинному обучению AISTATS 2019. В этом посте разберем статьи про глубокие модели из ансамблей деревьев, mix регуляризацию для сильно разреженных данных и эффективную по времени аппроксимацию кросс-валидации.

Алгоритм Глубокий лес: An Exploration to Non-NN Deep Models based on Non-Differentiable Modules

Zhi-Hua Zhou (Nanjing University)
Презентация
Статья
Реализации — ниже

Профессор из Китая рассказал про ансамбль деревьев, который авторы называют первым глубоким обучением на недиффиеренцируемых модулях. Это может показаться слишком громким заявлением, но этот профессор и его H-index 95 — приглашенные докладчики, этот факт позволяет отнестись к заявлению серьезнее. Основная теория Deep Forest разрабатывается давно, оригинальная статья аж 2017 года (почти 200 цитирований), но авторы пишут библиотечки и каждый год улучшают алгоритм по скорости. И сейчас, похоже, достигли того уровня, когда эта красивая теория может, наконец, быть применена на практике.

Общий вид архитектуры Deep Forest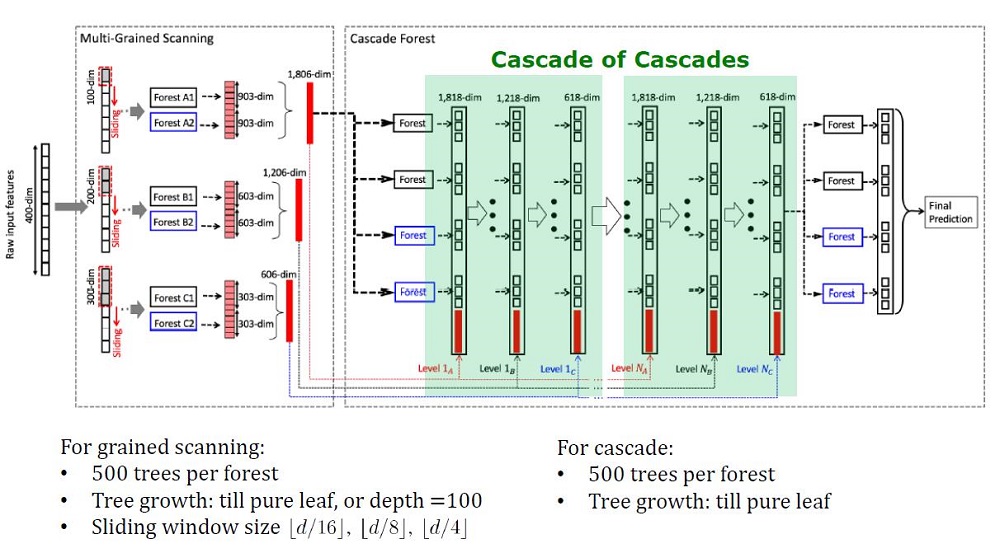

Предпосылки

Глубокие модели, под которыми сейчас подразумеваются глубокие нейросети, используются, чтобы уловить сложные зависимости в данных. Причем оказалось, что увеличение количества слоев более эффективно, чем увеличение числа unitов на каждом слое. Но у нейросетей свои минусы:

Требуется много данных, чтобы не переобучиться,
Нужно много вычислительных ресурсов, чтобы обучиться за разумное время,
Слишком много гиперпараметров, которые сложно настроить оптимально

Кроме того, элементы глубоких нейросетей — это дифференцируемые модули, которые не обязательно эффективны для каждой задачи. Несмотря на сложность нейросетей, концептуально простые алгоритмы, вроде случайного леса, часто работают лучше или не сильно хуже. Но для таких алгоритмов нужно вручную конструировать фичи, что тоже сложно сделать оптимально.

Уже и исследователи заметили, что ансамбли на Kaggle: «very poverfull to do the practice», и вдохновившись словами Шолле и Хинтона про то, что дифференцирование — самая слабая сторона у Deep Learning, решили создать ансамбль деревьев со свойствами DL.

Слайд «Как сделать хороший ансамбль»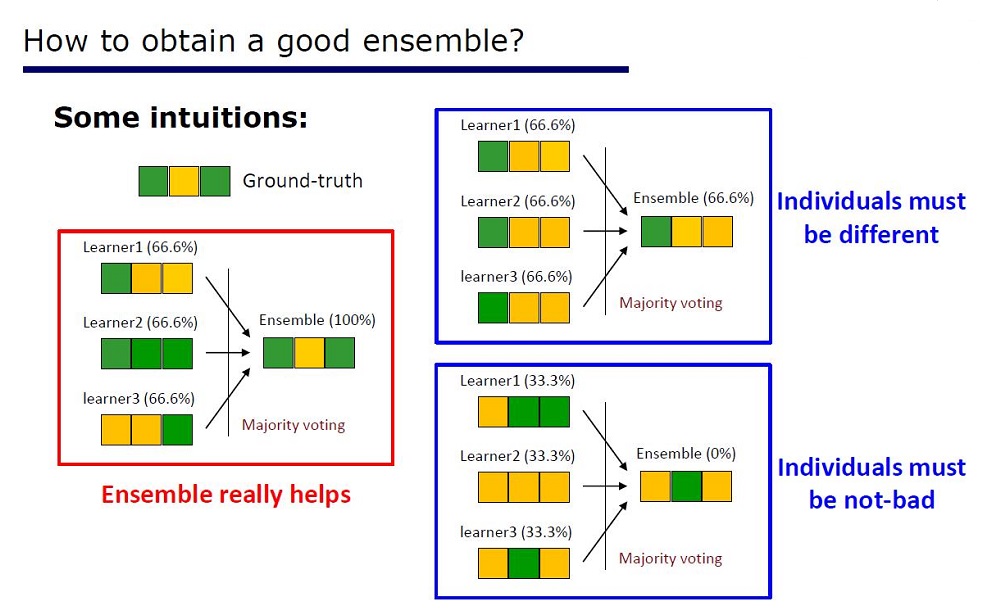

Архитектуру выводили из свойств ансамблей: элементы ансамблей должны быть не очень плохими по качеству и отличаться.

GcForest состоит из двух этапов: Cascade Forest и Multi-Grained Scanning. Причем, чтобы каскад не переобучался, он состоит из 2 типов деревьев — один из которых абсолютно рандомные деревья, которые можно применять на неразмеченных данных. Количество слоев определяется внутри алгоритма по кросс-валидации.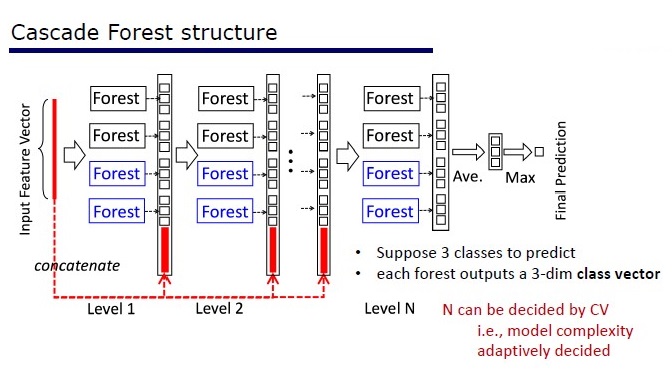

Два вида деревьев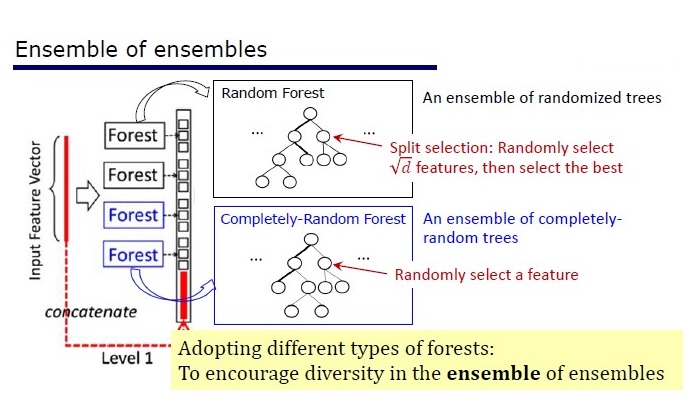

Результаты

Кроме результатов на стандартных датасетах авторы попробовали применить gcForest на транзакциях китайской платежной системы для поисков фрода и получили F1 и AUC гораздо выше, чем у LR и DNN. Эти результаты есть только в презентации, но код для запуска на некоторых стандартных датасетах есть на Git.

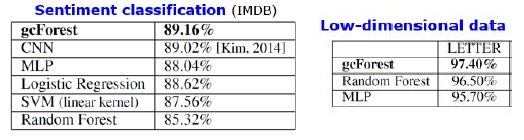
Результаты ставнений алгоритмов. mdDF — это optimal Margin Distribution Deep Forest, вариант gcForest

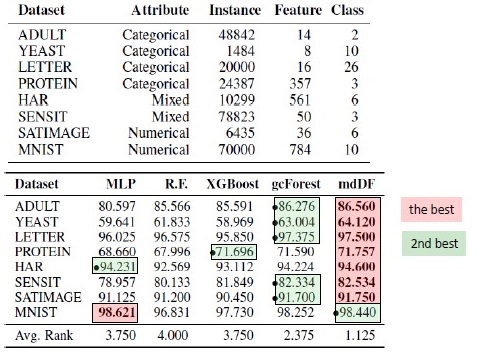
Плюсы:

Мало гиперпараметров, количество слоев настраивается автоматически внутри алгоритма
Параметры по умолчанию подобраны так, чтобы работать хорошо на многих задачах
Адаптивная сложность модели, на небольших данных — небольшая модель
Не нужно задавать фичи
Работает сравнимо по качеству с глубокими нейросетями, а иногда и лучше

Минусы:

Не ускоряется на GPU
На картинках проигрывает DNNs

У нейросеток есть проблема затухания градиента, а у глубокого леса проблема «затухания различности» (Diversity vanishing). Так как это ансамбль, то чем больше «разных» и «неплохих» элементов использовать — тем выше качество. Проблема в том, что авторы уже перебрали почти все классические подходы (сэмплирование, рандомизация). Пока в теме «различности» не появится новых фундаментальных исследований, будет сложно улучшить качество глубокого леса. Но сейчас возможно улучшить скорость вычислений.

Воспроизводимость результатов

Такой крутой выигрыш в качестве у XGBoost на табличных данных заинтриговал, и захотелось воспроизвести результат. Я взяла датасет Adults и применила GcForestCS (немного ускоренная версия GcForest) с параметрами от авторов статьи и XGBoost с параметрами по умолчанию. В примере, который был у авторов, фичи категориальные уже были как-то предобработаны, но не указано как. В итоге я использовала CatBoostEncoder и другую метрику — ROC AUC. Результаты получились статистически различными — XGBoost победил. Время работы XGBoost — незначительное, а у gcForestCS — минут по 20 каждая кросс-валидация на 5 фолдах. С другой стороны, авторы тестировали алгоритм на разных датасетах, и параметры для этого датасета подогнали под свою предобработку фичей.

Код можно посмотреть тут.

Реализации

Официальный код от авторов статьи: https://github.com/kingfengji/gcForest
Официальная улучшенная модификация, работает быстрее, но нет документации: http://lamda.nju.edu.cn/code_gcForestCS.ashx
Реализация попроще: https://github.com/pylablanche/gcForest

PcLasso: the lasso meets principal components regression

J. Kenneth Tay, Jerome Friedman, Robert Tibshirani (Stanford University)
Статья
Презентация
Пример использования

В начале 2019 года J. Kenneth Tay, Jerome Friedman и Robert Tibshirani из Stanford University предложили новый метод обучения с учителем, особенно подходящий для разреженных данных.

Авторы статьи решали задачу анализа данных исследования экспрессии генов, которые описаны в работе Zeng & Breesy (2016). Таргет — мутационный статус гена р53, который регулирует экспрессию генов в ответ на различные сигналы клеточного стресса. Целью исследования является выявление предикторов, которые коррелируют с мутационным статусом р53. Данные состоят из 50 строк, 17 из которых классифицированы как нормальные и оставшиеся 33 — несут мутации в гене р53. В соответствии с анализом в Subramanian et al. (2005) 308 наборов генов, которые имеют размер между 15 и 500, включены в этот анализ. Эти генные наборы содержат в общей сложности 4301 генов и доступны в пакете R «grpregOverlap». При расширении данных для обработки перекрывающихся групп выходит 13 237 столбцов. Авторы статьи применили метод «pcLasso», который помог улучшить результаты модели.

На картинке мы наблюдаем увеличение AUC при использовании «pcLasso»

Суть метода

Метод объединяет l_1 -регуляризацию с l_2 , которая сужает вектор коэффициентов к основным компонентам матрицы признаков. Они назвали предложенный метод «основные компоненты лассо» («pcLasso» доступный на R). Метод может быть особенно мощным, если переменные предварительно объединить в группы (пользователь выбирает сам, что и как группировать). В этом случае, pcLasso сжимает каждую группу и получает решение в направлении главных компонент этой группы. В процессе решения также выполняется выбор значимых групп среди имеющихся.

Мы представляем диагональную матрицу сингулярного разложения центрированной матрицы признаков следующим образом:

Наше сингулярное разложение центрированной матрицы X (SVD) представим как X=UDV^T , где — диагональная матрица, состоящая из сингулярных значений. В таком виде l_2 -регуляризацию можно представить:
$\beta^T VZV^T \beta$ где — диагональная матрица, содержащая функцию квадратов сингулярных значений: $Z_{11}=f_1 (d_1^2,d_2^2,…,d_m^2 ),…,Z_{22}=f_2 (d_1^2,d_2^2,…,d_m^2 )$ .

В общем случае, в l_2 -регуляризации $Z_{jj}=1$ для всех , что соответствует $\beta^T \beta$ . Они же предлагают минимизировать следующий функционал:

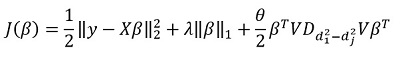
Здесь — матрица разностей диагональных элементов d_1^2-d_1^2,d_1^2-d_2^2,…,d_1^2-d_m^2 . Другими словами, мы контролируем вектор $\beta$ так же и при помощи гиперпараметра $\theta$ .
Преобразуя данное выражение, получим решение:

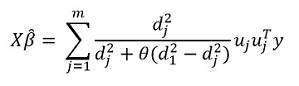
Но основная «фишка» метода, конечно, в возможности группировать данные, и на основании этих группировок выделять главные компоненты группы. Тогда перепишем наше решение в виде:

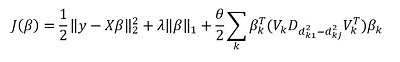
Здесь $\beta_k$ — подвектор вектора $\beta$ соответствующий группе k, $d_k=(d_{k1},…,d_{kmk})$ — сингулярные значения X_k , расположенные в порядке убывания, а $D_{d_{k1}^2-d_{kj}^2}$ — диагональная матрица $d_{k1}^2-d_{kj}^2, j=1,2,…,m_k$

Некоторые замечания по решению целевого функционала:

Целевая функция выпуклая, а негладкая составляющая отделима. Следовательно ее можно эффективно оптимизировать при помощи градиентного спуска.
Подход состоит в том, чтобы зафиксировать несколько значений $\theta$ (включая ноль, соответственно получая стандартную -регуляризацию), а затем оптимизировать: подбирая $\lambda$ . Соответственно, параметры $\theta$ и $\lambda$ подбираются на кросс-валидации.
Параметр $\theta$ трудно интерпретировать. В программном обеспечении (пакет «pcLasso»), пользователь сам задает значение этого параметра, которое принадлежит интервалу [0,1], где 1 соответствует $\theta$ = 0 (лассо).

На практике, варьируя значения $\theta$ = 0,25, 0,5, 0,75, 0,9, 0,95 и 1, можно охватить большой спектр моделей.

Сам алгоритм выглядит следующим образом

Данный алгоритм уже написан на R, при желании уже можно им пользоваться. Библиотека называется «pcLassо».

A Swiss Army Infinitesimal Jackknife

Ryan Giordano (UC Berkeley); William Stephenson (MIT); Runjing Liu (UC Berkeley);
Michael Jordan (UC Berkeley); Tamara Broderick (MIT)
Статья
Код

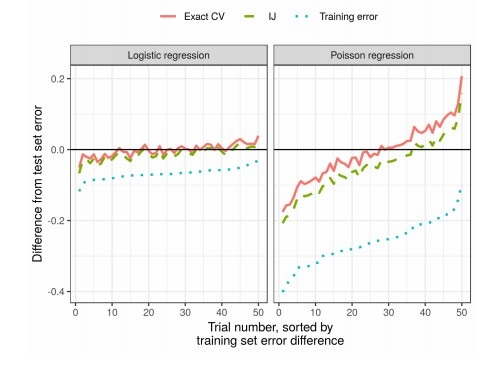
Качество алгоритмов машинного обучения часто оценивается путем многократной перекрестной проверки (сross-validation или bootstrap). Эти методы являются мощными, но медленными на больших наборах данных.

В данной работе коллеги используют линейную аппроксимацию весов, производя результаты, которые быстрее работают. Это линейное приближение известно в статистической литературе как «infinitesimal jackknife». Оно в основном используется в качестве теоретического инструмента для доказательства асимптотических результатов. Результаты статьи применимы вне зависимости от того, являются ли веса и данные стохастическими или детерминированными. Как следствие, это приближение последовательно оценивает истинную перекрестную проверку для любого фиксированного k.

Вручение Paper Award автору статьи

Суть метода

Рассмотрим задачу оценки неизвестного параметра $\theta \in \Omega_{\theta} \subset R^{D}$ , где $\Omega_{\theta}$ — компакт, а размер нашего датасета — . Наш анализ будет проводиться на фиксированном наборе данных. Определим нашу оценку $\theta \in \Omega_{\theta}$ следующим образом:

Для каждого , зададим ( $\theta$ ) — функция от $\Omega_{\theta} \subset R^{D}$
$\omega_n$ — вещественное число, а $\omega$ — вектор, состоящий из $\omega_n$

Тогда $\hat{\theta}$ можно представить как:

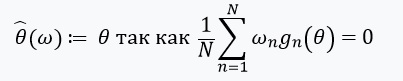
Решая данную задачу оптимизации градиентным методом, мы полагаем, что функции дифференцируемы и мы можем вычислить Гессиан. Основная проблема, которую мы решаем, — это вычислительные затраты, связанные с оценкой $\hat{\theta} ̂(\omega)$ для всех $\omega∈W$ . Основной вклад авторов статьи состоит в расчете оценки $\hat{\theta}_1=\hat{\theta}_1 (1_{\omega})$ , где $1_\omega=(1,1,…,1)$ . Другими словами, наша оптимизация будет зависеть только от производных $g_n (\theta)$ , которые, мы предполагаем, существуют, и являются Гессианом:

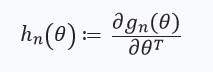
Далее зададим уравнение с фиксированной точкой и его производную: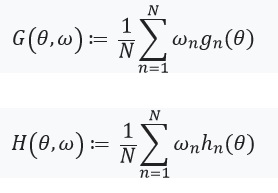

Здесь стоит обратить внимание, что $G(\theta ̂(\omega),w)=0$ , так как $\hat{\theta} (\omega)$ — решение для $\frac{ 1 }{ N } \sum_{n=1}^{N} \omega_n g_n (\theta)=0$ . Так же определим: $H_1=H(\hat{\theta}_1,1_\omega)$ , и матрицу весов как: $\Delta\omega= \omega-1_\omega \in R^{n}$ . В том случае, когда H_1 имеет обратную матрицу, мы можем использовать теорему о неявной функции и «chain rule» :

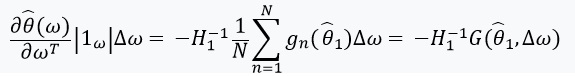
Эта производная позволяет нам сформировать линейную аппроксимацию $\hat{\theta} ̂(\omega)$ через $\hat{\theta}_1$ , которая выглядит следующим образом:

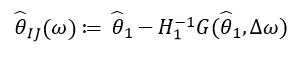
Так как $\hat{\theta}_{IJ}$ зависит только от $\hat{\theta}_1$ и $\Delta \omega$ , а не от решений при любых других значений $\omega$ , соответственно нет необходимости пересчитывать заново и находить новые значения ω. Вместо этого, нужно решить СЛУ (систему линейных уравнений).

Результаты

На практике это существенно сокращает время по сравнению с кросс-валидацией: