Deep Learning в вычислении оптического потока06.05.2019 14:17

С появлением множества различных архитектур нейронных сетей, многие классические Computer Vision методы ушли в прошлое. Все реже люди используют SIFT и HOG для object detection, а MBH для action recognition, а если и используют, то скорее как handcrafted-признаки для соответствующих сеток. Сегодня мы рассмотрим одну из классических CV-задач, в которой первенство по-прежнему остается за классическими методами, а DL-архитектуры томно дышат им в затылок.

Optical flow estimation

Задача вычисления оптического потока между двумя изображениями (обычно, между соседними кадрами видео) заключается в построении векторного поля $O$ такого же размера, причем $O(i, j)$ будет соответствовать вектору видимого смещения пикселя $(i, j)$ с первого кадра до второго. Построив такое векторное поле между всеми соседними кадрами видео, мы получим полную картину того, как передвигались те или иные объекты на нем. Иными словами, это задача трекинга всех пикселей на видео. Применяется оптический поток чрезвычайно широко — в задачах action recognition, например, такое векторное поле позволяет сконцентрироваться на движениях, происходящих на видео и уйти от его контекста [7]. Еще более распространенные приложения — визуальная одометрия, компрессия видео, его постобработка (например, добавление slow motion эффекта) и многое другое.

Тут есть место некоторым неоднозначностям — что именно считать видимым смещением с точки зрения математики? Обычно, предполагают что значения пикселей переходят из одного кадра в следующий без изменений, иными словами:

$I(i, j, t) = I(i+u_i, j+u_j, t+1),$

где $I(i, j, t)$ — интенсивность пикселя по координатам $(i, j)$ , тогда оптический поток $(u_i, u_j)$ показывает куда сместился этот пиксель в следующий момент времени (т.е. на следующем кадре).

В картинке это выглядит так:

Визуализировать векторное поле непосредственно векторами наглядно, но не всегда удобно, поэтому второй распространенный способ — визуализация цветом:

Каждый цвет на этой картинке кодирует определенный вектор. Для простоты, вектора длиннее 20-ти обрезаются, а сам вектор по цвету можно восстановить из следующей картинки:

Больше оптического котенка!

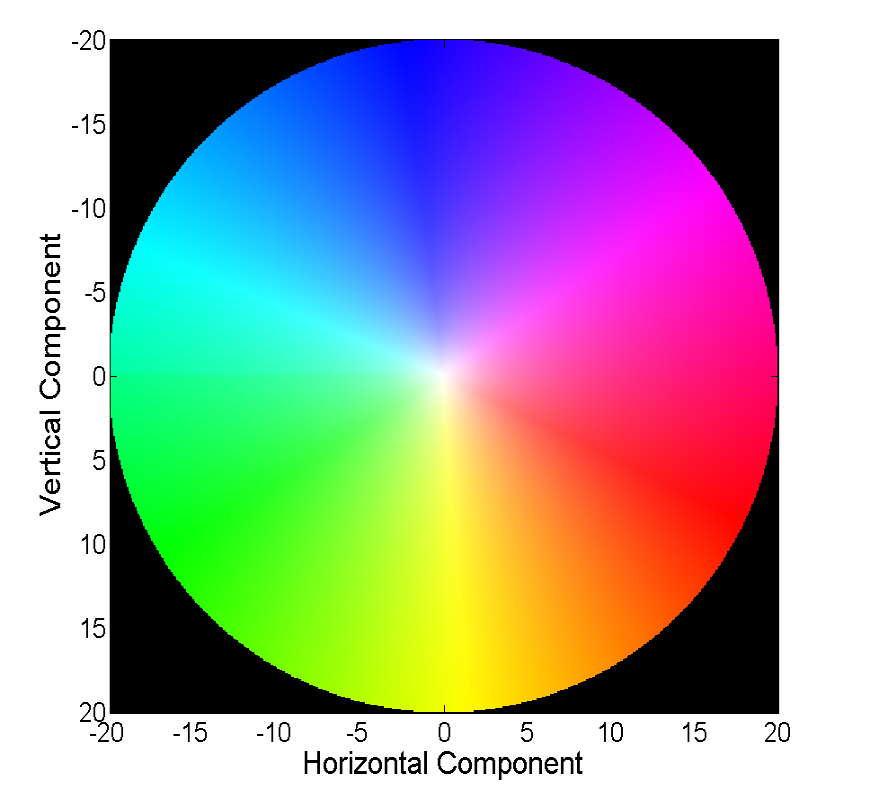
Классические методы добились довольно неплохой точности, за которую порой приходится платить скоростью работы. Мы же рассмотрим прогресс, которого достигли нейронные сети в решении этой задачи за последние 4 года.

Данные и метрики

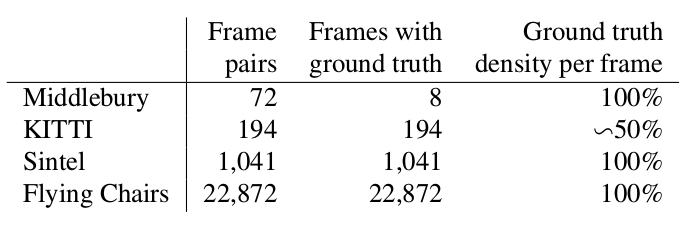
Два слова о том, какие датасеты были доступны и популярны на момент начала нашего рассказа (т.е. 2015 год), а также каким способом измеряют качество получившегося алгоритма.Middlebury
Крохотный датасет из 8 пар изображений с небольшими смещениями, который, тем не менее, иногда используется при валидации алгоритмов вычисления оптического потока и сейчас.

KITTI
Это датасет, размеченный под приложения для self-driving автомобилей и собранный с помощью технологии LIDAR. Он широко используется для валидации алгоритмов вычисления оптического потока и содержит множество довольно сложных случаев с резкими переходами между кадрами.

Sintel
Еще один очень распространенный бенчмарк, созданный на основе открытого и нарисованного в Blender мультика Sintel в двух версиях, которые обозначаются как clean и final. Второй намного сложнее, т.к. содержит множество атмосферных эффектов, шумов, блюра и прочих неприятностей для алгоритмов вычисления оптического потока.

[embedded content]

EPE
Стандартная функция ошибки для задачи вычисления оптического потока — это End Point Error или EPE. Это просто Евклидово расстояние между рассчитанным алгоритмом и истинным оптическим потоком, усредненный по всем пикселям.

Flownet (2015)

Взявшись за построение архитектуры нейронной сети для задачи вычисления оптического потока в далеком 2015, авторы (из Мюнхенского и Фрайбургского университетов) столкнулись с двумя проблемами: под данную задачу не было большого размеченного датасета, а его разметка вручную составляла бы определенные сложности (попробуй разметить куда двинулся каждый пиксель изображения на следующем кадре), во-первых. Данная задача довольно сильно отличалась от всех задач, которые решались при помощи CNN-архитектур до этого, во-вторых. По-сути, это задача попиксельной регрессии, что делает ее схожей с задачей сегментации (попиксельная классификация), но вместо одного изображения у нас на входе два, причем интуитивно, признаки должны каким-то образом показывать разницу между этими двумя изображениями. В качестве первой итерации было решено в качестве входа просто стакнуть два RGB-кадра (получив, по-сути, 6-канальное изображение), между которыми мы хотим подсчитать оптический поток, а в качестве архитектуры взять U-net с рядом изменений. Такую сеть назвали FlowNetS (S значит Simple):

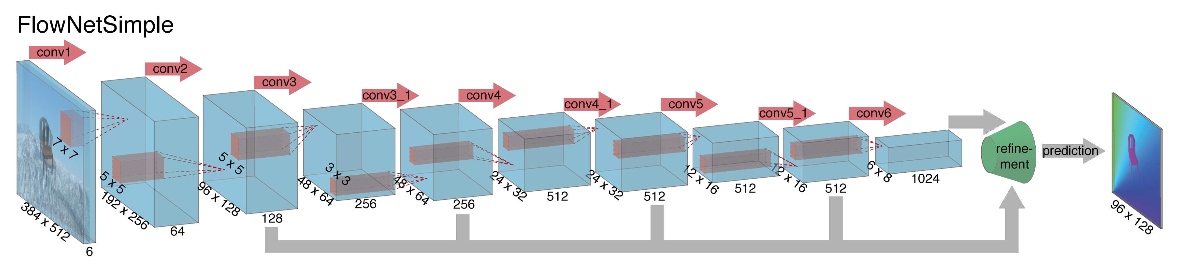
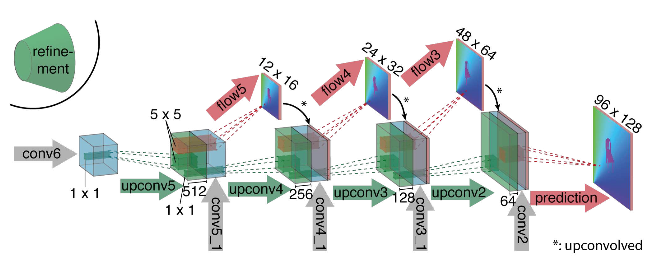
Как видно из схемы, энкодер ничем не примечателен, декодер же отличается от классических вариантов несколькими вещами:

Предсказание оптического потока происходит не только с последнего уровня, но также и со всех остальных. Чтобы получить Ground Truth для i-го уровня декодера, исходный таргет (т.е. оптический поток) просто уменьшается (почти так же, как и изображение) до нужного разрешения, а сам предикт, получившийся на i-м уровне докидывается дальше, т. е. конкатенируется с выходящей из этого уровня картой признаков. Общая функция потерь при обучении будет являться взвешенной суммой лоссов со всех уровней декодера, сам вес будет при этом тем больше, чем ближе уровень к выходу сети. Авторы не дают объяснения почему так делается, но скорее всего причиной служит тот факт, что резкие движения лучше детектировать на ранних уровнях, тогда на оптическом потоке меньшего разрешения вектора не будут такими большими.
На схеме видно, что входное разрешение изображений — 384×512, а у выхода в четыре раза меньше. Авторы заметили, что если увеличить такой выход до 384×512 простой билинейной интерполяцией, это даст такое же качество, как если прикрепить еще два уровня декодера. Также можно использовать вариационный подход [2], что докидывает еще качества (+v в таблице с качеством).
Как и в U-net, карты признаков с энкодера прокидываются в декодер и конкатенируются как показано на схеме.

Чтобы понять, как авторы попробовали улучшить свой бейзлайн, нужно знать, что такое корреляция между изображениями и почему она может быть полезна при подсчете оптического потока. Итак, имея два изображения и зная, что второе является следующим кадром в видео относительно первого, мы можем попытаться сопоставить область вокруг точки на первом кадре (для которой хотим найти сдвиг до второго кадра) с областями такого же размера на втором изображении. При этом предполагая, что за единицу времени сдвиг не мог быть слишком большим, сопоставление можно считать лишь в некоторой окрестности исходной точки. Для этого используется кросс-корреляция. Поясним на примере.

Возьмем два соседних кадра видео, мы хотим определить куда сместилась определенная точка с первого кадра до второго. Предположим, что некоторая область вокруг этой точки сдвинулась точно также. Действительно, соседние пиксели на видео обычно смещаются вместе, т.к. скорее всего, визуально, являются частью одного объекта. Это предположение активно используется, например, в дифференциальных подходах, о чем можно подробней прочитать в [5], [6].

fig, ax = plt.subplots(1, 2, figsize=(20, 10))
ax[0].imshow(frame1)
ax[1].imshow(frame2);

Попробуем взять точку в центре лапки котенка и найти ее же на втором кадре. Возьмем некоторую область вокруг нее.

patch1 = frame1[90:190, 140:250]
plt.imshow(patch1);

Рассчитаем корреляцию между этой областью (в англоязычной литературе часто пишут template или patch с первого изображения) и вторым изображением. Шаблон будет просто «гулять» по второму изображению и рассчитывать следующую величину между собой и кусочками такого же размера на втором изображении:

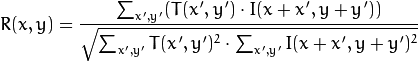
Чем больше будет значение этой величины, тем больше шаблон похож на соответствующий кусок на втором изображении. С помощью OpenCV это можно сделать так:

corr = cv2.matchTemplate(frame2, patch1, cv2.TM_CCORR_NORMED)
plt.imshow(corr, cmap='gray');

Подробнее можно почитать в [7].

Результат выглядит следующим образом:

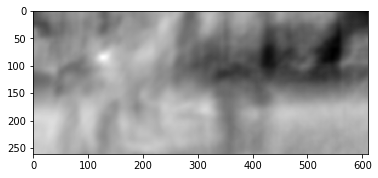
Мы видим явный пик, обозначенный белым цветом. Найдем его на втором кадре:

min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(corr)
h, w, _ = patch1.shape
top_left = max_loc
bottom_right = (top_left[0] + w, top_left[1] + h)
frame2_copy = frame2.copy()
cv2.rectangle(frame2_copy, top_left, bottom_right, 255, 2)
plt.imshow(frame2_copy);

Видим, что лапка нашлась правильно, по этим данным мы можем понять в какую сторону она сдвинулась с первого кадра до второго и рассчитать соответствующий этому оптический поток. Кроме того, оказывается, такая операция довольно устойчива к фотометрическим искажениям, т.е. если яркость на втором кадре резко возрастает, пик кросс-корреляции между изображениями останется на своем месте.

Учитывая все вышесказанное, авторы решили ввести в свою архитектуру так называемый correlation layer, но считать корреляцию было решено не по входным изображениям, а по картам признаков после нескольких слоев энкодера. Такой слой, по понятным причинам, не имеет обучающихся параметров, хотя и похож по своей сути на свертку, но вместо фильтров здесь используются не веса, а некоторая область второго изображения:

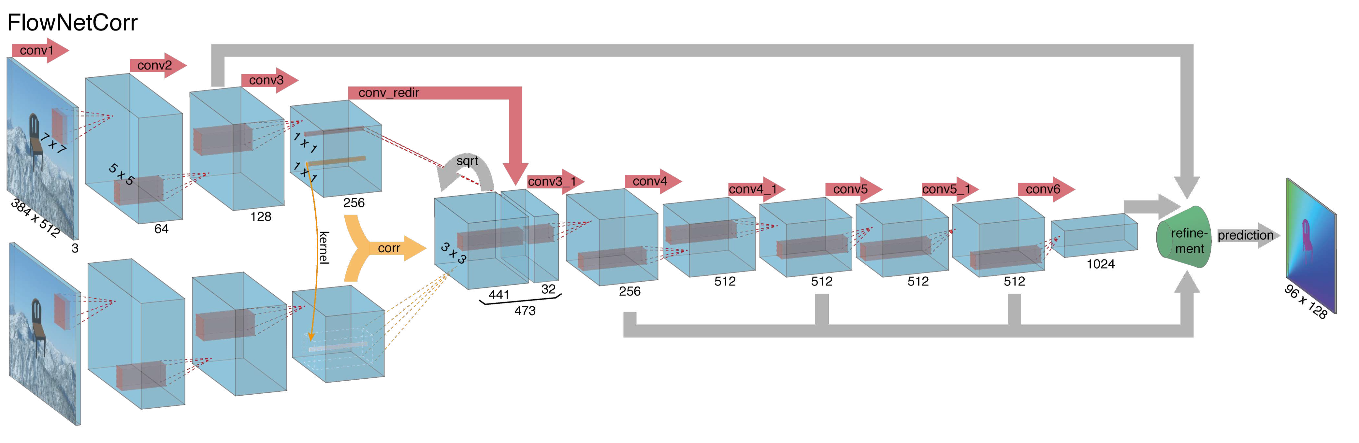
Как ни странно, такой трюк не дал значительного улучшения качества у авторов данной статьи, однако, был более успешно применен в дальнейших работах, а в [9] авторы смогли показать, что немного изменив параметры обучения можно заставить FlowNetC работать намного лучше.

Проблему с отсутствием датасета авторы решили довольно изящным образом: наскрапили 964 изображений с Flickr по темам: «city», «landscape», «mountain» в разрешении 1024 × 768 и использовали их кропы 512 × 384 в качестве фона, на который затем накинули несколько стульев из открытого сета отрендеренных 3D-моделек. Затем на стулья и фон независимо применяли различные аффинные преобразования, которые использовались для генерации второго изображения в паре и оптического потока между ними. Результат выглядит следующим образом:

Интересным результатом стало то, что использование такого синтетического датасета позволило добиться относительно хорошего качества и для данных из другого домена. Файн-тюн на соответствующих данных, разумеется, докидывал еще качества (+ft в таблице ниже):

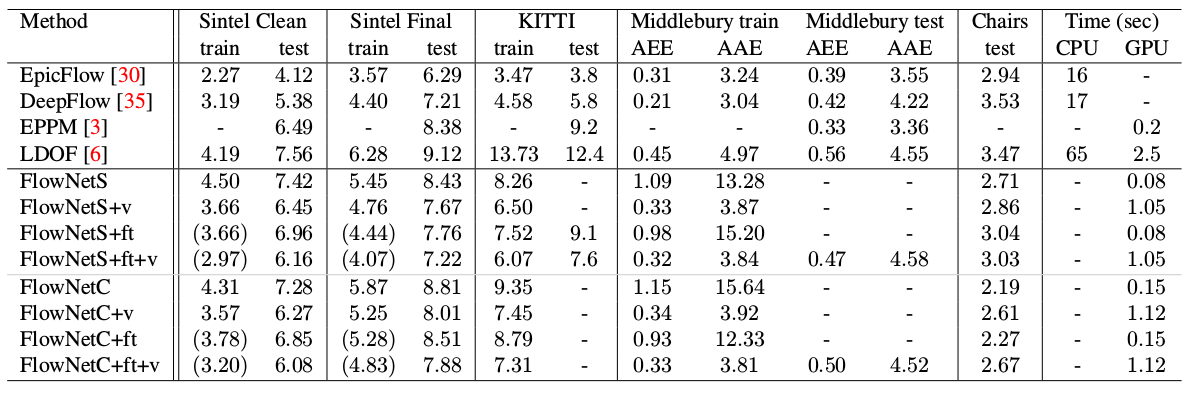
Результат на реальных видео можно посмотреть здесь:

[embedded content]

SpyNet (2016)

Во многих последующих статьях, авторы пытались улучшить качество путем решения проблемы плохого распознавания резких движений. Интуитивно, движение не будет схвачено сетью, если его вектор значительно выходит за receptive field активации. Решить эту проблему предлагается засчет трех вещей: сверток большего размера, пирамид и «оборачивания» (warping) одного изображения из пары в оптический поток. Обо всем по-порядку.

Итак, если у нас есть пара изображений, на которых объект резко сместился (10+ пикселей), то мы можем просто уменьшить изображение (в 6 или более раз). Абсолютное значение смещения значительно уменьшится, и сеть с большей вероятностью сможет его «поймать», особенно, если его свертки будут больше, чем само смещение (в данном случае используются свертки 7×7).

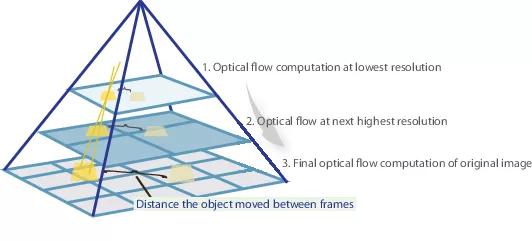
Однако, при уменьшении изображения, мы потеряли много важных деталей, поэтому следует перейти на следующий уровень пирамиды, в котором размер изображения уже больше, при этом как-то учесть информацию, которую мы получили до этого, когда рассчитывали оптический поток на меньшем размере. Это делается при помощи warping operator, который пересчитывает первое изображение согласно имеющемуся приближению оптического потока (полученного на предыдущем уровне). Улучшение в данном случае состоит в том, что первое изображение, которое «подвинули» согласно приближению оптического потока будет ближе ко второму, чем исходное, т. е. мы снова уменьшаем абсолютное значение оптического потока, которое нам надо предсказать (напомню, небольшие по значению движения детектируются намного лучше, т. к. полностью входят в одну свертку). С точки зрения математики, имея растровое изображение I и приближение оптического потока V, warping operator можно описать так:

$w(I, V) = I_w,\;\; I_w(x) = I(x+V(x)),$

где $x=(i, j)$ , т.е. определенная точка на изображении, $I$ — само изображение, $V$ — оптический поток, $I_w$ — результирующее изображение, «обернутое» в оптический поток.

Как же применить это все в CNN-архитектуре? Зафиксируем количество уровней пирамиды $k$ и множитель, на который уменьшается каждое последующее изображение на уровне, начиная с последнего $n$ . Обозначим за $d(*)$ и $u(*)$ функции уменьшения (downsampling) и увеличения (upsampling) изображения или оптического потока на этот множитель.

Заведем себе также набор CNN-ок { $G_0...G_k$ }, по одной на каждый уровень пирамиды. Тогда $G_i$ -я сеть будет принимать на вход пару изображений с $i$ -го уровня пирамиды и оптический поток, подсчитанный на $G_{i-1}$ -м уровне ( $G_0$ будет просто принимать тензор из нулей вместо этого). При этом одно из изображений мы будем отправлять в warping layer, чтобы уменьшить разницу между ними, а предсказывать будем не сам оптический поток на этом уровне, а значение, которое нужно прибавить к увеличенному (upsampled) оптическому потоку с предыдущего уровня, чтобы получить оптический поток на этом уровне. В формуле это выглядит примерно так:

$v_k=G_k(I_k^1, w(I_k^2, u(V_{k-1})), V_{k-1})$

Чтобы получить сам оптический поток, мы просто сложим предикт сети и увеличенный поток с предыдущего уровня:

$V_k=u(V_{k-1})+v_k.$

Для получения Ground Truth для сети на этом уровне нам нужно проделать обратную операцию — вычесть из таргета (уменьшенного до нужного уровня) предикт с предыдущего уровня пирамиды. Схематично, это выглядит так:

Преимущество такого подхода в том, что каждый уровень мы можем обучать независимо. Авторы начинали обучение с 0-го уровня, каждая последующая сеть при этом инициализировалась параметрами предыдущей. Так как каждая сеть $G_i$ решает задачу намного более простую, чем полное вычисление оптического потока на большом изображении, то и параметров можно сделать намного меньше. Настолько меньше, что теперь весь ансамбль целиком может поместиться на мобильные устройства:

Сам ансамбль выглядит следующим образом (пример пирамиды из 3х уровней):

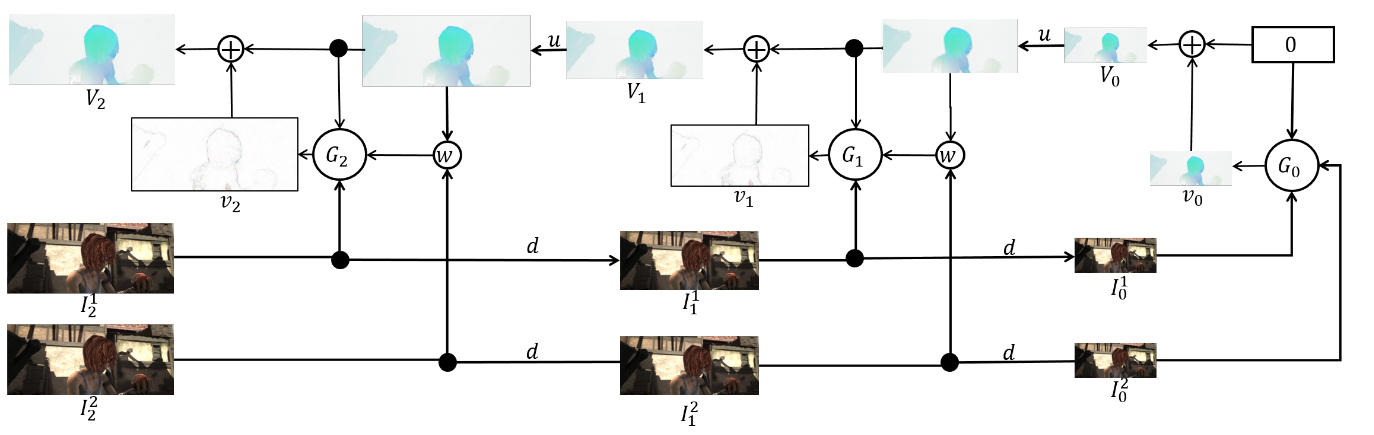
Осталось поговорить непосредственно об архитектуре $G_i$ -ой сети и подвести итоги. Каждая сеть $G_i$ состоит из 5-ти сверточных слоев, каждая из которых заканчивается ReLU-активацией, кроме последней (которая предсказывает оптический поток). Количество фильтров на каждом слое равно соответственно { $32, 64, 32, 16, 2$ }. Входы нейронной сети (изображение, второе изображение «обернутое» в оптический поток и сам оптический поток) просто конкатенируются по размерности каналов, так что входной тензор их имеет 8. Результаты впечатляют:

PWC-Net (2018)

Вдохновившись успехами немецких коллег, ребята из NVIDIA решили применить свой опыт (и видеокарточки), чтобы еще сильнее улучшить результат. В основу их работы во-многом легли идеи из предыдущей модели (SpyNet), поэтому PWC-Net тоже будет иметь дело с пирамидами, но с пирамидами сверток, а не исходных изображений, однако, опять же — обо всем по-порядку.

Использование сырых значений интенсивности пикселей для подсчета оптического потока не всегда разумно, т.к. резкое изменение яркости/контрастности сломает наше предположение о том, что пиксели переходят из одного кадра в следующий без изменений и алгоритм будет не устойчив к таким изменениям. В классических алгоритмах подсчета оптического потока применяются различные преобразования, которые смягчают эту ситуацию, в данном же случае авторы решили предоставить модели возможность самой выучить такие преобразования. Поэтому вместо пирамиды изображений в PWC-Net используются пирамиды сверток (отсюда первая буква в Pwc-Net), т.е. просто карты признаков с разных слоев CNN, которую здесь называют feature pyramid extractor.

Дальше все почти как в SpyNet, только перед тем, как подать в CNN, которая здесь называется optical flow estimator, все необходимое, а именно:

изображение (в данном случае — карту признаков из feature pyramid extractor),
рассчитанный на предыдущем уровне апсемпленный оптический поток,
второе изображение, «обернутое» (помните warping layer, отсюда вторая буква в pWc-Net) в этот оптический поток,

между «обернутым» вторым кадром и обычным первым (снова напоминаю, что вместо сырых изображений здесь используются карты признаков с feature pyramid extractor) считают то, что здесь называют cost volume (отсюда третья буква в pwC-Net) и что является по-сути уже рассмотренной ранее корреляцией между двумя изображениями.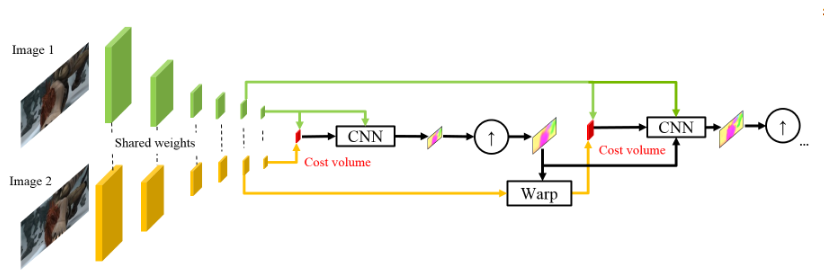

Последний штрих — это context network, который добавляется сразу после optical flow estimator и играет роль обучаемого пост-процессинга для подсчитанного оптического потока. Подробности архитектур можно посмотреть под спойлером либо в исходной статье.

Интимные подробности

Результаты впечатляют еще больше:

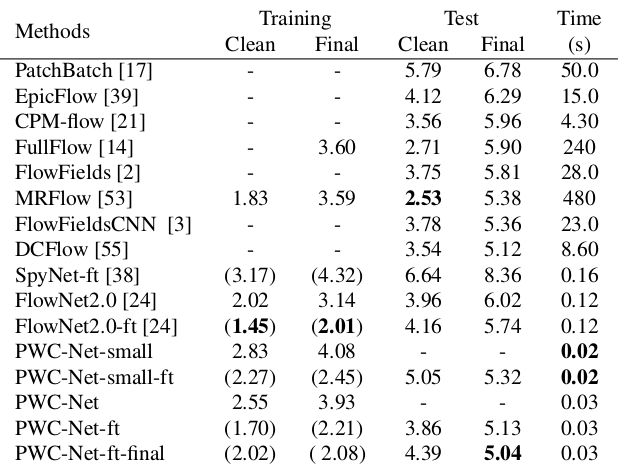
В сравнении с прочими CNN-методами вычисления оптического потока, PWC-Net достигает баланса между качеством и количеством параметров:

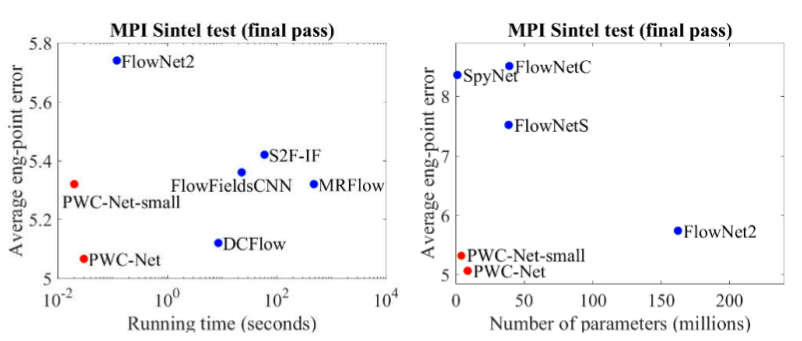
Также есть отличное выступление самих авторов, в котором они рассказывают о самой модели и их экспериментах:

[embedded content]

Заключение

Эволюция архитектур, решающих задачу подсчета оптического потока — замечательный пример того, как прогресс в CNN-архитектурах и комбинирование их с классическими методами дает все лучший и лучший результат. И хотя классические CV-методы все еще выигрывают в качестве, последние результаты дают надежду, что это поправимо…

Источники и ссылки

1. FlowNet: Learning Optical Flow with Convolutional Networks: статья, код.
2. Large displacement optical flow: descriptor matching in variational motion estimation: статья.
3. Optical Flow Estimation using a Spatial Pyramid Network: статья, код.
4. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume: статья, код.
5. То, что вы хотели знать про оптический поток, но стеснялись спросить: статья.
6. Вычисление оптического потока методом Лукаса-Канаде. Теория: статья.
7. Template matching with OpenCVP: дока.
8. Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset: статья.
9. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks: статья, код.