Custom floating point format on FPGA
Всем привет!
В данной статье речь пойдет о числах в формате с плавающей точкой и в частности о реализации специализированного формата FP23 на программируемых логических интегральных схемах (ПЛИС). В рамках конкретного проекта у меня родилась мысль реализовать оптимальный для определенных нужд формат данных с плавающей точкой. В итоге эта мысль переросла в реальный проект, который впоследствии нашел применение в некоторых интересных задачах цифровой обработки сигналов. В статье рассмотрены основные сложности при реализации формата данных floating point на ПЛИС Xilinx, рассмотрены базовые математические операции в формате FP23. Также в конце статьи вы можете найти исходный код проекта, которой можно свободно использовать в своих задачах или на его основе реализовать похожие форматы данных.
Формат данных
Числа с плавающей точкой активно используются в современных сигнальных процессорах, видеокартах и даже в ПЛИС. В соответствии со стандартом IEEE 754, они представляются в виде совокупности экспоненты (показателя степени), мантиссы и знака. Числа в стандарте IEEE 754 имеют 32 бита (float). Для однозначности записи числа во float записываются в нормальной форме или приводятся к нормализованному виду после математических операций и преобразований над числами. Диапазон возможных значений зависит от количества бит мантиссы и экспоненты. Для float характерна фиксированная относительная точность и переменная абсолютная точность. Основные преимущества и недостатки чисел в формате float:
- + Обеспечивается очень широкий диапазон возможных значений;
- + Достигается высокая точность вычислений;
- — Округление очень больших чисел до возможных из сетки значений;
- — Потеря точности при суммировании чисел, отличных друг от друга во много раз;
- — Сложность реализации и применения на ПЛИС.
Для современных микросхем ПЛИС реализация чисел в формате с плавающей точкой не составляет большого труда. Для ведущих производителей — Xilinx и Altera существуют готовые SOFT IP-ядра, реализующие float по стандарту. Для Altera в последних семействах представлены HARD IP-ядра, реализующие формат IEEE 754 на DSP-блоках.
Цифровая часть
Основная элементная база для выполнения математических операций и задач цифровой обработки сигналов — передовые семейства ПЛИС. Работа проводится на ПЛИС фирмы Xilinx, которые содержат блоки векторов конфигурируемых ячеек. В первую очередь это универсальные блоки цифровой обработки и математики — DSP48E1 (для ПЛИС серии Virtex-6 и 7 семейства) и DSP48E2 (для ПЛИС семейства UltraScale). Эти блоки позволяют выполнять функции сложения и вычитания чисел, сдвига и переноса, быстродействующего умножения, перемножения с накоплением (MACC), поиска контрольной суммы и т.д. На ячейках DSP48 в современных ПЛИС выполняется множество задач — разработка СIC и FIR фильтров, скоростное вычисление FFT/IFFT, реализация цифровых синтезаторов частоты (DDS и CORDIC), создание различных форматов представления данных и набора операций для них.
Вторым базовым компонентом ПЛИС является блочная память. Для ПЛИС Xilinx это ячейки RAMB36E1 (или RAMB18E1). Это элементы двухпортовой памяти, реализованные внутри кристаллов в виде столбцов идентичных блоков. Количество столбцов встроенной памяти зависит от объема кристалла. Максимальный объем блока памяти составляет 36Кбит, при этом он может быть сконфигурирован как два независимых блока по 18Кбит каждый. Память может быть использована с шириной данных от 1 до 72 разрядов. При отсутствии свободных ресурсов блочной памяти ПЛИС, можно задействовать распределенную память в специальных ячейках SLICEM. Для ПЛИС Ultrascale объем такой памяти до 512×1, с возможностью реконфигурации глубины и разрядности шины.
Постановка задачи
С учетом перечисленных особенностей для реализации аналоговой и цифровой части, задача формируется следующим образом. Пусть разрядность данных, поступающих в кристалл ПЛИС с микросхем АЦП равна 16 бит. В качестве ПЛИС выбрана самая маленькая микросхема Kintex-7. Задача состоит в переводе 16-разрядного знакового целого числа FIX16 в специализированный формат с плавающей точкой FP23 и обратно, обеспечивая при этом максимальную скорость обработки внутри ПЛИС при минимальных затратах ресурсов кристалла. Кроме того, необходимо обозначить и реализовать набор базовых математических операций — сложение, вычитание и умножение.
Реализация формата FP
FP23 — это особый формат представления чисел с плавающей точкой. В отличие от стандарта IEEE 754, длина слова в формате FP23 не 32 бита, а всего 23 бита. Следующая формула в упрощенном виде отражает представление числа «A» в формате FP: 
Мантисса (mantissa) в формате FP23 — это 17-битное положительное число. Она всегда отображается в нормализованном виде в результате всех преобразований, т.е. самый старший бит мантиссы всегда равен »1». Для экономии ресурсов кристалла и упрощения записи 17-й бит мантиссы никогда не отображается в упакованном результирующем 23-битном слове (см. рисунок). Поэтому при вычислении математических операций и переводе из одного формата в другой необходимо помнить, что мантисса нормализована, и к 16-разрядному ненулевому числу необходимо прибавить значение 216. Экспонента или показатель (exponent) в формате FP23 — это 6-битное положительное число, определяющее, на сколько умножается мантисса. Под знак (sign) выделен оставшийся один бит, причем нулевое значение бита соответствует положительным числам, а единичное значение определяет отрицательные числа. Таким образом, число A в формате FP23 описывается тремя битовыми полями: «экспонентой» (EXP (A)), «знаком»(SIGN (A)) и «мантиссой» (MAN (A)).
В таблице 1 приведены разрядность данных, диапазон возможных значений мантиссы и экспоненты и т.д.
Итак, первый этап при разработке формата данных с плавающей точкой на ПЛИС состоит в переводе знакового целого числа фиксированной разрядности в формат с плавающей точкой FP23, обеспечивая при этом максимальную скорость обработки внутри ПЛИС. Второй этап заключается в обратном преобразовании чисел из формата FP23 в формат с фиксированной точкой с возможностью масштабирования выходных данных под определенный коэффициент деления. И, наконец, на третьем этапе для полноценного использования всей мощи формата FP23 необходимо реализовать математические операции — сложение, вычитание и умножение.
Перед описанием модулей FP23 предстоит ответить на закономерный вопрос: «Почему разрядность данных в формате именно 23 бита?» Ответ складывается из нескольких составляющих. Во-первых, один бит используется для знака и 15 оставшихся битов для целой части, поэтому мантисса и знак занимают как минимум 16 битов. Для экспоненты с учетом смещения в формуле необходимо минимум 5 битов. Чем больше битов отводится под экспоненту, тем больше результат (расширяется диапазон возможных значений). Пусть экспонента имеет 6 разрядов, а мантисса представлена как 16-разрядное число, на знак отводится 1 разряд. Тогда для представления чисел в формате FP23 используется именно 23 бита. Если использовать скрытый бит мантиссы, который равен 1 при ненулевых значениях и равен 0 при нулевых значениях двоичного числа, то разрядность равна 24.
Кроме того, значение »23» выбрано не случайно, т.к. в дальнейшем для хранения вектора комплексных значений потребуется память ПЛИС. Пара значений без отображения скрытого бита имеет суммарную разрядность равную 46, со скрытым битом — 48, что по ширине данных укладывается ровно в три блока памяти RAMB18E1. Также для пары значений можно использовать дополнительные функции блока DSP48E1 ¬– быстрое сравнение двух чисел, проверка на четность и быстрое суммирование в режиме SIMD.
Преобразование FIX16-to-FP23
Для преобразования данных из целочисленного знакового типа FIX16 в формат FP23 необходимо использовать логику кристалла ПЛИС и встроенные перемножители DSP48E1. На рисунке зображена структурная схема преобразования данных в формат FP23.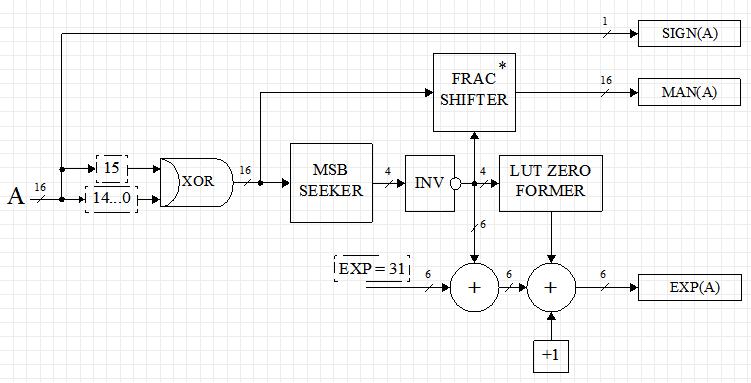
Максимальная разрядность множителей блоков DSP48E1 — 25 и 18 соответственно, где старший бит¬ — знаковый. Для перемножения чисел без учета знака в модуле DSP48E1 эффективная разрядность входных данных понижается на 1 бит. Блочную память RAMB18E1 преобразователь не использует.
Соответственно, чтобы найти знак числа, необходимо взять старший (знаковый) бит входных данных. Алгоритм поиска мантиссы MAN (A) на базе примитивов ПЛИС следующий:
- взять модуль входного числа (операция «исключающее ИЛИ»),
- произвести поиск старшего значащего бита (MSB SEEKER),
- по старшему значащему биту сформировать величину сдвига мантиссы,
- перемножить модуль числа и значение сдвига, получив нормализованную мантиссу (FRAC SHIFTER).
Для поиска экспоненты EXP (A) необходимо:
- взять модуль входного числа (операция «исключающее ИЛИ»),
- произвести поиск старшего значащего бита (MSB SEEKER),
- вычесть из числа »32» инвертированный индекс значащего бита,
- прибавить 1 к полученному результату с учетом логики поиска ненулевого входного значения (LUT ZERO FORMER).
Поскольку мантисса получается путем умножения модуля действительного числа на некоторую «маску», от которой зависит сдвиг входного числа без знака, то для ее поиска необходим блок DSP48E1. Процедура поиска и формирования мантиссы происходит в узле FRAC SHIFTER и отражена на рисунке.
Как видно, мантисса формируется в два этапа. На первой стадии с помощью логических ресурсов LUT из входного числа создается множитель 216-MSB. На второй стадии входные данные умножаются на величину сдвига в узле DSP48E1. На выходе умножителя образуется нормализованная мантисса. Согласно описанию, для умножения чисел без знака максимальная разрядность одного из множителей блока DSP48E1 равна 17, следовательно, мантисса и формируемый сдвиг не могут иметь большую разрядность. Это ограничение еще раз обуславливает тот факт, что мантисса чисел в формате FP23 имеет разрядность 17. Старший бит мантиссы для ненулевых чисел равен 1, зарезервирован и применяется в операции поиска результирующей мантиссы, но не отображается в выходном представлении числа для нормализованного вида. Этот бит можно вывести и использовать в общем представлении слова, тогда разрядность выходного слова равна 24 битам.
Для уменьшения объема занимаемых ресурсов кристалла, блок DSP48E1 можно исключить. Тогда узел поиска мантиссы преобразуется в быстрый сдвиговый регистр (Barrel shifter). Для некоторых кристаллов ПЛИС количество DSP48E1 невелико, и лишние траты ресурсов критичны, поэтому при использовании блоков FP23 есть возможность выбрать тот или иной вариант. Кроме того, для варианта с использованием быстрого сдвига суммарная задержка на полное выполнение операции преобразования уменьшается на один такт.
Узлы суммирования для поиска экспоненты сделаны в виде полных двоичных сумматоров, для реализации которых применяются логические компоненты MUXCY, XORCY и CARRY CHAIN, входящие в базовые ячейки SLICEL и SLICEM. Подробное описание можно найти в любой литературе, посвященной программируемой логике.
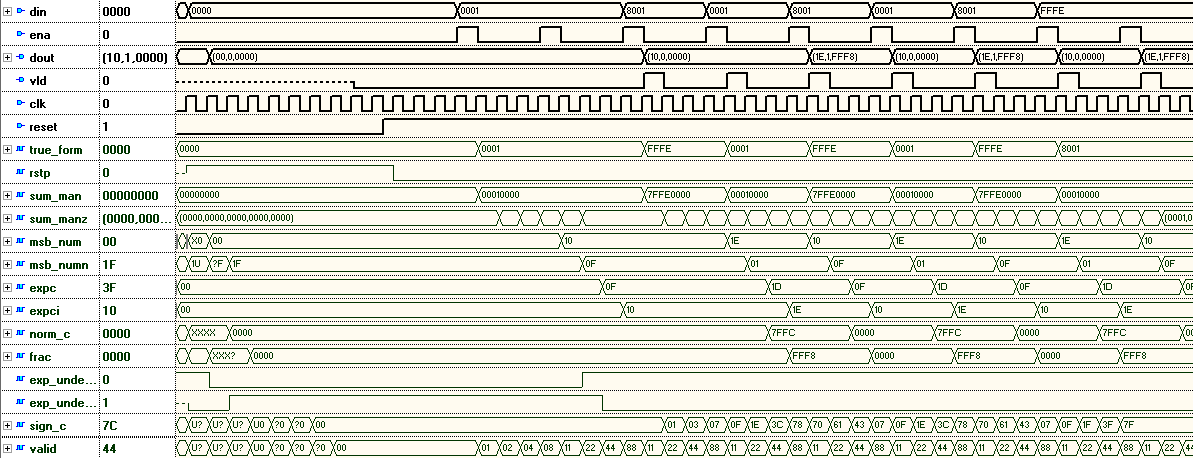
DIN — входные данные, 16 бит. DOUT — число в формате FP23, разбитое на три поля: {EXP, SIGN, MANT}.
Преобразование FP23-to-FIX16
Преобразование данных из формата FP23 в FIX16 производится в четыре этапа.
Алгоритм поиска двоичного знакового числа A состоит из нескольких последовательных действий:
- из экспоненты EXP (A) вычесть значение SCALE (масштабирование выходных данных),
- сформировать сдвиговую маску 2(EXP (A)-SCALE),
- к мантиссе прибавить скрытый бит IMPL (A) и умножить результат на величину сдвига,
- учесть знак числа SIGN (A) путём взятия операции «исключающее ИЛИ».
Как и для узла прямого преобразования в формат FP23, в этой схеме для экономии ресурсов ПЛИС блок DSP48E1 можно заменить быстрым сдвиговым регистром, выполненным на ячейках SLICEM.
Умножение
Умножение чисел в формате FP23 — одна из самых простых и логичных операций. Аппаратно алгоритм умножения реализован следующим образом (см. рис).
- умножение мантисс в узле DSP48E1,
- нормализация мантиссы (взятие в качестве мантиссы разрядов [32…17] или [31…16], в зависимости от значения старшего значащего бита),
- сложение экспонент,
- вычитание из суммы экспонент числа 16,
- если 33-й бит произведения мантисс равен »0», то из экспоненты результата вычитается еще 1,
- определение знака произведения с помощью операции «исключающее ИЛИ».

В схеме не отражена логика умножения на нулевое число, но алгоритмически она сводится к тому, что если экспонента любого входного числа равна нулю, то результат на выходе также равен нулю. На ПЛИС поиск нуля организован с помощью логических функций AND и OR на базовых блоках LUT.
Число 16 вычитается из суммы экспонент для учета скрытых битов в мантиссах входных чисел, которые дают прибавку к экспонентам. Сумматоры и вычитатели в узле умножения чисел в плавающей точке также реализованы по схеме двоичного полного сумматора.
Сложение и вычитание
Сложение и вычитание чисел в формате FP23 — самая затратная по ресурсам операция (см. рис). Сложение чисел в формате FP23 состоит из следующих фундаментальных стадий:
- приведение операндов к одной экспоненте (выравнивание),
- сложение мантисс,
- нормализация результата (подбор такой экспоненты, чтобы 16 бит мантиссы был равен »1»).
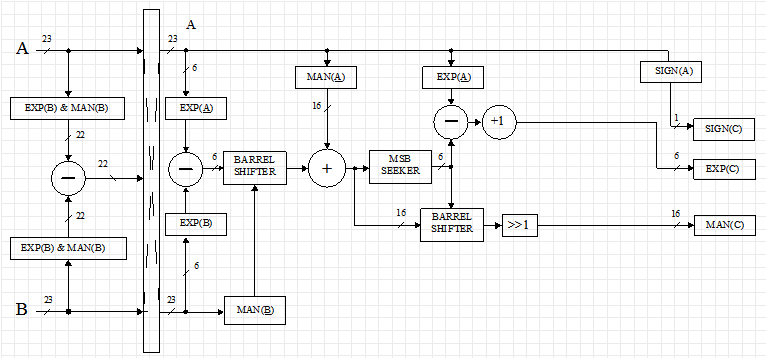
Аппаратно алгоритм сложения реализован следующим образом:
- операнды «A» и «B» сравниваются по модулю, если |А|<|B|, числа меняются местами,
- вычисляется разность экспонент операндов, а результат определяет, на сколько разрядов нужно сдвинуть мантиссу числа «B» вправо, чтобы привести числа к одной экспоненте,
- по разности экспонент формируется число, на которое умножается мантисса числа «В»,
- результат умножения складывается с мантиссой числа «A»,
- в полученном числе определяется номер старшего значащего бита MSB, формируется число ,
- нормализация мантиссы путем умножения суммы мантисс на число ,
- экспонента числа EXP© = EXP (A) — MSB + 1.
Вычитание реализовано аналогично сложению. Отличие только в том, что у вычитаемого операнда инвертируется знак SIGN (B). Блоки DSP48E1 также можно заменить на быстрый сдвиговый регистр.
Ресурсы
Результаты синтеза и задержка распространения на выполнение операции для каждого узла сведены в таблицу 2. Из таблицы видно, что самой простой и быстрой операцией является умножение двух чисел в формате FP23.
Объем занимаемых ресурсов после синтеза для всех узлов приведен в общем лог-файле. Пример результатов синтеза для умножителя fp23:
Top Level Output File Name : fp23_mult_m1.ngc
Primitive and Black Box Usage:
------------------------------
# BELS : 106
# GND : 15
# INV : 1
# LUT2 : 25
# LUT3 : 16
# LUT4 : 6
# LUT6 : 14
# MUXCY : 14
# VCC : 1
# XORCY : 14
# FlipFlops/Latches : 75
# Shift Registers : 8
# SRLC16E : 8
# DSPs : 1
# DSP48E1 : 1
Исходный код
Все узлы формата FP23 написаны на языке VHDL. Для удобства и проверки на С++ написана небольшая программа, которая содержит функции реализуемых операций в плавающей точке на ПЛИС. С её помощью можно проводить отладку и реализацию других форматов с плавающей точкой с другими размерностями экспоненты и мантиссы.
Для удобства чтения данных на VHDL создан тип, определяющий число в формате с плавающей точкой. Все компоненты и типы FP23 собраны в файле fp_m1_pkg.vhd
type fp23_data is record
exp : std_logic_vector(5 downto 0);
sig : std_logic;
man : std_logic_vector(15 downto 0);
end record;
Исходный код RTL-описаний, программа тестирования и результаты синтеза можно найти по ссылке на github.
Тестовый пример
Для тестирования всех разработанных узлов я придумал небольшую схему. Это комплексный умножитель, на входе и выходе которого данные представлены в целочисленной форме, а промежуточные результаты в плавающей точке. То есть входые данные преобразуются в формат FP23. В этом формате реализуется комплексное умножение, а результат переводится назад из FP23 в фиксированную точку. Структурная схема в RTL-Viewer выглядит следующим образом: 
В PlanAhead размещение комплексного умножителя представлено на следующем рисунке. ПЛИС Kintex-7, XC7K70TFBG484–1C.
Видно, что в результате полной трассировки проекта достигается частота обработки порядка ~300МГц. На практике эта цифра на ~30% выше.
В FPGA Editor блок обычного умножителя в формате FP23 выглядит вот так: 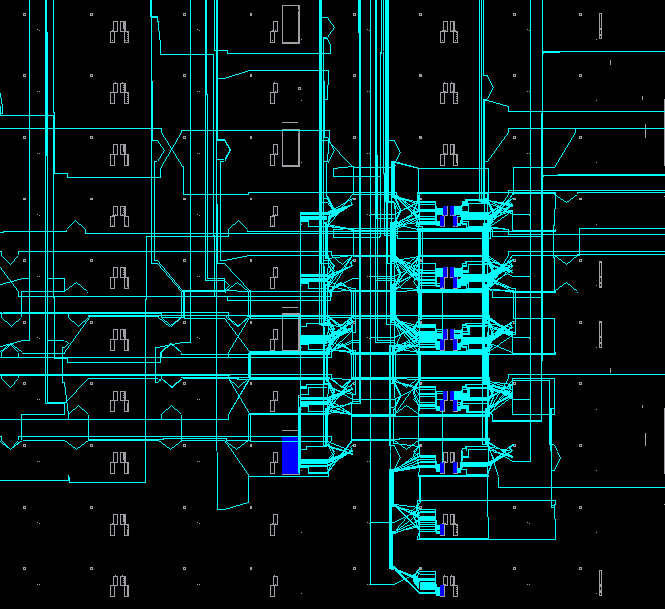
Заключение
В результате работы разработан специализированный формат данных для плавающей точки FP23 на ПЛИС. Он отличается от традиционного формата IEEE 754 и заточен под обработку на ПЛИС на максимальных скоростях. В отличие от стандартных решений от Xilinx и Altera, узлы в формате FP23 занимают значительно меньше ресурсов кристалла. Операции сложения и умножения в FP23 нашли применение для реализации КИХ-фильтров и узла БПФ/ОБПФ на ПЛИС.
При желании вы можете создать собственный формат данных »FP_X» для конкретных задач с произвольной разрядностью мантиссы и экспоненты. При этом необходимо учитывать особенности и структуру конкретных ПЛИС.
Литература
Спасибо за внимание! Продолжение следует…
