Несколько мыслей о сравнении статистики
Сравнение некой сущности с известными объектами — это один из самых очевидных способов классификации. Чем больше объект похож на представителей известного нам множества, тем выше вероятность, что он принадлежит этому множеству. Для сравнения нам нужны конкретные метрики (цифры, пригодные для математической обработки). Но как вы понимаете, визуально анализировать подобные матрицы не очень удобно.
Для удобного восприятия необходимо отобразить эти данные в графическом виде. Первое, что можно попробовать — это «мозаику». Размер её блоков будет отражать значение соответствующей метрики объекта. Так как наша матрица состоит из идентичных объектов, то на общем фоне должен выделяться «странный» объект. Однако, разница его метрик не настолько сильная, следовательно, размеры «странных» блоков не будут радикально сильно выделяться. Лучше всего это можно понять из следующего примера (матрица и её отображение в виде «мозаики»): 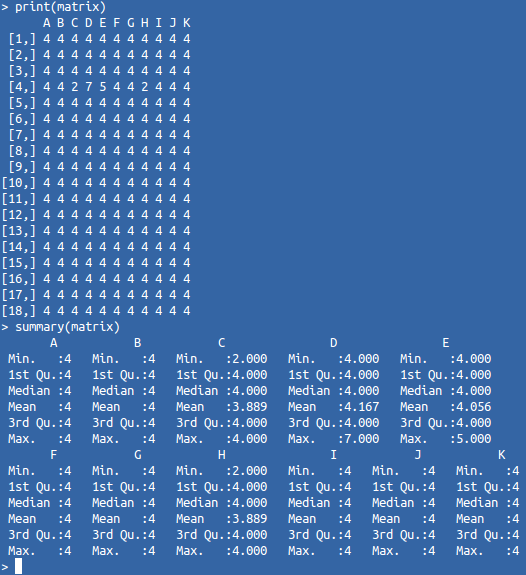
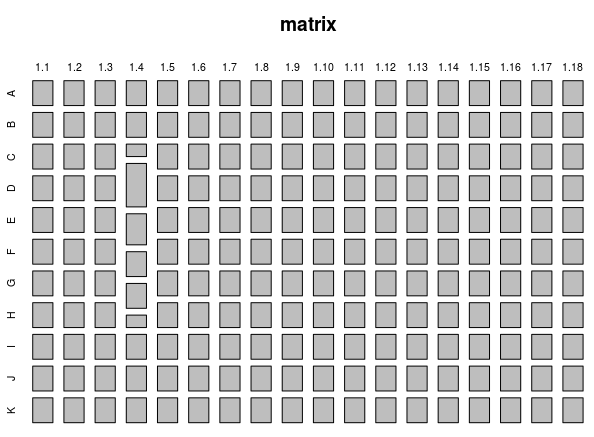
Общеизвестно, что человек может очень быстро находить на однородном фоне отличающийся по цвету объект. Следовательно, если мы отобразим на тепловой карте эту матрицу, то схожие элементы образуют единый фон, а отличающиеся элементы будут хорошо контрастировать с однородным большинством.
Естественно, человек очень хорошо распознаёт не только цвета, но и форму объектов. Если отобразить матрицу в виде трёхмерной перспективы, то любые отклонения от общей массы типичных объектов будут достаточно хорошо видны.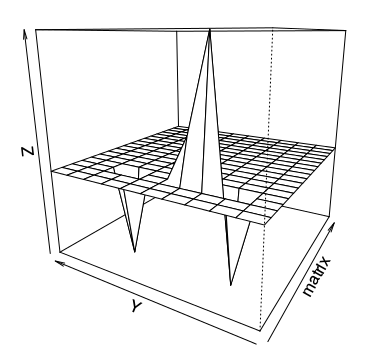
Зная признаки отличающихся объектов можно сформировать подмножество, которое состоит только из «странных» объектов. Далее можно отобразить диаграмму разницы между объектом из подмножества и типичным объектом множества.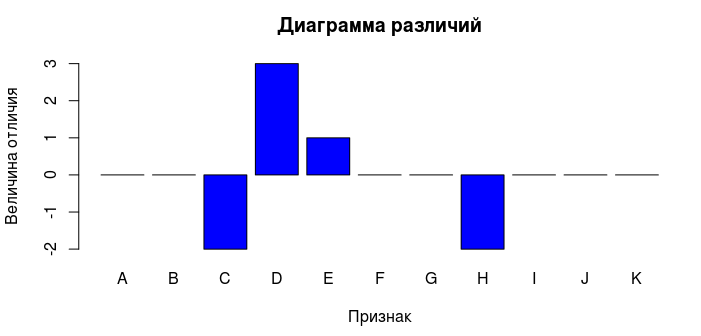
Разумеется, вполне логично будет более подробно изучить поведение интересующих показателей. Как вы знаете, линейный коэффициент корреляции не всегда помогает найти зависимость переменных, однако, мы можем построить график за нужный период времени. Визуально оценить корреляцию будет намного проще. Но мы не просто построим график, а постараемся выполнить элементарный линейный регрессионный анализ. Рассмотрим небольшой пример. Есть гипотеза, что увеличение одного показателя приводит к увеличению зависимого от него значения переменной. Попробуем отобразить это в графическом виде: 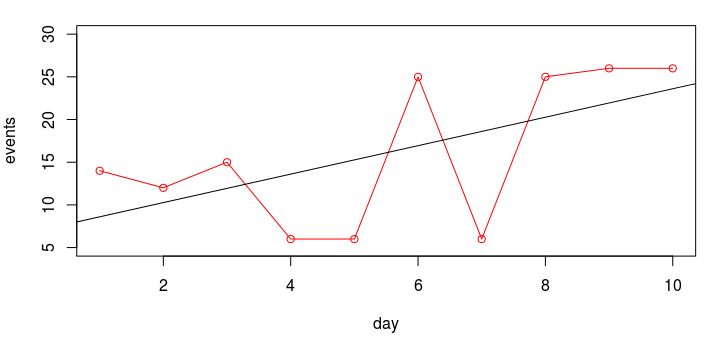
Бывают ситуации, когда мы можем найти сходство по точкам в пространстве. Если отобразить два признака в виде координат (по абсциссе и ординате), то можно заметить, что некоторые точки собираются в группы (образуют кластеры). Мы видим, что точки (A, B, C) собрались в одну группу, а точки (A+, B+, C+) в другую группу. А ещё я добавлю точку Z, которая не должна попасть в ни в один из кластеров. Это такой вот «одинокий волк». Более наглядно отобразить сходства нам поможет иерархический кластерный анализ. Сравним отображение точек на графике и на дендрограмме: 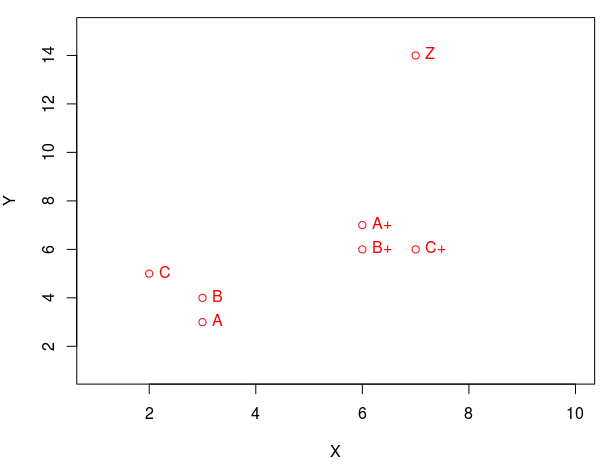
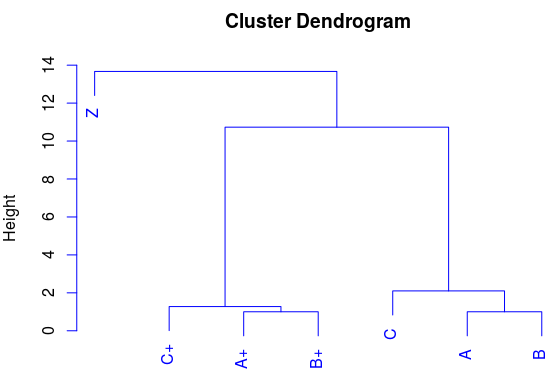
Это достаточно универсальный подход, который не редко используется в визуальной оценке относительно небольших объёмов данных. Многие математические системы уже содержат реализацию упомянутых ранее методов, например, на известном языке программирования R решение подобных задач может выглядеть следующим образом:
# Получение данных из файла
matrix <- as.matrix(read.csv(path), ncol=11, byrow = TRUE)
print(matrix)
summary(matrix)
# Визуальная оценка данных
mosaicplot(matrix)
image(matrix)
persp(matrix, phi = 15, theta = 300)
# Формируем подмножество по заданным условиям
dataset <- subset(matrix, matrix[,"A"] == 4 & matrix[,"C"] < 4 & matrix[,"D"] > 4)
print(dataset)
# Находим и отображаем разницу двух векторов
a <- as.vector(dataset[1,], mode='numeric')
b <- as.vector(matrix[1,], mode='numeric')
diff <- a - b
barplot(diff, names.arg = colnames(matrix), xlab = "Признак", ylab = "Величина отличия",
col = "blue", main = "Диаграмма различий", border = "black")
# Пытаемся найти корреляцию
day <- c(1:10)
events <- c(14, 12, 15, 6, 6, 25, 6, 25, 26, 26)
cor.test(day, events)
plot(day, events, type = "o", ylim=c(5, 30), col = "red")
abline(lm(events ~ day))
# Простой пример кластерного анализа
matrix <- matrix(c(3, 3, 2, 6, 6, 7, 7, 3, 4, 5, 7, 6, 6, 14), nrow=7, ncol=2)
dimnames(matrix) <- list(c("A", "B", "C", "A+", "B+", "C+", "Z"), c("X", "Y"))
plot(matrix, col = "red", ylim=c(1, 15), xlim=c(1, 10))
text(matrix, row.names(matrix), cex=1, pos=4, col="red")
plot(hclust(dist(matrix, method = "euclidean"), method="ward"), col = "blue")
© Megamozg
