Броуновское движение простых чисел
Вы знакомы с броуновским движением: в упрощенном виде его можно рассчитывать так: мы перемещаемся на одну клеточку, а вот направление выбираем случайным образом. Броуновское движение возможно в пространстве произвольных размерностей, для числа размерностей 1 и 2 блуждания почти всегда рано или поздно возвращаются в исходную точку, а для более высоких размерностей это уже не выполняется.
Но что, если мы будем прыгать не на одну клетку, а на очередную разницу между простыми числами — вначале 1 (3–2), потом 2 (5–3), снова 2 (7–5), потом 4 (11–7) итд. А вот направление мы будем 'вращать', например, для плоскости это будет вверх-вправо-вниз-влево? Будет очень красиво.
Сразу скажу, я хотел сотворить что-то красивое с простыми числами с 24 февраля. Это помогало мне не сойти с ума и не выпилиться. Эти эксперименты отвлекали меня, и хорошо, что вначале ничего красивого не получалось — я пробовал и нечто, похожее на игру Жизнь, и треугольник Паскаля, и связь простых чисел и похожих на них lucky numbers… Так что только недавно я получил результат, который меня устроил.
1302 шага, достигнуто простое число 10687
Здесь мы поблуждали совсем недолго, и начали выскакивать за размер небольшого png. Поэтому я решил работать с большими матрицами, а потом 'компессировать' их в картинки приемлемого размера, суммируя число посещений клетки и обозначая это разными цветами.
шагов: 56873, достигнуто простое: 704357
Давайте еще дальше:
шаг: 794673 достигнуто 12108319
Здесь видно, как ведет себя граф: топтание на месте, резкий скачок из-за большого prime number gap. Поехали дальше:
шаг 5'012'197 достигнуто 86'251'189
А что будет, если мы сделаем то же самое для 3d?
3D: шагов 35'778'763 достигнуто 690'345'077
(вид со стороны XY). Внешне все выглядит примерно также. И это не удивительно, если мы не показываем ось Z, то все сводится к плоскому варианту, в котором мы просто пропускаем некоторые шаги. Конечно, если бы размер gap как-то коррелировал бы с номером шага mod 6, то изменения были бы, но гипотеза Римана говорит, что простые числа ведут себя наиболее 'случайным' образом, и такой корреляции не должно быть.
Секундочку, для броуновского движения 2D и 3D случаю различаются принципиально (по вероятности возвращения в данную точку), а с простыми получаются нет разницы от числа измерений? А как с возвращением в точку (0,0)?
Это невозможно по простой причине: первый шаг равен 1, а все остальные шаги четные. Однако не будем занудствовать, какая вероятность того, что блуждание придет достаточно близко к точке 0,0? Давайте построим график расстояния от начальной точки для разного числа измерений:
Миллиард шагов (X), достигнуто простое 22'777'909'477
За исключением 1D, где имеет тенденция касания нуля, остальные графики ведут себя схожим образом, что неудивительно, учитывая что gap все время растет, не говоря о больших выбросах, так что хорошей 'компенсации' плюсов и минусов, как это происходит при броуновском движении, нет (хотя выделенного направления роста, если справедлива гипотеза Римана, тоже быть не может). Сравним с подобным графиками для броуновского движения (конечно, в отличие от детерминированных графиков 'простых блужданий' здесь могут быть разные картины в зависимости от random seed):
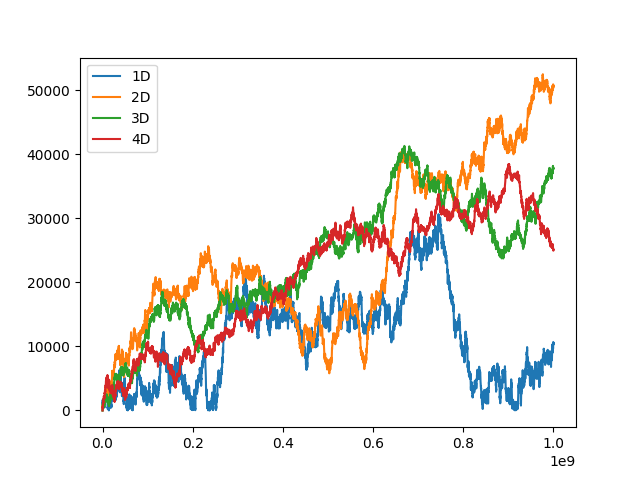Броуновское движение в пространсве разных размерностей
Обратите внимание, что за миллиард шагов мы находимся в пределе 40 тысяч клеток, тогда как для 'простых блужданий' мы ушли в десятки раз дальше.
Ну и в заключение, насколько далеко я могу продолжить расчет? Я достиг на ноутбуке 383'470'718 шагов с матрицей 600'000×600'000 клеток, упакованных в биты, прежде чем блуждание 'вывалилось' за пределы матрицы.
