Бинарная классификация. Проблема равнозначности разделяющих прямых08.02.2023 11:32

При обучении модели классификации объектов (подбор весовых коэффициентов) столкнулись с тем, что проблема НЕ В ТОМ, КАК НАЙТИ разделяющую прямую, а В ТОМ, КАКУЮ ИМЕННО ВЫБРАТЬ из полученного множества разделяющих прямых, одинаково удовлетворяющих условиям классификации.

В итоге пришли к двухступенчатой классификации.

Исходные данные и постановка задачи

В наличии набор объектов, разделенных на 2 класса и с известными характеристиками.

Задача классификации состоит в том, чтобы при получении данных о новом объекте определить, к какому классу его отнести.

Для наглядности пусть у объектов будет по два параметра и пусть это будут, например, жуки и гусеницы с измеренными длиной и шириной.

x_train = np.array([[10, 50], [20, 30], [25, 30], [20, 60], [15, 70], [40, 40], [30, 45], [20, 45], [40, 30], [7, 35]])
y_train = np.array([-1, 1, 1, -1, -1, 1, 1, -1, 1, -1])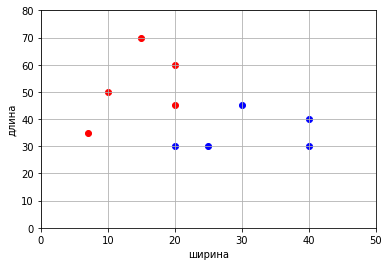

Проблема №1: Наличие множества прямых с нулевой ошибкой

Самое простое, что делают обычно, это разделяют прямой (y = kx+b).

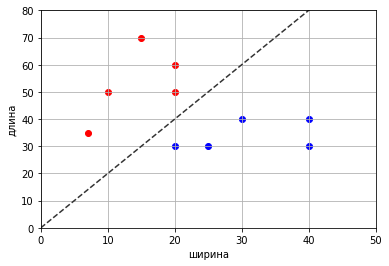
Понятное требование — разделяющая прямая должна быть такой, чтобы разные классы находились по разную сторону от прямой. Тогда все, что «выше» — один класс, а все, что «ниже» — второй класс.

Казалось бы, все просто, и осталось только подобрать коэффициенты, введя известные параметры.

Математически это трактуется так:

def a(x,w): return np.sign(x[0]*w[0] + x[1]*w[1] + x[2]*w[2])
def M(x,w,y): return a(x,w)*y
def Q(w): return sum([1 for index, x in enumerate(x_train) if M(x,w,y_train[index]) < 0])

Если знак a (x, w) совпадает с меткой класса y, то есть отступ M (x, w, y) > 0, то для данного объекта коэффициенты подходят, а если отступ M (x, w, y) < 0, то это ошибка, коэффициенты не походят.

Если сумма ошибок Q (w) по всем объектам равна 0, то коэффициенты подходят.

Пока для простоты и наглядности будем менять только один коэффициент, то есть прямая будет проходит через начало координат. Будем добавлять к коэффициенту один шаг до тех пор, пока суммарная ошибка не станет нулевой.

for n in range(N):
  if Q(w) == 0: break
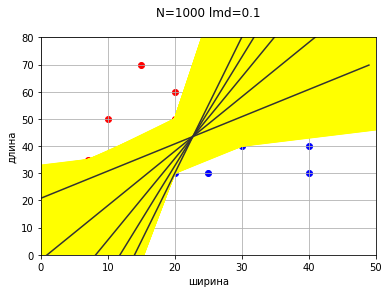
  w[0] = round(w[0] + lmd,4)

Желтые прямые показывают прямую на каждом шаге.
Зеленая прямая — ошибок нет, Q (w) = 0.

На этом этапе прямая соответствует условиям классификации (Q (w) = 0), и вроде бы задача решена и можно заканчивать. Проблема подошла «с другой стороны».

Если не будем останавливаться, когда в первый раз дойдем до прямой с нулевой ошибкой, а пойдем дальше, то получим еще несколько прямых, удовлетворяющих условию нулевой ошибки.

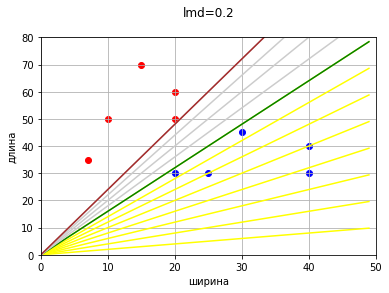
Получается, что есть несколько вариантов проведения разделяющей прямой, и каждый вариант формально будет правильным, так как соответствует критериям классификации и корректно разделяет объекты.

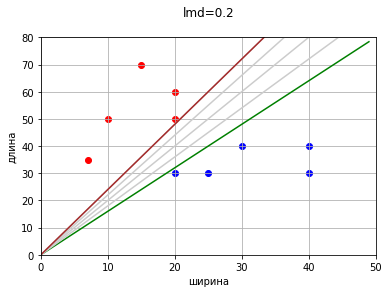
Возникает вопрос: какую именно прямую выбрать?

Будет некорректно выбрать прямую просто так, любую. Потому что когда новый объект попадет между крайними прямыми (зеленой и коричневой), то отнесение его к какому-либо классу будет зависеть именно от того, какая прямая будет выбрана в качестве разделяющей. Довольно сложно будет объяснить заказчику и любому оппоненту, что новый объект с координатами (40,70) отнесется к тому или иному классу исключительно по желанию инженера (программиста).

Значит, нужно вводить дополнительную характеристику, позволяющую убедительно и аргументированно выбрать конкретную прямую из множества прямых с нулевой ошибкой.

Важно отметить, что на данном этапе не рассматривается вопрос оптимизации алгоритма подбора весовых коэффициентов. Градиентный спуск и оптимизаторы — все это важно и нужно и может ускорять подбор в ряде случаев, но у нас здесь нет проблемы найти. Мы уже нашли. Даже не важно как, хоть простым полным циклическим перебором. Проблема в том, как теперь выбрать из множества найденных, одинаково удовлетворяющим критериям.

Проблема №2: Наличие множества прямых с нулевой ошибкой и нулевой разницей средних отступов

Вполне адекватной в качестве дополнительного критерия представляется абсолютная разница между средними значениями отступов. То есть из множества прямых с нулевой ошибкой выберем ту, у которой средние отступы равны или разница между ними минимальна. Звучит логично. Считается сумма отступов объектов класса от прямой, усредняется (делится на количество объектов класса), и если средние отступы равны или разница между ними минимальна, то эта нужная прямая.

Прямая с минимальной разницей средних отступов находится достаточно просто.

x_0 = x_train[y_train == 1]
x_1 = x_train[y_train == -1]

devs = []
devs_w = []

w1_finded = w1[0]
while w1_finded <= w2[0]:
  s_x_0 = sum([(x[0]*w1_finded + x[1]*w[1])*(+1) for x in x_0])/len(x_0)
  s_x_1 = sum([(x[0]*w1_finded + x[1]*w[1])*(-1) for x in x_1])/len(x_1)  
  dev = round(abs(s_x_0 - s_x_1),4)
  devs.append(dev)
  w1_finded = round(w1_finded + lmd,4) 

devs_min = round(devs[np.argmin(devs)],4)
w1_optimum = w1_optimum = round(devs_w[np.argmin(devs)],4)

devs: [14.36, 5.28, 3.8, 12.88, 21.96]
devs_min: 3.8
w1_optimum: 2.0

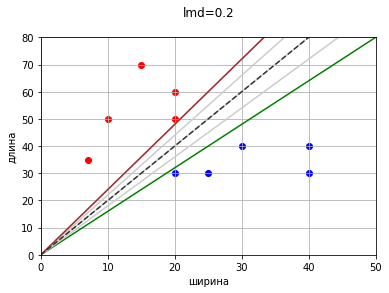
При уменьшении шага разница между средними отступами уменьшается.

devs: [18.9, 14.36, 9.82, 5.28, 0.74, 3.8, 8.34, 12.88, 17.42, 21.96, 26.5]
devs_min: 0.74
w1_optimum: 1.9

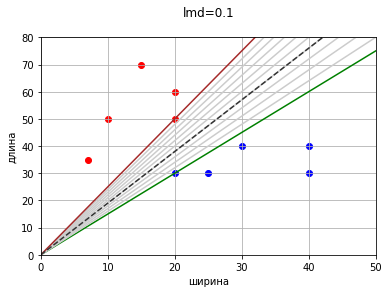
И даже доходит до нуля.

devs_min: 0.0
w1_optimum: 1.9163

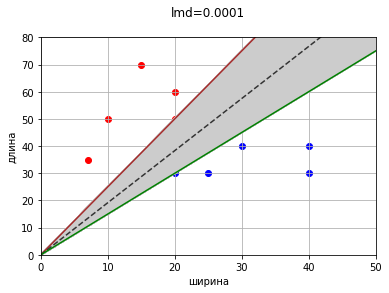
Казалось бы, задача решена, можно заканчивать.
Но нет …

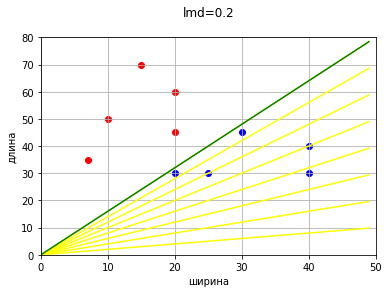
Ведь ранее для наглядности и удобства мы рассмотрели только увеличение одного коэффициента. Если же добавим коррекцию второго коэффициента, то прямых с нулевой ошибкой будет просто огромное множество.

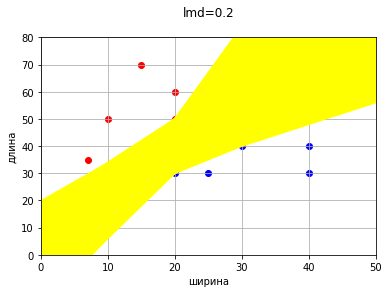
Понятно, что прямые с нулевой ошибкой просто займут всю область между некими крайними прямыми. На данной картинке процесс даже не доведен до конца, так как точки (20,30) и (20,50) лежат на одной вертикали и коэффициенты формально уходят в бесконечность, то есть прямая будет продолжать крутиться против часовой и продолжать закрашивать область.

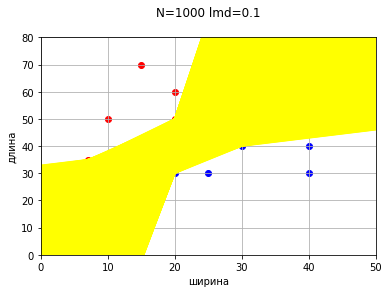
И оказывается, что прямых с нулевой ошибкой и нулевой разницей средних отступов тоже множество.

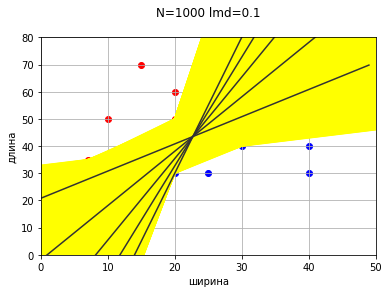
Снова получили множество прямых, удовлетворяющих критериям классификации.

Проблема №3: Производная не вносит ясность

Иногда как вариант предлагается применить дифференцируемую функцию потерь и с помощью производной быстро найти минимум.

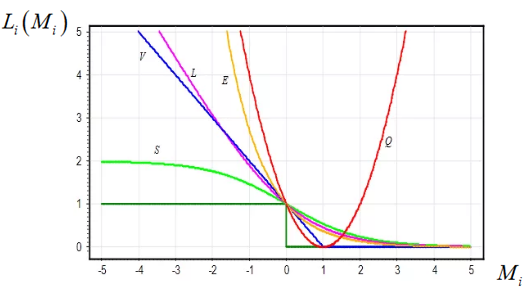
Выберем квадратичную функцию потерь (1-M^2).

Не будем приводить математические преобразования решения уравнения «производная равна нулю», приведем сразу итоговые формулы.

pt = np.sum([x * y for x, y in zip(x_train, y_train)], axis=0)
xxt = np.sum([np.outer(x, x) for x in x_train], axis=0)
w = np.dot(pt, np.linalg.inv(xxt))

Ключевое здесь — «быстро».
Действительно, с помощью решения уравнения «производная равна нулю» коэффициенты находятся практически мгновенно.

w: [ 0.0544658 -0.03886071 0.4540672 ]
y = 1.4016x + 11.6845

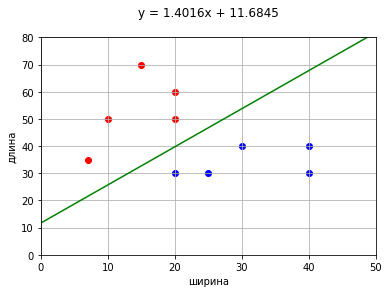
Но ведь это мы нашли всего лишь одну из прямых с нулевой ошибкой. А как видим, прямых с нулевой ошибкой у нас и до этого было целое множество, и подбор с помощью производной не добавляет ясности.

Гарантированный способ: Среднее расстояние до объектов класса

Применим самый «брутальный» подход — классифицируем по среднему расстоянию до объектов класса. В зависимости от того, среднее расстояние до какого класса меньше, к такому классу и относим. Так мы гарантированно определяем, к какому классу будет относится новый объект, размещенный на этих координатах.

def dist(index, index2, label): return sum([ np.sqrt( (x[0] - index)**2 + (x[1] - index2)**2 ) for x in x_train[y_train == label]  ])/len(x_train[y_train == label])

for index in range(max(x_train[:, 0]) + 10 + 1)
  for index2 in range(max(x_train[:, 1]) + 10 + 1):

    dist_0 = dist(index, 0, 1)
    dist_1 = dist(index, 0, -1)

    if dist_0 > dist_1: dist0_massive.append([index,index2])
    if dist_0 < dist_1: dist1_massive.append([index,index2])
    if dist_0 == dist_1: dist_equel_massive.append([index,index2])

Визуально можно представить в виде обозначения точек разным цветом в зависимости от знака между средними расстояниями.

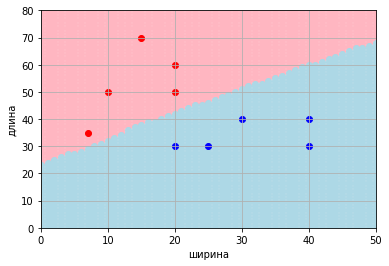
Теперь у нас есть два ряда разделяющих точек:

[[0, 24], [1, 25], [2, 26], [3, 27], [4, 28], [5, 28], [6, 29], [7, 30], [8, 31], [9, 32], [10, 33], [11, 34], [12, 35], [13, 37], [14, 38], [15, 39], [16, 40], [17, 40], [18, 41], [19, 42], [20, 43], [21, 44], [22, 45], [23, 46], [24, 46], [25, 47], [26, 48], [27, 49], [28, 50], [29, 51], [30, 52], [31, 53], [32, 54], [33, 54], [34, 55], [35, 56], [36, 57], [37, 58], [38, 59], [39, 60], [40, 61], [41, 61], [42, 62], [43, 63], [44, 64], [45, 65], [46, 66], [47, 67], [48, 67], [49, 68], [50, 69]]

[[0, 23], [1, 24], [2, 25], [3, 26], [4, 27], [5, 27], [6, 28], [7, 29], [8, 30], [9, 31], [10, 32], [11, 33], [12, 34], [13, 36], [14, 37], [15, 38], [16, 39], [17, 39], [18, 40], [19, 41], [20, 42], [21, 43], [22, 44], [23, 45], [24, 45], [25, 46], [26, 47], [27, 48], [28, 49], [29, 50], [30, 51], [31, 52], [32, 53], [33, 53], [34, 54], [35, 55], [36, 56], [37, 57], [38, 58], [39, 59], [40, 60], [41, 60], [42, 61], [43, 62], [44, 63], [45, 64], [46, 65], [47, 66], [48, 66], [49, 67], [50, 68]]

А для визуализации можно закрасить разделяющие точки одним цветом

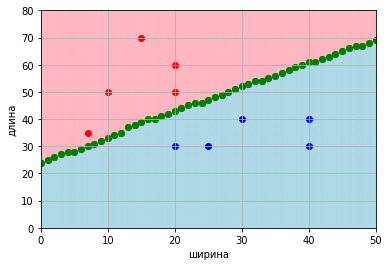
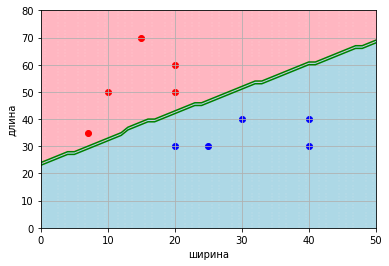
Теперь если объект выше разделяющих точек, то относится к одному классу, а если ниже, то ко второму. И даже если объект попадает на разделяющие точки, то тоже гарантированно классифицируется.

При поступлении нового объекта даже не потребуется вычислений — достаточно сравнить, выше или ниже точка по координате Y при равенстве по координате X.

new = [ [30,30], [10,60] ]

for point in new:

  for key in dist_change_massive: 
    if key[0] == point[0] and key[1] >= point[1]: print(point, 1)

  for key in dist_change_prev_massive:
    if key[0] == point[0] and key[1] <= point[1]: print(point, -1)

[30, 30] 1
[10, 60] -1

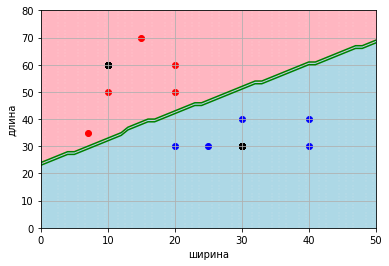
На данном этапе нас все устроило, объекты классифицируются гарантированно, убедительно и аргументированно.

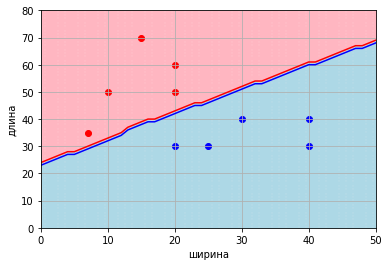
Отдельное продолжение для тех, кто любит аппроксимацию

Получившуюся разделяющую поверхность можно аппроксимировать, например, в прямую.

mx = np.sum(x)/len(x)
my = np.sum(y)/len(x)
a2 = np.dot(x.T, x)/len(x)
a11 = np.dot(x.T, y)/len(x)

kk = (a11 - mx*my)/(a2 - mx**2)
bb = my - kk*mx

ff = np.array([kk*z+bb for z in range(len(x))])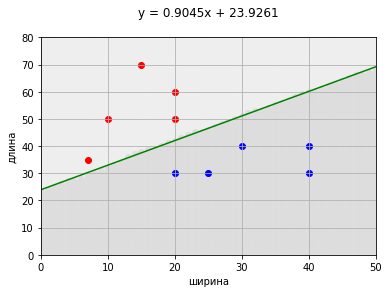

Необходимо отметить, что данная аппроксимированная прямая является прямой с нулевой ошибкой, но не является прямой с нулевой разницей отступов. В самой близи от прямой некоторые точки могут лежать между прямой и разделяющей точками — влияние аппроксимации.

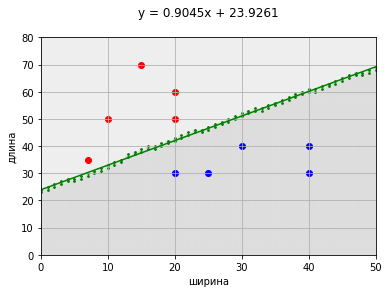
В таком случае целесообразно применять двухступенчатую классификацию:

1. Быстрая классификация
Если объект находится «далеко» от разделяющей прямой, то есть по одну сторону и от разделяющей прямой и от разделяющих точек, то просто сравниваем координаты объекта с координатами разделяющих точек. Никаких дополнительных вычислений не требуется

2. Уточненная классификация
Если объект попадает «очень близко» к разделяющей прямой и оказывается между разделяющей прямой и разделяющими точками, то в этом случае (и только в этом случае!) происходит полный расчет разницы средних расстояний и объект классифицируется по разнице средних расстояний.

При подготовке статьи применялись некоторые данные и формулы с сайта https://proproprogs.ru/, авторам проекта отдельная благодарность)