Байесовский подход к АБ тестированию11.05.2023 13:01

Хабр, привет!

Меня зовут Кристина Лукьянова, я работаю бизнес-аналитиком в компании GlowByte.

Сегодня хочу поговорить об А/Б-тестах, а именно — об альтернативном способе их проведения, который не требует расчета p-value. Так что это за способ и какое применение в нем нашла теорема Байеса?

Два подхода к А/Б-тестам

Суть А/Б-теста заключается в проведении контролируемого эксперимента между сопоставимыми группами для проверки различных гипотез.

Например, мы хотим понять, стоит ли внедрять новую модель подбора предложений. Для этого нужно сравнить конверсии по новой и старой модели. В таком случае в ходе А/Б-теста для одной группы мы делаем предложения по старой модели, для другой — по новой. А далее сравниваем конверсии в группах и принимаем решение о том, какая группа лучше.

Чаще всего в основе А/Б-тестов лежит фреквентистский, или частотный подход. Он основан на расчете значения p-value.

P-value — это вероятность получить значение статистики критерия равное наблюдаемому или более экстремальное по сравнению с наблюдаемым при условии, что верна нулевая гипотеза об отсутствии разницы в группах.

На практике интерпретировать ее можно так: если p-value меньше 0,05 или другого порога, то нулевую гипотезу можно отвергнуть в пользу альтернативной.

Этот подход полезен тем, что:

• для него есть много готовых библиотек;

• мы заранее фиксируем размер выборок, на котором будет виден эффект;

• для принятия решения достаточно только значения p-value.

Несмотря на достоинства частотный подход имеет и ограничения:

• сроки теста фиксированы, «подглядывать» в процессе тестирования не рекомендуется;  

• результат оценивается только бинарно — есть или нет значимые отличия;

• P-value имеет непонятную для бизнеса интерпретацию и не показывает вероятность того, что один вариант лучше другого.

Альтернатива частотному подходу — байесовский. Он делает А/Б-тест более гибким: позволяет не фиксировать сроки теста, использовать более понятные и количественные метрики.

В статистике давно ведутся споры между фреквентистами и байесианцами. Дело в том, что они по-разному смотрят на неопределенность мира.

Фреквентисты предполагают: «Допустим, что мир такой. Тогда какова вероятность, что произойдет это событие?». Для них не важны другие гипотетические миры, где такое же событие могло происходить с другой частотой.

Для байесианцев важны альтернативные миры, они пытаются ответить на вопрос: «Чему равна вероятность того, что мир устроен согласно этой гипотезе?». Поэтому байесианцы рассматривают неизвестные величины как некоторые распределения, а не как точечные оценки.

Алгоритм проведения А/Б-теста по байесовскому подходу

Ниже изображена общая схема проведения А/Б теста по байесовскому подходу.

Рисунок 1. Алгоритм проведения А/Б теста по байесовскому подходу

Рассмотрим пример работы алгоритма на практике — А/Б-тест конверсии. Критерием для принятия решения будет вероятность, что одна группа лучше другой по конверсии.

1. Выбор априорных распределений для конверсий в группе А и Б.

В качестве априорного распределения для каждой из групп возьмем одно и то же бета-распределение: Beta (1,1). В этом случае каждое значение конверсии будет равновероятно как в обеих группах, так и между собой. Поэтому при сравнении конверсий будем опираться только на результаты теста.

Почему в качестве исходного распределения мы берем именно Beta (1,1), я объясню далее, в разделе о теории.

1. Запуск теста и накопление данных.

Начинаем тест и воздействуем на группы по-разному. Спустя неделю теста накоплены следующие результаты:

В группе А: число наблюдений — 30 000, число целевых событий — 100 (конверсия 0,33%).

В группе Б: число наблюдений — 30 000, число целевых событий — 90 (конверсия 0,3%).

Тогда апостериорные распределения можно определить по формуле:

где λ — конверсия, n — число наблюдений, c — число целевых событий, (a, b) — параметры априорной вероятности.

В нашем случае a = 1, b = 1, nA = 30000, cA = 100, nБ = 30000, cБ = 90. Поэтому распределения будут иметь следующий вид:

P (A) = Beta (x, 101, 29 901)

P (B) = Beta (x, 91, 29 911)

На графике видно, что между распределениями конверсий в группах есть разница, но небольшая. Средние значения отличаются на 0,03%, а стандартные отклонения находятся на уровне 0,032–0,033%.

Рисунок 2. Апостериорные распределения конверсий в группе А и Б на 1 неделе (линии — стандартные отклонения)

1. Вычислим значение критерия для принятия решения о разнице в группах. 

Воспользуемся следующей формулой для расчета вероятности, что конверсия в группе Б выше, чем в группе А:

Рисунок 3. Апостериорные распределения конверсий в группе А и Б на 2 неделе (линии — стандартные отклонения)

Выросла и вероятность, что группа А лучше Б по конверсии: с 0,766 до 0,848. Поэтому мы можем быть более уверенными в том, что разница между группами есть.

1. Подведем итоги по прошествии 4 недель.

В таблице приведены результаты за весь срок эксперимента.

К концу 4 недели апостериорные распределения конверсий в группах еще больше «разъехались» друг от друга, а их стандартные отклонения снизились до 0,016–0,017%.

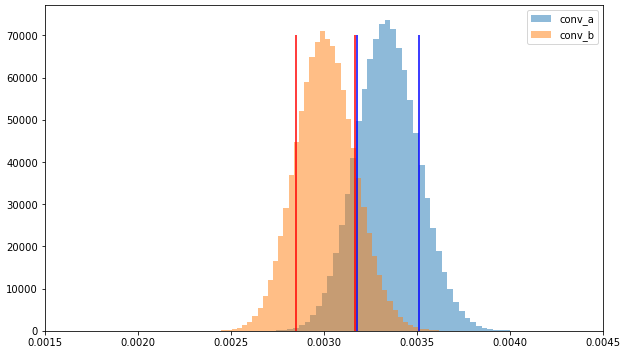
Рисунок 4. Апостериорные распределения конверсий в группе А и Б на 4 неделе (линии — стандартные отклонения)

В конце четвертой недели вероятность, что группа А лучше группы Б по конверсии, стала еще выше — 0,927.

Рисунок 5. Динамика вероятностей, что одна группа лучше другой по конверсии, за 4 недели теста

Итак, чем больше данных мы накопим, тем выше будет уверенность, что между группами есть разница. Это правило работает даже при неизменной разнице в средних конверсиях групп.

Теория

Теперь я подробнее расскажу о теории, которая лежит за полученными результатами.

1 шаг. Выбор априорных распределений для конверсий в группе А и Б

Для начала необходимо выбрать априорные распределения для метрик в группах. Вид распределения может быть любым, но с некоторыми распределениями проще применять теорему Байеса.

Для конверсии удобнее всего применять бета-распределение. Подробнее о причинах этого я расскажу на 4 шаге.

Бета-распределение определяется по формуле:

где

Г — гамма-функция, λ — конверсия.

Часто параметры бета-распределения для априорной вероятности задают как: (a, b) = (1,1), что совпадает со стандартным непрерывным равномерным распределением. То есть предполагается, что мы ничего не знаем о конверсиях до начала эксперимента и обе группы имеют изначально равные шансы на победу.

Альтернативное решение — использовать исторические данные о метриках, чтобы задать априорные вероятности.

Для непрерывных величин вычислять апостериорную вероятность удобно через нормальное распределение.

Если для получения апостериорных вероятностей используются численные, а не аналитические методы, то можно выбирать любые распределения с любыми параметрами.

2 шаг. Запуск теста и сбор данных

Запускаем тест стандартным образом: разделяем выборку на однородные группы, начинаем эксперимент с разным воздействием на группы и периодически собираем данные по конверсии.

Мониторинг стоит проводить часто, например, раз в неделю. Для байесовского подхода важно видеть стабильность результатов в динамике.

3 шаг. Получение апостериорных распределений

Для перехода от апостериорного распределения к априорному можно использовать 2 типа методов:  

• Аналитический — вывод формул на основе теорем и предположений.

• Численный — марковские цепи Монте-Карло и др.

Аналитический метод заключается в выводе формул для апостериорной вероятности на основе теорем и предположений.

Вывод красивых формул возможен, только если мы используем определенные удобные распределения. Например, в случае конверсии это будет бета-распределение.

Если априорные вероятности являются бета-распределениями, то и апостериорные вероятности будут являться бета-распределениями от измененных параметров:

где λ — конверсия, n — число наблюдений, c — число целевых событий, (a, b) — параметры априорной вероятности. 

Это означает, что для перехода от априорной к апостериорной вероятности нужно только два числа — количество целевых событий и общее количество наблюдений.

Мы можем сгенерировать на основе накопленных данных апостериорные распределения для конверсий в 1 и 2 группах, а далее получить их совместное апостериорное распределение для расчета различных метрик:

Совместная апостериорная вероятность задается как произведение апостериорных вероятностей для 1 и 2 групп.

Численные методы — это более гибкий подход, который заключается в подборе апостериорного распределения в ходе итераций.

Методы Монте-Карло для марковских цепей (МСМС) — это методы для получения выборок из вероятностных распределений, которые известны только до некоторой нормировочной константы.

Марковская цепь — это случайная последовательность состояний, где вероятность выбора определенного состояния зависит только от текущего состояния цепи.

Алгоритм МСМС создает и имитирует марковскую цепь. Изначально имеется априорное распределение и накопленные данные эксперимента. Алгоритм выбирает случайное значение из исходной выборки и по определенному правилу принимает или отвергает это значение в зависимости от его соответствия данным и априорному распределению.

Этот процесс повторяется много раз. Первые несколько тысяч шагов алгоритм «прогревается», после чего обычно сходится к апостериорному распределению. На выходе получается большая выборка из распределения.

Пример результата таких итераций изображен на рисунке ниже. Справа — все состояния марковской цепи после того, как она сошлась к апостериорному распределению. Слева представлены гистограммы на основе значений справа, т.е. это распределения для конверсий в группе А, Б и для разницы в конверсиях.

Рисунок 6. Апостериорные распределения конверсий в группе А, Б и их разницы (слева) и итерации для их получения (справа) [2]

4 шаг. Критерии для принятия решения на основе апостериорных распределений

Польза апостериорного распределения в том, что оно не ограничивает нас в критериях для принятия решений. Решение принимается не на основе p-value, а мы можем вывести свои критерии для определения группы-победителя.

Выбор критериев очень широк и зависит от вашей фантазии.

Предлагаю рассмотреть наиболее распространенные критерии принятия решения на основе бизнес-метрики конверсии.

где? — группа А или Б, λА — конверсия в группе А, λБ — конверсия в группе Б,

 — совместная апостериорная вероятность,

L — функция потерь. Она равна 0, если конверсия в группе выше, чем в другой, либо показывает разницу в конверсиях, если конверсия ниже:

Критерий интерпретируется как ожидаемые потери в конверсии с одного пользователя при выборе той или иной группы.

Другими частыми критериями являются среднее и стандартное отклонение аплифта конверсии, Highest Density Interval, Region of Practical Equivalence.

5 шаг. Решение об остановке или продолжении эксперимента

Принятие решения на основе байесовских метрик довольно субъективно.

Можно выбрать некоторые пороги для метрик и принимать решение на их основе. Например, мы уверены в результате, только если вероятность лучшей конверсии в одной из групп больше 0,9.

Есть альтернатива — смотреть результаты в динамике и останавливать тест, когда колебания в метриках становятся низкими. Обычно это происходит по мере накопления данных.

Сравнение фреквентистского и байесовского подходов

Итак, байесовское А/Б-тестирование во многом отличается от фреквентистского. Их основные отличия представлены в таблице. 

Чтобы оценить чувствительность подходов, я провела эксперимент: сравнила мощности байесовского и частотного подходов для разных размеров выборок и различий в группах.

Конверсии я моделировала в виде биномиальных распределений. Базовая конверсия — 10%.

Для байесовского подхода использовала порог 0,95 для вероятности, что одна из групп лучше. Для частотного подхода выбрала порог для p-value — 0,05.

В каждой ячейке — доля экспериментов, когда отличия были значимыми (из 10000 итераций). Ч — частотный подход, Б — байесовский подход.

Результаты сравнения мощности:

Поясню результаты эксперимента на примере ячеек, выделенных зеленым цветом. Для них эксперимент заключался в следующем:  

1. Сгенерировали распределения конверсий: в группе А — со средним 10%, в группе Б — 11% (эффект в 10%).

2. Провели 10 000 итераций: рандомно брали из каждого распределения по 1000 наблюдений, для каждой итерации подводили итог по байесовскому и частотному подходу.

3. Значения в ячейках — доля итераций, где разница была обнаружена (p-value < 0,05 / вероятность, что одна из групп лучше > 0,95). Байесовский подход задетектил разницу в 16% случаев, частотный — в 10%.

По таблице мощностей заметно, что байесовский подход чаще детектил разницу в группах в сравнении с частотным подходом. При больших размерах выборки байесовский подход в 6–7% случаев видит отличия там, где частотный подход их не видит.

Чем байесовские методы могут быть полезны в А/Б-тестах

Одно из главных преимуществ байесовского подхода — это использование более интерпретируемых критериев для принятия решения вместо p‑value. К тому же, байесовские критерии обычно дают количественную, а не бинарную оценку наличия отличий.

Также мы можем останавливать тест в любое время и подводить предварительные итоги. Без фиксации времени теста можно сократить общее время тестирования и ускорить процесс улучшения модели на основе тестов.

Еще одна особенность подхода — результат можно получить на любом объеме данных. На практике бывает, что тест с достаточными выборками провести не получается, а выводы все равно сделать хочется. Там, где p‑value просто скажет об отсутствии статистически значимых отличий, Байес покажет, на сколько большая разница между группами по разным критериям и насколько эта разница вероятна. Но здесь нужно быть осторожным — чем меньше данных, тем меньше уверенность в сделанных выводах.

И последний важный момент — байесовский подход обычно более чувствителен к различиям в группах, что подтверждают результаты эксперимента выше. Ему нужно меньше данных за счет более точного моделирования сравниваемых величин — через распределения, а не точечные оценки.

Так почему, несмотря на свои преимущества, байесовский подход не так широко используется в А/Б‑тестах?

• Дело привычки. P‑value давно и часто используется в А/Б‑тестах.

• Меньше решений на рынке, чем для частотного подхода. Хотя уже есть реализации в крупных продуктах для АБ‑тестов: Growthbook, VWO.

• Требует больших усилий, чем частотный подход: сложнее вычисляется, методика А/Б‑теста менее проработана.

Итак, надеюсь, что вас заинтересовала описанная методика и вы тоже захотите оценить широкие возможности байесовских методов в А/Б‑тестах и не только. Приглашаю в сообщество NoML, где можно обсудить байесовские подходы и другие темы продвинутой аналитики и ML в реальных бизнес‑задачах. Также рекомендую подписаться на наш канал новостей.

Источники:

1. Formulas for Bayesian A/B Testing

2. Bayesian A/B Testing: a step-by-step guide

3. Bayesian A/B Testing at VWO

Дополнительная литература:

1. Is Bayesian A/B Testing Immune to Peeking? Not Exactly

2. How To Do Bayesian A/B Testing at Scale

© Habrahabr.ru