Антивакцинаторы и теория игр, или математические основы антивакцинаторского движения02.07.2021 23:32

Несмотря на злободневность, идея этой заметки родилась задолго до известных событий. Задачка является любопытным математическим этюдом и прямо просится под рассмотрение теорией игр, хотя в этом ключе практически не освещается. Даже люди с хорошим математическим пониманием склонны игнорировать её игровую природу. В прогрессивных кругах при взгляде на людей, выступающих против вакцинации, принято задумчиво хмурится и пожимать плечами, но было бы странно, если бы такое мощное социальное явление не имело под собой никаких фундаментальных основ. Есть ли в отказе от прививок рациональное? Большинство заявлений антивакцинаторов не имеют под собой никаких оснований, но причины поступков человека часто не совпадают с тем, что он декларирует. В этой статье я немножко поиграю с математической моделью конфликта и покажу, почему антивакцинаторство необоримо. Если вы заинтересовались, прошу к тексту.

Не будет преувеличением сказать, что движение против вакцинации зародилось практически сразу после изобретения Эдвардом Энтони Дженнером первой вакцины от оспы (первый эксперимент на человеке — 1796 год). За двести с лишним лет технология вакцинации доказала свою работоспособность и, более того, отметилась немалыми достижениями, в частности, победой над оспой, корью, полиомиелитом и другими болезнями. Однако, несмотря на эти неоспоримые достижения, на вакцины люди поглядывают с опаской. Может ли математическое описание задачи помочь нам разобраться с этим казусом?

Предлагаемая в статье матмодель довольно примитивна и сильно упрощена. Она игнорирует территориальную и временную динамику, но зато демонстрирует качественный феномен — зачем и откуда взялись люди, которые вакцинироваться не хотят. Надо сразу оговориться, что графики, приведённые ниже, если не сказано обратного, построены на основе величин «взятых с потолка» с единственной целью продемонстрировать качественные эффекты. Это сделано с умыслом: на взятых по реальным болезням данных изучаемые в статье эффекты оказываются исчезающе малыми и совершенно не наглядны. Тем не менее, существуют причины, делающие понимание этих эффектов важным. Эти причины мы обсудим сразу же после анализа матмодели.

Качели сомнений.

Постановка задачи. Пусть на планете Шелезяка существует популяция роботов, которой угрожает компьютерный вирус. Инженеры Шелезяки изобрели программный патч. Патч замедляет распространение вируса, проникшего через файрвол робота, помогает антивирусному софту робота лучше опознавать и уничтожать вредоносный код, снижает шанс передачи вируса роботу-соседу. Существует вероятность, что из-за особенностей индивидуального программного или аппаратного обеспечения патч может работать не совсем корректно и вызывать некоторые нежелательные явления, но не защищённые патчем и поражённые вирусом роботы имеют существенные проблемы, вплоть до возможности перемещения в сторону свалки под печальную музыку. Известно также, что чем больше заражённых вокруг робота, тем выше шанс заразиться самому, причём, если пропатчатся все роботы, шанс заразиться станет исчезающе мал. Каждый робот должен принять решение — ставить ему программный патч, или нет. Спрашивается: Какова оптимальная стратегия робота-игрока в таких условиях?

Рассмотрим способ мышления робота при выборе обществом тривиальных стратегий:

Я не патчусь и никто не патчится. Вирус бушует, многие умерли. Опасно. Буду ставить патч.
Все ставят патч. Вирус уничтожен, эпидемия побеждена, не начавшись. Превосходно. Однако, если я поставлю патч, я могу поиметь неблагоприятные явления, пусть даже вероятность их мала. В то же время риска заразиться нет, так как все поставят патч. Не буду ставить патч.

Эти классические качели означают, что задача не имеет решения в чистых стратегиях. Даже исчезающе малая вероятность получить нежелательные явления при достаточно большой популяции способна привести в движение качели и запустить игру.

Теория игр и камрад Джон Нэш говорят нам, что если решений нет в чистых стратегиях, его надо искать в стратегиях смешанных. Смешанная стратегия предполагает, что игрок действует стохастически и с некоторой вероятностью или ставит патч, или не ставит. Верность этого соображения может быть показана на дифференциальных уравнениях динамической модели системы. Действительно, если роботы принимают решение один за другим и имеют полную информацию о решениях, принятых предыдущими сопланетниками, они могут внимательно смотреть на то, какое количество роботов пропатчилось. Робот будет патчиться, если пропатченных становится мало, и отказываться от патча, если пропатченных становится много. Этот процесс довольно быстро приходит к некоторому устойчивому равновесию, и тогда можно определить шанс встретить пропатченного робота или, что то же самое, долю пропатченных роботов в популяции.

Перечислим действующих лиц этой изумительной театральной постановки:
$p$ — Вероятность, того что робот поставит патч (это наш главный герой).
$v$ — Вероятность для робота быть заражённым вирусом (а это персонаж трикстер).

Дальше идут статисты и герои второго плана:
$q$ — Вероятность получить нежелательные явления при установке патча.
$w$ — Вероятность тяжелого поражения вирусом для заражённого непатченного робота.
$r$ — Коэффициент снижения вероятности заражения пропатчившегося робота.
$e$ — Вероятность тяжелого поражения вирусом для заражённого пропатченного робота.
$Q$ — Штраф получаемый роботом, если ему не повезло с патчем.
$W$ — Штраф получаемый непатченным роботом, если ему не повезло с вирусом.
$E$ — Штраф получаемый патченным роботом, если ему не повезло с вирусом.

Необходимо оговорится, что более сложная модель должна была бы включать в себя влияние патча на разные события, как то — шанс проникновения вируса через файрвол, шанс исполнения проникшего вируса (то есть перехода его в активную форму), шанс получения существенного урона, и, наконец, шанс распространения вируса заражённым роботом. На каждую из этих вероятностей и сопутствующих им штрафов и эффектов патч влияет по-разному, но в нашей примитивной модели мы ограничимся несколькими совокупными характеристиками.

Представим ещё одного важного персонажа нашей драмы. Применяя формулу полной вероятности, распишем риск $S$ , получаемый среднестатистическим роботом в зависимости от доли патченных роботов в популяции $p$ (Напомню, что риском по определению называется произведение штрафа на вероятность его получения).

$ S = p v (q Q + r e E) + p (1-v) q Q + (1-p) v w W + (1-p)(1-v) 0$

или,

$S(p) = p x(p) + (1-p) y(p) \\ x(p) = qQ+v(p)reE \\ y(p) = v(p)wW$

Здесь мы видим еще двух героев:
$x(p)$ — совокупный риск патченного в зависимости от доли пропатчившихся.
$y(p)$ — совокупный риск непатченного в зависимости от доли пропатчившихся.

Это те самые риски, которые взвешивает робот, принимая индивидуальное решение. Особо отметим, что робот обязан выбрать один из двух вариантов, то есть пойти или на риск $x$ , или на риск $y$ . Отказаться играть в игру робот не может.

Разность рисков как функция доли пропатчившихся, это последний по списку, но не по значимости, участник труппы:

$ s(p) = y(p) - x(p) $

Функции $s(p)$ и $S(p)$ интересны тем, что первая отвечает за чаяния индивидуальные, а вторая за чаяния общественные. Далее мы увидим, разделяет ли общество интересы собственных индивидов, и блюдут ли индивиды интересы общества.

В поисках равновесия.

Попробуем прикинуть поведение зависимостей $x(p)$ и $y(p)$ .

В простой модели, не учитывающей всяческих побочных и социальных явлений, до рассмотрения которых мы дойдём позже, риск побочных явлений $q Q$ выглядит как константа, ибо зависит только от качества патча, но не от доли патченных.

Коэфициенты $w$ , $r$ , $e$ , $W$ , $E$ также будем считать константами.

Величина $v(p)$ есть вероятностью робота заразиться с вирусом. Зависимость $v(p)$ не слишком физична, ибо зависит от кучи разных факторов помимо доли пропатчившихся. Но некоторые предположения о её виде в рамках модели первого приближения сделать можно. Из условия следует, что функция не возрастает, то есть характеризуется неположительной первой производной $dy/dp \le 0$ . Вероятно она имеет вогнутый вид, то есть вторая производная неотрицательна $d^2y/dp^2 \ge 0$ . Кроме того, дано, что можно свести болезнь в ноль при $p_{иммунитет} = 1$ или даже при некотором $p_{иммунитет} < 1$ (см. популяционный иммунитет).

Чтобы иметь возможность построить какие-нибудь графики, рассмотрим семейство функций $v(p)$ , удовлетворяющих заявленным выше характеристикам. Пусть $v(p)$ имеет следующий вид:

$ v = v_0 (1 - p) ^ n $

Код графика

#!/usr/bin/env python3

import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import numpy

def find_minimum(S):
    minidx = 0
    for i in range(len(S)):
        if S[i] < S[minidx] : minidx = i

    return minidx

p = numpy.linspace(0,1,1000)

def vn(v0, n):
    return v0 * (1-p)**n

fig, ax = plt.subplots()

ax.set_xlabel('доля патченных p')
ax.set_ylabel('вероятность быть атакованным v(p)')

ax.plot(p, vn(0.1, 1), p, vn(0.1, 1.5), p, vn(0.1, 2), p,  vn(0.1, 3))
ax.grid()

ax.legend(["0.1(1-p)", "0.1(1-p)^1.5", "0.1(1-p)^2", "0.1(1-p)^3"])
plt.show()

Подобрав некоторые константы матмодели $q$ , $w$ , $r$ , $e$ , $Q$ , $W$ , $E$ для получения красивой картинки, посмотрим на графики функций $x(p)$ , $y(p)$ , $S(p)$ .

Код графика

#!/usr/bin/env python3

import matplotlib.pyplot as plt
import matplotlib.lines as mlines
import numpy

def find_minimum(S):
    minidx = 0
    for i in range(len(S)):
        if S[i] < S[minidx] : minidx = i

    return minidx

p = numpy.linspace(0,1,1000)

def v(p):
    return 0.3 * (1-p)**1.5

def x(p):
    return 0.08 + 0.1 * v(p)

def y(p):
    return 1 * v(p)

def S(p):
    return p*x(p) + (1-p)*y(p)

S_minidx = find_minimum(S(p)) 

fig, ax = plt.subplots()

ax.set_xlabel('доля патченных p')

ax.plot(p, x(p), p, y(p), p, S(p))
ax.scatter([p[S_minidx]],[S(p)[S_minidx]],color="darkgreen",marker="D")
ax.grid()

ax.legend(handles=[
mlines.Line2D([], [], color='blue', label='x(p)=0.08 + 0.03(1-p)^1.5'),
mlines.Line2D([], [], color='orange', label='y(p)=0.3(1-p)^1.5'),
mlines.Line2D([], [], color='green', label='S(p)=p*x(p) +  (p-1)*y(p)'),
mlines.Line2D([], [], color='darkgreen', marker='D', linestyle='None',
                         markersize=10, label='S_minimum')
])

plt.show()

На графике сразу бросаются в глаза две точки — точка пересечения кривых $x(p) = y(p) = S(p)$ и точка минимума $S(p)$ , отмеченная зелёным ромбом. Точка $p_{опт} = argmin(S(p))$ соответствует такой замечательной стратегии при которой среднестатистический робот получает наименьший риск и наибольшее благоденствие. Это лучшая стратегия, которую мог бы выдумать для группы коллективный разум. Интересно отметить, что наибольшее благоденствие достигается отнюдь не при ста процентах пропатченных. Если сделать допущение, что $r$ стремится к нулю, несложно произвести аналитический расчёт экстремума функции $S(p)$ для выбранной к рассмотрению семейства функций $v(p)$ из условия $dS(p)/dp = 0$ :

$S(p) = pqQ + (1-p)v(p)wW \\ S(p) = pqQ + v_0(1-p)^{n+1}wW \\ \frac{dS(p)}{dp} = 0 : qQ - v_0 wW (n + 1) (1 - p)^n = 0 \\ \frac{qQ}{v_0wW(n + 1)} = (1 - p)^{n} \\ p = p_{опт} = 1 - \sqrt[n]{\frac{qQ}{v_0wW(n + 1)}}$

Если подкоренное выражение меньше единицы, функция $S(p)$ имеет экстремум в области определения $p\in[0,1]$ . Поиграться с конкретными значениями и зависимостями можно с помощью кода, который приложен к графику. При $r \neq 0$ аналитический расчёт существенно усложняется, поэтому оставим его за скобками изложения.

Но, самое интересное в приведённом графике не то, что минимум среднестатистического риска достигается отнюдь не при ста процентах пропатченных, а то, что положение группового оптимума $p_{опт}$ не является равновесным. Действительно. Обратим внимание, что $$x(p_{опт}) > y (p_{опт})$» />. Из этого следует <img src=$ . Это значит, что если роботы выбирают установку патча с вероятностью $p_{опт}$ , роботу-индивидуалисту выгоднее будет отказаться от установки патча.»Да, отлично, мы достигли оптимального количества патченных, но мои риски будут меньше, если я откажусь от установки патча, я же умный». А поскольку умных много, совокупная доля пропатчившихся тут же начинает падать, и продолжается это падение до того момента, пока $x(p)$ не сравняется с $y(p)$ , то есть система съезжает в точку схождения кривых, где качели уравновешиваются.

Странный эффект бесполезного патча.

Прежде чем продолжить движение по рельсам анализа, хочется рассмотреть один интересный неинтуитивный эффект. Сравним графики при изменении параметра $reE$ при его стремлении от $0$ к $wW$ . В ситуации, когда $reE = 0$ , патч полностью защищает робота от заражения. Если $reE = wW$ , патч не помогает роботу легче переносить болезнь и вообще никак не улучшает его жизнь в случае, если робот заразится. Думаете, при патч бесполезен и роботы откажутся его использовать? Ну, почти:

Сравним первый ( $reE = 0.1$ ) и второй ( $reE = 0.5$ ) графики. По мере увеличения параметра $reE$ точка схождения кривых, характеризующая положение качельного равновесия, действительно смещается влево — всё большее количество роботов отказываются от патча, но обратите внимание, что групповой оптимум, напротив, смещается вправо!

Эмм… Кажется с нашей матмоделью что-то не так. Почему бесполезный для индивида патч стал более полезным для группы? Фокус тут в том, что патч не бесполезен. Да, он меньше помогает заражённому, но вероятность установки патча по-прежнему участвует в зависимости $v(p)$ . Чем больше $p$ , тем меньше заражённых, то есть патч препятствует распространению болезни. Его установка всей популяцией является единственным способом минимизировать потери группы, но чем меньше индивидуального профита даёт патч, тем меньше роботы склонны к его установке. Апофеоз достигается на третьем графике при $reE = wW$ , то есть, когда патч не помогает индивиду переносить болезнь. Мало того, индивид еще и платит за его установку риском $qQ$ ! На всей области определения и не могут точно определить $p_{опт}$ , но зато наличие статистики помогает прикинуть соотношение рисков $x(p_т)$ и $y(p_{т})$ , где $p_{т}$ соответствует доле патченных на текущий момент. Как определить, находится ли текущая ситуация в точке равновесия или в точке оптимума? Если $p_т \neq p_{опт}$ , мы должны иметь ненулевой градиент $S(p)$ .

$S(p) = p x + (1-p) y(p) \\ \frac{dS(p)}{dp} = 0 \\ x(p) - y(p) + (1-p) \frac{d(y(p))}{dp} = 0$

Определение этой характеристики требует понимания вида зависимости $y(p)$

, а потому осложнено. А вот с качельным равновесием проще.

Нахождение в точке качельного равновесия вычисляется из условия:

$s(p_т) = y(p_т) - x(p_т) = 0 \\ v(p_т) ( w W - r e E ) - q Q = 0$

Проанализируем «физический смысл» левой части последнего выражения. Первое слагаемое характеризует отличие того насколько хорошо патченный и непатченный роботы переносят вредоноса, помноженные на вероятность получить этого самого вредоноса, а второе слагаемое характеризует риск получить нежелательные явления при установке патча.

Возвращаясь с Шелезяки на Землю и, вооружившись матмоделью, очень хочется как-то уложить в неё имеющуюся в инфопространстве статистику. Дело это не то чтобы сильно благодарное. Для этого нужно расчитать вероятности и определить штрафы, то есть подсчитать риски. Это легко сказать, «посчитать риск», но как сравнить штраф выраженный в виде головной боли со штрафом в виде летального исхода? Впрочем, большой точности от нас никто не потребует, а качественную оценку попробуем получить, отталкиваясь от понятной и выраженной в числах категории смертности.

Пусть $Q = W = E = 1$ .
О модели заразности у нас данных особо нет, хотя теоретически можно посмотреть долю новых случаев в популяции для разных стран и построить зависимость от количества вакцинированных. Но, поскольку автор статьи очень ленив, примем нашу модельную зависимость $v(p)=v_0(1-p)^{1.5}$ .

$v_0$ — оценим как вероятность заразиться коронавирусом по официальным данным (Я взял приблизительную статистику по России на момент написания статьи: ссылка): $v_0 = \frac{число\_заражений}{население\_страны} = \frac{5000000}{144000000} = 0.0347$
$w$ — шанс смерти заражённого по тем же данным $w = \frac{число\_смертей}{число\_заражений} = \frac{135000}{5000000} = 0.027$
$r e$ — шанс смерти вакцинированного от вируса. Если, например, оттолкнуться от результатов третьей фазы испытаний вакцины Спутник V (ссылка), можно почерпнуть, что из группы добровольцев, состоящей из 14 964 человек, которые получили укол настоящей вакцины, в итоге заболели 16 человек, или 0,1% тех, кому ввели препарат. В группе плацебо, в которую вошли 4902 человека, заболели 62 человека — 1,3% тех, кому ввели физраствор. Если даже забыть, что вакцинированные болеют легче, $re$ получается не менее чем в 13 раз меньше $w$ . $r = 1 / 13$ , $e = w$ .
$q$ — С $q$ всё ещё интереснее, ибо, хотя данные по каким-то серьёзным последствиям вакцинации есть, проверка подавляющего большинства сообщений показывает отсутствие реальной причинно-следственной связи. Что до подтверждённых случаев даже не смертей, но тяжелых реакций, их количество оценивают примерно как один на миллион. $q = 10^{-6}$ . Вот, например, со слов РИА новостей (Ссылка) количество тяжелых реакций в Буэнос-Айросе при эксплуатации вакцин «Спутник V», «Sinopharm» и «Covishield/AstraZeneca» составило 0,7, 0,8 и 3,2 на миллион соответственно.

Но оценивать последствия $qQ$ только по летальным случаям и тяжелым реакциям всё же неправильно. Как же головная боль, нарушение сна, повышенная температура которые настигают после вакцинации почти всех. Давайте не будем останавливаться только на оценке $q=10^{-6}$ , но посмотрим также $q=10^{-5}$ , $q=10^{-4}$ , то есть увеличим эту оценку в 100 раз. Вот результаты.

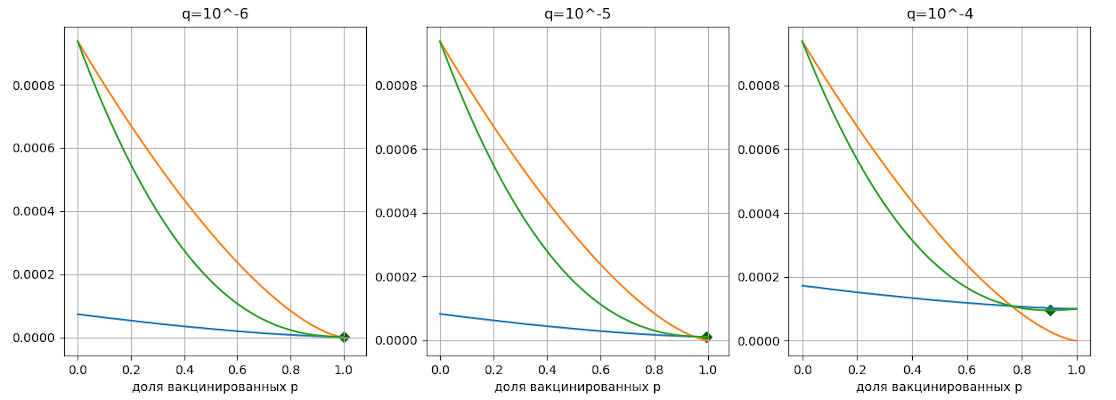
Ну, ок. Подняли в сто раз — получили какое-то смещение. И даже так оптимум и точка группового равновесия сильно смещены вправо от той доли вакцинированных, какую мы имеем сегодня. Разность $s(p_{текущее})$ вопиюще большая!

Получается, система находится сильно левее не то что группового оптимума, но даже положения качельного равновесия. Стремится к этому самому равновесию система, как кажется, даже не собирается. Что происходит? В каком месте математическая модель даёт сбой?

Почему теория игр не работает? Иррациональность рациональность.

Вопрос, который надо задать при применении любой математической модели к объектам реального мира — «а действительно ли объекты ведут себя так, как предсказывает теория и почему нет?». В мире Шелезяки информация дана в виде размазанной статистики, искажённой интерпретаторами и собственным восприятием робота. Робот строит оценку рисков не на основе реальных данных, но на основе реконструкции реальных данных по анализу данных имеющихся и строит не то чтобы сильно качественно. В ситуации, когда взвешиваются две величины, причём одна сильно больше другой, робот склонен переоценивать значимость меньшей. Если робот сравнивает вес шайбы М8 и токарно-карусельного станка, он понимает, что станок должен быть тяжелее шайбочки, но степень этого тяжелее представляется роботу довольно туманной. Кажется, что раз мы взвешиваем два риска (а мы их взвешиваем, ведь игра не просто началась, но активно происходит прямо здесь и сейчас), между ними хочется найти хоть какую-то сопоставимость. При принятии решения, робот, подтягивает значимость рисков друг к другуон склонен недооценивать вред вируса, и переоценивать вред патча.

Кроме того, помимо оценки рисков самих патча и вируса, в реальном расчёте должны быть учтены и такие странные факторы как социальные риски (R7-D8 будет меня уважать, если я поставлю патч, а HK-553, если узнает, подбросит мне загуститель в машинное масло), неудобства связанные с процессом постановки патча (пункт техобслуживания в соседнем городе, пока доеду — развалюсь) и даже преимущества от получения листа технической неисправности (заражусь и можно будет не ехать на нелюбимую работу, а вместо этого заценить третью серию сериала о биологических мешках, посягающих на независимость Шелезяки). Кажется, что социальные факторы в этой задаче избыточны, но на практике значимость их не просто сопоставима, но может в разы превышать значимость основных эффектов игры, и в обществе победившего мракобесия биологически-технический профит патча может оказаться менее значимым, чем риск общественного порицания!

Поскольку наша модель примитивна, аки дихотомия добра и зла, все роботы имеют один и тот же набор имеющихся данных и сопутствующих факторов, и выполняют одну и ту же реконструкцию. В результате этой работы они строят равновесную стратегию. Назовём равновесие достигаемое такой стратегией — «равновесием по реконструированным данным и сопутствующим факторам» в противовес «равновесию по полной информации», полученному нами ранее.

$x_и(p) = x(p) + x_e(p) + x_s \\ y_и(p) = y(p) + y_e(p) + y_s \\ S_и(p) = px_и(p) + (1-p) y_и(p)$

Дополнительные слагаемые учитывают ошибки прямых оценок рисков $x_e$

,

и риски сопутствующих обстоятельств $x_s$

,

.

Интересно так же заметить, что общественное мнение по вопросу, «а каким должно быть ?» не так чтобы скореллировано с самим $p$ : «Надо роботов патчить — надо. Будешь патчиться — чего, я дурак что-ли?». Противоречащие личная и общественная установки прекрасно уживается в одном кремниевом вычислителе (вспоминаем дихотомию группового оптимума и качельного равновесия).

Конкретный вид зависимостей $x_e, x_s, y_e, y_s$ для нашего сугубо качественного анализа большой роли не играет, а интересует нас только то, что роботы реальной картины не ведают, склонны к переоценке малых рисков, а при принятии решений принимают во внимание кучу всякой бесполезной фигни дополнительную важную социальную информацию. На основе этих данных роботы строят равновесную стратегию, которая смещена как относительно группового оптимума, так и относительно качельного равновесия по полной информации. Баланс этой стратегии может быть существенно смещён. Если вред вируса недооценивается, а вред патча преувеличивается, в системе происходит что-то такое:

Реальная игра ведётся не реальном, но в воображаемом пространстве, в имаджинариуме самих игроков. Важно понимать, что стратегия о которой сейчас идёт речь — это равновесная стратегия, пусть она и оторвана от положения дел в реальном мире. Никаких оперативных механизмов обратной связи, способных сместить баланс к более физичному состоянию, в системе не наблюдается. При этом, несмотря на наличие дополнительных слагаемых, вид «искажённых» уравнений и графиков мало чем отличается от вида уравнений, которые мы получали ранее при анализе системы с полной информацией. Родственность искажённой и неискажённой систем тонко намекает нам на то, что искажённая система в целом живёт по тем же законам, что и неискажённая. Именно это соображение заставляет внимательно относиться к изученным выше эффектам, несмотря на то, что для истинной системы влияние их исчезающе незаметно.

Темпоральные стратегии.

Было бы неправильно обойти вниманием интересную, обсуждаемую в последнее время стратегию, выходящую за рамки нашего анализа. Или, вернее две довольно рациональные стратегии.

»Из разных источников поступает противоречивая информация. Патч то ли работает, то ли нет. Ничего не понятно, рационально будет подождать.»
»Я хочу патч, но не верю нашим инженерам. Подожду, пока не появится альтернативный патч от разработчиков с Кибертрона».

Обе стратегии выходят за рамки примитивной модели, потому что апеллируют к идее ожидания, то есть к понятию времени, не учтённому в вероятностной модели. Можно ввести эти стратегии в модель чисто декоративно.»Поставлю патч, но позже» опишем как некоторую вероятность для игрока быть поражённым в момент бездействия. Такая вероятность есть функция от доли патченных $p$ и времени бездействия $h$ . Стратегию альтернативного патча можно описать как разные риски, символизирующие патчи от разных инженеров и разные вероятности их получения. Отметим, что нет никаких гарантий, что патч А существенно лучше патча Б, но, если бы нам были бы известны оценки всех рисков, мы бы пожалуй могли бы посчитать, сколько времени имеет смысл ждать, чтобы профит от возможности поставить более качественный патч превзошёл риск от ожидания альтернативного варианта. Оставим задачу вывода этой зависимости в качестве упражнения для тех, кому нечем заняться вечером.

Не забудьте учесть, что правильный расчёт подразумевает учёт как рисков побочных явлений $qQ$ , так и профит в деле борьбы с болезнью $v(wW - reE)$ , причём второе слагаемое для реальных препаратов окажется в разы существенней первого и именно его в первую очередь надо принимать во внимание. Бывает и такое, что анализируют препарат только с точки зрения риска нежелательных явлений. Несомненно, самой лучшей прививкой является физраствор.