[recovery mode] Ханойские башни — теоретическое решение без рекурсии
Задача Ханойских башен — одна из самых первых задач, которые предлагаются начинающим программистам, в основном, чтобы проиллюстрировать концепцию рекурсивных решений. В этой статье приводится метод, который позволяет теоретическим путем, без рекурсии, указывать оптимальное решение для текущего хода.
«Ханойская башня» является одной из популярных головоломок XIX века. Даны три стержня, на один из которых нанизаны восемь колец, причем кольца отличаются размером и лежат меньшее на большем. Задача состоит в том, чтобы перенести пирамиду из восьми колец за наименьшее число ходов на другой стержень. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее.
Классическое решение данной задачи с тремя стержнями предполагает, что для заданного количества колец n количество перекладываний вычисляется по формуле.
Дополнительную привлекательность данной задаче придаёт и сопровождающая её легенда:
В Великом храме города Бенарес, под собором, отмечающим середину мира, находится бронзовый диск, на котором укреплены 3 алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времён, монахи этого монастыря провинились перед богом Брахмой. Разгневанный Брахма воздвиг три высоких стержня и на один из них возложил 64 диска, сделанных из чистого золота. Причем так, что каждый меньший диск лежит на большем. Как только все 64 диска будут переложены со стержня, на который Брахма сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.
Между делом новичку предлагается оценить сложность данного решения, чтобы впечатлить результатом: число перемещений дисков, которые должны совершить монахи, равно 18 446 744 073 709 551 615. Если бы монахи, работая день и ночь, делали каждую секунду одно перемещение диска, их работа продолжалась бы 584 миллиарда лет.
Суть решения сводится к пониманию того, что для перемещения текущего диска необходимо решить задачу по переносу всех предыдущих дисков на свободный стержень, перемещению требуемого диска и последующему обратному перемещению всех предыдущих дисков меньшего размера на нужный стержень. Таким образом, решение задачи сводится к предыдущим решениям, что и иллюстрирует механизм рекурсии.
Александр Бусаров MrShoor написал очень информативный пост, отлично дополняющий соответствующую статью в Википедии, с очень подробным программным кодом, рекомендую ознакомиться с его реализацией рекурсии.
В том же посте имеется описание фрактальной природы алгоритма. Я попытаюсь продолжить это направление, раскрыв применение кода Грея для данной конкретной задачи.
Приведу цитату из соответствующей статьи в Википедии:
Коды Грея применяются в решении задачи о Ханойских башнях. Пусть N — количество дисков. Начнём с кода Грея длины N, состоящего из одних нулей (то есть G (0)), и будем двигаться по кодам Грея (от G (i) переходить к G (i+1)). Поставим в соответствие каждому I-ому биту текущего кода Грея I-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита I как перемещение I-го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если N нечётно, то последовательность перемещений наименьшего диска имеет вид f→t→r→f→t→r→… (где f-стартовый стержень, t-финальный стержень, r-оставшийся стержень), а если N чётно, то f→r→t→f→r→t→…
Оптимальное решение задачи сводится к определению положения дисков после очередного хода. В самом начале (при нулевом ходе) все диски находятся на одном и том же стартовом стержне f. Нумерация весов дисков осуществляется с номера 1 по возрастанию. Требуется описать положение дисков на ходе с номером m.
Очевидно, что при оптимальном решении после хода m количество перемещаемых дисков n будет не более
(1).
Остальные диски большего размера можно не брать в расчёт, что очень удобно при более общем предположении о бесконечном количестве дисков в начальной задаче с тремя стержнями.
Далее, определившись с количеством перемещенных дисков, определимся с их положением.
Ввиду фрактальности решения, которое описывалось в упомянутых выше источниках, становится очевидным, что благодаря «вложенности» решений друг в друга просматривается связь между двоичным кодом номера хода и номером перемещаемого диска.
В частности, во время данного хода перемещается тот диск, чей «вес» i коррелирует с максимальной степенью двойки в двоичном разложении номера m текущего хода минус единицу: (2).
В той же нотации Pascal/Delphi, которую использует MrShoor в своем коде, это может быть записано следующим образом:
i:=0;
deg2value:=1;
while ((m mod deg2value) = 0)) do
begin
i:=i+1;
deg2value:=deg2value*2;
end;Таким образом, для каждого из дисков с весом i мы можем определить тот ход j, на котором диск данного веса был перемещен последний раз:
.
Код для определения номера хода num_move последнего перемещения диска с весом i может выглядеть подобным образом (с условием включения модуля Math):
deg2value:=Power(2,i-1);
q_move:=m div deg2value;
if (q_move mod 2) = 0 then q_move:=q_move-1;
num_move:=i_move * deg2value;
q_move=(q_move+1) div 2;Стоит обратить внимание на тот факт, что попутно в переменной q_move получено количество перемещений диска с весом i с начала игры.
Итак, в промежуточном итоге, мы знаем, сколько раз каждый диск был перемещен в течение игры после каждого хода. Теперь определимся с тем, куда перемещался каждый из дисков.
Как отмечено в Википедии, перемещение верхнего диска циклично и, при выборе определенного стержня назначения t, если N нечётно, то последовательность перемещений наименьшего диска имеет вид f→t→r→f→t→r→… (где f-стартовый стержень, t-финальный стержень, r-оставшийся стержень), а если N чётно, то f→r→t→f→r→t→…
Вспоминая о фрактальности, можно заметить, что если отбросить верхнюю часть предшествующих дисков, то текущий диск также совершает подобное циклическое движение во время своих собственных ходов. Учитывая этот факт, становится очевидным, что в зависимости от четности номера диска, цикл перемещения нечетного диска совпадает с циклом перемещения первого диска, а цикл перемещения четных дисков разнится очередностью стержней t и r.
В частности, зная количество перемещения q_move и четность номера текущего диска, можно простым делением на 3 по остатку определить последний стержень, куда был перемещен данный диск.
Следовательно, имея на входе общее количество дисков N, выбранный стержень назначения t и номер текущего хода m, можно восстановить положение всех дисков при оптимальном решении без обращения к рекурсивным алгоритмам.
Для тех, кому интересны вариации задачи Ханойских башен, в частности, случаи 4 и более стержней, предлагаю ознакомиться с опытом PapaBubaDiop, развивающего данное направление в виде игр, попутно пытаясь монетизировать некоторые версии на различных платформах.
Надеюсь, что тем из читателей, которым интересны теоретические решения, более оптимизированные для подобных задач с большим количеством входных данных и затрачиваемых вычислительных ресурсов, эта публикация пригодится в дальнейшем в качестве базиса для собственных результатов.
Стиль и язык немного суховаты и годятся скорее для академических работ, потому прошу не судить особо строго, особенно с учетом попытки выправить карму и выбраться из минуса. Всем всего наилучшего и светлого, с Новым 2017 Годом: успехов и удач во всем хорошем!
Комментарии (11)
Sirion
5 января 2017 в 05:34
+1↑
↓
Стиль и язык немного суховаты и годятся скорее для академических работ
Склонен не согласиться. Нельзя назвать суховатым то, что состоит из воды)
maaGames
5 января 2017 в 06:29
+1↑
↓
Но ведь сложность алгоритма не уменьшилась? Вселенной ничего не угрожает?
arsmagic
5 января 2017 в 08:30 (комментарий был изменён)
+1↑
↓
Это всего лишь иллюстрация применения схемы Грея для одной из задач.Для сравнения, попробуйте написать программу с использованием рекурсии, которая просчитывает положение уже хотя бы при перемещении сорокового диска.
Уверен, что вычислительных ресурсов большинства обычных компьютеров не хватит, рекурсивное приложение вылетит по таймауту или из-за нехватки памяти.
А при вышеуказанном подходе достаточно будет сделать около 40 циклов операций пусть с большими, но все еще доступными для машинной обработки обычным ПК числами.
Именно в этом и заключается ценность подобных теоретических оптимизаций.
-
maaGames
5 января 2017 в 08:38
0↑
↓
Как я понимаю, в задаче важно получить результат — перенести башни в соответствии с ограничениями.
Т.е. используя схему Грея можно узнать положение любого из дисков после любого из ходов, но это никак не упрощает задачу по переносу, т.к. количество перемещений дисков остаётся тем же. Т.е. для решения всей задачи всё-равно придётся на каждом ходе вычислять положение каждого диска и мы вернёмся всё к той же квадратичной сложности и «вылету по таймауту».-
arsmagic
5 января 2017 в 08:58 (комментарий был изменён)
+1↑
↓
Отнюдь.
Рекурсивное решение для перемещения сорокового диска как минимум потребует переноса предыдущего диска, что приведет к необходимости совершить
итераций.
В случае же теоретического решения достаточно будет высчитать номер первого хода, при котором будет перемещен 40-й диск —, далее максимальный номер хода для 39-го диска, для 38-го, для 37 и так далее, вплоть до диска 1.
Попутно для каждого из ходов будет получено количество перемещений для каждого из дисков, которое надо будет сводить по модулю 3 к одному из значений стержней f, t или r. Таким образом, будет произведено не более 200 вычислений высокого порядка.
Согласитесь, что порядок числа 200 много меньше порядка числа двойки в 39-й степени.-
maaGames
5 января 2017 в 09:01
0↑
↓
Вы недопоняли. За 200 шагов вы не сможете перенести башню из 40 дисков с первого штыря на третий.-
arsmagic
5 января 2017 в 09:05 (комментарий был изменён)
+1↑
↓
Естественно. Но за 200 шагов я сумею описать положение всех дисков для того хода, когда перенесен 40-й. Что практически недостижимо, если данную же задачу решать рекурсивным способом. Вчитайтесь, пожалуйста, в детали.
-
maaGames
5 января 2017 в 09:10
0↑
↓
Т.е. у вас будет «строка» с описанием перемещений каждого диска на каждом шаге, начиная с самого начала? Вместо 2^40 итераций будет 2^40 записей. Всего 1ТБ. Действительно, нынешним компьютерам уже по силам столько сохранить.-
arsmagic
5 января 2017 в 09:17 (комментарий был изменён)
0↑
↓
Не совсем так. У меня на выходе массив из 40 значений, в котором индекс — это номер диска, а само значение будет f, t или r.
Но даже если даже принимать Вашу интерпретацию, которая чуть уводит в сторону от самого назначения теоретического решения, то тем более получается значительная оптимизация: вместо хранения терабайтов информации предлагается использовать функциональный подход для описания ситуации с перемещениями, что много выгоднее хранения всех данных.
-
maaGames
5 января 2017 в 09:27
+1↑
↓
Ну я об этом и говорю! Задача — перенести башню. Практически, теоретически — не важно. Чтобы перенести всю башню с первого на последний штырь нужно знать абсолютно все перемещения, начиная с исходного положения, поэтому придётся хранить.
А то получается «как нарисовать сову». Вот башня, а вот положение при последнем шаге, когда осталось перенести один диск.
В принципе, всё ожидаемо: либо скорость (коды Грея), либо используемая память (рекурсия).Т.е. если задача не в переносе, а в определении состояния на произвольном шаге, тот схема Грея тут на голову эффективнее, но для полной задачи разницы как бы и нет.
-
arsmagic
5 января 2017 в 09:32
0↑
↓
Конечно))) Тем более, что изначально указывается информация о том, что для оптимального решения с n дисками потребуется
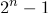ходов.
