[Перевод] В самом популярном фрагменте кода за всю историю StackOverflow ошибка!
Недавнее исследование «Использование и атрибуция сниппетов кода Stack Overflow в проектах GitHub» внезапно обнаружило, что чаще всего в опенсорсных проектах встречается мой ответ, написанный почти десять лет назад. По иронии судьбы, там баг.
Давным-давно…
Еще в 2010 году я сидел в своём офисе и занимался ерундой: развлекался код-гольфингом и накручивал рейтинг на Stack Overflow.
Мой внимание привлёк следующий вопрос: как вывести количество байт в удобочитаемом формате? То есть как преобразовать что-то вроде 123456789 байт в »123,5 МБ».
Старый добрый интерфейс 2010 года, спасибо The Wayback Machine
Неявно подразумевалось, что результатом будет число между 1 и 999,9 с соответствующей единицей измерения.
Уже был один ответ с циклом. Идея простая: проверять все степени с самой большой единицы (ЭБ = 1018 байт) до самой маленькой (Б = 1 байт) и применить первую, которая меньше числа байт. В псевдокоде это выглядит примерно так:
suffixes = [ "EB", "PB", "TB", "GB", "MB", "kB", "B" ]
magnitudes = [ 1018, 1015, 1012, 109, 106, 103, 100 ]
i = 0
while (i < magnitudes.length && magnitudes[i] > byteCount)
i++
printf("%.1f %s", byteCount / magnitudes[i], suffixes[i])
Обычно при наличии правильного ответа с положительной оценкой его трудно догнать. На жаргоне Stack Overflow это называется проблемой самой быстрой пушки на Западе. Но здесь у ответа был несколько недостатков, поэтому я всё равно надеялся его превзойти. По крайней мере, код с циклом можно значительно сократить.
Это ж алгебра, всё просто!
Тут меня осенило. Приставки кило-, мега-, гига-, … — ни что иное, как степени 1000 (или 1024 в стандарте МЭК), так что правильную приставку можно определить с помощью логарифма, а не цикла.
Основываясь на этой идее, я опубликовал следующее:
public static String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
if (bytes < unit) return bytes + " B";
int exp = (int) (Math.log(bytes) / Math.log(unit));
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Конечно, это не очень читабельно, и log/pow уступает по эффективности другим вариантам. Но никакого цикла и почти нет ветвлений, так что результат получился довольно красивым, на мой взгляд.
Математика тут нехитрая. Количество байт выражается как byteCount = 1000s, где s представляет степень (в двоичной нотации база 1024.) Решение s дает s = log1000(byteCount).В API нет простого выражения log1000, но мы можем выразить его в терминах натурального логарифма следующим образом s = log (byteCount) / log (1000). Затем преобразуем s в int, так что если у нас, например, более одного мегабайта (но не полный гигабайт), то в качестве единицы измерения будет использоваться МБ.
Получается, что если s = 1, то используется размерность килобайт, если s = 2 — мегабайт и так далее. Делим byteCount на 1000s и шлёпаем соответствующую букву в префикс.
Оставалось только подождать и посмотреть, как сообщество воспримет ответ. Я подумать не мог, что этот фрагмент кода станет самым тиражирумым в истории Stack Overflow.
Исследование по атрибуции
Перенесёмся в 2018 год. Аспирант Себастьян Балтес публикует в научном журнале Empirical Software Engineering статью под названием «Использование и атрибуция сниппетов кода Stack Overflow в проектах GitHub». Тема его исследования — насколько соблюдается лицензия Stack Overflow CC BY-SA 3.0, то есть указывают ли авторы ссылки на Stack Overflow как источник кода.
Для анализа из дампа Stack Overflow были извлечены сниппеты кода и сопоставлены с кодом в публичных репозиториях GitHub. Цитата из реферата:
Представляем результаты крупномасштабного эмпирического исследования, анализирующего использование и атрибуцию нетривиальных фрагментов кода Java из ответов SO в публичных проектах GitHub (GH).
(Спойлер: нет, большинство программистов не соблюдает требования лицензии).
В статье есть такая таблица:
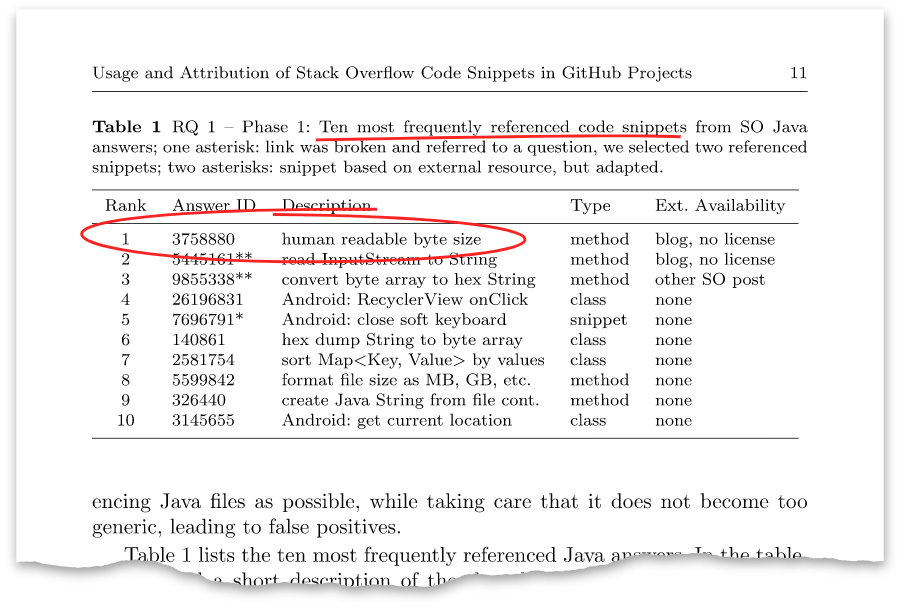
Этот ответ вверху с идентификатором 3758880 оказался тем самым ответом, который я опубликовал восемь лет назад. На данный момент у него более ста тысяч просмотров и более тысячи плюсов.
Быстрый поиск на GitHub действительно выдаёт тысячи репозиториев с кодом humanReadableByteCount.
Поиск этого фрагмента в своём репозитории:
$ git grep humanReadableByteCountЗабавная история, как я узнал об этом исследовании.Себастьян нашёл совпадение в репозитории OpenJDK без какой-либо атрибуции, а лицензия OpenJDK не совместима с CC BY-SA 3.0. В списке рассылки jdk9-dev он спросил: это код Stack Overflow скопирован из OpenJDK или наоборот?
Самое смешное то, что я как раз работал в Oracle, в проекте OpenJDK, поэтому мой бывший коллега и друг написал следующее:
Привет,
Почему бы не спросить напрямую у автора этого сообщения на SO (aioobe)? Он является участником OpenJDK и работал в Oracle, когда этот код появился в исходных репозиториях OpenJDK.
Oracle очень серьёзно относится к таким вопросам. Я знаю, что некоторые менеджеры вздохнули с облегчением, когда прочитали этот ответ и нашли «виновника».
Затем Себастьян написал мне, чтобы прояснить ситуацию, что я и сделал: этот код добавили ещё до моего прихода в Oracle и я не имею отношения к коммиту. С Oracle лучше не шутить. Через пару дней после открытия тикета этот код был удалён.
Баг
Держу пари, вы уже задумались об этом. Что же за ошибка в коде?
Ещё раз:
public static String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
if (bytes < unit) return bytes + " B";
int exp = (int) (Math.log(bytes) / Math.log(unit));
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp-1) + (si ? "" : "i");
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Какие варианты?
После эксабайтов (1018) идут зеттабайты (1021). Может, действительно большое число выйдет за границы kMGTPE? Нет. Максимальное значение 263–1 ≈ 9,2 × 1018, поэтому никакое значение никогда не выйдет за пределы экзабайт.
Может, путаница между единицами СИ и двоичной системой? Нет. В первой версии ответа была путаница, но её исправили довольно быстро.
Может, exp в конечном итоге обнуляется, вызывая сбой charAt (exp-1)? Тоже нет. Первый if-оператор охватывает этот случай. Значение exp всегда будет не менее 1.
Может, какая-то странная ошибка округления в выдаче? Ну вот наконец…
Много девяток
Решение работает до тех пор, пока не приблизится к 1 МБ. Когда в качестве входных данных задано 999 999 байт, результат (в режиме СИ) — "1000,0 kB". Хотя 999 999 ближе к 1000 × 10001, чем к 999,9 × 10001, сигнификант 1000 запрещён спецификацией. Правильный результат — "1.0 MB".
В своё оправдание могу сказать, что на момент написания такая ошибка была во всех 22 опубликованных ответах, включая Apache Commons и библиотеки Android.
Как это исправить? Прежде всего, отметим, что показатель степени (exp) должен измениться с «k» на «M», как только число байт ближе к 1 × 1,0002 (1 МБ), чем к 999,9 × 10001 (999,9 k). Это происходит на 999 950. Точно так же следует переключиться с «M» на «G», когда мы проходим 999 950 000 и так далее.
Вычисляем этот порог и увеличиваем exp, если bytes больше:
if (bytes >= Math.pow(unit, exp) * (unit - 0.05))
exp++;
С этим изменением код работает хорошо до тех пор, пока количество байт не приблизится к 1 ЭБ.
Ещё больше девяток
При расчёте 999 949 999 999 999 999 код выдаёт 1000.0 PB, а правильный результат 999.9 PB. Математически код точен, так что же здесь происходит?
Теперь мы столкнулись с ограничениями double.
Введение в арифметику с плавающей запятой
Согласно спецификации IEEE 754, у близких к нулю значений с плавающей запятой очень плотное представление, а у больших значений — очень разреженное. На самом деле, половина всех значений находится между -1 и 1, а когда речь идёт о больших числах, значение размеромLong.MAX_VALUEничего не значит. В прямом смысле.double l1 = Double.MAX_VALUE; double l2 = l1 - Long.MAX_VALUE; System.err.println(l1 == l2); // prints true
Подробнее см. «Биты значения с плавающей запятой».
Проблему представляют два вычисления:
- Деление в аргументе
String.formatи - Порог для наращивания
exp
Мы можем переключиться на BigDecimal, но это скучно. Кроме того, здесь тоже возникают проблемы, потому что в стандартном API нет логарифма для BigDecimal.
Уменьшение промежуточных значений
Для решения первой проблемы можем уменьшить значение bytes до нужного диапазона, где точность лучше, и соответственно настроить exp. Конечный результат в любом случае округляется, поэтому неважно, что мы выбрасываем наименее значимые разряды.
if (exp > 4) {
bytes /= unit;
exp--;
}Настройка наименее значимых битов
Для решения второй проблемы нам важны наименее значимые биты (у 99994999…9 и 99995000…0 должны быть разные степени), поэтому придётся найти иное решение.
Сначала отметим, что существует 12 различных пороговых значений (по 6 для каждого режима), и только одно из них приводит к ошибке. Неправильный результат можно однозначно идентифицировать, потому что он заканчивается на D0016. Значит, можно исправить его напрямую.
long th = (long) (Math.pow(unit, exp) * (unit - 0.05));
if (exp < 6 && bytes >= th - ((th & 0xFFF) == 0xD00 ? 52 : 0))
exp++;
Поскольку в результатах с плавающей запятой мы полагаемся на определённые битовые шаблоны, то применяем модификатор strictfp для гарантии, что код работает независимо от аппаратного обеспечения.
Отрицательные значения на входе
Неясно, при каких обстоятельствах можем иметь смысл отрицательное количество байт, но поскольку в Java нет беззнакового long, лучше обработать такой вариант. Прямо сейчас ввод вроде -10 000 выдаёт -10000 B.
Напишем absBytes:
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
Выражение такое многословное, потому что -Long.MIN_VALUE == Long.MIN_VALUE. Теперь мы выполняем все вычисления exp, используя absBytes вместо bytes.
Окончательная версия
Вот окончательная версия кода, сокращённая и уплотнённая в духе оригинальной версии:
// From: https://programming.guide/the-worlds-most-copied-so-snippet.html
public static strictfp String humanReadableByteCount(long bytes, boolean si) {
int unit = si ? 1000 : 1024;
long absBytes = bytes == Long.MIN_VALUE ? Long.MAX_VALUE : Math.abs(bytes);
if (absBytes < unit) return bytes + " B";
int exp = (int) (Math.log(absBytes) / Math.log(unit));
long th = (long) (Math.pow(unit, exp) * (unit - 0.05));
if (exp < 6 && absBytes >= th - ((th & 0xfff) == 0xd00 ? 52 : 0)) exp++;
String pre = (si ? "kMGTPE" : "KMGTPE").charAt(exp - 1) + (si ? "" : "i");
if (exp > 4) {
bytes /= unit;
exp -= 1;
}
return String.format("%.1f %sB", bytes / Math.pow(unit, exp), pre);
}
Обратите внимание, что это началось как попытка избежать циклов и чрезмерного ветвления. Но после сглаживания всех пограничных ситуаций код стал ещё менее читабельным, чем исходная версия. Лично я бы не стал копировать этот фрагмент в продакшн.
Для обновлённой версии продакншн-качества см. отдельную статью: «Форматирование размера байт в удобочитаемый формат».
Ключевые выводы
- В ответах на Stack Overflow могут быть ошибки, даже если у них тысячи плюсиков.
- Проверьте все граничные случаи, особенно в коде со Stack Overflow.
- Арифметика с плавающей запятой сложна.
- Обязательно указывайте правильную атрибуцию при копировании кода. Кто-то может вывести вас на чистую воду.
