[Перевод] Ускоренный курс по нотациям в теории языков программирования06.08.2015 15:48

Программисты часто сталкиваются с проблемами чтения математических нотаций, когда пытаются разобраться с теоретическими основами какого-либо языка программирования. Также с ними толкнулся и я в своих теоретических изысканиях. К счастью, мне очень помогла замечательная статья Джереми Сиека (Jeremy Siek), чьим переводом я хочу с вами поделиться. Надеюсь она поможет многим программистам-«не математикам».

Вступление

Этим постом я хочу помочь моим друзьям с чтением других моих постов. Это ускоренный курс по нотациям, используемым в теории языков программирования (ТЯП). Для гораздо лучшего изучения темы я рекомендую «Types and Programming Languages» от Benjamin C. Pierce и «Semantic Engineering with PLT Redex» от Felleisen, Findler, and Flatt. Я предполагаю, что читатель опытный программист, но не так хорош в математике и ТЯП. Я начну с базовых определений и попытаюсь быстро ввести вас в курс дела.

Множества, кортежи, отношения и определения правилами

Я подозреваю, что многие читатели будут знакомы с множествами, кортежами и отношениями, но если вы не знакомы с индуктивными определениями, тогда прочитайте секцию ниже «определение правилами».

Множества

Основной строительный блок, который мы используем в ТЯП — это множество, т.е. коллекция объектов (или элементов). Например множество, состоящее из первых трех натуральных чисел: {0, 1, 2}.
Единственный факт, имеющий значение, это принадлежит ли объект множеству или нет. Не важно, есть ли дубликаты или какой порядок появления объекта в множестве. Например множество {0, 2, 1}, тоже же самое множество, что и приведенное сверху. Нотация ∈ означает «в». Таким образом 1 ∈ {0, 1, 2} истина и 3 ∈ {0, 1, 2} ложь. Множества могут содержать бесконечное количество элементов. Например множество всех натуральных чисел (неотрицательных целых), обозначаемое N.

Кортежи

Другой строительный блок — это кортеж, т.е. упорядоченная коллекция объектов. Т.о. (0, 1, 2) является кортежем из трех элементов и он отличается от кортежа (0, 2, 1). Подстрочая нотация ti означает i-й (с индексом i) элемент кортежа t. Например, если t = (0, 2, 1), тогда t1 = 0, t2 = 2, t3 = 1. Кортежи всегда содержат конечное количество элементов и обычно достаточно немного. Иногда для обозначения кортежей используются угловые скобки вместо круглых: .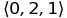

Отношения

Комбинируя кортежи и множества мы получаем отношения. Отношение — это множество кортежей.

{(0, 1), (1,2), (2, 3), (3, 4), …}

Мы часто используем отношения для отображения входных значений на выходные. Например, мы можем думать об отношении выше как о отображении натурального числа на его последователя, т.е. на следующее большее натуральное число. Определение сверху достаточно неточное из-за использования (…). К счастью, есть более точные нотации для описания бесконечных множеств и отношений.

Определение правилами

Основной способ, которым мы определяем бесконечные множества в ТЯП — предоставляем набор правил, описывающих, какие элементы входят в множество. Давайте используем имя R для множества сверху. Тогда два следующих правила дадут нам точное определение R. Обратите внимание, что второе правило рекурсивное в том смысле, что ссылается на само себя. Это нормальная и достаточно распространенная ситуация.

(0, 1) ∈ R.
Для любых натуральных чисел n и m, если (n, m) ∈ R, то (n + 1, m + 1) ∈ R.

Когда мы используем правила для определения множества, мы подразумеваем, что элемент не входит в множество, если нет способа использовать данные правила, чтобы оправдать нахождение этого элемента в множестве. Так (0, 0) не входит в R, потому что с помощью указанных правил нельзя обосновать, что (0, 0) туда входит.
Некоторые наборы правил бессмысленны и не определяют множество. Например, правила не должны противоречить друг другу, как здесь:

(0, 1) ∈ R.
(0, 1) ∉ R.

Учебник по ТЯП описывает ограничения для «хороших» наборов правил, но мы не будем в это углубляться. Скажем только, что хотя бы одно правило должно быть нерекурсывным и подобные логические противоречия должны отсутствовать.
Общераспространенная нотация для правил, как выше, использует горизонтальную черту между «if» и «then». Например, эквивалентное определение для R дается следующим образом.

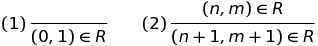
$(1)\,\frac{}{(0,1) \in R}\qquad(2)\,\frac{(n,m) \in R}{(n+1,m+1) \in R}$

Мы опустили «для любых натуральных чисел n и m» из правила 2. Используется соглашение, согласно которому переменные, такие как n и m, которые появляются в правиле, могут быть заменены любым объектом корректного типа. В данном случае натуральным числом. Часто, «корректный тип», это что-то о чем можно догадаться из контекста беседы. В данном случае — натуральные числа.
Предположим, я утверждаю, что некоторый элемент входит в R. Скажем, (2, 3) ∈ R. Вы можете ответить, что не верите мне. Чтобы вас убедить, мне нужно показать, как правила оправдывают, тот факт, что (2, 3) ∈ R. Я должен показать вам вывод. Вывод — это цепочка правил, в которой переменные, такие как n и m, заменяются конкретными значениями и предпосылки, такие как (n, m) ∈ R, заменяются более конкретными выводами.

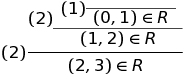
$(2)\frac{ (2)\begin{array}{c} (1)\begin{array}{c} \\\hline (0,1) \in R\end{array} \\\hline (1,2) \in R \end{array}}{ (2,3) \in R}$

Я пометил каждый шаг в выводе номером правила. Причудливое название для того, что я называю «определение правилами» — индуктивное определение.

Синтаксис языка и грамматики

Оказывается, что использование правил для определения множеств, как мы делали выше, подходит и для определения синтаксиса языка программирования. Предположим, что нам нужно определить простой язык для целочисленной арифметики. Назовем его Arith. Он будет содержать выражения, такие как 1 + 3 и -(5 + 2). Вспомним, что Z — множество целых чисел. Тогда множество правил, описывающих Arith, будет таким:

Для любого i ∈ Z верно, что i ∈ Arith.
Для любого e, если e ∈ Arith, тогда -e ∈ Arith.
Для любого e1 и e2, если e1 ∈ Arith и e2 ∈ Arith, тогда e1 + e2 ∈ Arith.
Для любого e, если e ∈ Arith, тогда (e) ∈ Arith.

Бэкуса-Наура форма (БНФ) — другая распространенная нотация для записи правил, определяющих синтаксис языка, которая означает тоже самое. (Существует несколько вариантов БНФ. Я забыл, какую именно использую здесь.) Набор правил называется грамматикой.

Arith ::= integer
Arith ::= "-" Arith
Arith ::= Arith "+" Arith
Arith ::= "(" Arith ")"

Вертикальная черта (означающая «или») часто используется для того, чтобы сделать синтаксис более кратким.

Arith::= integer | »-» Arith | Arith »+» Arith | »(» Arith »)»

В ТЯП мы используем своеобразный вариант БНФ, который заменяет имя определяемого языка, в данном случае Arith, на переменную, которая используется для прохода по элементам Arith. Теперь предположим, что используем переменную i как заполнитель (placeholder) для целых чисел и e как заполнитель для элементов Arith. Тогда мы можем записать нашу грамматику так:

e ::= i ∣ −e ∣ e + e

Обратите внимание, что я опустил скобки. Как правило понятно, что скобки разрешены в любом языке. Понятие вывода совпадает с деревом разбора (parse tree). Они оба демонстрируют, почему конкретный элемент входит в множество.

Операционная семантика

Описать язык, значит описать, что произойдет при запуске программы на этом языке. Именно это делает операционная семантика. В случае с Arith нам нужно указать целочисленный результат для каждой программы. Как было сказано выше, мы можем использовать отношения для отображения входных данных на результат. И обычно мы так и делаем в ТЯП. Есть несколько различных стилей отношений. Первый, который мы рассмотрим, это семантика большого шага (big-step semantics), которая отображает программу прямо на её результат.

Семантика большого шага (big-step semantics)

Определим отношение Eval, которое отображает элементы Arith на целые числа. Например, должно выполняться условие (−(2 + −5), 3) ∈ Eval. Это отношение будет бесконечным (потому что существует бесконечное количество программ на Arith). И снова мы будем использовать набор правил для определения Eval. Но перед тем как мы начнем, введем сокращение: e ⇓ i означает (e, i) ∈ Eval. Ниже мы опишем правила, определяющие Eval с использованием нотации с горизонтальной чертой. Чтобы убедиться, что не пропустим ни одной программы, создадим одно правило для каждого синтаксического правила Arith (их три). Будем говорить, что правила синтаксически-ориентированные, когда одно правило соответствует каждому синтаксическому правилу языка.

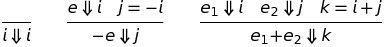
$\frac{}{i \Downarrow i}\qquad\frac{e \Downarrow i \quad j = -i}{\mathtt{-}e \Downarrow j}\qquad\frac{e_1 \Downarrow i \quad e_2 \Downarrow j \quad k = i + j} {e_1\mathtt{+}e_2 \Downarrow k}$

Это может показаться немного странным, что я определил »-» в терминах »-» и »+» в терминах »+». Не циклическая ли это зависимость? Ответ — нет. Плюс и минус — это обычные арифметические операции для целых чисел, которые каждый проходит в школе. В этом смысле более странным для Arith было бы не использовать 32 или 64-битную арифметику. Программист, реализующий Arith, мог бы использовать пакет для работы с BigInteger, чтобы обрабатывать арифметику.

Семантика малого шага (small-step semantics)

Второй и наиболее распространенный стиль операционной семантики — это семантика малого шага. В этом стиле отношение не отображает программу на её результат. Вместо этого оно отображает программу на слегка упрощенную программу, в которой какое-то подвыражение заменяется его результатом. Можно думать об этом стиле, как о текстовой замене. Чтобы дать пример этого стиля, определим отношение Step. Это отношение будет содержать следующие элементы, как и многие другие:

(-(2 + -5), -(-3)) ∈ Step
        (-(-3), 3) ∈ Step

Снова введем сокращение: e1 ⟶ e2 означает (e1, e2) ∈ Step. И если мы соединим шаги вместе, то e1 ⟶ e2 ⟶ e3 будет означать e1 ⟶ e2 и e2 ⟶ e3. Синонимом для шага (step) будет термин «сократить» (reduce). Предыдущий пример из двух шагов может быть записан теперь так:

-(2 + -5) ⟶ -(-3) ⟶ 3

Теперь перейдем к правилам, определяющим отношение Step. Здесь пять правил, которые мы объясним ниже.

$\begin{gather*} (1)\frac{j = -i}{\mathtt{-}i \longrightarrow j} \qquad (2)\frac{k = i + j}{i \mathtt{+} j \longrightarrow k} \\[3ex] (3)\frac{e \longrightarrow e'}{\mathtt{-}e \longrightarrow \mathtt{-}e'} \qquad (4)\frac{e_1 \longrightarrow e'_1}{ e_1 \mathtt{+} e_2 \longrightarrow e'_1 \mathtt{+} e_2} \qquad (5)\frac{e_2 \longrightarrow e'_2}{ i \mathtt{+} e_2 \longrightarrow i \mathtt{+} e'_2} \end{gather*}$

Правила (1) и (2) наиболее интересные. Они выполняют арифметику. Мы называем их «вычислительные правила сокращения» (computational reduction rules). Правила (3–5) позволяют нам заходить в подвыражения для выполнения вычислений. Они часто называются правилами соответствия (congruence rules) по причинам в которые мы сейчас не будем вдаваться. Использование переменной i в правиле (5) означает, что сокращение происходит слева направо. В частности, мы не позволяем сокращать правое выражение от знака + до тех пор, пока левое выражение не будет сокращено до целого числа.

Отступление: Рассматриваемый здесь порядок «слева направо» я выбрал как дизайнер языка. Я мог бы не определять порядок, позволяя быть ему неопределенным. Наш язык не имеет побочных эффектов, поэтому порядок не имеет значения. Однако, большинство языков имеют побочные эффекты и они определяют порядок (но не все), поэтому я подумал, что нужно рассмотреть пример того, как обычно определяет порядок.

Время для примера. Посмотрим на вывод для шага:

-(2 + -5) ⟶ -(-3).

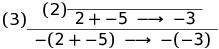
$(3)\begin{array}{c} (2)\begin{array}{c}\\\hline \mathtt{2 + -5} \;\longrightarrow\; \mathtt{-3} \end{array} \\\hline\mathtt{-(2 + -5)}\;\longrightarrow\; \mathtt{-(-3)}\end{array}$

Мы определили один шаг вычислений, т.е. отношения Step. Но мы не совсем закончили. Мы ещё должны определить, что значит выполнить программу до завершения. Мы сделаем это с помощью определения Eval' в терминах отношения Step. Иными словами, отношение Eval' будет содержать любые пары (e, i) если выражение e сокращается до целого i за ноль или более шагов. Здесь присутствует новая нотация, которая объясняется далее.

Eval′ = {(e, i) ∣ e ⟶∗ i}

Нотация {…∣…} определяет конструктор множества. Выражение слева от вертикальной черты определяет шаблон для типичного элемента множества и выражение справа — ограничения на элементы множества. Нотация ⟶∗ означает ноль или более шагов. Я бы определил эти многошаговые отношения с помощью правил:

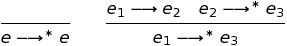
$\frac{}{e \longrightarrow^{*} e}\qquad\frac{e_1 \longrightarrow e_2 \quad e_2 \longrightarrow^{*} e_3} {e_1 \longrightarrow^{*} e_3}$

(Я думаю об этом в терминах Lisp-подобных списков. Так, первому правилу соответствует nil, а второму cons.)

Системы типов (с лямбда-исчислением в качестве примера)

Многие языки программирования статически типизированы, т.е. компилятор выполняет некоторые проверки корректности прежде, чем выполнить реальную компиляцию. Обычно, во время проверки компилятор убеждается в том, что объекты используются так, как должны. Например, что никто не пытается использовать целое число как функцию. Способ, которым разработчик языка указывает какие именно проверки должны быть выполнены, является определение системы типов для языка. Язык Arith настолько прост, что в нем нет никаких интересных проверок типов. Рассмотрим более сложный язык, который снова и снова используется в ТЯП — лямбда-исчисление (технически, лямбда-исчисление с упрощенной типизацией). Лямбда-исчисление состоит только из анонимных функций. Мы же расширим лямбда-исчисление так, чтобы оно включало наши арифметические выражения. Тогда наш язык будет определяться следующей грамматикой.

e ::= i ∣ −e ∣ e + e ∣ x ∣ e e ∣ λx:T.e

Переменная x перечисляет имена параметров, такие как foo и g. Следующие справа два выражения (e e) означают применение функции (или вызов функции). Если вы знакомы с языком C, можете читать e1 e2 как e1(e2). В лямбда-исчислении функции принимают только один параметр, поэтому вызов функции требует только один аргумент. Синтаксис λx: T.e создает функцию с одним параметром x типа T (типы мы скоро определим) и телом, состоящим из выражения e. (Часто люди заблуждаются думая, что x — это имя функции. На самом деле это имя параметра, т.к. функции являются анонимными, т.е. не имеют имени.) Возвращаемым значением функции будет результат выражения e. Теперь подумаем о том, какие объекты будут существовать во время выполнения программы. Это целые числа и функции. Мы создадим множество типов для описания сортов объектов, используя T для перечисления множества типов.

T ::= Int ∣ T → T

В функциональном типе T1 → T2, T1 является типом параметра, а T2 типом возвращаемого значения.
Работа системы типов заключается в том, чтобы прогнозировать, какой тип значения будет у результата выражения. Например, выражение -(5 + 2) должно иметь тип Int, потому что результат -(5 + 2) — это число -3, которое является целым. Также как в случае определения синтаксиса или операционной семантики языка, ТЯП-теоретик использует отношения и правила для определения системы типов. Мы определим отношение WellTyped, которое, в первом приближении, отображает выражения на типы. Например, будет выполнено (-(5 + 2), Int) ∈ WellTyped.
Однако, т.к. лямбда-исчисление включает переменные, мы нуждаемся в неком аналоге таблицы символов, отношении, называемом окружением типов (type environment), для отслеживания какие переменные имеют какой тип. Греческая буква Γ (гамма) обычно используется для этой цели. Мы должны быть способны создать новое окружение типов из старого, с возможностью скрывать переменные из внешних областей видимости. Чтобы определить математический аппарат для этих возможностей, положим, что Γ∖x будет отношением, таким же как Γ, за исключением того, что любой кортеж, начинающийся с x будет исключен. (В зависимости от способа, каким будет определена система типов, может быть 0 или 1 кортеж, который начинается с x, делая окружение типов специальным видом отношения, называемого частичная функция (partial function).) Мы будем писать Γ, x: T для операции расширения окружения типов с помощью переменной x, возможно, переопределяющей предыдущее определение, и определяемой следующим образом:

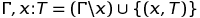
$\Gamma,x{:}T = (\Gamma \backslash x) \cup \{ (x, T) \}$

Предположим, что

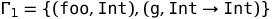
$\Gamma_1 = \{ (\mathtt{foo},\mathtt{Int}), (\mathtt{g},\mathtt{Int} \to \mathtt{Int}) \}$

Тогда

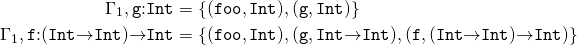
$\begin{align*} \Gamma_1,\mathtt{g}{:}\mathtt{Int} &= \{ (\mathtt{foo},\mathtt{Int}), (\mathtt{g},\mathtt{Int}) \} \ \Gamma_1,\mathtt{f}{:}(\mathtt{Int}{\to}\mathtt{Int}){\to}\mathtt{Int} &= \{ (\mathtt{foo},\mathtt{Int}), (\mathtt{g},\mathtt{Int} {\to} \mathtt{Int}), (\mathtt{f}, (\mathtt{Int}{\to}\mathtt{Int}){\to}\mathtt{Int}) \} \end{align*}$

Окружение типов отличается от глобальной таблицы символов в компиляторе тем, что может существовать более одного окружения типов, по одному для каждой области видимости. Кроме того, мы не обновляем окружение типов, вместо этого мы создаем новое окружение, которое слегка отличается от старого. С точки зрения программирования, математический метаязык, который мы здесь используем, является чистым функциональным (pure functional), т.е. он не содержит побочных эффектов. Читатель может беспокоится о том, что это ведет к неэффективности, но вспомните, что мы не пишем здесь программу, мы пишем спецификацию! Наибольшее значение для нас имеет понятность. И оставаясь чистыми мы можем писать более понятные вещи.
Возвращаясь к отношению WellTyped, вместо того, чтобы содержать кортежи из двух элементов (2-кортежи, пары) оно будет содержать кортежи из трех элементов (3-кортежи, тройки) вида (Γ, e, T). Таким образом мы будем приписывать типы выражениям в контексте окружения типов. Введем ещё одно сокращение (ТЯП-теоретики любят сокращения!). Будем писать Γ ⊢ e: T вместо (Γ, e, T) ∈ WellTyped. Теперь мы готовы перечислить правила, определяющие WellTyped.

$\begin{gather*} \frac{}{\Gamma \vdash i : \mathtt{Int}} \qquad \frac{\Gamma \vdash e : \mathtt{Int}} {\Gamma \vdash \mathtt{-}e : \mathtt{Int}} \qquad \frac{\Gamma \vdash e_1 : \mathtt{Int} \quad \Gamma \vdash e_2 : \mathtt{Int}} {\Gamma \vdash e_1\mathtt{+}e_2 : \mathtt{Int}} \\[3ex] \frac{(x, T) \in \Gamma}{\Gamma \vdash x : T} \qquad \frac{\Gamma,x{:}T_1 \vdash e : T_2 }{\Gamma \vdash (\lambda x{:}T_1. e) : (T_1 \to T_2)} \qquad \frac{\Gamma \vdash e_1 : T \to T' \quad \Gamma \vdash e_2 : T} {\Gamma \vdash e_1 \, e_2 : T'} \end{gather*}$

Подведем итог для правил выше. Арифметические операторы работают с целыми числами. Переменные получают свои типы из окружения. Лямбды являются функциональными типами основанными на типе их параметра и выводимом типе результата. Тело лямбды проверено с использованием окружения из точки создания (lexical scoping), расширенного с помощью параметра этой лямбды. И применение функции не нарушает логики языка до тех пор, пока тип аргумента совпадает с типом параметра.

Заключение

На этом заканчивается этот ускоренный курс по нотациям, используемым в теории языков программирования. Этот пост только описывает основы, но очень много дополнительных нотаций, которые вам понадобятся, являются вариациями рассмотренных здесь. Счастливого чтения и не стесняйтесь задавать вопросы в комментариях.