[Перевод] Улучшенная эвристика при квантовании цветовой палитры
В 2015 году я написал статью о том, как было улучшено квантование цветовой палитры в FFmpeg для создания красивых анимированных гифок. По какой-то причине эта статья — по сей день самая популярная из всех моих постов.
Время шло, я набирал опыт в работе с цветами — и в результате стал весьма стыдиться и переживать по поводу того, в каком состоянии лежат мои фильтры. Многий код в них был наивен (а то и ужасно неправилен), несмотря на всю очевидную результативность этих фильтров.
Вот в чём заключалось одно крупное изменение, которое я хотел внести: оценить расстояния между цветами, воспользовавшись при этом равномерно воспринимаемым цветовым пространством, а не наивное евклидово расстояние между RGB-тройками.
Как обычно, казалось, что с таким проектом можно управиться за неделю. В конце концов, мне всего-то и требовалось изменить функцию расстояния, так, чтобы она стала работать в ином пространстве, верно? Что ж, как обычно, я сам себе устроил множество приключений, наслоившихся друг на друга:
Когда, наконец, удалось дойти до готовности переключиться на OkLab (воспринимаемое цветовое пространство), всего несколько экспериментов показали, что та разновидность ключевого алгоритма, которой я пользовался, содержала несколько изъянов — или, как минимум, в этом алгоритме реализовывалась неоптимальная эвристика. И снова как обычно: вскоре я обнаружил, что уже ввязался в новое исследование, силясь понять, как правильно располагать пиксели на экране. Ниже я изложу историю об ещё одной порции мытарств, которые сам навлёк на свою голову.
Квантование палитры
Но что же такое квантование палитры? В сущности, под этим понимается процесс, при котором количество доступных в изображении цветов сокращается до меньшего подмножества. В sRGB изображение может содержать до 16,7 миллионов цветов. Но на практике цветов гораздо меньше, что, конечно, никого не удивляет. Тем не менее, нередки ситуации, в которых на одной картинке может быть несколько сотен тысяч оттенков. Наша цель — сократить это количество примерно до 256 цветов, наилучшим образом представляющих изображение, а затем, воспользовавшись этими цветами, создать новую картинку.
Зачем? — могли бы спросить вы. На то есть множество причин, вот некоторые из них:
Оптимизировать степень сжатия (естественно, такая операция чревата потерями, и, если сверху заполировать её сглаживанием, тем самым можно погубить весь изначальный замысел)
Некоторые кодеки могут не поддерживать ничего сверх ограниченных палитр (примеры такого рода — GIF или кодеки для субтитров)
Из различных художественных соображений
Ниже приведён пример, в котором картинка квантована на разных уровнях:
оригинал (26125 цветов) | квантована до 8bpp (256 цветов) | квантована до 2bpp (4 цвета) |

Такой процесс квантования цветов можно примерно обобщить в виде четырёхшаговой процедуры:
Сэмплировать входное изображение: строим гистограмму всех цветов, имеющихся на картинке (как правило, дело сводится к простому статистическому анализу).
Проектируем карту цветов: различными способами собираем палитру, пользуясь имеющимися гистограммами
Создаём отображения пикселей, при этом соотносим цвет (который можно найти на входном изображении) с другим цветом (присутствующим в новоиспечённой палитре)
Квантование изображения: на основе полученного отображения цветов строим новое изображения. На данном этапе также может выполняться определённое сглаживание.
В данном исследовании мы сосредоточимся на шаге 2 (который, в свою очередь, базируется на шаге 1).
Алгоритмы проектирования цветовых карт
Палитра — это просто набор цветов. Её можно представить различными способами — например, ниже она показана в 2D и 3D:
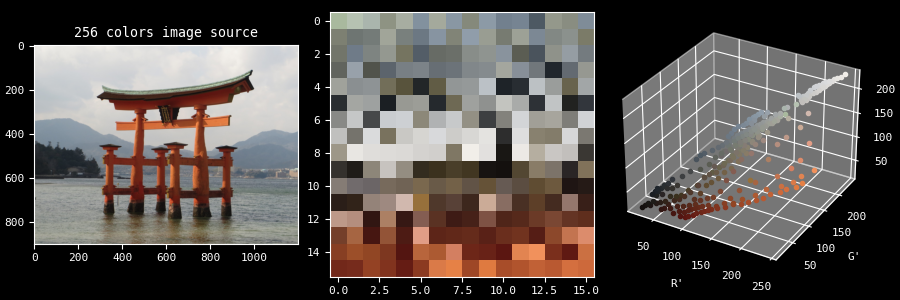
Существуют всевозможные алгоритмы для генерации подобной палитры. Обычно они подразделяются на 2 большие категории:
Алгоритмы разделения/сегментирования (например, деление по среднему (Median-Cut) и его разнообразные разновидности)
Алгоритмы кластеризации (например, K-средние, maximin-расстояние, (E)LBG или попарная кластеризация)
Алгоритмы из первой категории более быстрые, но неоптимальные; алгоритмы из второй категории — медленнее, но лучше. Данная задача является NP-полной; это означает, что для неё возможно найти оптимальное решение, но оно может оказаться крайне дорогостоящим. С другой стороны, можно находить «локальные оптимумы», обходясь минимальными издержками.
Поскольку я работаю в рамках FFmpeg, скорость всегда была для меня приоритетна. Именно поэтому я сразу решил реализовать деление по среднему, предпочтя его более дорогостоящему алгоритму.
В общих чертах этот алгоритм достаточно прост для понимания. Допустим, нам нужна палитра из K цветов. Тогда:
Составляется множество S всех цветов, присутствующих во входной картинке, вместе с соответствующим множеством W весов каждого из цветов (в какой степени они представлены)
Поскольку цвета выражаются в форме RGB-троек, все они могут быть инкапсулированы в большой кубоид (клетку)
Эта клетка разрезается надвое по одной из осей (R, G или B) по медиане (отсюда и англоязычное название алгоритма — Median Cut)
Если у нас ещё нет клеточек в количестве K, то выбираем одну из клеточек и возвращаемся к предыдущему шагу
Затем все цвета в каждой из K клеточек усредняются, образуя компоненты цветовой палитры
Вот как этот процесс выглядит визуально:
Алгоритм деления по середине, нацеленный на 16 клеточек
Возможно, вы заметили, что в вышеприведённом видео цвета выражены не в RGB, а в Lab. Дело в том, что мы не представляем оттенки в цветовом пространстве RGB, а вместо этого пользуемся цветовым пространством OkLab, которое является равномерно воспринимаемым. Алгоритм разделения по среднему, в сущности, не меняется, но в результирующей палитре разница, определённо, видна.
Один из поразительных лимитирующих факторов этого алгоритма заключается в том, что он применим исключительно с кубоидами: разрез можно производить только по оси. Мы не можем сделать сечения по произвольной плоскости или вырезать более сложную фигуру. Представьте, что в данном случае вы работаете с вокселями, а не с более произвольными геометриями. Основное достоинство данного алгоритма в том, что он весьма прост в реализации.
В описании, представленном выше, аккуратно обойдены два важных аспекта, имеющих место на этапах 3 и 4:
Как мы выбираем следующую клеточку, которую собираемся разделить?
Как мы выбираем, по какой оси будем делать разрез клеточки?
Я достаточно долго об этом размышлял.
Обзор возможных вариантов эвристики
В целом, вот те варианты эвристики, которые я пытался обдумывать:
Следует ли выбирать ту клеточку, которая обладает самой длинной осью из всех имеющихся?
Следует ли выбирать клеточку, обладающую максимальным объёмом?
Следует ли выбирать клеточку, для которой характерна наибольшая среднеквадратичная ошибка по сравнению с её средним цветом?
Следует ли выбирать ту клеточку, для оси которой характерна наибольшая СКО?
Предположив, что мы собираемся далее ориентироваться на СКО, должна ли она быть нормализована по всем клеточкам?
Кстати, должны ли мы учитывать вес каждого цвета, либо считать все цвета равными?
Что насчёт оси? Лучше выбрать самую длинную или ту, СКО которой наиболее велика?
Я попытался математически формализовать эти вопросы в меру моих скромных сил. Для начала давайте постулируем, что все цвета c конкретной клеточки хранятся в двумерном массиве N×M, соответствующем следующей матричной нотации:
L₁ | L₂ | L₃ | … | Lₘ |
a₁ | a₂ | a₃ | … | aₘ |
b₁ | b₂ | b₃ | … | bₘ |
N — это количество компонентов (в нашем случае — 3, при работе как с RGB, так и с Lab), а M — это количество цветов в данной клеточке. Можно визуализировать эту структуру и как список векторов, где c_{i, j} — это цвет, расположенный в строке i и столбце j.
Держа это в уме, можно набросать следующую схему, в которой представлено дерево эвристических возможностей, что нам предстоит реализовать:
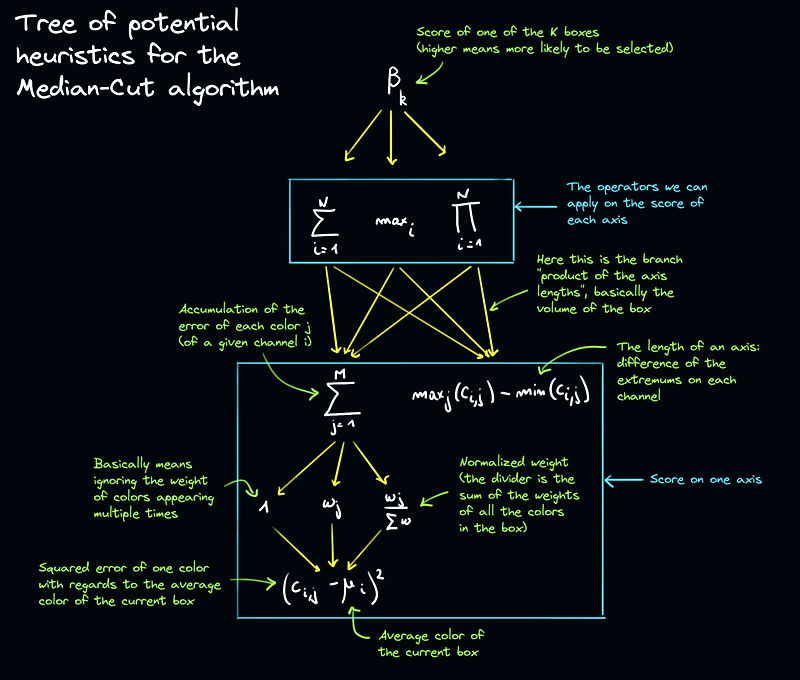
Математики меня просто убьют за то, что вся эта совершенно понятная им символьная китайская грамота пересыпана моими пояснительными заметками, но я считаю эти каракули необходимыми — ведь статью будут читать и простые смертные.
В целом у нас вырисовывается всего 24 комбинации, которые нужно попробовать:
Если попытаться интуитивно поразмыслить, какие из этих метрик покажут себя на практике лучше всего, то быстро приходим к выводу: мы, оказывается, не формализовали, чего именно хотим достичь. Такая корявая ошибка. Как только проясним этот момент — сразу станем точнее представлять, каков может быть вероятный результат.
Я решил нацелиться на такой результат, при котором СКО минимизируется относительно эталонного изображения (с точки зрения восприятия). Иными словами, попытался минимизировать (насколько это возможно) воспринимаемое расстояние между входным и выходным цветным пикселем. Эта цель выбрана произвольно и небесспорна, но она относительно проста и объективна, чтобы с её помощью оценить, вызывает ли у нас доверие выбранная нами модель восприятия. Могла бы быть приемлема и такая метрика: при помощи другого алгоритма выбрать идеальную палитру, а затем сравнивать наш результат именно с ней. К сожалению, последнее подразумевало бы, что мне придётся доверять другому алгоритму, его реализации, а также что у меня хватит на всё это вычислительной мощности.
Итак, резюмируем: я хочу минимизировать СКО между вводом и выводом, если оценка производится в пространстве цветов OkLab. Эту операцию можно выразить следующей формулой:
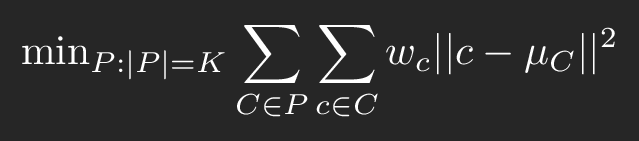
Где:
P — это сегмент (который в нашей реализации ограничивается одной клеточкой)
C — это набор цветов в сегменте P
w — вес цвета
c — отдельно взятый цвет
µ — средний цвет множества C
Особая благодарность criver за неоценимую помощь по части математики, последняя формула взята от них.
Глядя на эту формулу, можно заметить, насколько схоже она выглядит в определённых ветвях эвристического дерева — поэтому, уже можем начинать догадываться о том, каков будет результат эксперимента.
Язык для подготовки эксперимента
Небольшое лирическое отступление от основной темы (если хотите — можете просто пропустить этот раздел и переходить к следующему). Работа с C в FFmpeg быстро превратилась в помеху страшнее всех прочих. Даже не говоря о полной негибкости, неявные приведения предательски портили точность. Ещё несколько раз приходилось сталкиваться с неопределёнными поведениями и всевозможными причудами C, из-за которых не раз довелось усомниться, в уме ли я. Например, следующий код серьёзно меня запутал, когда я пытался с его помощью усреднять цвета:
#include
#include
int main (void)
{
const int32_t x = -30;
const uint32_t y = 10;
const uint32_t a = 30;
const int32_t b = -10;
printf("%d×%u=%d\n", x, y, x * y);
printf("%u×%d=%d\n", a, b, a * b);
printf("%d/%u=%d\n", x, y, x / y);
printf("%u/%d=%d\n", a, b, a / b);
return 0;
}
% cc -Wall -Wextra -fsanitize=undefined test.c -o test && ./test
-30×10=-300
30×-10=-300
-30/10=429496726
30/-10=0 Как бы то ни было, понимаю, что это очевидно — но, если вы ещё не взялись за дело, то рекомендую вам проводить эксперименты на каком-нибудь другом языке (Python или другом), а уже потом переписывать на C — когда вы разберётесь, какого именно результата ожидаете.
Мне не потребовалось много времени, чтобы повторно реализовать на Python всё, что мне требовалось. Версия на Python очевидно исполнялась гораздо медленнее, но это нормально. Оставался достаточный простор для ускорения кода — обычно для этого требуется прибегать к возможностям numpy (с чем мне не захотелось возиться).
Результаты эксперимента
Для описанного проекта я создал исследовательский репозиторий. Сам код, который нужно воспроизвести, а также результаты эксперимента, выложены по адресу color quantization README.
Если коротко — опираясь на результаты, можно прийти к следующим выводам:
В целом, та клеточка, ось которой обладает максимальной ненормализованной взвешенной суммой квадратичной ошибки лучше всего подходит для использования с алгоритмом выбора клеточки.
В целом, наилучшим разрезом оси (в соответствии с алгоритмом выбора) является тот, для которого наблюдается наибольшая взвешенная сумма квадратичной ошибки.
Как ни удивительно, нормализовать веса «поклеточно» — не лучшая идея. Изначально я пришёл к этому выводу методом проб и ошибок, что и стало для меня одним из основных стимулов взяться за это исследование. Сначала я думал, что необходимо нормализовать каждую клеточку, чтобы можно было сравнивать их друг с другом (так сказать, подобрать для их сравнения общий знаменатель). Вот как я в общих чертах смог объяснить этот феномен: если не применять нормализацию, то возникает перекос в сторону сравнительно многоцветных клеточек, но ведь именно к этому мы и стремимся. Полагаю, это также можно объяснить и при помощи нашей оценочной функции: мы хотим минимизировать ошибку в пределах всего набора цветов, так что необходимо, чтобы мелкие (цветовые) сегменты не должны чрезмерно усиливаться. Как минимум, не в контексте поставленной нами цели.
Также интересно обратить внимание вот на что: по-видимому, max() работает лучше, чем sum() вариативности каждого из компонентов. Признаться, моё множество-выборка с картинок получилось не столь большим, и это может означать, что для уверенного подтверждения тенденции потребуются дополнительные эксперименты.
В ретроспективе кажется, что для любого человека с математическим бэкграундом весьма предсказуема. Но, поскольку я не математик, а также не слишком доверяю абстрактному мышлению, я, скажем так, зачастую вынужден пробовать вещи на практике. Вероятно, это один из тех случаев, когда я трачу слишком много сил на что-то изначально очевидное. Но, надеюсь, этот мой рассказ сообщит что-то новое и полезное другим, таким же заблудшим душам, как и я.
Известные ограничения
Есть два основных ограничения, которые я хочу обсудить перед завершением этой статьи. Первое из них связано с ещё более значительной минимизацией СКО.
Доводка при помощи K-средних
Как мы уже знаем, деление по среднему позволяет грубо оценить оптимальную палитру. Что можно было бы сделать — так это использовать этот алгоритм на первом шаге перед доводкой. Например, можно было бы в качестве постобработки прогнать несколько итераций алгоритма K-средних (можно предусмотреть специальный пользовательский элемент управления, регулирующий, сколько таких итераций будет сделано, и насколько глубокая доводка потребуется). Общая идея K-средних заключается в постепенном продвижении каждого цвета по отдельности в сторону более приемлемой клеточки, то есть, до клеточки, цветовое расстояние от которой до среднего цвета данной области будет меньше. Я приступил к реализации этой фичи самым наивным образом, так что у меня получилось крайне медленное решение, но этот вопрос заслуживает дальнейшего исследования, так как сделанное мной определённо приводит к улучшению результата.
По-видимому, в большинстве академических источников рекомендуется использовать кластеризацию по K-средним, но все эти решения требуют того или иного разгонного этапа. Некоторые сопровождаются определённой эвристикой, в каких-то используется анализ главных компонент (PCA), но мне пока предстоит увидеть при первом прогоне вариант, основанный на делении по среднему. Может быть, это не слишком хорошая идея, но кто знает.
Перекос в сторону визуального осветления
Ещё одна более гнетущая проблема, для которой я пока не нашёл решения, связана с человеческим восприятием: наш глаз гораздо лучше различает перемены в освещении, чем переходы оттенков. Если вы посмотрели первую демку с попугаем, то, возможно, заметили, что клеточки там кажутся тонкими. Дело в том, что компоненты a и b (отражающие, соответственно, степень зелёности/красноты и голубизны/желтизны оттенка) характеризуются гораздо меньшей амплитудой по сравнению с L (воспринимаемой осветлённостью).
Вот покомпонентное сравнение распределения цветов между растянутым и нормализованным представлением:
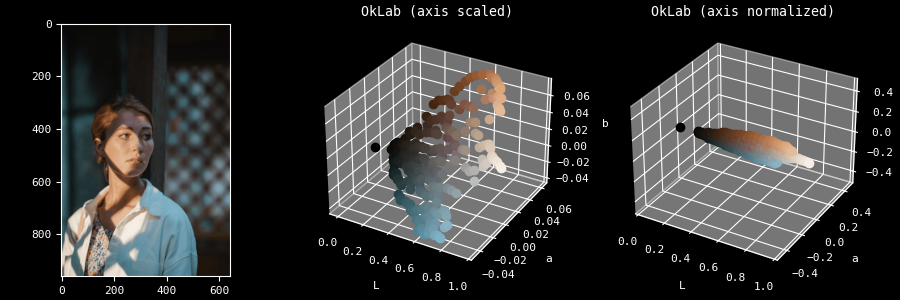
Вы вправе спросить, а есть ли в этом проблема. На практике это означает, что при низких K (скажем, менее 8 или даже 16), разрезы через L почти всегда окажутся более предпочтительными, из-за чего оттенки га картинке окажутся сильно выхолощены. Дело в том, что программа пытается сохранить осветлённость — наиболее существенный атрибут с точки зрения человеческого восприятия.
4 цвета | 8 цветов | 12 цветов | 16 цветов |

В данном случае видно, что оттенок скромно держится в районе K=16 (конкретно, он начинает значительно усиливаться от разреза K=13 и далее).
Заключение
Пока я в основном закончил работать над этим «недельным проектом», на который на самом деле уделил 2 или 3 месяца жизни. Вероятно, набор патчей FFmpeg вскоре будет поднят в главную ветку, так что, надеюсь, в следующем релизе им сможет воспользоваться каждый. Кроме того, в нём предусматриваются дополнительные методы сглаживания, реализация которых на самом деле стала для меня лёгкой интермедией на фоне всех описанных тягот. В проделанной работе по-прежнему можно многое улучшить, но для меня эта история на этом пока заканчивается.
