[Перевод] Считаем кур, пока их не заклевали06.02.2018 13:03

Эта история началась с короткой статьи в New York Times о Люке Робитейле, 13-летнем школьнике из Юлесса, штат Техас, который выиграл Raytheon Mathcounts National Competition, правильно ответив на следующий вопрос:

В амбаре кружком сидят 100 кур. Каждая из кур случайным образом клюёт свою ближайшую соседку слева или справа. Каково ожидаемое количество кур, которых никто не клюнул?

Судя по статье Times, Робитейлу потребовалось на ответ меньше секунды.

На следующий день Джордан Элленберг твитнул такую задачу:

Text of Ellenberg's tweet: 100 chicks in a circle. Each pecks R or L at random. Pecked chicks don't peck. Iterate until no two unpecked chicks adjacent. How many left?

»100 кур сидят в круге. Каждая клюёт случайным образом R или L. Клюнутые куры никого не клюют. Итерации проводятся до тех пор, пока не останется двух соседних неклюнутых кур. Сколько кур осталось?»

Мне не нужно умещать эту историю в 140 символов, поэтому я дополню вопрос Элленберга подробностями так, как я его понял. Исходная задача относилась к одной итерации синхронизированного случайного клевания, а теперь у нас есть несколько итераций. Во время одной итерации каждая курица случайным образом поворачивается влево или вправо и клюёт одну из своих соседок. Однако если курицу уже клюнули, она больше никогда не клюёт, даже её продолжают клевать. Если две соседние курицы клюют друг друга в одной итерации, обе они вылетают из игры на все последующие раунды. Если неклюнутая курица оказывается между двумя клюнутыми, её уже никогда не клюнут и поэтому она может клевать бесконечно. Вопрос заключается в том, какая часть кур выживет и станет «неуязвимыми»?

Ниже представлены спойлеры, так что сейчас вы можете попробовать ответить на вопрос сами. Пока вы этим занимаетесь, я немного поговорю о курах и о риторике и семиотике математических «текстовых задач».

Единственные мои знания о домашней птице взяты из поездки на ферму моей тёти Норетты в южном Нью-Джерси. Нельзя сказать, что мой опыт велик, но стоит заметить, что я никогда не видел куриц, сидящих вкруг, клюющих друг друга случайным образом. (У них есть порядок клевания!) Более того, я никогда не замечал в их социальных взаимодействиях чего-то, напоминавшего принцип «подставь другую щёку», который демонстрируют куры из описанной задачи. Почему клюнутая курица больше никогда не клюёт? Это ещё большая загадка, чем количественный вопрос, на который нам предстоит ответить. Открылась ли курице внезапно мудрость и сила непротивления насилию? У меня есть другое объяснение, но оно не подходит для чувствительных людей: возможно, клюнутые курицы не клюют в ответ, потому что клевки убивают наповал.

Я знаю, что глупо требовать от подобной истории реализма повествования. Математические текстовые задачи относятся к жанру, в котором никто не ожидает правдоподобия. Они происходят в мире, где лжецы всегда лгут, а рыцари всегда говорят правду, где потерпевшие кораблекрушение моряки одержимы возможностью делимости горы кокосов, где люди не знают цвет шляпы, которая на них надета. Даже законы физики склоняются перед математическими потребностями: муха, летающая между двумя сближающимися поездами, мгновенно меняет своё направление. Эти сидящие в кругу куры — не пушистые комки жёлтого пуха; они — математические абстракции. У них нет перьев, зато есть координаты и переменные состояния.

Меня вполне устраивают абстракции; давайте любыми средствами избавляться от избыточных подробностей. Тем не менее, разве смысл текстовых задач не в том, чтобы связать математику с какими-то аспектами знакомого читателям опыта? Вспомните древнюю знаменитую задачу о пересечении реки, в которой волка нельзя оставлять с козой, которую в свою очередь нельзя оставлять с капустой (прим. пер.: в оригинале лиса, курица и мешок кукурузы). Эти ограничения легко понять, если ты что-то знаешь о вкусовых предпочтениях волков и кур. Однако такая интуитивная помощь не применима к задаче с клеванием. Напротив, чем больше мы знаем об истинном поведении пернатых, тем более сбивающей с толку будет эта задача.

Ну да ладно. Приступим! Есть ли у вас уже собственный ответ?

Задача с одной итерацией из соревнований Mathcounts Competition сводится к старейшему трюку в учебнике по теории вероятностей. Курица остаётся неклюнутой, только если обе её соседки отвернулись и клюнули в другом направлении. Вероятность избежания клевка слева и справа равна $\frac{1}{2}$ . Два этих события независимы, поэтому вероятность остаться неклюнутой с обеих сторон равна $\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}$ . Эти рассуждения одинаково применимы ко всем птицам в кругу, поэтому нужно ожидать, что невредимыми останутся 25 процентов кур.

Согласны ли вы с этим анализом? Когда читал статью в Times, я дошёл до него довольно быстро (конечно, совсем не так быстро, чтобы опередить нажавшего на кнопку Люка Робитейла). Но потом у меня зародились сомнения. Строго ли верно то, что соседки курицы слева и справа совершенно независимы? В конце концов, они связаны цепочкой других кур. Возможно, по кругу может распространиться какое-то влияние, создающее корреляции между левой и правой курицей и меняющее вероятность выживания.

Настало время экспериментов: напишем программу и запустим симуляцию. Выстроим кольцо из 100 неклёванных кур и выполним одну итерацию случайного одновременного клевания. Повторим много раз и вычислим среднее количество оставшихся неклюнутыми птиц. (Вот краткая запись: пусть $N$ — число кур в кольце, а $S$ — количество оставшихся неклюнутыми. Я обозначу как $\bar{S}$ среднее значение $S$ , усреднённое после $R$ повторений эксперимента.) Мои результаты:

	$\bar{S}$
100	24,79
10 000	24,9881
1 000 000	25,000274
100 000 000	24,99991518

Как и ожидалось, среднее значение довольно близко к 25 выжившим. Более того, при каждом увеличении размера выборки в 100 раз точность аппроксимации увеличивается примерно в десять раз. Этот паттерн соответствует эмпирическому правилу статистики: флуктуации случайного процесса пропорциональны квадратному корню размера выборки. То есть незначительные отклонения от $\bar{S} = 25$ похожи на невинный случайный шум, а не какое-то систематическое смещение.

То есть вопрос решён, не так ли?

Вообще, симуляция выглядит довольно убедительной для конкретного случая $N = 100$ кур, но результат может отличаться для других значений N. В частности, возможно, существует некий эффект конечной размерности, становящийся очевидным только при малых N. Рассмотрим «круг» из всего двух кур. В этой симуляции левый и правый сосед — это одна и та же курица! Вне зависимости от случайно сделанных выборов две курицы сразу же клюнут друг друга, и часть выживших будет равна не 25 процентам, а нулю.

Следующий, более крупный «круг» состоит из трёх кур, собранных в треугольник. Два соседа теперь — это разные куры, но они также являются соседями друг друга. Что случится, когда три курицы набросятся друг на друга? В системе есть $2^3 = 8$ возможных комбинаций клевания, и мы легко можем изучить из все. Стрелками на схеме показано то, в какую сторону курицы выбрали клевать.

В двух случаях все курицы клюют влево или клюют вправо, и выживших нет. В каждом другом случае неклюнутой остаётся ровно одна курица. Собрав все восемь комбинаций, мы получаем шесть неклюнутых кур из 24, то есть соотношение равно $\bar{S} = \frac{1}{4}$ . То есть, похоже, аномалия конечных значений затрагивает только случай задачи с двумя курами.

Но постойте! Существует ещё один возможный искажающий результаты фактор. Можем ли мы быть уверены, что одинаковые результаты будут и для чётных, и для нечётных количеств кур? При любом нечётном значении N существует только один способ уничтожить всех кур за один раунд: все они должны клевать в одном направлении. Однако при чётном N к немедленному вымиранию приводит ещё одна комбинация: соседние куры разбиваются на пары и клюют друг друга. Не изменит ли этот дополнительный способ общую вероятности выживания?

Давайте посмотрим, что происходит при N = 4. Теперь существует $2^4 = 16$ возможных результатов:

Как и ожидалось, в четырёх комбинациях вообще нет выживших. С другой стороны, также есть четыре комбинации, в которых остаётся не одна, а две неклюнутые курицы. Дополнительные потери и дополнительные выигрыши чудесным образом уравновешивают друг друга. Всего у нас будет 16 выживших из 64 кур, то есть соотношение снова равно $\bar{S} = \frac{1}{4}$ .

После этого долгого и извилистого обхода комбинаторики клевания кур мы вернулись ровно к тому, с чего начинали. Вероятность остаться неклюнутой после одной итерации клевания равна $\frac{1}{4}$ для любого $N \gt 2$ . Все мои волнения об эффектах конечных размеров и неравномерностей чёт-нечет были пустой тратой времени. Так зачем же я поделился ими с вами? Хотя мои волнения оказались ничем не обоснованными, они вовсе не надуманны. Даже небольшие изменения в порядке клевания приведут к другим результатам. Допустим, клевание будет последовательным, а не одновременным. Одна выбранная курица начинает последовательность клевков, а затем свои ходы делают другие птицы, расположенные по часовой стрелке от неё. Когда приходит очередь курицы, то если её уже клюнули, то она ничего не делает. Если её не клюнули, она клюёт влево или вправо, выбирая случайным образом. Итерация заканчивается, когда каждая курица сделает свой ход.

При $N = 2$ легко увидеть, что первая клюющая курица всегда выживает, а другая всегда умирает, то есть доля выживших равна $\frac{1}{2}$ . Немного посчитав куриц на бумаге, можно выяснить, что доля выживших в 50 процентов также справедлива и для $N = 3$ . При исследовании бОльших значений $N$ компьютерные эксперименты показывают, что доля выживших при стремлении $N$ к бесконечности снова приближается к $\frac{1}{2}$ . Однако между этими предельными значениями существуют забавные ситуации:

При $N = 4$ доля выживших опускается ниже 0,47. (Точная вероятность равна $\frac{30}{64} = 0.46875$ .) Это минимум значений. Но при возвращении соотношения к 0,5 в кривой появляются колебания, показывающие расхождения результатов при чётном и нечётном количествах: вероятность выживания снижается больше для чётных N, чем для нечётных N. Именно такое поведение я искал (но не нашёл) в исходной версии задачи с соревнований Mathcounts.

Давайте снова возьмёмся за задачу Элленберга про итерируемое клевание (с одновременным, а не последовательным клеванием). Мы уже знаем, что после первой итерации можно ожидать, что неклюнутыми останется примерно четверть кур. Очевидно, что часть неклюнутых не может увеличиваться после нескольких итераций. То есть в конечном состоянии ожидаемая доля выживших $\bar{S}$ должна находиться где-то между нулём и $\frac{1}{4}$ .

Полезно будет посмотреть на обычную конфигурацию клюнутых (●) и неклюнутых (○) кур после одной итерации синхронизированного клевания:

●○●●●○○●●●●○●●○●●○○●●●○○●●●●●○●●●●●●●●●○○●●●●●●○○●●●○●●●●●●○●●●○○●●●●●

(Мысленно соедините левый и правый концы массива, чтобы создать кольцо.) Заметьте, что здесь присутствуют длинные строки клюнутых кур, но неклюнутые куры присутствуют только в двух конфигурациях. Они являются или одиночками (●○●), или парами (●○○●). Причину такого паттерна понять просто. После раунда клевания существование группы из трёх неклюнутых кур подряд (●○○○●) невозможна. Средняя курица обязана клюнуть влево или вправо, то есть у неё не может быть двух неклюнутых соседей.

Такие ограничения упрощают анализ последующих итераций. Одиночки в сущности бессмертны и неизменяемы: неклюнутую курицу посередине никогда больше не клюнут, а клюнутых соседей никогда больше не вернуть в «неклюнутое» состояние. Для пар существует четыре возможных варианта развития событий, соответствующих четырём способам, которыми две активные курицы выберут клевать:

В любой итерации все эти четыре события имеют одинаковую вероятность, а именно $\frac{1}{4}$ . Первые три получившихся состояния являются заключительными, в том смысле, что дальнейшие итерации клевания не изменят их. В четвёртом случае у нас снова остаётся пара соседей, перед которой в следующей итерации предстанет тот же выбор вариантов. Со временем, когда количество итераций будет стремиться к бесконечности, четвёртый случай должен привести к одному из других результатов, а потому в длительной перспективе мы должны считать вероятность четвёртого случая равной нулю, а вероятность каждого из других трёх случаев равной $\frac{1}{3}$ .

Теперь настало время соединить эти зависящие от обстоятельств события вместе и вычислить вероятность выживания курицы в длительной перспективе. На рисунке ниже показана схема. В первом раунде клевания три четверти кур сразу же уничтожаются. Из оставшейся четверти половина является одиночками, которые выживают бесконечно. Каждая другая выжившая курица является членом пары, а другая клюющая курица из её пары — это её левая или правая соседка.

В нижней части схемы подводится итог влияния всех последовательных итераций, которые продолжаются, пока все пары не уничтожатся или не уменьшаться до одиночек. (Я называю это клеванием до последнего.) Для каждого пути, ведущего к выживанию одиночки, вероятность является произведением отдельных вероятностей, встреченных на этом пути. Существует три таких пути с вероятностями $\frac{1}{8}$ , $\frac{1}{48}$ и $\frac{1}{48}$ и суммой $\frac{1}{6}$ .

Должен признаться, что мне не удалось выполнить этот анализ — или получить верный ответ — с первой попытки. Я добился его только после выполнения симуляции, узнав таким образом, что мне нужно искать. И даже тогда у меня возникали проблемы с двойным подсчётом.

Вот как выглядят результаты симуляции:

	$\bar{S}$
100	16,53
10 000	16,6835
1 000 000	16,664404
100 000 000	16,66701664

Заметьте, что точность снова улучшается как квадратный корень от размера выборки, несмотря на то, что дисперсия здесь больше, чем в эксперименте с одной итерацией.

А как насчёт эффектов конечного размера? В кругу со всего двумя или тремя курами их судьба полностью определяется единственной итерацией клевания: $\bar{S}$ соответственно равно 0 и $\frac{1}{4}$ . То есть эти наименьшие круги не соответствуют правилу $\frac{1}{6}$ , но похоже, что круги любого бОльшего размера сводятся к $\frac{1}{6}$ . Расхождений чёт-нечет в них не замечено.

Ещё одним подходом к пониманию задачи итерированного клевания кур является теория цепей Маркова. Для кольца из $N$ кур мы перечисляем все $2^N$ состояний и назначаем вероятность каждому переходу между состояниями. Рассмотрим кольцо из четырёх кур, которое имеет 16 состояний. Симметрия позволяет нам объединить некоторые из состояний; другие состояния можно отбросить, потому что они недостижимы из начального состояния с четырьмя неклюнутыми курами ().

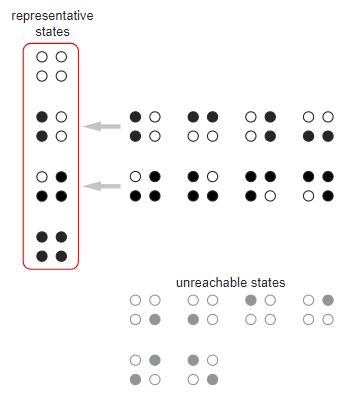
В модели должны сохраниться только четыре состояния выделенные красным контуром. Переходы между ними записываются в направленный граф, в котором каждая стрелка помечается соответствующей вероятностью. Стоит заметить, что у начального состояния есть только исходящие стрелки; после выхода из него туда невозможно вернуться. Состояния и являются поглощающими: единственная исходящая стрелка ведёт обратно в то же состояние; то есть однажды попав в одно из этих состояний, вы уже из него не выберетесь.

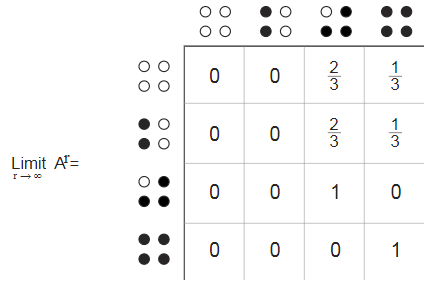
Важную информацию из этого направленного графа можно отобразить в матрице $4 \times 4$ , в которой строки и столбцы помечены четырьмя состояниями, а элементы матрицы представляют собой вероятность перехода из состояния строки в состояние столбца. Сумма элементов каждой строки равна 1, как и должно быть, если они представляют собой вероятности.

Паттерн нулевых элементов в матрице переходов подразумевает, что в некоторые состояния нельзя попасть из других состояний, даже непрямым путём. По этой причине говорят, что марковская модель является иррегулярной. Это немного неприятно, потому что регулярные марковские модели проще в анализе и понимании. В регулярной модели, когда мы берём последовательные степени матрицы перехода, она сводится к установившемуся состоянию, в котором все строки одинаковы, а каждый столбец состоит из единственного повторяющегося значения. Такое фиксированное состояние отображает распределение вероятностей в долгосрочной перспективе. Иррегулярная марковская модель может даже не иметь установившегося ограничивающего распределения, но в нашей оно есть, и это даёт нам определённые подсказки. Любое кольцо из четырёх кур должно в результате прийти к одному из двух поглощающих состояний. С вероятностью «две третьих» это заключительное состояние будет и с вероятностью «одна третья» . Этот результат соответствует вычисленной одной шестой доле неклёванных кур.

То есть можно подводить итог, правда? И в задаче с соревнований, и в её итеративной версии Элленберга спрашивалось ожидаемое количество выживших кур, и мы дали ответ: при $N$ кур ожидаемое количество выживших $\bar{S}$ равно $\frac{N}{4}$ после единственной итерации клевания и $\frac{N}{6}$ при клевании до конца. Однако иронично, что ожидаемое значение вероятностного процесса не обязательно сообщает нам, чего стоит ожидать. Рассмотрим простую задачу: подбросив монетку 100 раз, сколько «орлов» мы ожидаем увидеть? Очевидный ответ — 50, и он верен в том смысле, что никакое другое число не имеет большей возможности верно предсказать результат эксперимента. Однако вероятность увидеть ровно 50 «орлов» равна всего 0,08, то есть в 90 процентах случаев мы будем получать другое число.

Вместо того, чтобы смотреть только на ожидаемое значение, давайте изучим интервал возможных значений $S$ игры с клеванием. Мы уже установили, что ноль выживших является возможным результатом, то есть нижняя граница у нас есть. А что насчёт верхней границы — максимального количества выживших? В процессе с одной итерацией клевок делает каждая курица, то есть после этой итерации у каждой курицы должен быть хотя бы один клюнутый сосед. На основании этого факта я заявляю, что выжившая популяция никогда не может быть больше $\frac{N}{2}$ . (Вы согласны? Мне понадобилось какое-то время, чтобы убедить себя в этом.)

Если $S$ никогда не может быть больше $\frac{N}{2}$ , то следующим вопросом будет такой: сможет ли оно вообще когда-нибудь достичь этого предела? И если у нас может быть одинаковое количество клюнутых (●) и неклюнутых (○) кур, то как они будут расположены в кольце? Кажется логичным предложить следующую конфигурацию:

●○●○●○●○●○●○

Это стабильное состояние: неклюнутых кур никогда не смогут клюнут, то есть дальнейшие изменения невозможны. А доля выживших равна $\frac{1}{2}$ . Но у этой схемы есть проблема: её невозможно достичь из начального состояния. Посмотрите на любую из клюнутых кур и задайте вопрос: какая из соседок её клюнула? Очевидно, что ни одна из них, потому что их обеих никто не клюнул. Но это невозможно, потому что каждая курица в первой итерации должна клюнуть.

Хотя схему из попеременных чёрных и белых кур мы исключили, мы находимся на верном пути. Существует ещё одна конфигурация, при которой после первой итерации тоже остаётся половина кур, и эта схема достижима из начального состояния:

●●○○●●○○●●○○

Когда мы соединяем концы, чтобы получить кольцо, у каждой курицы, вне зависимости от того, клюнули её или нет, есть одна клюнутая соседка. Оказывается, что это единственный способ, если не считать очевидных симметричных случаев, чтобы достичь выживания 50 процентов. (Строго говоря, 50 процентов можно достичь только когда $N$ делится на 4, но $S$ никогда не меньше $\frac{N-2}{2}$ .)

Когда клевание выполняется до победного конца, верхняя граница $S = \frac{N}{2}$ больше недостижима. Допустим, что мы бы пытались сохранить $\frac{N}{2}$ через несколько итераций клевания. Очевидно, что нам пришлось бы начинать в первой итерации с максимальной доли выживших ●●○○●●○○●●○○. Однако по крайней мере половина неклюнутых кур в этой конфигурации должна погибнуть в последующих итерациях, оставив не больше $\frac{N}{4}$ выживших.

Значит ли это, что $S = \frac{N}{4}$ является максимально возможным значением после клевания до победного конца? Нет, не значит. Существует ещё одна схема, в которой выживает одна из каждых трёх кур:

●●○●●○●●○●●○

Эта конфигурация достижима за одну итерацию и бесконечно устойчива, потому что ни у одной из клюющих кур нет клюющих соседок. Ни одна другая схема не имеет большей плотности выживших при выполнении процесса клевания до конца.

Подведём итог: после одной итерации клевания количество выживших кур должно находиться где-то между нулём и $\frac{N}{2}$ , а ожидаемое количество $\bar{S}$ — ровно посередине, в $\frac{N}{4}$ . После завершения всех последующих итераций количество неклюнутых кур будет находиться в интервале между нулём и $\frac{N}{3}$ , а ожидаемое значение снова будет посередине, в $\bar{S} = \frac{N}{6}$ .

«Сколько кур выживет?» — этот вопрос, кажется, требует численного ответа, но на самом деле наиболее информативным ответом на него будет совсем не число, а распределение:

Каждая кривая фиксирует результаты миллиона экспериментов с кольцом из 100 кур, показывая частоту каждого возможного значения $S$ . Как и ожидалось, распределение при одной итерации имеет пик на 25 выживших, а кривая задачи с итерацией — на 17 (ближайшее к $\frac{100}{6}$ целое). Заметьте, что красная кривая не только смещена влево, но также выше и уже.

Чтобы лучше рассмотреть результаты, давайте изменим масштаб. Чтобы кривые были более плавными, я перейду к экспериментам с $N = 10000$ кур. Зелёная кривая — для одной итерации, а красная — для эксперимента со множеством итераций клевания:

При бОльших значениях $N$ пики кривых находятся в 2500 и в 1666,67, то есть ровно в точках, ожидаемых для $\frac{N}{4}$ и $\frac{N}{6}$ . Было неудивительно найти пики в этих точках, но что же управляет шириной и общей формой кривой? Другими словами, каковая математическая природа распределений?

Первая догадка — всегда стоит попробовать нормальное (или гауссово) распределение. Для задачи клевания нормальное распределение определяет $P(S)$ , вероятность наблюдения $S$ выживших, следующим образом:

$P(S) = \frac{1}{\sigma\sqrt{2 \pi}} \exp -\frac{1}{2}\left(\frac{S - \mu}{\sigma}\right)^2$

Довольно запутанное уравнение для такого знакомого понятия, но из него можно выделить основной смысл. Уравнение определяет симметрическую кривую с пиком, где $S$ равно $\mu$ , то есть среднему значению распределения. Ширина пика зависит от стандартного отклонения $\sigma$ . Поскольку площадь под кривой постоянна, $\sigma$ в сущности определяет её высоту: более узкий пик должен быть выше.

Мы можем согласовать нормальное распределение с данными о клевании с помощью процедуры, находящей оптимальные значения $\mu$ и $\sigma$ , такие, которые минимизируют расхождение между точками данных и математической моделью. В двух представленных ниже графиках согласованные модели наложены на два графика данных, первая для одной итерации, вторая — для итераций до конца:

Согласование выглядит достаточно близким, теоретические кривые разделяют экспериментальные от начала до конца. В каком-то смысле, этот результат можно считать успехом, но я всё-таки не нахожу такой подход к задаче полностью удовлетворительным. Нормальная кривая создаёт очень хорошую описательную модель процесса клевания, но не прогнозирует и не объясняет её. Не забывайте, что мы согласовали кривую с данными, а не наоборот. Я не вижу очевидных способов создать некое нормальное распределение из того, что я знаю о взаимодействиях клюющихся кур. В частности, откуда берутся значения $\sigma$ двух моделей? Почему $\sigma \approx 25$ в модели с одной итерацией, но $\sigma \approx 23.6$ в модели с множеством итераций? Эти значения выглядят как независимые параметры, которые нам приходится подгонять для соответствия данным. Более того, они будут разными для каждого значения $N$ . Ещё одна проблема: нормальная кривая — это непрерывное распределение, определённое на всей вещественной числовой оси. Функция клевания дискретна, она имеет смысл только для целых величин.

Давайте отложим в сторону нормальную кривую и рассмотрим ещё одну правдоподобную модель: биномиальное распределение, которое дискретно и возникает во многих контекстах, связанных с вероятностями. Предположим, что мы бросим 10 000 костей и посчитаем, на скольких из них выпала единица. Когда мы повторим эксперимент множество раз, ожидаемое количество единицы будет равно одной шестой от 10 000, то есть то же значение, что и ожидаемое количество выживших в итерируемом эксперименте с клюющимися курами. Для костей существует хорошо известное математическое выражение, определяющее не только ожидаемое значение, но и форму всего распределения. Предположим, что каждая кость имеет вероятность выбрасывания $1$ , обозначенную $p$ . Мы будем бросать $N$ костей и нам нужно знать вероятность увидеть $k$ единицы= для любого $k$ от $0$ до $N$ . Формула для обработки этой информации имеет вид:

$P(k) = {N \choose k} p^k (1 - p)^{N - k}$

Здесь $p^k (1 - p)^{N - k}$ даёт вероятность любой отдельной комбинации $k$ единиц среди $N$ костей. Биномиальный коэффициент $N \choose k$ , равный $N! / k! (N-k)!$ \), подсчитывает количество таких комбинаций.

При $N = 10000$ и $p = \frac{1}{6}$ мы получаем кривую, показывающую результат вышеупомянутого эксперимента с бросанием костей. Возможно, та же кривая описывает и то, что происходит в модели клевания со множеством итераций, которая имеет то же ожидаемое значение? Увы, но нет.

Биномиальная кривая шире и более плоская, чем распределение выживших при итерированном клевании. Что же пошло не так? Когда я впервые увидел график, у меня появилось предчувствие. Как сказано выше, биномиальный коэффициент $N \choose k$ подсчитывает все способы выбора $k$ элементов из множества размером $N$ . Он подходит для эксперимента с костями, потому что все возможные комбинации $k$ успехов среди $N$ равновероятны. В частности, когда мы бросаем © Habrahabr.ru