[Перевод] Ричард Хэмминг: Глава 9. N-мерное пространство05.02.2018 12:18

Привет, Хабр. Помните офигенную статью «Вы и ваша работа» (+219, 2222 в закладки, 350k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводи, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 6 (из 30) глав.

Глава 9. N-мерное пространство

(За перевод спасибо Алексею Фокину, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

Когда я стал профессором после 30 лет активных исследований в Bell Telephone Laboratories главным образом в отделе математических исследований, я вспомнил, что профессора должны осмыслять и резюмировать прошлый опыт. Я положил ноги на стол и стал обдумывать свое прошлое. В ранние годы я занимался в основном вычислениями, то есть я был вовлечен во многие большие проекты, требующие вычислений. Думая о том, как были разработаны несколько больших инженерных систем, в которые я был частично вовлечен, я начал, находясь теперь на некотором расстоянии от них, видеть, что у них было много общих элементов. Со временем я начал понимать, что задачи проектирования находятся в n-мерном пространстве, где n — число независимых параметров. Да, мы создаем 3-мерные объекты, но их проектирование находится в многомерном пространстве, 1 измерение для каждого проектируемого параметра.

Многомерные пространства понадобятся для того, чтобы дальнейшие доказательства стали интуитивно понятны без строгой детализации. Поэтому мы будем сейчас рассматривать n-мерное пространство.

Вы думаете, что живете в трехмерном пространстве, но во многих случаях вы живете в двумерном пространстве. Например, в случайном ходе жизни, если вы встретите кого-то, то имеете разумный шанс встретить этого человека снова. Но в мире 3-х измерений этого шанса нет! Рассмотрим рыб в океане, которые потенциально живут в трех измерениях. Они двигаются по поверхности или по дну, ограничивая вещи до двух измерений, или они ходят в школы, или собираются в одном месте в одно и то же время, например таком как устье реки, пляж, Саргассово море и т.д. Они не могут ожидать встретить приятеля, если они будут странствовать в открытом океане в трех измерениях. Или, к примеру, если вы хотите, чтобы самолеты столкнулись вы должны собрать их рядом с аэропортом, поместить их в двумерные уровни полетов, или послать их группой; действительно случайные полеты имели бы меньше аварий, чем это происходит сейчас!

N-мерное пространство является математической конструкцией, которую мы должны исследовать, чтобы понять что случается с нами, когда мы бродим там при решении задач проектирования. В двух измерениях у нас есть теорема Пифагора, для прямоугольного треугольника квадрат гипотенузы равен сумме квадратов других сторон. В трех измерениях нас интересует длина диагонали параллелепипеда, Рис. 9.1. Чтобы найти ее мы сначала проводим диагональ одной грани, применяем теорему Пифагора, затем берем ее как одну из сторон с другой стороной третьего измерения, которая перпендикулярна ей, и снова из теоремы Пифагора получаем, что квадрат диагонали ест сумма квадратов трех перпендикулярных сторон. Очевидно следует из этого доказательства и необходимой симметрии формулы, что если вы поднимаетесь к более высоким измерениям у вас все также квадрат диагонали будет равен сумме квадратов попарно взаимно перпендикулярных сторон,

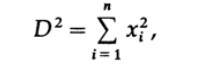
где xi длины сторон прямоугольного блока в n-мерном пространстве.

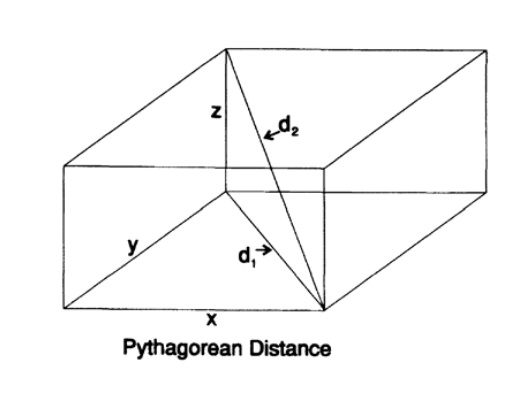
Рис. 9.I

Продолжая геометрический подход, плоскости в пространстве будут просто линейными комбинациями xi, а сфера вокруг точки будет всеми точками, находящимися на одном фиксированном расстоянии от заданной.

Нам понадобится объем n-мерной сферы, чтобы понять идею размера куска ограниченного пространства. Но сначала нам надо приближение Стирлинга для n!, которую я выведу, чтобы вы поняли большинство деталей и были уверены в правильности того, что последует, а не верили на слово.

С произведением типа n! трудно обращаться, поэтому мы возьмем log n!, который становится

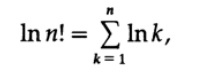
где, конечно, ln логарифм по основанию e. Суммы напоминают нам, что они связаны с интегралами, поэтому мы начнем с такого интеграла

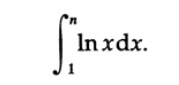
Мы применяем интегрирование по частям (так как знаем, что ln x происходит из интегрирования алгебраической функции и, следовательно может быть исключен на следующем шаге). Пусть U=ln x, dV=dx, тогда

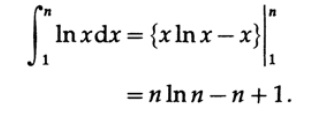
С другой стороны, если мы применим формулу трапеции к интегралу ln x мы получим, см. Рис. 9.II,

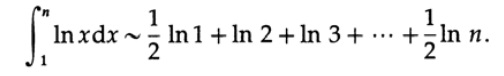
Так как ln 1 = 0, прибавляя (½) * ln n к обоим частям равенства мы в итоге получаем

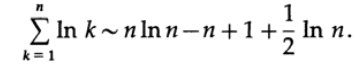
Избавимся от логарифмов, возводя e в степень обеих частей.

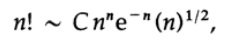
где С некая константа (близкая к e), не зависящая от n, так как мы аппроксимировали интеграл флрмулой трапеции, погрешность растет все медленнее и медленнее при увеличении n

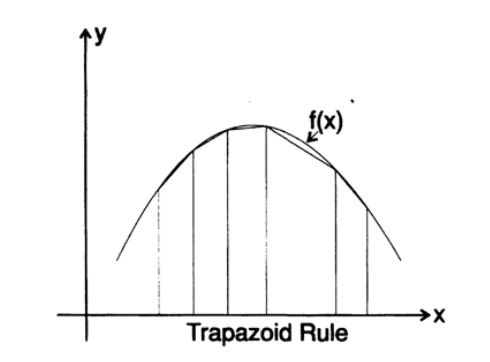
Рис. 9.II

все больше и больше, C имеет предел. Это первая форма формулы Стирлинга. Мы не будем тратить время на вычисление предела константы С при стремлении к бесконечности, который оказывается √(2*π)=2.5066… (e=2.71828…). Таким образом окончательно получаем формулу Стирлинга для факториала

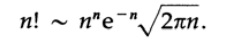
Следующая таблица показывает погрешность приближения Стирлинга для n!

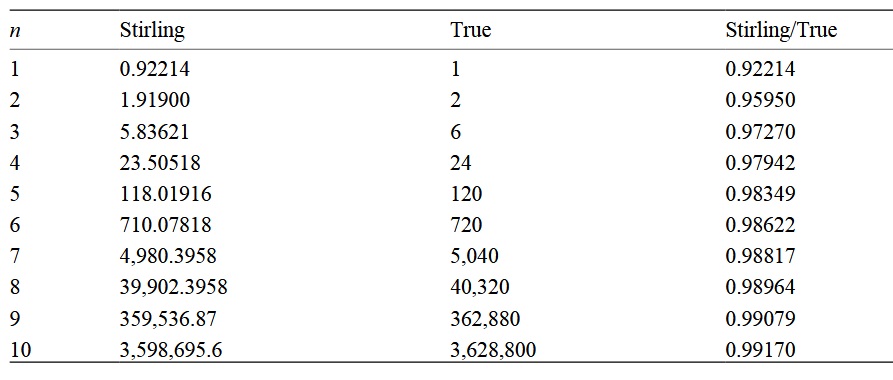
Обратите внимание, что при увеличении чисел коэффициент приближается к единице, но разница становится все больше и больше!

Если вы рассмотрите 2 функции

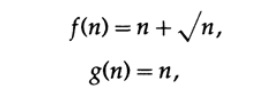
то предел отношения f (n)/g (n) при n, стремящемся к бесконечности, равен 1, но как и в таблице разница

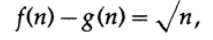
становится все больше и больше при возрастании n.

Нам надо расширить понятие факториала на множество всех положительных действительных чисел, для этого мы введем гамма функцию в форме интеграла

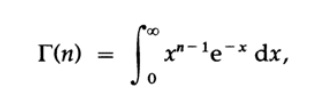
который существует для всех n>0. Для n>1 мы снова интегрируем по частям, в этот раз используем dV=e^(-x)dx и U = x^(n-1). Для двух пределов интегрируемая часть равна 0 и мы имеем следующую приведенную формулу

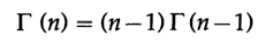
с Г (1)=1.

Таким образом, гамма функция принимает значения (n-1)! для всех положительных целых n и естественным образом расширяет понятие факториала на все положительные числа, так как интеграл существует для всех n > 0.

Нам понадобится

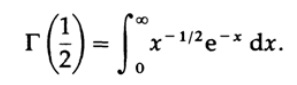
Обозначим x=t^2, тогда dx=2t*dt, и получаем (используя симметрию на последнем шаге)

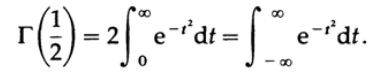
Теперь используем стандартный подход, чтобы вычислить этот интеграл. Мы получаем произведение двух интегралов, один по переменной x и один по переменной y.

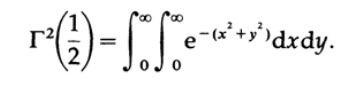
x^2 + y^2 подразумевают полярные координаты, поэтому преобразуем к виду

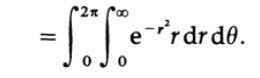
Криволинейное интегрирование (angle integration) просто. Экспонентное интегрирование теперь тоже просто, и мы в итоге получаем.

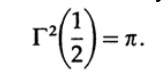
Таким образом,

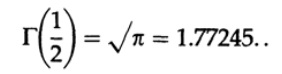
Теперь вернемся к объему n мерной сферы (или гиперсферы, если хотите). Ясно, что объем n-мерного куба со стороной x равен x^n. Немного подумав, вы поймете, что формула для объема n-мерной сферы должна иметь вид

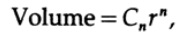
где Cn соответствующая константа. Для случая n = 2, константа равна π, для случая n=1 равна 2 (если подумать). В трехмерном случае мы имеем C3= 4*π/3.

Мы начнем с того же трюка, который использовали для гамма функции от ½ за исключением того, что в этот раз мы возьмем произведение n интегралов, каждый со своей переменной xi. Объем сферы можно представить как сумму объемов поверхностей, каждое слагаемое этой суммы соответствует площади поверхности, умноженной на толщину dr. Для сферы значение площади поверхности можно получить дифференцированием объема сферы по отношению к радиусу r,

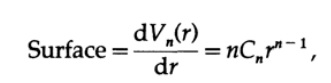
и следовательно слагаемые объема равны

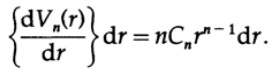
Приравнивая r^2=t, имеем

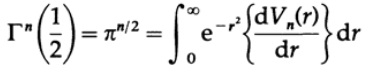
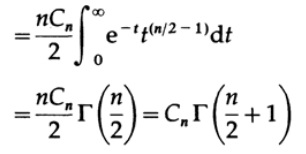
откуда получаем.

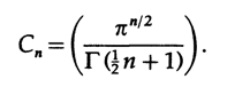
Легко видеть, что

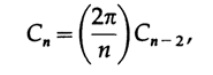
И мы можем вычислить следующую таблицу.

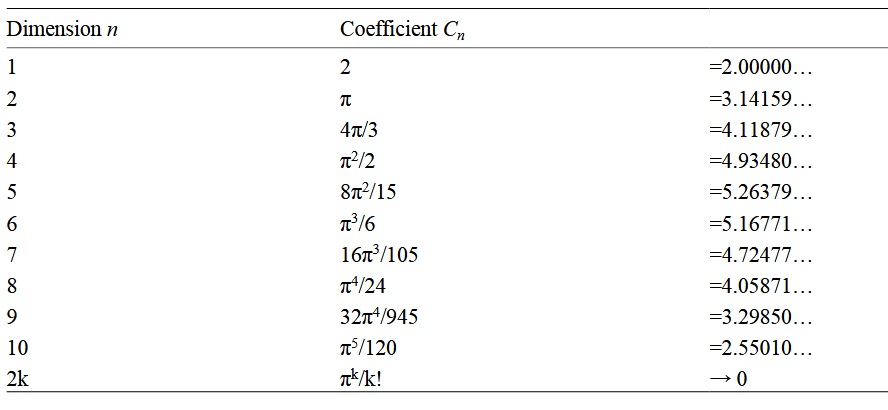
Таким образом, мы видим, что коэффициент Cn возрастает до n=5, а затем уменьшается до 0. Для сфер единичного радиуса это означает, что объем сферы стремится к нулю при увеличении размерности. Если радиус равен r, то для объема, обозначив n=2k для удобства (так как реальные числа изменяются гладко при увеличении n и сферы нечетных размерностей сложнее вычислять),

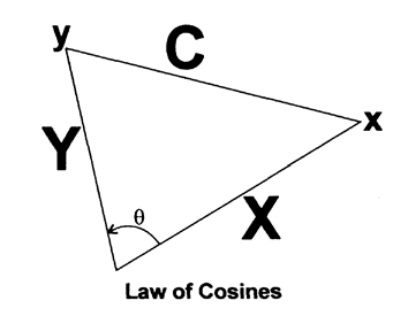
Рис. 9.III

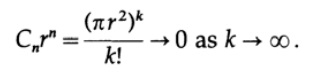
Не важно насколько велик радиус r, увеличение количества измерений n рождает сферу сколь угодно маленького объема.

Теперь рассмотрим относительное количество объема, расположенное близко к поверхности n-мерной сферы. Пусть r — радиус сферы, а внутренний радиус поверхности r (1-ε), тогда относительный объем поверхности составляет

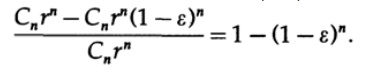
Для больших n независимо от того насколько тонка (по отношению к радиусу) поверхность внутри нее почти ничего нет. Как мы говорим объем почти весь на поверхности. Даже в 3 мерном пространстве единичная сфера имеет 7/8 объема внутри поверхности толщиной ½ радиуса. В n-мерном пространстве 1-(½)^n внутри половины радиуса от поверхности.

Это важно в проектировании; оказывается после вычислений и преобразований данных выше, что почти наверное оптимальное проектирование будет на поверхности, а не глубоко внутри как вы могли думать. Вычислительные методы обычно не годятся для поиска оптимума в многомерных пространствах. Это вовсе не странно; вообще говоря лучший дизайн — это привести один или более параметров к своему экстремуму — очевидно, что вы окажетесь на поверхности видимой области дизайна!

Следующим мы рассмотрим диагональ n-мерного куба, другими словами вектор из начала координат в точку с координатами (1,1,…,1). Косинус угла между этой линией и любой осью дается по определению как отношение значения координаты длины проекции на данную ось, которая очевидно равна 1 к длине вектора, которая равна √n. Следовательно

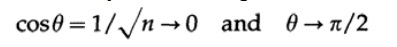
Отсюда следует, что при больших n диагональ почти перпендикулярна к каждой координатной оси!

Если мы рассмотрим точки с коодинатами (±1, ±1,…, ±1) тогда будет 2n таких диагоналей, которые все почти перепендикулярны к каждой оси координат. Для n=10, например, их количество составляет 1024 таких почти перпендикулярных линий.

Мне нужен угол между двумя векторами, и хотя вы может быть помните, что это скалярное произведение векторов, я предлагаю вывести это снова, чтобы лучше понимать то, что происходит. [Ремарка; Я обнаружил, что очень полезно в важных ситуациях пересматривать все базовые участвующие выведения, чтобы прочувствовать то, что происходит.] Возьмем две точки x и y, с соответствующими координатами xi и yi. Рис. 9.III. Применяя теорему косинусов в плоскости 3 точек x, y и начала координат, мы имеем

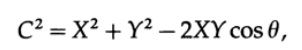
где X и Y длины отрезков до точек x и y. Но C можно получить используя разницы координат по каждой оси

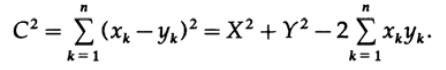
Приравнивая два выражения мы видим

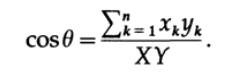
Применим теперь эту формулу для двух отрезков, проведенных из начала координат к случайной точке из набора координат

(±1, ±1,…, ±1)

Скалярное произведение двух таких множителей, взятых случайно, снова равно ±1 и это должно быть просуммированно n раз, при этом длина каждого отрезка равна √n, следовательно (заметьте n в знаменателе)

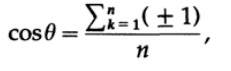
и по слабому закону больших чисел это стремится к 0 с возрастанием n почти наверное. Но существует 2^n случайных векторов и для данного вектора все остальные из 2^n случайных векторов почти наверное почти перпендикулярны данному! n-мерность действительно обширна!

В линейной алгебре и других дисциплинах вы научились находить множество перпендикулярных осей и затем представлять все остальное в этой системе координат, но вы видите, что в n-мерном пространстве после того, как вы нашли n взаимно перпендикулярных координатных осей, существуют 2^n других направлений почти перпендикулярных тем, которые вы нашли! Теория и практика линейной алгебры совершенно разные!

Наконец, для дальнейшего доказательства, что ваша интуиция о n-мерном пространстве не очень хороша, я произведу еще один парадокс, который мне понадобится в следующих главах. Начнем с квадрата 4×4, поделенного на 4 единичных квадрата, в каждом из которых мы начертим единичную окружность, Рис. 9.IV. Далее мы начертим окружность с центром в центре квадрата, касающуюся остальных с внутренней стороны. Ее радиус должен быть из Рис. 9.IV,

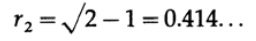
В 3-хмерном пространстве мы имеем 4×4x4 куб и 8 сфер единичного радиуса. Внутренняя сфера касающаяся остальных в точке, лежащей на отрезках соединяющих центры, имеет радиус

Подумайте, почему ее радиус больше, чем для 2 измерений.

Двигаясь к n измерениям, имеем 4×4x…x4 куб и 2^n сфер, по одной в каждом углу, каждая касается остальных n соседних. Внутренняя сфера, касающаяся изнутри всех остальных, будет иметь радиус

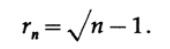
Проверьте это внимательно! Вы уверенны? Если нет, почему нет? Где ошибка в рассуждениях?
Убедившись, что это правда, применим для случая n=10 измерений. Для внутренней сферы имеем радиус

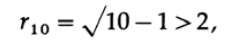
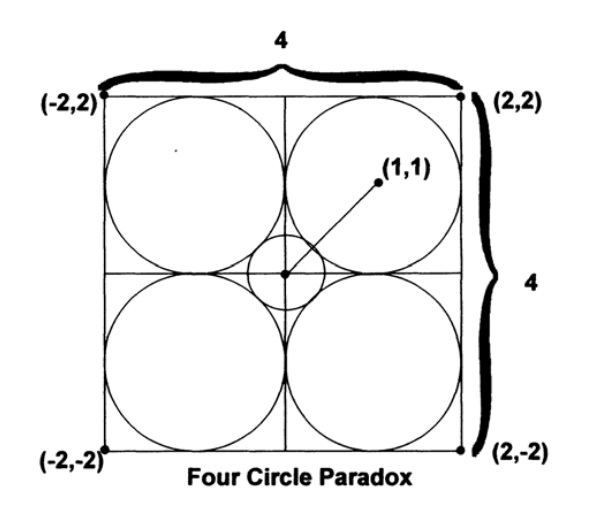
Рис. 9.IV

и в 10 мерном пространстве внутренняя сфера вышла за пределы куба. Да, сфера выпуклая, да, она касается остальных 1024 изнутри, и при этом она выходит за пределы куба!

Это слишком для вашей чувствительной интуиции об n-мерном пространстве, но помните, что n-мерное пространство это то место, где обычно происходит проектирование сложных объектов. Вы должны стараться лучше почувствовать n-мерное пространство, размышляя о только что описанных вещах, пока вы не начнете видеть как они могут быть истинными, вернее почему они должны быть истинными. Иначе у вас будут проблемы, когда вы будете решать сложную задачу проектирования. Возможно вам стоит заново вычислить радиусы разных размерностей, а также вернуться к углам между диагоналями и осями координат и посмотреть как это получается.

Сейчас необходимо строго отметить, что я сделал все это в классическом Евклидовом пространстве, используя Пифагорово расстояние, где сумма квадратов разностей соответствующих координат равна квадрату расстояния между точками. Математики называют это расстояние L2.

Пространство L1 использует не сумму квадратов разностей координат, а скорее сумму расстояний, как если вы путешествуете по городу с прямоугольно решеткой улиц. Это сумма разниц, между двумя пунктами, которая говорит вам, как далеко надо будет идти. В сфере вычислений это часто называют «расстояние Хэмминга» по причинам, которые станут понятны в последующих главах. В этом пространстве окружность в двух измерениях выглядит как квадрат, стоящий на вершине, рис. 9.V. В трехмерном пространстве это как куб, стоящий на вершине и т.д. Теперь вы можете лучше видеть как может парадоксальная внутренняя сфера из вышеприведенного примера выходить за пределы куба.

Существует третья, часто используемая, метрика (все они метрики = функции расстояния), называемая L∞, или расстояние Чебышева. Здесь за расстояние берется максимум разниц координат независимо от остальных разниц, рис. 9.VI. В этом пространстве окружность есть квадрат, 3-хмерная сфера есть куб, и вы видите, что в этом случае внутренняя сфера из парадокса имеет нулевой радиус во всех направлениях.

Это были примеры метрик, мер расстояния. Условия определения метрики D (x, y) между двумя точками x и у следующие:

1. D (x, y) ≥ 0 (неотрицательная)
2. D (x, y) = 0 тогда и только тогда, когда x=y (тождественность)
3. D (x, y) = D (y, x) (симметричность)
4. D (x, y) + D (y, z) ≥ D (x, z) (неравенство треугольника).

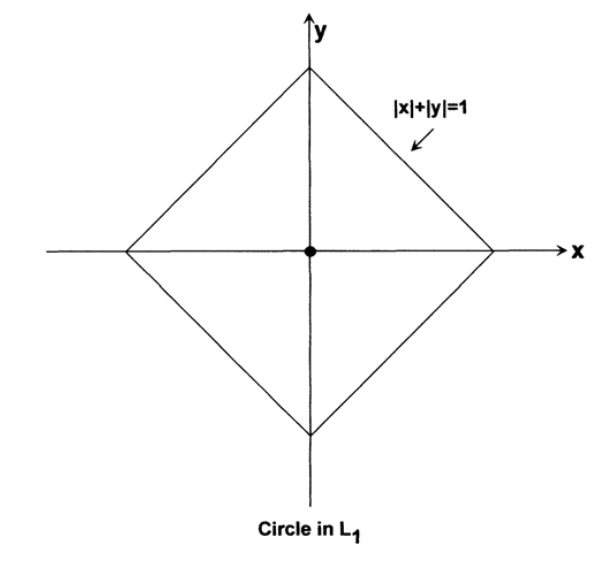
Рис. 9.V

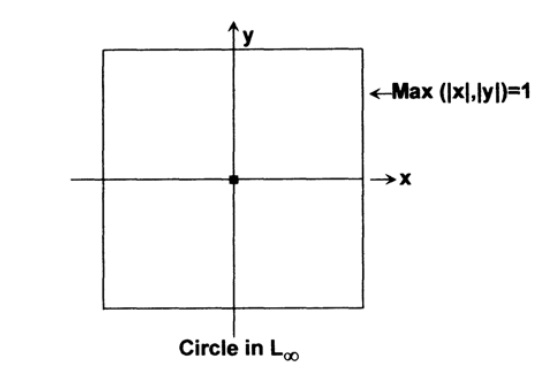
Рис. 9.VI

Оставляю вам проверить, что три метрики L∞, L2 и L1 (Чебышева, Пифагора и Хэмминга) все удовлетворяют этим условиям.

Правда в том, что в сложном проектировании для различных координат мы можем использовать любую из этих метрик, перемешанных вместе, так что пространство проектирование это не целостная картинка, а смесь кусочков и частей. L2 метрика очевидно связана с наименьшими квадратами, а остальные две L∞ и L1 более похожи на сравнения. При сравнениях в реальной жизни вы обычно используете либо максимальную разность L∞ в какой-то одной характеристике как достаточное условие для различения двух предметов, или иногда, как в строках бит, это количество несовпадений, которое существенно, а сумма квадратов не подходит, значит, что используется L1 метрика. Это в большей степени истинно для идентификации шаблонов в ИИ.

К сожалению, хотя все описанное выше истинно, оно редко открывается вам. Никто никогда не говорил мне об этом! Мне понадобится многое из результатов в последующих главах, но вообще говоря после этой демонстрации вы должны быть лучше подготовлены чем были до этого для сложного проектирования и для тщательного анализа пространства, в котором проектирование проводится, как я попытался сделать. Беспорядок, в основном то место где появляется проектирование, и вы должны найти приемлемое решение.

Так как L1 и L∞ не общеизвестны, позвольте несколько замечаний о трех метриках. L2 естественная функция расстояния для использования в физических и геометрических случаях, включая извлечение данных из физических измерений. Поэтому в физике вы повсюду найдете L2. Но когда предмет касается интеллектуальных суждений, остальные 2 метрики более подходят, хотя это медленно воспринимается, поэтому мы часто видим частое использование оценки хи-квадрат, которая очевидно является мерой L2, там где должны использоваться другие более подходящие оценки.

Продолжение следует…

Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

© Habrahabr.ru