[Перевод] Решение уравнения тетраэдра доказано спустя десятки лет после компьютерного поиска
Как четыре математика решили вопрос о базовых геометрических фигурах, создав полный список тетраэдров с рациональными углами при помощи методов теории чисел.
Все 59 тетраэдров с рациональными двугранными углами можно рассмотреть с разных сторон по ссылке.
Тетраэдр — это простейшая трехмерная фигура с плоскими сторонами. Его основные свойства озадачивали пытливые умы еще во времена Платона и Аристотеля. А в ноябре 2020 было опубликовано окончательное доказательство, в котором достоверно идентифицированы все существующие особые тетраэдры. В этой работе математики отвечают на вопрос о древней фигуре благодаря передовым технологиям, которые дают возможность использовать новый метод поиска решений определенных уравнений.
«Это идеализированные математические объекты, которые будут с нами всегда, и теперь мы знаем их все», — утверждает Мартин Вайсман из Калифорнийского университета в городе Санта-Круз.
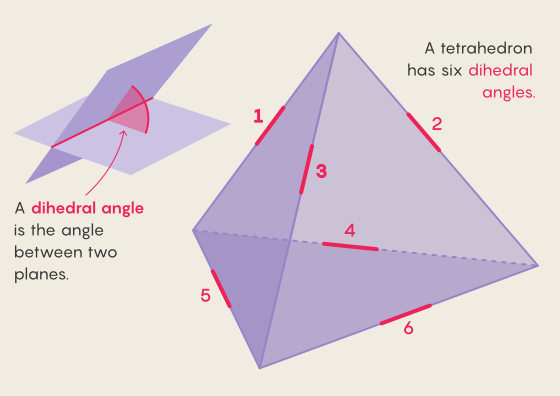
Тетраэдр имеет треугольное основание и три треугольные стороны, образующие пирамиду. Пары граней соприкасаются по краям, образуя шесть двугранных углов.
Новое доказательство определяет все варианты конфигурации тетраэдра, где каждый из шести двугранных углов имеет рациональные значения, а это означает, что каждый из них можно записать в виде дроби. Оно устанавливает, что существует ровно 59 отдельных примеров, а также 2 бесконечных семейства тетраэдров, удовлетворяющих этому условию.
На самом деле, эти тетраэдры математики открыли несколько десятилетий назад с помощью методов компьютерного поиска, но они не знали, существуют ли какие-нибудь еще. В более широком смысле, они не понимали, как доказать, что нет других подобных тетраэдров.
«Они были найдены еще в 1990-х годах, но только в 2020 году мы смогли доказать, что список исчерпывающий», — сказал Киран Кедлая, математик из Калифорнийского университета в Сан-Диего. Кедлая является соавтором доказательства вместе с Александром Колпаковым из Университета Невшателя в Швейцарии, Бьорном Пуненом из Массачусетского технологического института и Майклом Рубинштейном из Университета Ватерлоо.
Сэмюэл Веласко / Quanta Magazine
Проблема классификации тетраэдров с рациональными двугранными углами может показаться простой, но для ее решения потребовались годы накопленных математических знаний, а также вычислительные мощности, которые не были доступны даже десять лет назад.
«Невозможно получить такой результат, просто играя с ручкой и бумагой. Они разработали очень сложные методы », — считает Марджори Сенешал из Колледжа Смит.
В 30-страничном доказательстве почти нет рисунков. Вместо этого логика строится на решении полиномиального уравнения, в котором коэффициенты и переменные возведены в степень, например y = 3×2 + 6. Конечно, уравнение, рассматриваемое в доказательстве, намного сложнее.
«Большая часть работы основана на теории чисел, но на ее поверхности лежит геометрия», — говорит Кедлая.
Связь между геометрией и теорией чисел дала математикам зацепку, но им пришлось немало потрудиться, чтобы развить эту мысль, потому что найти специальные решения сложных уравнений и доказать, что вы нашли их все, очень сложно. Математики не знают, как это сделать для большинства уравнений.
«Не существует универсального метода, который бы всегда работал. Вы почти никогда не сможете решить уравнение», — утверждает Питер Сарнак из Института перспективных исследований.
Вот только в этом случае у математиков все получилось! Обнаружив новый метод поиска решений полиномиальных уравнений, они ответили на основной вопрос о геометрических фигурах и, возможно, упростили поиск решений для других уравнений в будущем.
Тестирование тетраэдров
Вопрос об определении всех тетраэдров с рациональными двугранными углами (рациональные тетраэдры) впервые был официально сформулирован Джоном Конвеем и Антонией Джонс в статье 1976 года.
Они хотели найти тетраэдры, которые можно можно было бы разрезать и собрать в куб того же объема, — свойство, известное как равносоставленность. В своей работе они развивали рассуждения, восходящие к 1900 году, когда Давид Гильберт предложил 23 проблемы, которыми руководствовались математические исследования в 20 веке. Его третья проблема связана со следующим вопросом: являются ли пары трехмерных фигур равного объема равносоставленными. Вскоре было доказано, что это не так, но оказалось, что все рациональные тетраэдры конгруэнтны кубу.
«Конвэй и Джонс задавали вопрос о рациональных тетраэдрах как о частном случае гораздо более сложного вопроса классификации тетраэдров», — сказал Кедлая.
Это идеализированные математические объекты, которые будут с нами всегда.Мартин Вайсман, Калифорнийский университет, Санта-Круз.
Они смогли составить набросок метода поиска этих тетраэдров: решение конкретного полиномиального уравнения. Их уравнение содержит шесть переменных, соответствующих шести двугранным углам тетраэдра, и имеет 105 членов, отражающих сложную связь двугранных углов тетраэдра друг с другом. Для сравнения представьте треугольник, три его внутренних угла связаны в рамках простого многочлена, состоящего всего из трех членов: a + b + c = 180 градусов.
Полиномиальное уравнение, идентифицированное Конвеем и Джонсом, также имеет бесконечно много решений, которые соответствуют бесконечным вариантам конфигурации возможных тетраэдров. Конвей и Джонс сказали, что для определения тетраэдров со всеми рациональными двугранными углами математикам нужно найти специальный класс решений уравнения, которые бы точно соответствовали рациональным тетраэдрам.
Сами они не знали, как найти решения, но были уверены, что это можно сделать: «Вполне вероятно, что обычный тетраэдр… чьи двугранные углы рациональны, можно найти с помощью наших методов».
Более чем 40 лет спустя четыре математика подтвердили их предположение.
Корни из единицы
Стратегия Конвея и Джонса довольно распространена среди математиков, которые часто ищут специальные типы решений при изучении полиномиальных уравнений. Это могут быть решения в виде целых или рациональных чисел. Или, как в данном случае, это могут быть решения с элегантным названием «корни из единицы».
Большинство корней из единицы не появляются на обычной числовой прямой. Вместо этого они находятся среди комплексных чисел, таких как 3 + 4i, которые имеют действительную часть (3) и мнимую часть (4). Корни из единицы служат решениями полиномиальных уравнений и обладают особым алгебраическим свойством: при возведении их в определенную степень получается 1. К тому же, у них изящное геометрическое представление: все они лежат на единичной окружности в комплексной плоскости.
Чтобы решить полиномиальное уравнение Конвея-Джонса, необходимо присвоить комплексные числа всем шести переменным, чтобы уравнение из 105 членов было истинным. Переменные не представляют собственно измерения углов в буквальном смысле, а заменяют комплексные числа, связанные с косинусами углов. Конвей и Джонс заметили, что рациональные тетраэдры будут соответствовать решениям многочлена, в котором все переменные являются корнями из единицы.
«Шесть углов становятся шестью точками на единичной окружности, и эти комплексные числа нужны, чтобы удовлетворить полиномиальное уравнение», — сказал Вайсман.

Сэмюэл Веласко / Quanta Magazine
Однако знание этого соответствия не так полезно, как могло показаться. Найти решения — это одно. А доказать, что вы нашли их все, — это совершенно другая и гораздо более сложная задача.
В 1995 году два автора новой работы, Пунен и Рубинштейн, фактически нашли все тетраэдры с рациональными двугранными углами, как оказалось в итоге. По сути, они угадали способ их поиска, подставив в уравнение комбинации из шести рациональных чисел.
«Можно просто попробовать взять шесть рациональных чисел и подставить их в уравнение», — сказал Пунен. «Проблема в том, что этот способ позволяет найти только решения. Но он не дает понять, все ли возможные варианты найдены».
Поиск каждого решения
В своей новой работе четверо математиков доказали, что список тетраэдров с рациональными углами, найденных Пуненом и Рубинштейном 25 лет назад, был полным и открытия других примеров не будет.
Их сотрудничество началось в марте 2020 года после того, как Пунен услышал на одном выступлении о связанной с этим работе Кедлаи в соавторстве другим математиком. Они искали корни из единицы другого многочлена, чтобы решить еще один вопрос классификации. Пунен сразу понял, что это имеет отношение к его предыдущему незавершенному исследованию тетраэдров.
«Бьорна очень заинтересовала моя работа», — сказал Кедлая. «Он сказал: 'Подождите, это именно то, что мне было нужно в 1990-е'».
Бьорн Пунен написал Кирану Кедлае письмо, в котором описал проблему поиска рациональных тетраэдров. Его краткое письмо заканчивалось на оптимистичной ноте. «Я довольно далеко продвинулся в этом вопросе еще в 1990-х [с Майклом Рубинштейном], и я думаю, что его возможно завершить, выполнив большую работу много усилий человека и компьютера.
В 2020 году Киран Кедлая, Майкл Рубинштейн, Бьорн Пунен и Александр Колпаков изобрели новый способ решения уравнений и при этом нашли все рациональные тетраэдры.
После этого письма Кедлая обратился к Колпакову, который также применял корни из единицы для классификации типов геометрических фигур. В то же время Пунен связался со своим тогдашним соавтором Рубинштейном. Создав команду, они быстро приступили к работе.
«Мы организовывали довольно регулярные встречи, наверное, по два часа в неделю в течение нескольких месяцев», — сказал Кедлая. И когда они начали составлять полный список корней из единицы для многочлена Конвея-Джонса, у них было очень широкое представление о том, где их искать.
Они знали, что решения должны находиться ниже какого-то очень большого числа, верхней границы. Но граница была настолько велика, что и речи не было о том, чтобы изучить все возможности ниже нее.
«Эти границы с шестью переменными просто ужасают. Без принципиально новых идей решение этой проблемы находится за гранью возможного», — сказал Сарнак.
Четыре математика сделали уравнение решаемым благодаря двум основным нововведениям.
Во-первых, они снизили верхнюю границу. В своей новой статье они доказали, что одно сложное полиномиальное уравнение, представляющее тетраэдры, само может быть представлено в виде нескольких более простых многочленов.
«Мы переходим от одного уравнения с шестью переменными к набору сотен более простых уравнений», — сказал Кедлая.
Они доказали, что все корни из единицы этих более простых многочленов лежат ниже верхней границы, которая гораздо меньше обширной и неисследованной верхней границы, связанной с более сложным многочленом. Соответствие между более простыми уравнениями и сложным означает, что обнаружение корней из единицы для первых приведет к корням из единицы для последнего. К сожалению, даже этот меньший интервал все еще был слишком большим, чтобы они исследовать все возможные варианты.
Невозможно получить такой результат, просто играя с ручкой и бумагой.Марджори Сенешал, Колледж Смит
Второе нововведение авторов состояло в разработке умного способа поиска на этом меньшем интервале. Они знали, что решения имеют определенную симметричную структуру, а значит, при наличии решения в одной части интервала, должно существовать решение и в другой части интервала.
Это позволило им разработать новые алгоритмы, которые использовали эту структуру для более эффективного поиска. К тому же, они использовали эти алгоритмы на гораздо более мощных компьютерах, чем те, что были в распоряжении Конвея и Джонса, когда они впервые предложили использовать корни из единицы для решения проблемы.
«Оказывается, нам пришлось немного модернизировать стратегию [Конвея и Джонса], при помощи 40 лет дополнительных знаний и более мощных компьютеров», — сказал Кедлая.
Новые алгоритмы проверили все возможные комбинации решений в более узком интервале. На основе этого исчерпывающего окончательного поиска, авторы наконец доказали, что существует всего 59 отдельных примеров тетраэдров с рациональными двугранными углами и два бесконечных семейства тетраэдров (именно те, с которыми Пунен и Рубинштейн столкнулись десятилетиями ранее). Тетраэдры в каждом бесконечном семействе различаются одним параметром, предлагая бесконечные варианты увеличения размера одних углов и уменьшения других, сохраняя при этом все двугранные углы рациональными.
В этом исследовании каждый найдет что-то для себя.
Для математиков, заинтересованных в выявлении корней из единицы полиномиальных уравнений, в статье предлагается новый удобный способ их нахождения. В частности, методы, использованные авторами для приведения сложного многочлена Конвея-Джонса ко многим более простым многочленам, вероятно, будут применяться к другим сложным полиномиальным уравнениям, которые не могут быть решены напрямую.
«Эта работа предполагает, что многие другие проблемы, которые казались нерешаемыми, возможно, могут быть решены с помощью таких идей», — сказал Сарнак.
А для тех математиков и всех остальных, кому нравится завершенность, статья дает новый и совершенный ответ: здесь находятся все тетраэдры, о которых только можно мечтать.
«Это прекрасное достижение», — отметил Сарнак.
