[Перевод] Пишем игру от первого лица в 2КБ на Rust10.03.2023 11:16

Введение

Поначалу кажется, что создать игру от первого лица без движка или графического API практические невозможно. В этом посте я расскажу, как это сделать при помощи алгоритма под названием ray casting.

Моя цель — показать, что сложную задачу можно разбить на более простые части, и если я всё сделаю правильно, то у вас появится ощущение, что вы сами открыли, как работает игра.

Для начала разберёмся, как работает алгоритм, а затем построчно напишем его. Затем мы пересмотрим код, добавим несколько возможностей и оптимизируем его размер. Я постарался сделать пост максимально доступным и дружелюбным, но вам поможет приличное знание программирования, Rust и основ геометрии.
Вот краткое превью того, что мы будем делать

Если вы просто хотите посмотреть исходный код, то перейдите в репозиторий на Github.

Мои первые опыты с подобными играми (хотя в то время я об этом ещё не знал) начались в средней школе с игр наподобие zDoom на калькуляторе. zDoom (хотя и не был особо интересным) казался мне удивительным, потому что мог создавать своего рода иллюзию глубины и перспективы, на что, по моему мнению, были способны только «настоящие» игры.

zDoom был всего лишь имитацией настоящего Doom, на самом деле, он гораздо ближе к предшественнику Doom под названием Wolfenstein 3D.

Wolfenstein 3D

Знаменитая игра Wolfenstein 3D, выпущенная в 1992 году, была одним из первых 3D-шутеров от первого лица для потребительских ПК. В те времена у компьютеров не было аппаратного 3D-ускорения, не говоря уж об специальных графических картах, так как же игра была устроена?

Скриншот Wolfenstein 3D

Ну, на самом деле нужно было сказать «псевдо-3D», потому что ни одна часть игры не работала в трёх измерениях. Основой игры был алгоритм под названием ray casting (рейкастинг, метод «бросания лучей») — процесс проецирования 2D-игры в 3D-перспективу. (В этом посте я ради краткости называю термином ray casting конкретный алгоритм рейкастинга, используемый в играх наподобие Wolfenstein 3D. Это немного неточно, поскольку в области графики термин ray casting имеет более общее значение. См. статью в Википедии.)

Все объекты игры располагались в простых координатах x и y карты и не могли перемещаться по вертикали. На момент выпуска игры это казалось мне неважным, однако сегодня она выглядит сильно устаревшей. Игрок не мог смотреть вверх или вниз, не мог ползать и прыгать.

Вид сверху на первый уровень Wolfenstein 3D

Кроме того, все уровни состояли из единственных этажей здания без окон. Все стены были идеально прямыми, а углы располагались с равномерными интервалами (что сегодня совершенно неприемлемо). Эти аспекты дизайна были использованы из-за неотъемлемых ограничений, свойственных данному простому алгоритму ray-casting.

Алгоритм

Основы

На самом фундаментальном уровне ray casting основан на простом факте: удалённые от нас объекты выглядят меньше, а близкие — больше. Ray casting использует это наблюдение, отрисовывая далёкие от игрока стены с меньшей высотой, а близкие к нему — с большей.

Даже эта простая идея создаёт убедительную иллюзию глубины и позволяет нам перемещать игрока, как будто он рендерится в реальном 3D.

Ray casting трассирует путь от игрока до ближайшей стены для каждого столбца окна обзора игрока. Затем он записывает расстояния каждого пути и преобразует их в высоту стены и рисует её на экране в виде вертикальной линии.

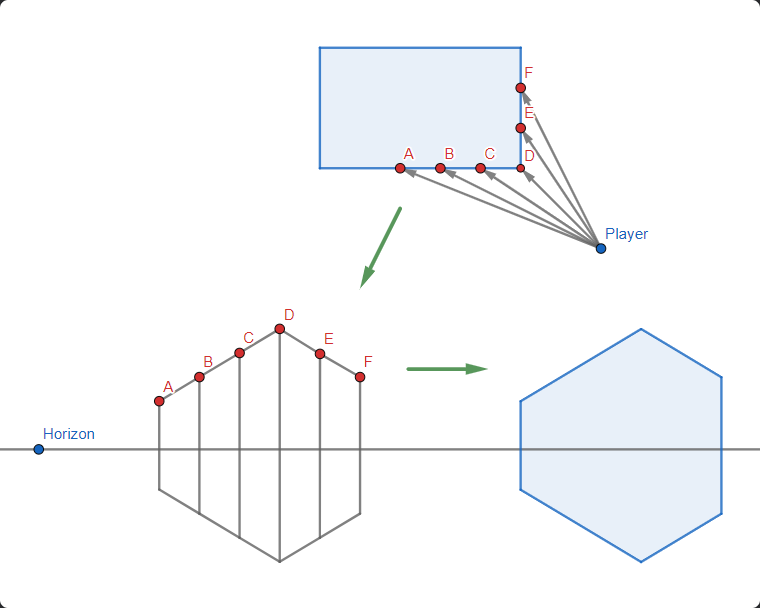
Из этого описания алгоритма ray casting мы можем понять, что нам нужно делать:

• Испустить луч из игрока и остановиться на ближайшей стене
• Вычислить расстояние от игрока до ближайшей стены
• Преобразовать это расстояние в высоту стены и отрисовать её на экране
• Повторять для каждого столбца экрана

Углубляемся дальше

Самое сложное — это пункт «испустить луч из игрока и остановиться на ближайшей стене». В теории кажется простым, но на практике это может быть довольно трудно. Если бы мне пришлось самостоятельно придумывать реализацию
ray casting, то как бы я подошёл к решению этой задачи?

Проблема пересечения

Первым делом большинство людей скорее всего бы предложило многократно продлевать луч на небольшое расстояние и останавливаться, когда он столкнётся со стеной. [«Продление луча» — это не совсем точное использование понятия, вернее было бы назвать его в этой ситуации «вектором», однако «луч» звучит лучше, к тому же это слово используется в названии «ray casting».] Но это проблематично, поскольку продлевая луч, мы можем перескочить через стену. А если луч столкнётся со стеной, то это будет давать очень низкую точность, поскольку он не будет знать точно, где началась стена.

Наивное решение

Нам нужно каким-то образом гарантировать, что луч пересечётся со стеной и остановится ровно на границе стены. В мире математики это можно было бы сделать, продлевая луч на бесконечно малое расстояние бесконечно много раз. К сожалению, мы находимся не в мире математики и не можем этого сделать.

Решением этой проблемы, как можно было понять из предыдущего описания, станет привязка всех стен к сетке. Если мы знаем, что стены встречаются с предсказуемыми интервалами, то можно каждый раз вычислять надёжное расстояние, на которое нужно продлевать луч.

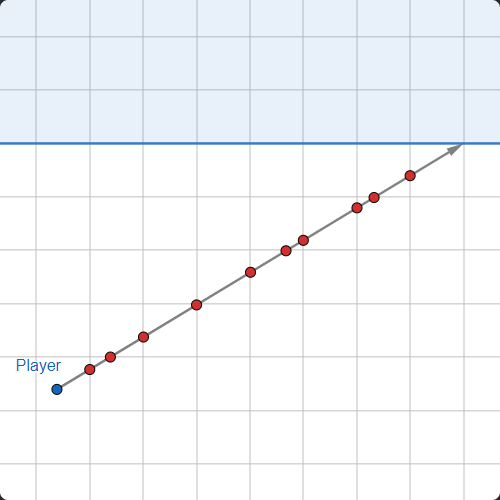
Заметили паттерн?

Но как луч доскочит до стены?

Если взять бумагу в клетку и начать рисовать линии между игроком и разными стенами, то вы заметите определённые паттерны. «Продления» лучей до стен на горизонтальных линиях сетки имеют общую ширину, а «продления» лучей, попадающие на стены на вертикальных линиях сетки, имеют одинаковую высоту.

Продлив луч до первой линии сетки, мы можем вычислить эти общие «ширины продлений» и «высоты продлений». Затем мы многократно будем продлевать луч на эти ширины и высоты, чтобы получить первую «вертикальную стену» и «горизонтальную стену», и используем меньшее из двух расстояний.

Наверно, это всё слишком сложно, поэтому объясню чуть подробнее.

Горизонтальные пересечения

Вот пример того, что происходит, когда игрок смотрит на «горизонтальную стену». [В оригинале статьи схема интерактивна.]

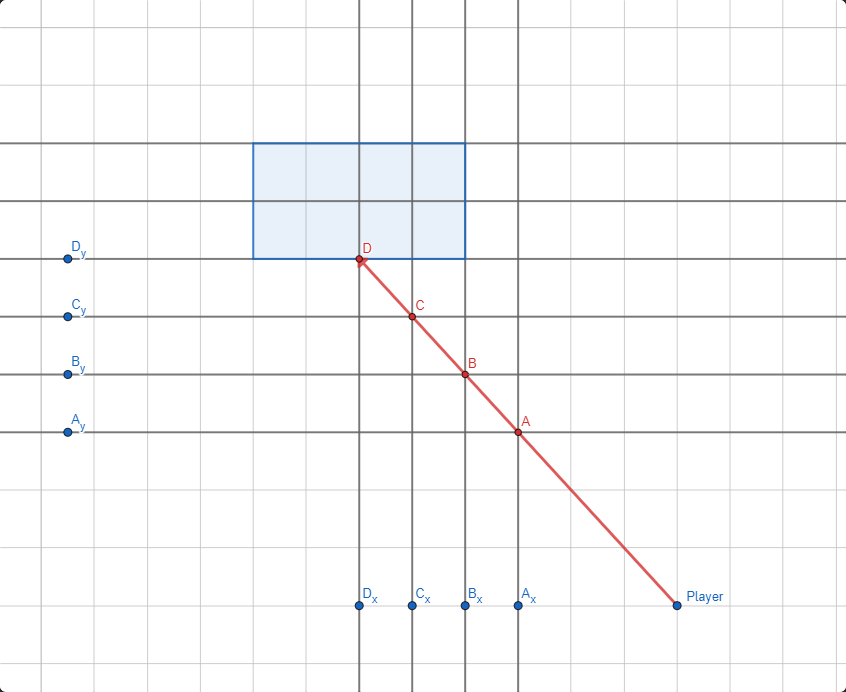
При перемещениях игрока меняется только ширина между продлениями луча.

Во взаимодействиях с горизонтальными стенами высота между «продлениями» всегда равна единице, а ширину между «продлениями» можно вычислить по углу луча. Он всегда движется вверх или вниз ровно на единицу и вправо или влево на величину, определяемую углом луча.

Это видно по схеме: ширина между  и  такая же, как ширина между  и , а разность высот между всеми точками всегда равна единице.

При помощи простой тригонометрии мы можем найти ширину между горизонтальными пересечениями сетки из угла игрока. Я сэкономлю вам время и просто дам формулу

Вертикальные пересечения

Вот ещё одна схема (в оригинале статьи интерактивная) пересечения луча с «вертикальной стеной».

Здесь высота между продлениями меняется, а ширина остаётся той же

Вертикальные пересечения сетки такие же, как и горизонтальные, только повёрнутые на 90°. В вертикальных пересечениях ширина между «продлениями луча» постоянна, а высота воссоздаётся по углу луча. Как и ранее, я пропущу вывод и покажу только формулы.

Подведём итог

Теперь, когда мы достаточно чётко знаем, как это сделать, превратим это в более подробный поэтапный список, который наша программа будет выполнять в каждом кадре.

Для каждого столбца на экране:

1. Найти угол для луча из угла игрока и поля его зрения.
2. Определить расстояние до ближайшей стены, с которой пересекается луч:
   • Получить первую «горизонтальную» стену, с которой пересекается луч.
   • Получить первую «вертикальную» стену, с которой пересекается луч.
   • Вычислить расстояние до ближайшей из этих двух стены.
3. Преобразовать это расстояние в высоту стены на экране, а затем отрисовать её.

Реализация

Теперь, когда мы знаем, как внутри устроен алгоритм, можно написать программу, которая реализует его с использованием WASM-4.

Постойте, а почему WASM-4? Официальный ответ: потому что наша программа должна как-то принимать пользовательский ввод и выполнять отрисовку на экране. Реальный ответ: он мне сильно нравится.

WASM-4 — это крошечный игровой движок, выполняющий файлы WebAssembly (.wasm). Большинство компилируемых языков программирования (C, C++, Rust, Zig и так далее) можно компилировать в WebAssembly, то есть игры для WASM-4 можно писать на любом из этих языков! WASM-4 чрезвычайно минималистичен,»4» в названии WASM-4 означает, что на экране можно одновременно отрисовывать только четыре цвета.

Я воспользуюсь Rust, а вы можете писать игру на любом языке, который компилируется в WebAssembly. Если вам ближе JavaScript, то рекомендую AssemblyScript.

WASM-4 позволит нам создавать крошечные игры, потому что предоставляет для творчества простую платформу. WASM-4 занимается работой с окнами, рендерингом графики и вводом с геймпада, а всё остальное предстоит сделать нам.

Вот спецификации «вымышленной консоли» WASM-4 с её сайта:

• Экран: 160×160 пикселей, 4 настраиваемых цвета, обновляется с частотой 60 Гц.
• Память: 64 КБ линейной ОЗУ, ввод-вывод с отображением в память, сохранение состояний.
• Максимальный размер картриджа: 64 КБ.
• Ввод: клавиатура, мышь, сенсорный экран, до четырёх геймпадов.
• Звук: 2 канала импульсных волн, 1 канал треугольных волн, 1 канал шума.
• Дисковый накопитель: 1024 байта.

Если вы немного разбираетесь в компьютерном «железе», то понимаете насколько невероятно жёсткие это ограничения для игры. Однако мне было интересно увидеть, сколько всего можно уместить в 160×160 пикселей, 4 цвета и 64 КБ на диске. Если вам любопытно, что с такими ограничениями способны делать люди, зайдите на сайт WASM-4, там есть впечатляющие игры (в том числе и лётный симулятор!).

Вероятно, в будущем я напишу более подробный пост о WASM-4, но пока такого объяснения будет достаточно. Для запуска игр на WASM-4 достаточно скачать и установить минимальную среду исполнения.

Подготовка проекта

Так как WASM-4 выполняет файлы WebAssembly, нам нужно сконфигурировать проект, чтобы создать такой файл.

$ cargo new raycaster --lib && cd raycaster

Добавим это в Cargo.toml:

[lib]
crate-type = ["cdylib"]

[profile.release]
opt-level = "z"
lto = true
codegen-units = 1
strip = true
panic = "abort"

[dependencies]
libm = "0.2"

Мы можем сообщить cargo, что хотим создать динамическую библиотеку в стиле C (.wasm) и оптимизировать двоичный файл для минимизации размера. Также импортируем библиотеку libm, которая предоставит нам no_std-реализации нужных нам функций наподобие sin, tan и floor (подробнее об этом позже).

В файл конфигурации крейта .cargo/config.toml добавим следующее:

[build]
target = "wasm32-unknown-unknown"

[target.wasm32-unknown-unknown]
rustflags = [
    "-C", "link-arg=--import-memory",
    "-C", "link-arg=--initial-memory=65536",
    "-C", "link-arg=--max-memory=65536",
    "-C", "link-arg=-zstack-size=14752",
]

Это прикажет cargo по умолчанию использовать WebAssembly и передать rustc флаги, приказывающие программе зарезервировать для игры память.

Теперь давайте добавим в файл исходников src/lib.rs простой бойлерплейт:

#![no_std]

use core::{arch::wasm32, panic::PanicInfo};

const GAMEPAD1: *const u8 = 0x16 as *const u8;

const BUTTON_LEFT: u8 = 16;  // 00010000
const BUTTON_RIGHT: u8 = 32; // 00100000
const BUTTON_UP: u8 = 64;    // 01000000
const BUTTON_DOWN: u8 = 128; // 10000000

extern "C" {
    fn vline(x: i32, y: i32, len: u32);
}

#[panic_handler]
fn phandler(_: &PanicInfo<'_>) -> ! {
    wasm32::unreachable();
}

#[no_mangle]
unsafe fn update() {
    if *GAMEPAD1 & BUTTON_UP != 0 {
        vline(80, 20, 120);
    }
}

Вот небольшое объяснение кода для тех, кто незнаком с Rust или WASM-4:

• #![no_std] запрещает программе выполнять доступ к стандартной библиотеке Rust. Это необходимо почти для всех игр на WASM-4, поскольку стандартная библиотека велика, из-за чего наша игра может занять больше 64 КБ.
• GAMEPAD1 — это указатель на текущее состояние первого геймпада (в нашем случае на клавиши со стрелками). Среда исполнения в каждом кадре будет записывать в эту область памяти состояние геймпада (клавиатуры).
• Константы с BUTTON_LEFT по BUTTON_DOWN описывают биты геймпада, описывающие каждую кнопку. Можно использовать их для проверки того, сообщает ли GAMEPAD1 о нажатии кнопки; именно это мы будем делать, вызывая *GAMEPAD1 & BUTTON_UP != 0.
• extern "C" fn vline привязывает нашу игру к внешней функции vline, предоставляемой нам движком WASM-4.
  vline отрисовывает вертикальную линию в окне по координатам x, y и протягивает её вниз на len пикселей.
• #[panic_handler] fn phandler — это небольшой фрагмент бойлерплейта, который должен реализовать Rust, если мы решаем использовать #![no_std]. Эта функция будет выполняться при панике программы. Так как WASM-4 настолько жёстко ограниченная среда, единственное, что мы можем сделать — это вызвать wasm32::unreachable().
• unsafe fn update — это основная точка входа нашей программы, WASM-4 вызывает эту функцию в каждом кадре.

Для компиляции игры мы можем собрать её как любой другой крейт:

$ cargo build --release

А для её запуска можно использовать w4 run-native:

$ w4 run-native target/wasm32-unknown-unknown/release/raycaster.wasm

Запустится пустое окно, и если мы нажмём на стрелку вверх на клавиатуре, появится вертикальная линия в палитре Gameboy.

Получилось!

В ситуациях с подобными командами, которые мы будем вызывать часто, я люблю помещать их в простой Makefile, чтобы нам не пришлось вводить команды заново или слишком часто использовать стрелку вверх. После этого для сборки и запуска программы остаётся ввести make run.

all:
    cargo build --release

run: all
    w4 run-native target/wasm32-unknown-unknown/release/raycaster.wasm

Отлично, рабочий процесс готов, мы можем приступать к написанию игры.

Хранение карты

Проще всего хранить карту в сетке, состоящей из стен и «не-стен». Один из способов заключается в сохранении карты в виде [[bool; WIDTH]; HEIGHT] и в выполнении доступа к ней при помощи map[][]. Подобное хранение карты не будет особо изящным решением, потому что нам придётся вводить каждую ячейку по отдельности как true или false.

Так как булево значение (стена и «не-стена») можно представить одним битом, для описания карты можно использовать биты внутри числа: [u16; HEIGHT]. В таком случае [u16; HEIGHT] может обозначать карту шириной 16 ячеек и произвольной выбранной нами высоты. При помощи синтаксиса целочисленных литералов Rust мы можем достаточно просто представить нашу карту, записывая 1 там, где должна быть стена, и 0, не должна быть «не-стена»:

const MAP: [u16; 8] = [
    0b1111111111111111,
    0b1000001010000101,
    0b1011100000110101,
    0b1000111010010001,
    0b1010001011110111,
    0b1011101001100001,
    0b1000100000001101,
    0b1111111111111111,
];

При таком способе хранения карты к ней сложнее получать доступ. Для этого нужно написать функцию, которая сначала индексирует строку в конкретный столбец при помощи маскирования, а затем сдвигает строку. Пост и так получился длинным, так что ради экономии времени я не буду вдаваться в подробности о том, как в этой функции работают битовые операции поиска координаты X.

/// Проверяем, содержит ли карта стену в точке.
fn point_in_wall(x: f32, y: f32) -> bool {
    match MAP.get(y as usize) {
        Some(line) => (line & (0b1 << x as usize)) != 0,
        None => true,
    }
}

Так как наша карта окружена стенами, то если вызывающий эту функцию передаёт координату вне пределов карты, можно безопасно сообщить, что стена есть.

Стоит также заметить, что в point_in_wall ось Y «перевёрнута», то есть находится наверху. Это не только быстрее, но и отражает систему координат, которая чаще всего используется в ПО.

Хранение состояния игры

Во время выполнения программы карта остаётся неизменной, меняются позиция и угол игрока. Так как WASM-4 вызывает update в каждом кадре, единственный способ хранения состояния игры между кадрами — это что-то типа static mut языка Rust. Так как static mut является unsafe, нам нужно объединить логику игры и состояние в единую struct, чтобы минимизировать количество случаев модификации состояния через static mut.

Для описания окна просмотра игрока достаточно всего трёх переменных: позиций X и Y, а также угла обзора.

struct State {
    player_x: f32,
    player_y: f32,
    player_angle: f32,
}

Теперь поместим State в static mut:

static mut STATE: State = State {
    player_x: 1.5,
    player_y: 1.5,
    player_angle: 0.0,
};

Изначально и player_x, и player_y имеют значение 1.5, чтобы игрок всегда начинал с центра ячейки, а не внутри стены.

unsafe-поведением является не только доступ к State, но и большинство взаимодействий с WASM-4 (разыменование сырых указателей, вызов внешних функций и так далее).

Для незнакомых с Rust скажу, что unsafe — это ключевое слово/блок, который мы передаём компилятору, когда нам нужно обойти гарантии безопасности памяти. Использование unsafe говорит компилятору Rust: «Я знаю, что делаю, не надоедай мне с этим». Проблема в том, что часто мы не знаем, что делаем. Из-за этого стоит использовать unsafe по минимуму.

Если мы объединим unsafe-поведение в fn update, а игровую логику в State, то изолируем состояние и придадим программе структуру. Это даёт нам достаточно чёткую линию: unsafe (небезопасный) ввод-вывод при помощи WASM-4 в fn update, безопасная игровая логика в State.

Перемещение персонажа

Одна из простейших частей этой игры — перемещение персонажа. Так как доступ к STATE снаружи является unsafe, давайте создадим внутри State метод для перемещения персонажа и в каждом кадре будем передавать ему ввод.

impl State {
    /// перемещение персонажа
    pub fn update(&mut self, up: bool, down: bool, left: bool, right: bool) {
        // сохраняем текущую позицию на случай, если она пригодится позже
        let previous_position = (self.player_x, self.player_y);

        if up {
            self.player_x += cosf(self.player_angle) * STEP_SIZE;
            self.player_y += -sinf(self.player_angle) * STEP_SIZE;
        }

        if down {
            self.player_x -= cosf(self.player_angle) * STEP_SIZE;
            self.player_y -= -sinf(self.player_angle) * STEP_SIZE;
        }

        if right {
            self.player_angle -= STEP_SIZE;
        }

        if left {
            self.player_angle += STEP_SIZE;
        }

        // если перемещение в этом кадре помещает нас в стену, просто откатываем его
        if point_in_wall(self.player_x, self.player_y) {
            (self.player_x, self.player_y) = previous_position;
        }
    } 
}

Если вы когда-нибудь перемещали персонажа в игре и знаете основы тригонометрии, то код покажется вам знакомым. Обратите внимание, что вызовы sinf отрицательны, потому что ось Y перевёрнута.

Если игрок просит нас переместить персонажа вперёд или назад, мы изменяем позиции x и y на основании значений cosf и sinf, умноженных на константу STEP_SIZE.

Только для вас я укажу волшебное число, которое здесь неплохо подходит. При желании вы сможете его изменить:

const STEP_SIZE: f32 = 0.045;

Последнее, что нужно сделать для работы этой функции — импортировать cosf и sinf из libm.

use libm::{cosf, sinf};

Почему sinf/cosf, а не sin/cos? Этот принцип именования взят из libm языка C, где sin/cos работают с double, а sinf/cosf с float. В реализации libm языка Rust это значит fn cos(x: f64) -> f64 и fn cosf(x: f32) -> f32. Мы используем f32, а не f64, потому что это экономит место и нам не нужна такая точность.

Последнее, что нам нужно сделать — разумеется, вызвать новый State::update!

Горизонтальные пересечения

Прежде чем отрисовать стены на экране, нужно реализовать ядро нашего алгоритма: проверки горизонтальных и вертикальных пересечений.

Сначала нужно расширить предыдущий оператор импорта libm:

use libm::{ceilf, cosf, fabsf, floorf, sinf, sqrtf, tanf};

При помощи libm::sqrtf мы можем создать функцию расстояния :

fn distance(a: f32, b: f32) -> f32 {
    sqrtf((a * a) + (b * b))
}

Далее импортируем полезные константы основной библиотеки для  и :

use core::f32::consts::{PI, FRAC_PI_2};

Так как нам нужно получать доступ к углу и позиции игрока, давайте создадим внутри State метод horizontal_intersection. Это будет самая сложная функция из тех, которые мы писали, но, по сути, она отражает уже описанный мной алгоритм, так что в этом случае я оставлю свои комментарии внутри кода.

impl State {
    /// Возвращает ближайшую стену, с которой пересекается луч на горизонтальной линии сетки.
    fn horizontal_intersection(&self, angle: f32) -> f32 {
        // Это сообщает нам, "смотрит" ли угол вверх,
        // вне зависимости от величины угла.
        let up = fabsf(floorf(angle / PI) % 2.0) != 0.0;

        // first_y и first_x - первые пересечения сетки,
        // с которыми пересекается луч.
        let first_y = if up {
            ceilf(self.player_y) - self.player_y
        } else {
            floorf(self.player_y) - self.player_y
        };
        let first_x = -first_y / tanf(angle);

        // dy и dx - это упомянутые выше значения "продления луча".
        let dy = if up { 1.0 } else { -1.0 };
        let dx = -dy / tanf(angle);

        // next_x и next_y - это изменяемые значения, которые отслеживают,
        // насколько далеко луч от игрока.
        let mut next_x = first_x;
        let mut next_y = first_y;

        // Это цикл, в котором луч продляется, пока не столкнётся
        // со стеной. Это не бесконечный цикл, как следует из объяснения,
        // итерация идёт только от 0 до 256.
        //
        // Так сделано, потому что если что-то пойдёт не так
        // и луч никогда не столкнётся со стеной (чего никогда не должно произойти),
        // цикл прервётся и игра продолжит работать.
        for _ in 0..256 {
            // current_x и current_y - это место, где в данный момент луч
            // находится на карте, а next_x и next_y - относительные
            // координаты, current_x и current_y - абсолютные
            // точки.
            let current_x = next_x + self.player_x;
            let current_y = if up {
                next_y + self.player_y
            } else {
                next_y + self.player_y - 1.0
            };

            // Приказываем циклу завершиться, если мы столкнулись со стеной.
            if point_in_wall(current_x, current_y) {
                break;
            }

            // если мы не столкнулись со стеной на этом продлении,
            // прибавляем к текущей позиции dx и dy и продолжаем.
            next_x += dx;
            next_y += dy;
        }

        // возвращаем расстояние от next_x и next_y до игрока.
        distance(next_x, next_y)
    }
}

Вертикальные пересечения

Давайте перед отрисовкой стен также реализуем вертикальные пересечения.

Вы заметите, что эта функция практически идентична предыдущей. Давайте добавим внутрь State метод vertical_intersection, аналогичный horizontal_intersection:

impl State {
    /// Возвращает ближайшую стену, с которой пересекается луч на вертикальной линии сетки.
    fn vertical_intersection(&self, angle: f32) -> f32 {
        // Это сообщает нам, "смотрит" ли угол вверх,
        // вне зависимости от величины угла.
        let right = fabsf(floorf((angle - FRAC_PI_2) / PI) % 2.0) != 0.0;

        // first_y и first_x - первые пересечения сетки,
        // с которыми пересекается луч.
        let first_x = if right {
            ceilf(self.player_x) - self.player_x
        } else {
            floorf(self.player_x) - self.player_x
        };
        let first_y = -tanf(angle) * first_x;

        // dy и dx - это упомянутые выше значения "продления луча".
        let dx = if right { 1.0 } else { -1.0 };
        let dy = dx * -tanf(angle);

        // next_x и next_y - это изменяемые значения, которые отслеживают,
        // насколько далеко луч от игрока.
        let mut next_x = first_x;
        let mut next_y = first_y;

        // Это цикл, в котором луч продляется, пока не столкнётся
        // со стеной. Это не бесконечный цикл, как следует из объяснения,
        // итерация идёт только от 0 до 256.
        //
        // Так сделано, потому что если что-то пойдёт не так
        // и луч никогда не столкнётся со стеной (чего никогда не должно произойти),
        // цикл прервётся и игра продолжит работать.
        for _ in 0..256 {
            // current_x и current_y - это место, где в данный момент луч
            // находится на карте, а next_x и next_y - относительные
            // координаты, current_x и current_y - абсолютные
            // точки.
            let current_x = if right {
                next_x + self.player_x
            } else {
                next_x + self.player_x - 1.0
            };
            let current_y = next_y + self.player_y;

            // Приказываем циклу завершиться, если мы столкнулись со стеной.
            if point_in_wall(current_x, current_y) {
                break;
            }

            // если мы не столкнулись со стеной на этом продлении,
            // прибавляем к текущей позиции dx и dy и продолжаем.
            next_x += dx;
            next_y += dy;
        }

        // возвращаем расстояние от next_x и next_y до игрока.
        distance(next_x, next_y)
    }
}

Получаем окно просмотра

Пока мы не написали ничего, с чем можно было бы взаимодействовать. Точнее, мы можем действовать (перемещать персонажа), но не увидим, как это происходит. Давайте попробуем отрисовывать стены.

Как говорилось в разделе «Подведём итог», нам нужно рисовать вертикальные линии для каждого столбца в окне.

Можно разделить это на две отдельные задачи: получение высот линий и отрисовка их на экране. Почему не делать всё одновременно? Потому что vline является unsafe, поэтому нужно оставить её в fn update.

Давайте сделаем это, определив State::get_view, возвращающий список всех высот стен. Тогда в каждом кадре мы сможем вызывать State::get_view из fn update и отрисовывать все эти вертикальные линии, которые мы только что вычислили.

#[no_mangle]
unsafe fn update() {
    STATE.update(
        *GAMEPAD1 & BUTTON_UP != 0,
        *GAMEPAD1 & BUTTON_DOWN != 0,
        *GAMEPAD1 & BUTTON_LEFT != 0,
        *GAMEPAD1 & BUTTON_RIGHT != 0,
    );

    // обходим каждый столбец на экране и отрисовываем стены в центре.
    for (x, wall_height) in STATE.get_view().iter().enumerate() {
        vline(x as i32, 80 - (wall_height / 2), *wall_height as u32);
    }
}

State::get_view будет обходить каждую вертикальную линию на экране (все 160), вычисляя угловое смещение с точки зрения игрока, а затем находя расстояние до ближайшего горизонтального и вертикального пересечения со стенами на пути луча. Затем он сравнивает два расстояния и превращает меньшее из них в высоту стены.

Знаю, это звучит сложно, поэтому давайте запишем, как это выглядит.

Сначала создадим несколько констант, определяющих перспективу игрока:

const FOV: f32 = PI / 2.7; // Область обзора игрока.
const HALF_FOV: f32 = FOV * 0.5; // Половина области обзора.
const ANGLE_STEP: f32 = FOV / 160.0; // Угол между каждым лучом.
const WALL_HEIGHT: f32 = 100.0; // Магическое число.

WALL_HEIGHT — это высота в пикселях стены,
находящейся на расстоянии одной единицы от игрока.

Теперь давайте добавим в блок impl State функцию get_view:

impl State {
    /// Возвращает 160 высот стен с точки зрения игрока.
    pub fn get_view(&self) -> [i32; 160] {
        // FOV игрока разделена пополам по его углу обзора.
        // Чтобы получить первый угол луча, мы должны
        // прибавить половину FOV к углу игрока, вычислив
        // край FOV игрока.
        let starting_angle = self.player_angle + HALF_FOV;

        let mut walls = [0; 160];

        for (idx, wall) in walls.iter_mut().enumerate() {
            // "idx" - это номер луча, в котором мы находимся, "wall" - это
            // изменяемая ссылка на значение в "walls".
            let angle = starting_angle - idx as f32 * ANGLE_STEP;

            // Получаем ближайшие горизонтальное и вертикальное
            // пересечения со стенами для этого угла.
            let h_dist = self.horizontal_intersection(angle);
            let v_dist = self.vertical_intersection(angle);

            // Получаем минимальное из этих двух расстояния
            // и "преобразуем" его в высоту стены.
            *wall = (WALL_HEIGHT / f32::min(h_dist, v_dist)) as i32;
        }

        walls
    }
}

Выглядит неплохо, попробуем запустить! Игрока можно перемещать клавишами со стрелками на клавиатуре.
Отлично, нам удалось создать иллюзию глубины! Для первой попытки впечатляющий результат. Большинство туториалов на этом останавливаются, однако есть некоторые проблемы, которые нам нужно решить.

Исправление перспективы

При перемещении вы можете заметить, что всё выглядит… не совсем правильно. Стены изгибаются, как будто мы смотрим через объектив «рыбий глаз».

Это вызвано тем, что наш алгоритм ошибочно предполагает, что зрение человека сходится к одной бесконечно малой точке (игроку). В реальной жизни зрительная кора головного мозга постоянно смешивает точки зрения из обоих глаз, создавая глубину.

В данном случае гораздо более точной метафорой будет плоскость, перпендикулярная перспективе, испускающей лучи:

Разумеется, описание довольно расплывчатое, но оно станет понятнее, если воспринимать это как «коррекцию рыбьего глаза». Чтобы применить эту «коррекцию», нужно умножить расстояние на косинус разности между углом луча и углом игрока:

Где  — высота стены в пикселях,  — это расстояние до стены,  — разность между углом луча и углом игрока.

Чтобы применить эту корректировку, нам достаточно изменить единственную строку в функции State::get_view:

*wall = ( WALL_HEIGHT / (f32::min(h_dist, v_dist) * cosf(angle - self.player_angle)) ) as i32;

Отлично! Теперь стены прямые.

Добавление глубины

В текущей версии игры сложно различить разные стены. Особенно на расстоянии: стены сливаются друг с другом и сложно отличить их друг от друга.

В реальной жизни мы можем различать стены по их теням. Можно попробовать эмулировать это в игре, по разному раскрашивая стены в зависимости от их ориентации. К счастью, мы уже знаем, какие стены «смотрят на восток/запад», а какие «на север/юг» благодаря тому, какие лучи пересекаются с ними! Зная это, довольно легко назначить стенам разные цвета.

WASM-4 использует уникальный способ задания цвета, который функции применяют для отрисовки. При каждом вызове функции отрисовки в WASM-4 он решает, какой цвет использовать, на основании индекса, хранящегося в бите памяти, называемого DRAW_COLORS. В WASM-4 легко менять DRAW_COLORS, это делается при помощи простой шестнадцатеричной записи.

Давайте добавим DRAW_COLORS рядом с GAMEPAD1 в начале файла:

const DRAW_COLORS: *mut u16 = 0x14 as *mut u16;
const GAMEPAD1: *const u8 = 0x16 as *const u8;

Теперь мы можем переписать State::get_view так, чтобы она передавала, должна ли стена отрисовываться «с тенью» или нет:

impl State {
    /// Возвращает 160 высот стен и их "цвет" с точки зрения игрока.
    pub fn get_view(&self) -> [(i32, bool); 160] {
        // FOV игрока разделена пополам по его углу обзора.
        // Чтобы получить первый угол луча, мы должны
        // прибавить половину FOV к углу игрока, вычислив
        // край FOV игрока.
        let starting_angle = self.player_angle + HALF_FOV;

        let mut walls = [(0, false); 160];

        for (idx, wall) in walls.iter_mut().enumerate() {
            // "idx" - это номер луча, в котором мы находимся, "wall" - это
            // изменяемая ссылка на значение в "walls".
            let angle = starting_angle - idx as f32 * ANGLE_STEP;

            // Получаем ближайшие горизонтальное и вертикальное
            // пересечения со стенами для этого угла.
            let h_dist = self.horizontal_intersection(angle);
            let v_dist = self.vertical_intersection(angle);

            let (min_dist, shadow) = if h_dist < v_dist {
                (h_dist, false)
            } else {
                (v_dist, true)
            };

            // Получаем минимальное из этих двух расстояния
            // и "преобразуем" его в высоту стены.
            *wall = (
                (WALL_HEIGHT / (min_dist * cosf(angle - self.player_angle))) as i32,
                shadow,
            );
        }

        walls
    }
}

Теперь давайте внесём в fn update следующие изменения:

#[no_mangle]
unsafe fn update() {
    STATE.update(
        *GAMEPAD1 & BUTTON_UP != 0,
        *GAMEPAD1 & BUTTON_DOWN != 0,
        *GAMEPAD1 & BUTTON_LEFT != 0,
        *GAMEPAD1 & BUTTON_RIGHT != 0,
    );

    // обходим каждый столбец на экране и отрисовываем стены в центре.
    for (x, wall) in STATE.get_view().iter().enumerate() {
        let (height, shadow) = wall;

        if *shadow {
            // отрисовываем цветом 2 стены с "тенями"
            *DRAW_COLORS = 0x2;
        } else {
            // отрисовываем цветом 3 стены без "теней"
            *DRAW_COLORS = 0x3;
        }

        vline(x as i32, 80 - (height / 2), *height as u32);
    }
}

Давайте попробуем запустить:

Ого, выглядит намного лучше. Даже несмотря на то, что тени в реальном мире так себя не ведут, это добавляет хорошие детали и помогает создать иллюзию глубины.

Уменьшаем программу!

Если вы сейчас проверите размер программы, допустим, вызвав du -bh, то можете получить нечто подобное:

12K  target/wasm32-unknown-unknown/release/raycaster.wasm

Это гораздо больше, чем исполняемый файл в 2 КБ, который я обещал в заголовке, так как же нам его добиться? Один из способов уменьшения размера файлов .wasm — применение wasm-opt. Обычно получить wasm-opt можно, установив пакет binaryen. wasm-opt специально разработан для оптимизации файлов .wasm устранением мёртвого кода и дублирующихся команд, которые оставляет компилятор.

Давайте добавим в наш Makefile этап wasm-opt step in our Ma

© Habrahabr.ru