[Перевод] Модель взаимодействия судов с водой в видеоиграх: часть 206.09.2016 13:18

Добро пожаловать во вторую часть серии статей о физике судов в видеоиграх. В первой части я объяснял принципы выталкивания и обосновал выбор расчёта гидростатических сил, действующих на судно. Также я указал, что мы закладываем важный фундамент для расчёта не только гидростатических сил, но и для гидродинамических сил в нашей упрощённой модели. Я имею в виду, что мы рассчитаем дополнительные силы для каждого погружённого треугольника, суммируем их и приложим их к судну. Всё действительно будет настолько просто.

Или так может показаться на первый взгляд. Оказалось, что моделирование остальных сил для придания судну приемлемой динамической реакции потребовало гораздо больше исследований и итераций, чем закладка всего фундамента в части 1 и расчёт выталкивания. Ретроспективно первую часть можно сравнить с прогулкой в парке. Вторая часть больше похожа на бег по пересечённой местности в джунглях, полных ям-ловушек с кольями, когда за тобой гонятся голодные волки (т.е. продюсеры).

Если вы не читали первую часть, то вот краткий вывод. Судно моделируется как триангулированный меш. Мы аппроксимируем поверхность воды с полем высот и, используя быстрый алгоритм пересечения аппроксимированного треугольника с полем высот, определяем часть судна, находящуюся под водой как список погружённых треугольников. Каждый треугольник исходного меша может создавать 0, 1 или 2 полностью погружённых треугольника. Алгоритм в действии показан на Рисунке 1.

На Рисунке 2 представлено типичное распределение гидростатического давления на погружённую часть судна. В качестве грубой аппроксимации мы приняли, что давление постоянно на всей поверхности погружённого треугольника. Движение показанного здесь судна не является результатом только гидростатических сил.

Рисунок 2 — Распределение гидростатического давления, полученное в нашей модели. Следует учесть, что это поведение получено для полной модели, а не приложением к судну только гидростатических сил. Судно падает с высоты 2 метра и какое-то время замедляется. Затем оно телепортируется на 2 метра под воду, выталкивается на поверхность и также какое-то время замедляется. Давление считается постоянным для всего погружённого треугольника, и может быть довольно большим. Чем больше треугольники корпуса, тем грубее приближение. Однако модель работает и она стабильна даже при довольно низкополигональных мешах.

Как видно из Рисунка 3, приложение только гидростатических сил недостаточно для точной симуляции поведения тела в воде. По-моему, это отличная черта программирования и симуляции. Она даёт нам возможность проверить, достаточно ли близка заданная модель к реальному физическому поведению. В то время как мы безнадёжно медленно подходим к созданию хороших моделей для физических явлений, особенно в соответствии с точными математическими условиями, наши глаза и мозг способны быстро и с высокой точностью распознать симуляцию, непохожую на реальное поведение объектов. В нашем случае симуляция показывает нам, насколько важны для судна силы сопротивления, и что происходило бы, если бы они не существовали в какой-то очень странной упругой параллельной вселенной.

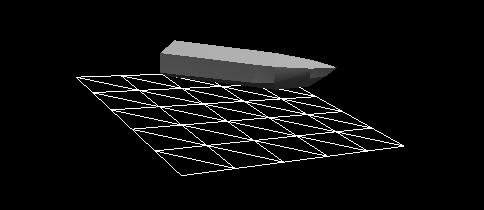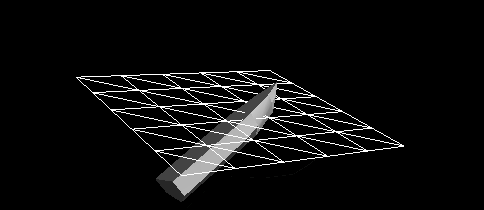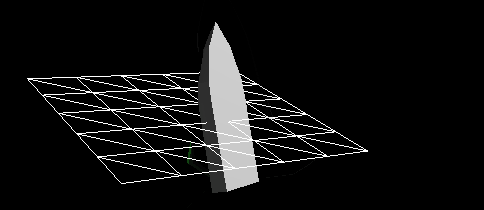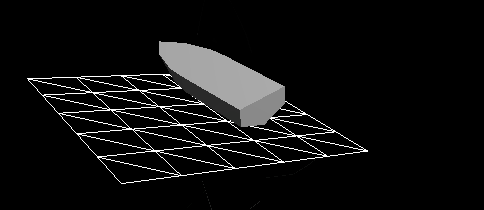
Рисунок 3 — Динамическая реакция судна, к которому приложены только гидростатические силы, на абсолютно плоской поверхности воды. Довольно сложно будет рыбачить с такой лодки. Очевидно, что силы сопротивления играют большую роль в реальном мире.

Похоже, что на Рисунке 3 лодка прикреплена к пружине, а не находится на воде. Из своего опыта мы знаем, что судно, сброшенное в воду с высоты, довольно быстро прекратит колебаться вверх-вниз. Это называется затуханием, замедление движения, вызванное противодействующими силами. В результате максимальная высота, достигаемая при движении вверх-вниз, становится всё меньше и меньше. В случае критического затухания силы достаточно велики, чтобы сразу прекратить колебания.

Забавы с патрульным катером из Just Cause 3. Симуляция воды выполняется NVIDIA WaveWorks.

Стабилизация модели

Когда я решил создать простую модель сил, действующих на судно, у меня был довольно туманный план того, чего я хочу достигнуть. Это было что-то между «разработкой стабильной модели лодки, которая реалистично реагирует на большие волны и которой интересно управлять» и «хм, насколько же это будет сложно?». Определив силы, которые нужно приложить к судну, мы должны стабилизировать их, чтобы оно не скакало бесконтрольно по воде. Кроме того, если мы введём слишком большие или нестабильные силы, нам нужна защита, чтобы судно не достигло безумных скоростей. Поэтому первое, что мы сделали, это добавили большие силы затухания и для линейных, и для угловых составляющих, чтобы стабилизировать колебания, о которых я говорил. Затухание просто пропорционально тому, насколько тело погружено в воду. Как вы можете помнить, каждый кадр мы определяем список погружённых треугольников, так что простейший расчёт погружённой части судна задаётся соотношением между погружённой площадью и общей площадью судна.

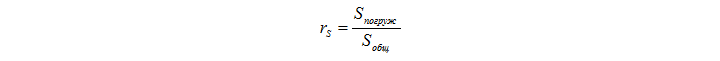
Например, мы можем ввести линейную силу затухания, выглядящую вот так:

или квадратичное затухание:

Перед погружением: спойлер

В конце мы используем 3 различные силы, возникающие вследствие взаимодействия судна и воды: вязкость воды, сопротивление давления и сила удара корпуса (или сила вхождения в воду). Каждая из этих сил была добавлена в модель, потому что каким-то образом соотносится с реальностью, а также потому что относится к определённой проблеме. В оставшейся части статьи я объясню, какие физические реалии эти силы должны представлять, а также расскажу, что мотивировало меня добавить эти силы, т.е. к какому спектру проблем относится каждая сила. Не забывайте, что это упрощённая модель, поэтому некоторые из сил довольно неявственно связаны с физической реальностью. В особенности это относится к сопротивлению давления, которое является огромным упрощением того, что связано с сопротивлением волн и брызговым сопротивлением в более сложной гидродинамической теории. Четвёртая сила, добавленная массовая сила, в окончательной модели не прижилась, но я всё ещё размышляю над тем, как учесть её в расчётах для лучшего ощущения инерции.

Уравнение сопротивления

Поскольку ниже мы много будем рассуждать о сопротивлении, я хочу остановиться на секунду и рассмотреть уравнение сопротивления. Если оно вам знакомо, вы можете перейти к следующему разделу. В динамике жидкости сопротивление
традиционно выражается в следующей форме:

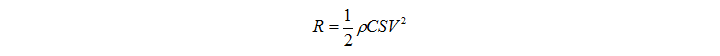
Составляющие треугольника

Прежде чем начать описание нашей модели гидродинамических сил, я введу величины и векторы, связанные с погружёнными треугольниками корпуса судна. Все силы рассчитываются с их помощью.

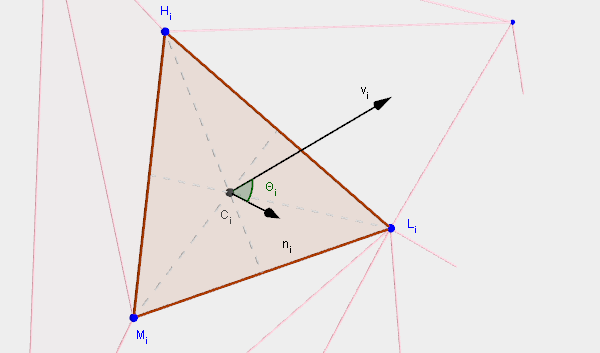
Рисунок 5 — Некоторые полезные величины для каждого погружённого треугольника.

Сопротивление вязкой жидкости

Я начну с сопротивления вязкой жидкости, как и начинаются многие тексты по гидродинамике. Сопротивление вязкости
возникает, когда вода течёт вдоль поверхности. Поскольку есть сильное взаимодействие между водой непосредственно рядом с корпусом и поверхностью корпуса, существует микроскопический слой воды, который практически «прилипает» к поверхности и движется вместе с судном. С увеличением расстояния от корпуса вода «прилипает» всё меньше и меньше. Чтобы немного упростить картину, каждый микроскопический слой воды на заданном расстоянии от поверхности взаимодействует с одним слоем прямо перед ним и с одним — непосредственно после него. Интенсивность такого взаимодействия называется вязкостью. Чем более жидкость вязкая, тем больше жидкости прилипает к поверхности и тянется за ней. (*) Это создаёт силу, называемую сопротивлением вязкой жидкости.

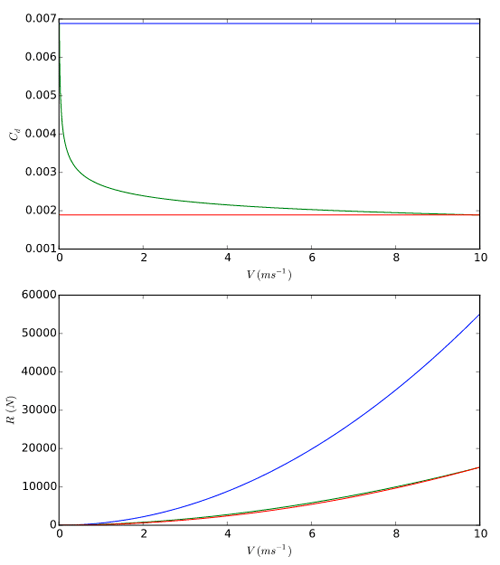
Проведено множество экспериментов по измерению сопротивления вязкой жидкости и существуют хорошие эмпирические формулы для прогнозирования создаваемого судном сопротивления вязкой жидкости. Для примера давайте возьмём гладкую плоскую пластину, перемещаемую под поверхностью воды. Если пластина тонкая и перемещается вдоль своей длины так, что не сталкивается с потоком, то измеряемая сила почти полностью возникает вследствие сопротивления вязкой жидкости. Во многих странах созданы специальные установки, называемые опытовые бассейны, для измерения, среди прочего, гидродинамических сил, действующих на перемещаемые в воде погружённые тела. Некоторые страны обсуждают полученные данные на Международной конференции опытовых бассейнов (ITTC), которая проводится каждые 3 года, начиная с 1933 года (только однажды был пропуск в 9 лет из-за Второй мировой войны). В 1957 году ITTC пришла к соглашению, что формула:

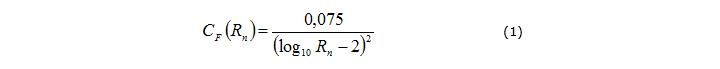
представляет собой очень хорошую аппроксимацию полученных данных. Эта формула называется формулой корреляции моделей судов и выведена не аналитически из основных принципов, а скорее является функцией регрессии, которая для практических целей достаточно близка к получаемым данным. Строго говоря, для нас это не очень важно, нам просто нужна какая-нибудь формула, которую мы можем применить к каждому из наших треугольников для расчёта вязкостного трения. Но это показывает нам, что физика динамики жидкости настолько сложна, что на практике ограничиваются измеряемым сопротивлением, а не применяют аналитические формулы.

Вязкость жидкости — это не единственный параметр, влияющий на величину силы. Во-первых, также важна шероховатость поверхности. Более шероховатая поверхность будет сильнее взаимодействовать с более толстым слоем воды, чем более гладкая. Ещё более важным является турбулентность потока рядом с поверхностью. Перед судном поток считается ламинарным. Он упорядочен и слои на увеличивающемся расстоянии от поверхности текут параллельно друг другу, пусть даже и с разными скоростями, поскольку они влияют на скорости друг друга на микроскопическом уровне вследствие вязкости (**). Но чем дольше жидкость течёт вдоль поверхности, тем более турбулентной она становится, и тем больше слоёв смешивается друг с другом. Когда различные слои турбулентно смешиваются, количество ускоренной поверхностью жидкости увеличивается, что приводит к повышению сопротивления. Так что нам следует ожидать большее сопротивление вязкой жидкости возле кормы судна по сравнению с носом. И, наконец, важна трёхмерная форма судна. Она отличается от плоской пластины и изменяет природу потока. Поскольку судно не совершенно плоское, жидкости нужно пройти большее расстояние и относительная скорость жидкости обычно выше, чем скорость судна. Из-за неплоской формы лодки давление вдоль поверхности изменяется, и это также влияет на сопротивление.

Когда судно перемещается по спокойной воде, сопротивление вязкой жидкости является единственной силой, действующей на судно. Возможно такое, что судно достаточно выдаётся из воды и движению противодействует относительно небольшая поверхность, но при этом большая часть днища касается воды. В этом случае сопротивление давления, которое мы рассмотрим ниже, будет довольно небольшим, однако нам всё равно потребуется высокое сопротивление воды. Кроме того, если мы сделаем судно в два или три раза длиннее без изменения фронтальной поверхности, нам нужно, чтобы сопротивление увеличилось, и мы добьёмся этого с помощью сопротивления вязкости, поскольку оно возникает в основном на треугольниках корпуса, расположенных по касательной к скорости.

Рисунок 6 — Динамическое поведение судна, подверженного кроме выталкивающей силы только сопротивлению вязкости. Несмотря на то, что используются очень хорошие эмпирические формулы сопротивления вязкой жидкости, которые довольно удобно применять, они совершенно не приводят к какому-либо затуханию движения судна. В этом случае судно сброшено с высоты один метр от поверхности воды. Сопротивление вязкой жидкости играет важную роль, но оно значительно только при высоких скоростях.

Силы сопротивления давления

Теперь мы переходим ко второй силе: силе сопротивления давления. Также здесь мы отойдём от серьёзной физики, и я объясню, почему.

В морской гидродинамике учёные разделяют сопротивление профиля волн, сопротивление разрушения волн, дополнительное сопротивление при ходе на волнении, брызговое сопротивление, вихреобразующие силы и т.д. Они не всегда соответствуют определённому физическому свойству. Скорее, это просто способы учёта в гидродинамике того факта, что общее сопротивление судну, движущемуся в воде. превышает сопротивление вязкости. Наблюдая за судном и окружающей его водой, можно понять, что энергия рассеивается не только вследствие сопротивления вязкости. Например, сопротивление профиля волн может быть оценено по наблюдениям за волнами, создаваемыми судном, и определением значения сопротивления, приложенного к судну сопротивления при помощи ньютоновского принципа действия и противодействия. Но большую часть времени создаваемые таким образом склоны волн должны быть небольшими. Это упрощает расчёт и позволяет создать довольно простую формулу. Однако это предположение неверно, поэтому сопротивление профиля волн составляет только часть сопротивления. Рядом с судном склоны волн не могут считаться незначительными, волны разрушаются, приводя к повышению сопротивления. Это называется сопротивлением разрушения волн. Затем, если выбрана соответствующая модель для расчёта сопротивления разрушения волн, может потребоваться выделить ещё одно сопротивление: брызговое сопротивление, оно возникает тогда, когда удар о воду настолько силён, что вода превращается в брызги. Конечно, всё это захватывающе интересно, но слишком сложно и не может применяться для нашей модели.

Вместо расчёта различных компонентов при помощи их разделения и оценки в качестве альтернативы мы можем численно решить уравнение Навье-Стокса. Однако, как я не устаю повторять, всё это лежит за пределами наших потребностей в отношении производительности и сложности модели.

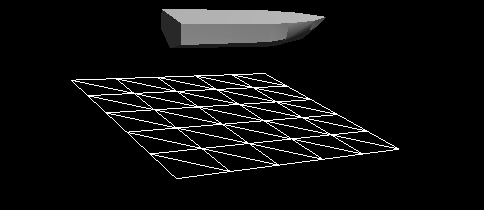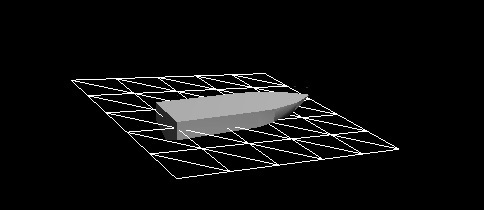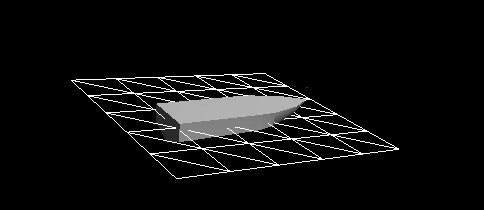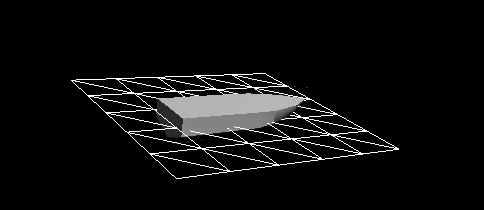
Рисунок 7 — Динамическая реакция с учётом сопротивления вязкости и сопротивления давления. Затухание теперь очень хорошо работает. Но оно всё ещё несовершенно. Динамическая реакция недостаточно жёсткая, сохраняются остаточные колебания. Можно увеличить затухание, выбрав большее значение для коэффициента сопротивления давления, но это приведёт к нереалистичной маневренности судна. Например, судно станет нереалистично быстро замедляться после движения с заданной скоростью, как будто судно идёт по грязи, а не по воде. Нам нужна ещё одна сила, отзывчивая к очень нелинейной или неквадратичной динамической реакции судна, взаимодействующего с водой.

Сила сопротивления давления действует по нормали к поверхности судна. На скорости она служит силой скольжения: если судно имеет достаточную движущую силу, чтобы преодолевать силу, противодействующую его ускорению, гидродинамическое давление повышается в нижней части судна, поднимая его вверх. При подъёме судна силами трения и давления создаётся меньшее сопротивление (за исключением днища судна). Именно поэтому глиссирующие суда обычно имеют более плоские днища, чтобы горизонтальная поверхность, на которую они опираются при скольжении, не уменьшалась при подъёме, только если они целиком не подняты из воды.

Силы удара корпуса

После приложения сопротивления вязкой жидкости и сопротивления давления поведение модели судна стало похожим на поведение судна. Однако судно по-прежнему может проникать в воду больше, чем допустимо, а общей реакции не достаёт жёсткости. Вместо изменения сил давления, которые мы хотели тщательно настроить для правильности поворотов и сил скольжения, мы решили ввести ещё одну силу, которая в основном будет отслеживать жёсткость реагирования жидкости на резкие ускорения или проникновения, которые почти похожи на столкновения жёстких тел.

Очень жёсткие столкновения будет сложно смоделировать с помощью силы, зависящей от глубины проникновения или смещения при использовании схемы дискретного интегрирования. Примером этого может быть очень жёсткая пружина. Поскольку сила пропорциональна смещению из положения покоя, то чем выше коэффициент жёсткости, тем сложнее симулировать пружину с фиксированным временным тактом. Существуют хорошо известные способы решения этой проблемы, но они делают интегрирование более сложным. Вместо выбора этого пути мы можем воспользоваться другой возможностью, потому что просто рассчитать силу, необходимую для полной остановки движения судна за один кадр. Поскольку важно, чтобы сила была произвольно жёсткой, а теория, связанная с силами удара корпуса очень сложна, мы решили упростить проблему и начать с абсолютно жёсткой реакции и необходимого возврата жёсткости в состояние равновесия. Мы начинаем с расчёта силы столкновения с водой. Если она очень велика, мы можем приложить силу, полностью останавливающее движение, при этом судно остановится, как будто столкнулось с землёй. С другой стороны, если столкновение имеет малую силу, мы можем предоставить полное управление движением другим силам и не прилагать силу, останавливающее движение. А между этими крайностями мы можем применять различные переходные функции (более или менее скачкообразные) для получения разных динамических результатов: линейные, степенные функции, сигмоидальные, ступенчатые.

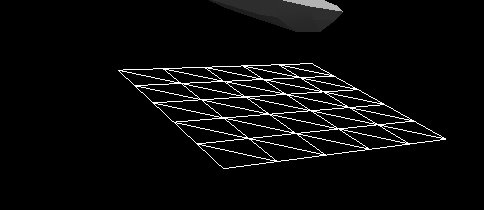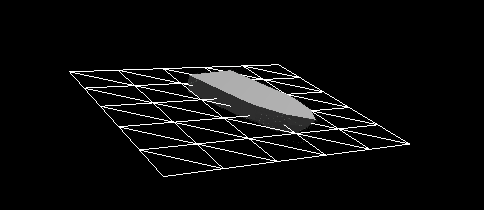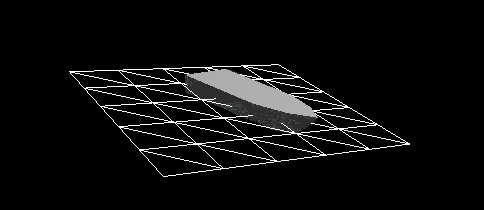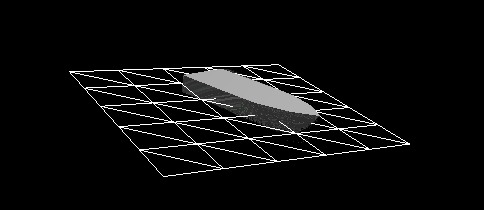
Рисунок 8 — Динамическая реакция с учётом сил удара корпуса судна, падающего в воду с высоты 2 м

Рисунок 9 — Судно на средних волнах, ускоренное до крейсерской скорости при движении по прямой. Приложенная здесь движущая сила очень проста, её источник расположен в задней части и немного толкает судно вверх. Жёсткость реакции становится сильнее с увеличением скорости. Возникает эффект подпрыгивания (дельфинирования), которого можно избежать сочетанием более тонкой настройки сил, оптимизации формы корпуса, регулировки движущей силы в зависимости от скорости, стабилизации аэродинамических сил. В правом нижнем углу показано распределение сил сопротивления давления по корпусу.

Заключение

Разработанная нами модель взаимодействия с водой применима для широкого диапазона размеров и форм судна, от двухметрового гидроцикла до 50-метрового корвета (см. Рисунок 10), а также для судов большего размера в условиях от штиля до шторма и без значительной настройки изменяемых переменных сил. Совершенно новый корпус с ранее не тестированными формой и размерами может быть брошен в воду с какой-нибудь движущей силой, и немедленно начнёт проявлять достаточно правильное поведение. Разумеется, приведение любого судна в транспортабельное состояние потребует правильного расположения и настройки двигателя (или двигателей), рулей, транцевых досок и другого стабилизирующего оборудования, но менее процедурный подход к гидростатике и гидродинамике корпуса занял бы гораздо больше времени на настройку с менее качественными результатами, которые к тому же не так хорошо справлялись со всеми возможными высотами и скоростями судна в воде.

Относительная простота модели подходит для наших нужд. Мы используем эйлеровское интегрирование вперёд, расчёты трёх сил отделены друг от друга, и они могут отдельно настраиваться; мы можем легко определить, если заданная сила воздействует слишком много или мало в заданном режиме. Если бы мы приняли большее допустимое время для расчётов (больше 1 мс), мы бы расширили текущую модель, а не выбрали бы более реалистичную и требующую большого объёма вычислений модель. Однако существуют возможности для усовершенствования в областях, которые мы рассмотрим ниже.

Одна из таких областей — сила, называемая силой присоединённой массы, или силой виртуальной массы; лучше всего её объясняет цитата из Википедии: «Смысл силы в том, что жидкость получает кинетическую энергию вследствие работы, выполняемой ускоряющимся погружённым телом. (…) Для судов присоединённая масса может легко достигать ¼ или ⅓ массы судна, и, таким образом, представляет собой значительную инерцию в дополнение к силам трения и силам волнового сопротивления.» Виртуальная масса не существует, пока скорость судна неизменна. При ускорении судна оно должно сместить и ускорить определённую пропорциональную часть жидкости перед собой. При замедлении определённая пропорциональная часть жидкости вокруг судна, получившая кинетическую энергию, стремится передать эту энергию обратно судну в направлении, обратном замедлению. Было бы нежелательно действительно изменять массу судна для реализации этого эффекта. Работа с судном, чья масса изменяется, может быть очень запутанной; поэтому гораздо предпочтительнее обращаться с силой виртуальной массы так же, как и с любой другой силой, чтобы можно было сравнивать их и оценивать её влияние на способность маневрирования судном, как и для всех остальных сил. Мы предприняли попытки реализации этой силы, но не добились того, на что надеялись; возможно, так получилось из-за недостатка времени.

Ещё одна область, в которой возможны улучшения — сравнение сил в имеющейся модели с силами, действующими на корпус, согласно реалистичной вычислительной симуляции гидродинамики (computational fluid dynamics, CFD). Существуют open source-пакеты для расчёта CFD, такие как OpenFOAM [6], которые уже содержат готовые примеры для симулирования поведения корпуса судна в воде. В качестве такого примера можно привести бенчмарк корпуса Wigley (Wigley hull benchmark). Он содержит корпус, форма которого полностью математически определена и может использоваться для настройки различных коэффициентов. Это позволяет с лёгкостью сравнивать различные симуляции друг с другом или с данными towing tank, поскольку корпуса могут изготавливаться с высокой степенью точности. Такой подход требует возможности запуска CFD для корпуса в подробно описанных интересующих конфигурациях и извлечения информации о силах для сравнения. Также он требует многих часов расчётов на мощных машинах для получения нескольких секунд данных. Однако это может стать стоящим вкладом для исправления тех областей, в которых силы упрощённой модели наиболее отличаются от результатов расчётов CFD.

Также в 1964 году Дэниэлом Савицки были разработаны эмпирические формулы для призматических глиссирующих корпусов (т.е. для корпусов, имеющих чётко определённую и простую форму). Эти формулы определяют «силу плавучести, сопротивление, область смачивания, центр давления (…) как функцию скорости, угла атаки, угла подъёма и нагрузки.» Эти формулы можно использовать для регулировки сил в нашей модели с помощью тестирования на похожем корпусе в симуляции. [5]

Рисунок 10 — Большое разнообразие судов, которые можно симулировать в нашей модели. Первое судно в этом видео — корвет длиной около 50 м. Второе судно — тяжёлый патрульный катер, форма корпуса которого совершенно отличается. Последнее судно имеет несколько очень плоских корпусов малого размера (что-то вроде катамарана). Мы успешно симулировали даже такие маленькие суда, как гидроциклы. Симуляция воды выполняется NVIDIA WaveWorks. [9]

Послесловие

Помните, что когда мы начали вычислять гидродинамические силы, сначала мы добавили сильное искусственное затухание для стабилизации системы. С таким сильным затуханием выталкивающая сила отлично работала, например, для плавающей бочки. Поэтому я несколько преждевременно обрадовался. Когда мы перешли к формам судов, достичь того, что нам хотелось, удалось не так просто. Хуже того, мы с командой даже не могли прийти к консенсусу относительно того, почему то, что мы видим, выглядит неестественно. Такое случается, когда цели определены недостаточно чётко. Теперь я осознаю, что мы могли бы быстрее перейти к финальной модели, более подробно исследовав поведение судна в воде. Например, определив частоты и амплитуды движения судна в состоянии покоя с небольшим возмущением; ответив на следующие вопросы: сколько времени нужно судну, чтобы достичь максимальной скорости с нулевой? сколько нужно судну времени, чтобы «затормозить» со, скажем, крейсерской скорости до нуля? как долго оно делает полный поворот? насколько велик дифферент судна (как высоко поднимается его нос) на скорости? каков обычный угол скольжения судна при повороте? насколько судно теряет скорость при повороте, если он начат при максимальной скорости? Все эти вопросы в сущности очень сложны, поскольку существует множество форм и размеров судов, с которыми мы хотим иметь дело. Масса обычного транспорта варьируется в пределах множителя 1000, от мотоцикла (~100 кг) до огромного грузовика (100 тонн), масса же судов может изменяться от того же нижнего предела (100 кг) до 90 000 тонн авианосца, то есть со множителем 900 000. Также существует множество форм судов, что значительно влияет на их поведение.

Задав себе эти вопросы и ответив на них, даже приблизительно, мы стали двигаться гораздо быстрее. Например, из [1] и [2] я выяснил, что обычно дифферент глиссирующих судов составляет примерно 4 градуса, угол скольжения при резком повороте — около 20, а угол при повороте — 25 градусов или больше. Эти значения были очень полезны, потому что по какой-то причине мы пытались избежать слишком большого угла скольжения, что заставило нас занизить некоторые константы и спутало нам все карты в самом начале.

Было захватывающе наблюдать, как при добавлении реалистичных сил к модели мы начали сталкиваться с теми же инженерными проблемами, что и у разработчиков судов в реальном мире. Я получил следующий комментарий к первой части этой серии статей от читателя по имени Грэг Шил (Greg Sheel): «Есть такая мысль: если вы реализуете достаточно реалистичную модель судна на воде, ваше судно в игре с определённой степенью точности должно иметь точно такую же конструкцию, что и настоящее судно; в противном случае его поведение на воде будет ужасным». Он был абсолютно прав, и это привело меня к интересной дилемме в симуляции физики транспортных средств. Чем более реалистична симуляция, тем больше она будет сталкиваться с реалистичными проблемами. Замечательно, когда симуляция начинает вести себя как в реальности, игроки действительно ценят и чувствуют это, однако только если это не мешает самой игре. Признак того, что мы находились на правильном пути — форма корпуса сильно влияет на стабильность судна в состоянии покоя. В частности, угол подъёма или форма кормы меняют всё. Но больший реализм означает, что нам потребуется много времени от времени разработки на устранение проблем, возникших вследствие более реалистичного подхода. В случае модели судна мы заметили серьёзные проблемы со стабильностью в некоторых режимах. Позже мы узнали, что эти проблемы возникают в реальности и известны как «дельфинирование», cork-screwing, chine walking (примечание переводчика: не нашёл русскоязычных эквивалентов этим терминам) и т.д.

Благодарности

Я хочу поблагодарить своих коллег из Avalanche Studios: Хэмиша Янга (Hamish Young) за важные инсайты и отзывы, бесконечный оптимизм и энтузиазм при разработке модели, а также за его несравненные навыки в настройке судов, сделавшей их интересными в управлении; Рональда Лестерлина (Roland Lesterlin) на то, что видел потенциал в нашем подходе и веру в возможность реализации модели вовремя; Криса Гловера (Chris Glover) за воплощение судов с помощью программирования спецэффектов, таких как волны Кельвина, которые сами по себе заслуживают отдельной статьи, а также заполнения водой; the чрезвычайно талантливого Омара Шакира (Omar Shakir), спродюсировавшего самые захватывающие моменты игры (всё ещё не могу поверить, что они настолько хорошо выглядят); всех остальных членов команды Just Cause 3 за создание такой интересной и качественной игры. Я благодарю моего отца Ричарда за правку черновиков обеих частей этой серии статей и за то, что освежил мои знания по физическим темам, которые он уже объяснял мне 25 лет назад. И, наконец, я с нежностью говорю «спасибо» моей жене Зои за её терпение и поддержку, а также за то, что позволяла мне читать книги по физике практически на рождественском столе.

Примечания

(*) Различные жидкости имеют разную вязкость. Например, йогурт очень вязкий. Похоже, что шведы этого не замечают, потому что они продолжают продавать йогурт в картонных упаковках для молока. Я узнал это, посетив впервые Avalanche Studios в Стокгольме. В конце концов, половина содержимого прилипает к стенкам упаковки, когда пытаешься вылить его. Приходится выдавливать йогурт из упаковки как зубную пасту. И вы уже думаете, что избегать при первом посещении магазина покупок еды в тюбиках было хорошей идеей!

(**) Удивительный факт о ламинарном потоке заключается в том, что он обратим (на макроскопическом уровне). Для иллюстрации этого можно привести популярный эксперимент, заключающийся в заливании прозрачного глюкозного сиропа в цилиндрический резервуар, внешняя стенка которого может вращаться вокруг его оси. Резервуар также имеет внутреннюю цилиндрическую стенку, которая остаётся неподвижной. Влив три капли кукурузного сиропа разных цветов в различные точки резервуара, мы начинаем медленно вращать внешнюю стенку для создания ламинарного потока; три цветных точки начинают «размазываются» в круг относительно оси вращения и выглядят так, как будто смешиваются. Но если начать вращать внешнюю стенку в противоположном направлении, можно вернуться к почти тому же исходному состоянию с тремя точками, находящимися точно там, где они были в начале. Обратимость ламинарного потока, продемонстрированная в Университете Нью-Мексико.

Ссылки

Hydrodynamics of High-Speed Marine Vehicles. Odd M. Faltinsen
Stability of a planing craft in turning motion. Y. Ikeda, H. Okumura and T. Katamaya
International Towing Tank Conference
Drag Equation
Principles of Yacht Design. Lars Larsson, Rolf E. Eliasson and Michal Orych
OpenFOAM
Hydrodynamic Design of Planing Hulls. Marine Technology, D. Savitsky
Procedures for Hydrodynamic Evaluation of Planing Hulls in Smooth and Rough Water. D. Savitsky, P.W. Brown
NVIDIA WaveWorks