[Перевод] Математика, помирившая Ньютона с квантовым миром

Как профессор математики перестал бояться и полюбил алгебраическую геометрию.
На шестом десятке уже поздно становиться настоящим специалистом по алгебраической геометрии, но мне наконец-то удалось в неё влюбиться. Как и следует из её названия, этот раздел математики использует для изучения геометрии алгебру. Примерно в 1637 году Рене Декарт заложил фундамент этой области знаний, взяв плоскость, мысленно нарисовав на ней сетку и обозначив координаты за x и y. Можно записать уравнение вида x2+ y2 = 1, и получить кривую, состоящую из точек, координаты которых удовлетворяют этому уравнению. В этом примере мы получим круг.
Для того времени это была революционная идея, потому что она позволяет нам системным образом преобразовывать вопросы геометрии в вопросы об уравнениях, которые при достаточном знании алгебры можно решить. Некоторые математики занимались этой великолепной областью всю свою жизнь. Мне она до последнего времени не нравилась, но я смог связать её с моим интересом к квантовой физике.
В детстве физика нравилась мне больше математики. Мой дядя Альберт Баэз, отец знаменитой фолк-певицы Джоан Баэз, работал на ЮНЕСКО и помогал развивающимся странам с обучением физике. Мои родители жили в Вашингтоне. Когда дядя приезжал в город, он открывал свой портфель, доставал оттуда магниты или голограммы, и с их помощью объяснял мне физику. Это было потрясающе. Когда мне было восемь лет, он подарил мне написанный им учебник по физике для колледжа. Хотя я и не мог его понять, но сразу понял, что хочу этого. Я решил стать физиком, и родители обеспокоились, потому что знали, что для физики нужна математика, а я в ней был не очень силён. Деление в столбик казалось мне невыносимо скучным, и я отказывался делать домашнюю работу по математике с её бесконечно повторяющейся рутиной. Но позже, когда я осознал, что играясь с уравнениями, смогу больше узнать о Вселенной, она меня увлекла. Загадочные символы походили на волшебные заклинания, и в каком-то смысле так оно и было. Наука — это магия, которая на самом деле работает.
В колледже я выбрал основным предметом математику, и заинтересовался вопросом физика-теоретика Юджина Вигнера о «необъяснимой эффективности» математики: почему наша Вселенная с такой готовностью подчиняется математическим законам? Он формулировал это так: «Чудо адекватности языка математики для формулировки законов физики есть восхитительный дар, который мы не постигаем и не заслуживаем». Будучи юным оптимистом, я чувствовал, что эти законы дадут нам подсказки для решения более глубокой головоломки: почему Вселенная вообще управляется математическими законами. Я уже понимал, что математика слишком объёмна, чтобы изучить её целиком, поэтому в магистратуре решил сосредоточиться на том, что было важно мне. И одним из тех, что мне не казалось важным, была алгебраическая геометрия.
Как математик может не влюбиться в алгебраическую геометрию? Причина в следующем: в своём классическом виде эта область исследует только полиномиальные уравнения — уравнения, которые описывают не просто кривые, но и фигуры более высокой размерности, называемые «многообразиями». То есть x2+ y2= 1 — это нормально, как и x43– 2xy2= y7. Но уравнение с синусами, косинусами или другими функциями находится за пределами этой области, если только мы не найдём какого-то способа преобразовать его в уравнение из многочленов. Студенту магистратуры это казалось ужасным ограничением. В конце концов, в задачах физики используется множество функций, не являющихся многочленами.
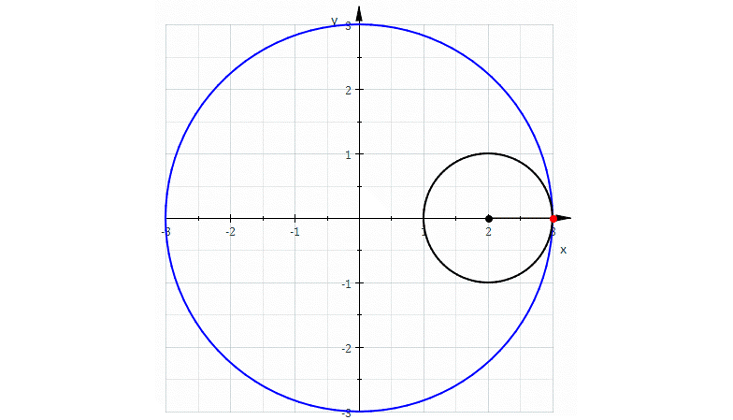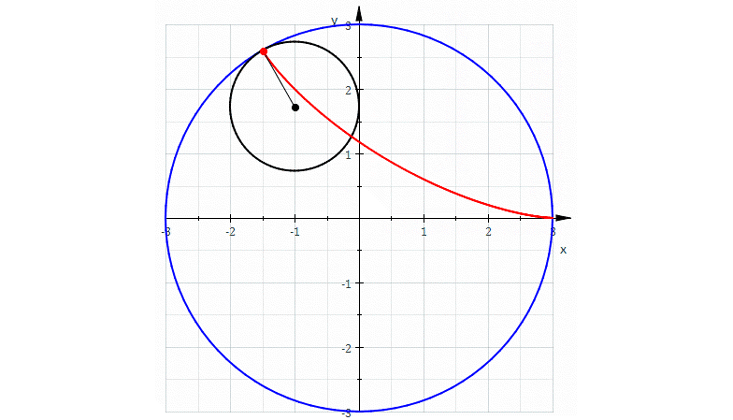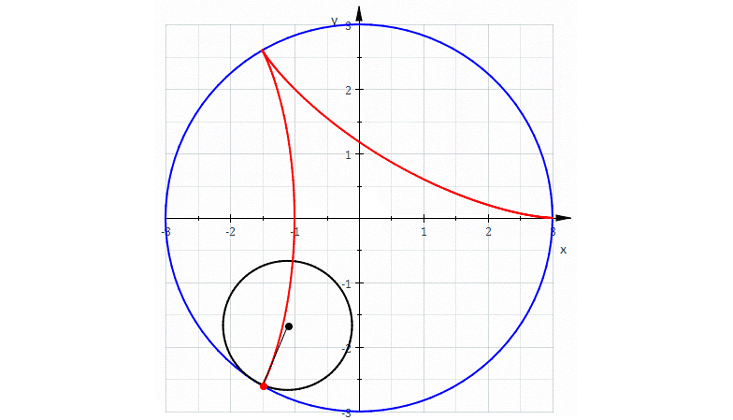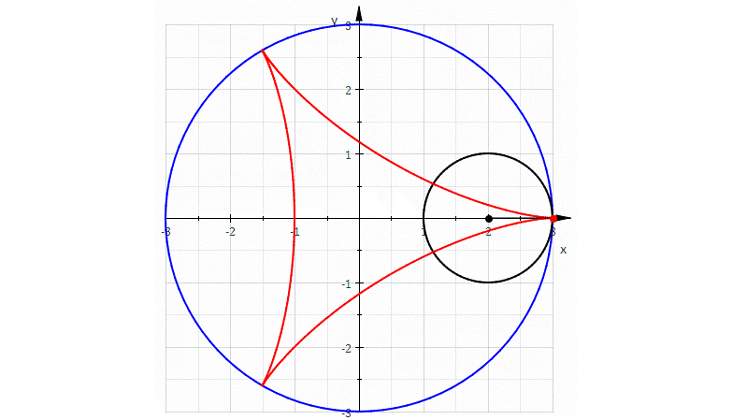
Для этого есть многочлен: с помощью одних многочленов можно описать множество интересных кривых. Например, прокатим окружность внутри другой окружности размером в три раза больше. Получим кривую с тремя острыми углами, которая называется «дельтоидой». Неочевидно, что можно описать её полиномиальным уравнением, но это так. Великий математик Леонард Эйлер придумал его в 1745 году.
Почему алгебраическая геометрия ограничивает себя многочленами? Математики изучают всевозможные виды функций, но хотя они и очень важны, на каком-то уровне их сложность только отвлекает от фундаментальных загадок связи между геометрией и алгеброй. Ограничив ширину своих поисков, алгебраическая геометрия может глубже исследовать эти загадки. Она занималась этим веками, и теперь мастерство работы с многочленами поистине поражает: алгебраическая геометрия превратилась в мощный инструмент теории чисел, криптографии и многих других областей. Но для её истинных почитателей ценность этой области заключается в самой себе.
Однажды я встретил студента магистратуры из Гарварда и спросил его, что он изучает. Напыщенным тоном он сказал одно слово: «Хартсхорн». Он имел в виду учебник Робина Хартсхорна «Алгебраическая геометрия», опубликованный в 1977 году. Предполагается, что он должен стать введением в предмет, но на самом деле очень сложен. Процитируем описание из Википедии: «Первая глава под названием «Многообразия» рассказывает о классической алгебраической геометрии многообразий над алгебраически замкнутыми полями. В этой главе используется множество классических результатов из коммутативной алгебры, в том числе теорема Гильберта о нулях, и часто встречаются отсылки книгам Атьи-Макдональда, Мацумуры и Зарисского-Самуэля».
Если вы ничего не поняли… то это я и имел в виду. Чтобы разобраться даже в первой главе Хартсхорна, нужен довольно большой объём фоновых знаний. Читать Хартсхорна — это как пытаться догнать гениев многих веков, стремившихся бежать со всех ног.

Знаменитая кубическая: это кубическая узловая поверхность Кэли. Она знаменита тем, что это многообразие с наибольшим количеством узлов (таких острых штук), которые можно описать кубическим уравнением. Уравнение имеет вид (xy + yz + zx)(1 — x — y — z) xyz = 0 и называется «кубическим» потому, что одновременно мы перемножаем не более трёх переменных.
Одним из этих гениев был научный руководитель Хартсхорна — Александр Гротендик. Примерно с 1960 по 1970 годы Гротендик совершил революционный переворот в алгебраической геометрии, сделав её частью эпичного путешествия с целью доказательства гипотез Вейля, связывающих многообразия с решениями проблем из теории чисел. Гротендик предположил, что гипотезы Вейля можно подтвердить, усилив и углубив связь между геометрией и алгеброй. У него было чёткое представление о том, как это должно произойти. Но для обеспечения точности этой идеи требовался огромный труд. Чтобы выполнить его, он организовал семинар. Гротендик почти каждый день выступал с докладами и воспользовался помощью лучших математиков Парижа.

Давай пробежим матема-фон: Александр Гротендик на своём семинаре.
Безостановочно работая в течение десятилетия, они написали тысячи страниц новой математики, наполненной ошеломительными концепциями. В конце концов, воспользовавшись этими идеями, Гротендик успешно доказал все гипотезы Вейля, кроме последней, самой сложной. К удивлению Гротендика, её решил его студент.
В течение его наиболее продуктивных лет, даже несмотря на доминирование во французской школе алгебраической геометрии, многие математики считали идеи Гротендика «слишком абстрактными». Это звучит немного странно, учитывая то, насколько абстрактна вся математика. Но несомненно то, что для восприятия его идей требуются время и усилия. Будучи студентом магистратуры, я старался от них отдалиться, потому что активно сражался с изучением физики: в ней гении тоже веками творили на полной скорости, и чтобы добраться до передового рубежа, приходится долго догонять. Но позже, когда я начал свою карьеру, мои исследования привели меня к работе Гротендика.
Если бы я выбрал другой путь, то мог подойти к его работе через изучение теории струн. Физики, изучающие теорию струн, постулируют, что кроме видимых измерений пространства и времени (трёх измерений для пространства и одного для времени) существуют дополнительные измерения пространства, настолько скрученные, что их невозможно увидеть. В некоторых их теориях эти дополнительные измерения образуют многообразие. Поэтому, исследователи теории струн легко могут столкнуться со сложными вопросами из алгебраической геометрии. А это, в свою очередь, заставляет их столкнуться с Гротендиком.

Я совсем запутался: срез одного многообразия, называемого «трёхмерным многообразием пятого порядка» (quintic threefold), которое можно использовать для описания дополнительных свёрнутых измерений пространства в теории струн.
И в самом деле. лучше всего теорию струн рекламирует не успешное предсказание экспериментальных результатов — этим она совершенно не может похвастаться —, а способность решать проблемы в пределах чистой математики, в том числе и алгебраической геометрии. Например, теория струн потрясающе хорошо может подсчитывать количество кривых разного вида, которые можно отрисовать в определённых многообразиях. Поэтому сегодня можно увидеть теоретиков струн, общающихся с алгебраическими геометрами, и каждая из сторон при этом может удивить другую своими открытиями.
Но источник моего личного интереса к работе Гротендика был другим. У меня всегда были серьёзные сомнения в теории струн, а подсчёт кривых в многообразиях — это последнее, чем бы я хотел заниматься: это как скалолазание — очень увлекательно наблюдать, но слишком страшно, чтобы заниматься самому. Оказалось, что идеи Гротендика насколько обобщены и сильны, что распространяются за пределы алгебраической геометрии на множество других областей. В частности, на меня произвела большое впечатление его 600-страничная неопубликованная рукопись Pursuing Stacks, написанная в 1983 году. В ней он заявляет, что топология (если объяснять в широком смысле, то это теория о том, какие формы может принимать пространство, если нас не волнует его изгибание или растягивание, а интересуют только виды отверстий) может быть целиком сведена к алгебре!
Поначалу эта идея может показаться аналогичной алгебраической геометрии, в которой мы используем алгебру для описания геометрических фигур (например, кривых или многообразий более высокой размерности). Но оказывается, что «алгебраическая топология» имеет совершенно другой привкус, потому что в топологии мы не обязаны ограничиваться фигурами, описываемыми полиномиальными уравнениями. Вместо работы с прекрасными драгоценностями, мы имеем дело с гибкими, мягкими сгустками; поэтому нам нужна другая алгебра.

Если нужно объяснение: математики иногда шутят, что топологи не видят разницы между пончиком и чашкой кофе.
Алгебраическая топология — это красивая область, существовавшая задолго до Гротендика, но он был одним из первых, кто серьёзно предложил метод сведения всей топологии к алгебре. Благодаря моей работе в физике его предложение показалось мне чрезвычайно восхитительным. И вот почему: в тот момент я взялся за сложную задачу объединения двух лучших теорий физики: квантовой физики, описывающей все силы, кроме гравитации, и общей теории относительности, описывающей гравитацию. Похоже, что пока мы этого не сделаем, наше понимание фундаментальных законов физики обречено быть неполным. Но реализовать это чертовски трудно. Причина заключается в том, что квантовая физика основана на алгебре, а в общей теории относительности активно используется топология. Но это подсказывает нам направление атаки: если мы сможем выяснить, как свести топологию к алгебре, то это, возможно, поможет нам сформулировать теорию квантовой гравитации.
Мои коллеги-физики на этом моменте взвыли бы и начали жаловаться, что я слишком всё упрощаю: в квантовой физике используется не просто алгебра, а общая теория относительности — это не только топология. Тем не менее, именно возможные физические преимущества сведения топологии к алгебре восхитили меня в работе Гротендика.
Поэтому начиная с 1990-х я пытался разобраться в мощных абстрактных концепциях, изобретённых Гротендиком, и на сегодняшний день добился частичного успеха. Некоторые математики считают эти концепции сложной частью алгебраической геометрии. Но теперь они кажутся мне простой частью. Для меня сложной частью стали не все эти абстрактные концепции, а их скучные подробности. Во-первых, это весь тот материал в текстах, которые Хартсхорн считает обязательными предпосылками: «книги Атья-Макдональда, Мацумуры и Зарисского-Самуэля», а это огромные объёмы алгебры. Но есть ещё и многое другое.
Поэтому хотя у меня теперь и есть часть того, что необходимо для чтения Хартсхорна, до недавнего времени изучение этих материалов слишком страшило меня. Студент-физик однажды спросил знаменитого специалиста о том, сколько математики должен знать физик. Специалист ответил: «Больше, чем он знает». И в самом деле, изучение математики никогда нельзя считать законченным, поэтому я сосредоточился на аспектах, которые казались самыми важными и/или интересными. До прошлого года алгебраическая геометрия никогда не оказывалась в начале этого списка.
Что же изменилось? Я осознал, что алгебраическая геометрия связана с отношениями между классической и квантовой физикой. Классическая физика — это физика Ньютона, в которой мы предполагаем, что можем измерить всё с полной точностью, хотя бы в теории. Квантовая физика — это физика Шрёдингера и Гейзенберга, ею управляет принцип неопределённости: если мы измеряем некоторые аспекты физической системы с полной точностью, другие должны оставаться неопределёнными.
Например, любой вращающийся объект обладает «угловым моментом». В классической механике мы визуализируем его стрелкой, направленной вдоль оси вращения, и длина этой стрелки пропорциональна скорости вращения объекта. А в классической механике мы предполагаем, что можем точно измерить эту стрелку. В квантовой механике — более точном описании реальности — это оказывается неверным. Например, если мы знаем, насколько далеко указывает стрелка в направлении x, то не можем узнать. насколько далеко она указывает в направлении y. Эта неопределённость слишком мала, чтобы заметить её для баскетбольного мяча, но для электрона она очень существенна: пока физики не начали это учитывать, у них было только грубое понимание электронов.
Физики часто стремятся «квантифицировать» задачи классической физики. То есть они начинают с классического описания какой-то физической системы и пытаются вывести квантовое описание. Для выполнения этой работы не существует какой-то общей и полностью систематизированной процедуры. И это не должно вас удивлять: эти два взгляда на мир сильно отличаются. Однако существуют полезные рецепты для выполнения квантизации. Наиболее систематизированные из них применимы к очень ограниченному множеству физических задач.
Например, в классической физике мы иногда можем описать систему точкой в многообразии. Не стоит ожидать, что это возможно в общем случае, но во многих важных случаях такое происходит. Например, рассмотрим вращающийся объект: если мы зафиксируем длину стрелки его углового момента, то стрелка всё равно может указывать в любом направлении, то есть её конец должен лежать на сфере. Таким образом, мы можем описать вращающийся объект точкой на сфере. И эта сфера на самом деле является многообразием, «сферой Римана», названной в честь одного из величайших алгебраических геометров 19-го века Бернхарда Римана.

Многообразие: поверхность Эндрасса восьмого порядка — это красивый высокосимметричный пример «многообразия»: фигуры, описываемой полиномиальными уравнениями. Алгебраическая геометрия начиналась как исследование подобных фигур.
Когда задача классической физики описывается многообразием, происходит магия. Процесс квантизации становится совершенно систематичным и на удивление простым. Существует даже своего рода обратный процесс, который можно назвать «классизацией» — он позволяет преобразовать квантовое описание обратно в классическое описание. Классический и квантовый подходы к физике становятся тесно связанными, мы можем брать идеи из любого подхода и наблюдать за тем, что они могут сказать нам о другом. Например, каждая точка в многообразии описывает не только состояние классической системы — в нашем примере это конкретное направление углового момента —, но и состояние соответствующей квантовой системы, даже несмотря на то, что последняя управляется принципом неопределённости Гейзенберга. Квантовое состояние — это «наилучшее квантовое приближение» к классическому состоянию. Более того — в этой ситуации многие базовые теоремы из алгебраической геометрии могут рассматриваться как факты о квантизации. Так как я долгое время занимался квантизацией, это меня чрезвычайно радует.
Ричард Фейнман однажды сказал, что для продвижения в решении сложной физической задачи ему нужно взглянуть на неё под особым углом:
»[…] Мне нужно думать, что у меня есть какой-то кратчайший путь решения текущей проблемы. То есть как будто у меня есть талант, которым не пользуются другие, или особый взгляд, который они по глупости не посчитали превосходным взглядом на вещи. Мне необходимо думать, что по какой-то причине мои шансы выше, чем у других. В глубине души я знаю, что скорее всего эта причина ложна, и вероятнее всего, выбранный мной взгляд уже использовался другими. Но меня это не волнует: я обманываю себя, убеждая, что у меня есть дополнительный шанс».
Возможно, именно этого мне до недавнего времени не хватало в алгебраической геометрии. Разумеется, алгебраическая геометрия — это не просто задача, которую нужно решить, а комплекс знаний —, но это настолько огромная, пугающая совокупность, что я не решался касаться его, пока не нашёл этот кратчайший путь. Теперь я могу читать Хартсхорна, переводить некоторые из результатов в факты о физике, и у меня появился шанс на понимание всего этого. Это превосходное ощущение.
Об авторе: Джон Баэз — профессор математики из Калифорнийского университета в Риверсайде и приглашённый исследователь Центра квантовых технологий Сингапура. Он ведёт блог Azimuth о математике, естественных науках и проблемах окружающих среды. Подписывайтесь на него в Twitter: @johncarlosbaez.
