[Перевод] Как пересчитать электронную таблицу

Поток данных в этой таблице немного сложно проследить, поэтому вот эквивалентная диаграмма, которая представляет таблицу в виде графа:

Округляем стоимость буррито El Farolito super vegi до 8 долларов, поэтому при доставке стоимостью 2 доллара общая сумма составит 20 долларов.
О, совсем забыл! Одному из моих друзей мало одного буррито, ему нужно два. Поэтому я в реальности хочу заказать три. Если обновить Num Burritos, наивный механизм электронных таблиц может пересчитать весь документ, пересчитав сначала ячейки без входных данных, а затем пересчитав каждую ячейку с готовыми входными данными, пока ячейки не закончатся. В этом случае мы сначала рассчитаем цену буррито и количество, затем цену буррито с доставкой, а затем новую итоговую сумму в размере 30 долларов.

Эта простая стратегия пересчета всего документа может показаться расточительной, но на самом деле она уже лучше, чем было в VisiCalc, первых электронных таблицах в истории, и первом так называемом убойному приложению, благодаря которому стали популярными компьютеры Apple II. VisiCalc многократно пересчитывал ячейки слева направо и сверху вниз, сканируя их снова и снова, хотя ни одна из них не менялась. Несмотря на такой «интересный» алгоритм, VisiCalc оставался доминирующим программным обеспечением для электронных таблиц в течение четырёх лет. Его правление закончилось в 1983 году, когда Lotus 1–2–3 захватил рынок «пересчётом в естественном порядке» (natural-order recalculation). Вот как его описывал Трейси Робнетт Ликлайдер в журнале Byte:
Lotus 1–2–3 использовал пересчёт в естественном порядке, хотя также поддерживал построчный и поколончатый режимы VisiCalc. Пересчёт в естественном порядке поддерживал список зависимостей ячеек и пересчитывал ячейки с учётом зависимостей.
Lotus 1–2–3 реализовал стратегию «пересчитывать всё», показанную выше. В течение первого десятилетия развития электронных таблиц это был самый оптимальный подход. Да, мы пересчитываем каждую ячейку в документе, но только один раз.
Но что насчёт цены буррито с доставкой
Действительно. В моём примере с тремя буррито нет причин пересчитывать цену одного буррито с доставкой, потому что изменение количества буррито в заказе не может повлиять на цену буррито. В 1989 году один из конкурентов Lotus понял это и создал SuperCalc5, предположительно назвав его в честь теории супер буррито, лежащей в основе этого алгоритма. SuperCalc5 пересчитывал «только ячейки, зависящие от изменённых ячеек», так что обновление количества буррито становилось примерно таким:
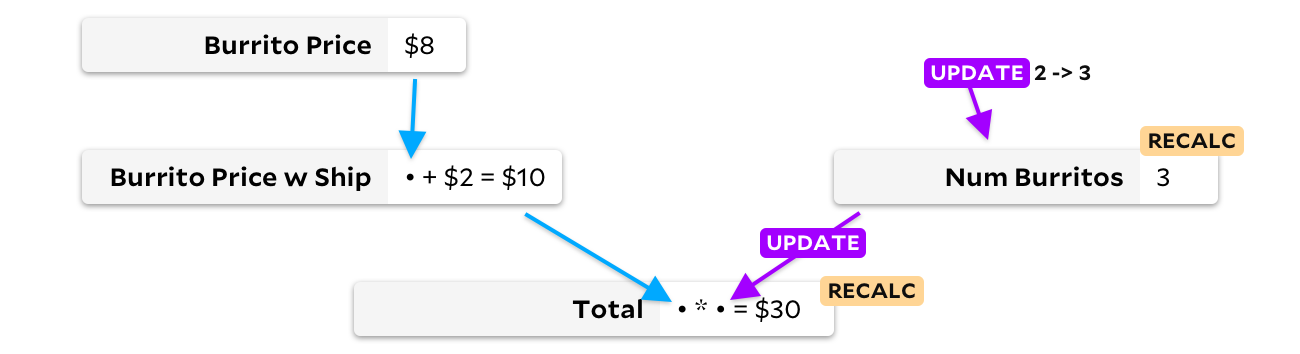
Обновляя ячейку только при изменении входных данных, мы можем избежать пересчёта цены буррито с доставкой. В этом случае мы сэкономим всего одно сложение, но в больших электронных таблицах экономия может оказаться гораздо более существенной! К сожалению, сейчас у нас другая проблема. Скажем, мои друзья теперь хотят мясные буррито, которые на доллар дороже, а закусочная El Farolito добавляет 2 доллара к заказу независимо количества буррито. Прежде чем что-то пересчитать, посмотрим на граф:
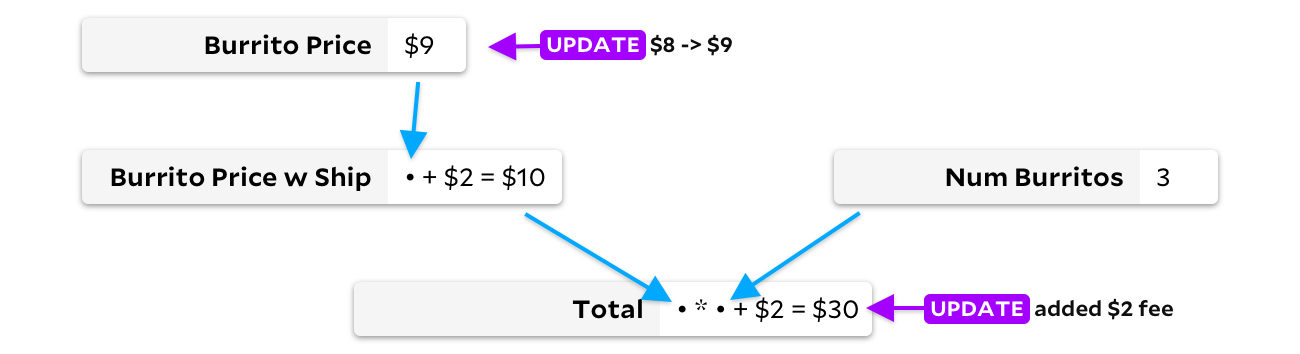
Поскольку здесь обновляются две ячейки, у нас проблема. Следует сначала пересчитать цену одного буррито или общую? В идеале мы сначала вычисляем цену буррито, замечаем изменение, затем пересчитываем цену буррито с доставкой и, наконец, пересчитываем Total. Однако, если мы вместо этого сначала пересчитаем общую сумму, нам придётся пересчитать ее во второй раз, как только новая цена буррито 9 долларов распространится вниз по ячейкам. Если мы не вычисляем ячейки в правильном порядке, этот алгоритм не лучше, чем пересчёт всего документа. В некоторых случаях такой же медленный, как VisiCalc!
Очевидно, нам важно определить правильный порядок обновления ячеек. В общем, есть два решения этой проблемы: загрязнение ячеек (dirty marking) и топологическая сортировка.
Первое решение включает в себя маркировку всех ячеек вниз по потоку от обновлённой ячейки. Они помечаются как грязные. Например, когда мы обновляем цену буррито, то помечаем нижестоящие ячейки Burrito Price w Ship и Total, прежде чем делать какой-либо пересчёт:
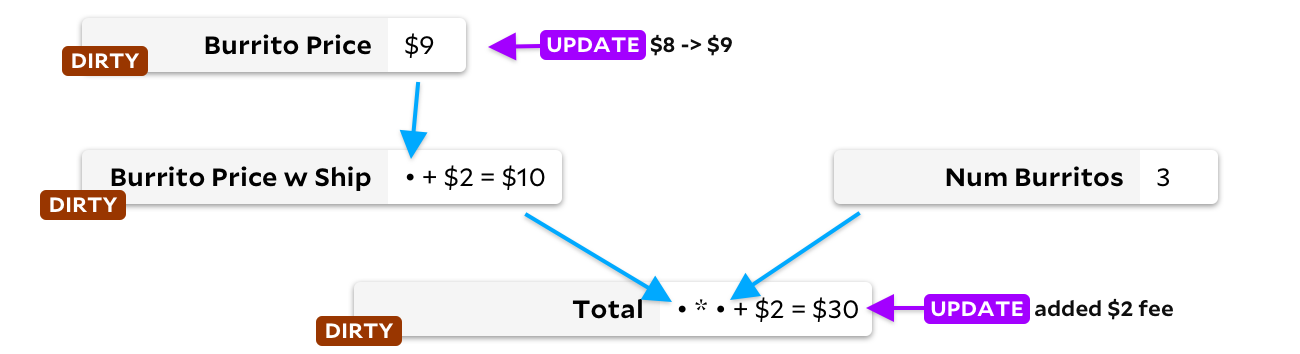
Затем в цикле находим грязную ячейку без грязных входов — и пересчитываем её. Когда грязных ячеек не останется, мы закончили! Это решает нашу проблему с зависимостями. Однако есть один недостаток — если ячейка пересчитана и мы обнаружили, что новый результат совпадает с предыдущим, мы всё равно пересчитаем нижестоящие ячейки! Немного дополнительной логики поможет избежать проблемы, но, к сожалению, мы всё равно тратим время на маркировку ячеек и снятие маркировки.
Второе решение — топологическая сортировка. Если у ячейки нет входных данных, мы помечаем её высоту как 0. Если есть, отмечаем высоту как максимум высоты входящих ячеек плюс один. Это гарантирует, что у каждой ячейки значение высоты больше, чем у любой из входящих ячеек, поэтому мы просто отслеживаем все ячейки с изменённым входом, всегда выбирая для пересчёта в первую очередь ячейку с самой низкой высотой:
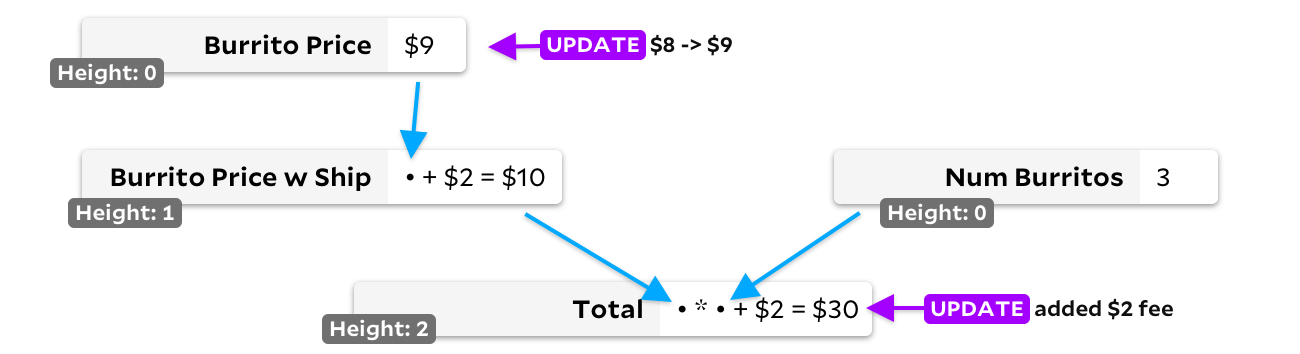
В нашем примере с двойным обновлением цена буррито и общая сумма изначально будут добавлены в кучу пересчёта. Цена буррито имеет меньшую высоту и будет пересчитана в первую очередь. Поскольку её результат изменился, мы затем добавим в кучу пересчёта цену буррито с доставкой, и поскольку у неё тоже высота меньше, чем у Total, то она будет пересчитана до того, как мы окончательно пересчитаем Total.
Это намного лучше первого решения: ни одна ячейка не маркируется грязной, если одна из входящих ячеек действительно не изменится. Однако это требует сохранять ячейки в отсортированном порядке в ожидании пересчёта. При использовании кучи это приводит к замедлению O(n log n), что в худшем случае асимптотически медленнее, чем стратегия Lotus 1–2–3 по пересчёту всего.
Современный Excel применяет сочетание загрязнения и топологической сортировки, подробнее см. в их документации.
Ленивые вычисления
Теперь мы более или менее достигли алгоритмов пересчёта в современных электронных таблицах. Подозреваю, что в принципе нет никаких бизнес-обоснований для дальнейших их улучшений, к сожалению. Люди уже написали достаточно формул Excel, чтобы миграция на любую другую платформу стала невозможной. К счастью, я не разбираюсь в бизнесе, поэтому мы всё равно рассмотрим дальнейшие улучшения.
Кроме кэширования, один из интересных аспектов вычислительного графа в стиле электронных таблиц заключается в том, что мы можем вычислять только те ячейки, которые нас интересуют. Это иногда называют ленивыми вычислениями или demand-driven computation. В качестве более конкретного примера приведём немного расширенный график электронной таблицы с буррито. Пример такой же, как и раньше, но мы добавили то, что лучше всего описать как «расчёт сальсы». Каждый буррито содержит 40 граммов сальсы, и мы выполняем быстрое умножение, чтобы узнать, сколько сальсы во всём заказе. Поскольку в нашем заказе три буррито, всего будет 120 граммов сальсы.

Конечно, проницательные читатели уже заметили проблему: общий вес сальсы в заказе — довольно бесполезная метрика. Кого волнует, что это 120 грамм? Что мне делать с этой информацией? К сожалению, обычная электронная таблица потратит циклы на расчёт сальсы, даже если большую часть времени нам эти расчёты не нужны.
Именно здесь может помочь ленивый перерасчёт. Если каким-то образом указать, что нас интересует только результат Total, можно было бы пересчитать эту ячейку, её зависимости и не трогать сальсу. Давайте назовём Total наблюдаемой ячейкой, поскольку мы пытаемся посмотреть на её результат. Мы также можем назвать Total и три её зависимости необходимыми ячейками, поскольку они необходимы для вычисления некоторой наблюдаемой ячейки. Salsa In Order и Salsa Per Burrito назовём ненужными (unnecessary).
Для решения этой проблемы некоторые товарищи из команды Rust создали фреймворк Salsa, явно назвав его в честь ненужных вычислений сальсы, на которые тратились циклы их компьютеров. Наверняка они могут лучше меня объяснить, как он работает. Очень грубо, фреймворк использует номера ревизий для отслеживания того, нуждается ли ячейка в пересчёте. Любая мутация в формуле или входных данных увеличивает глобальный номер ревизии, и каждая ячейка отслеживает две ревизии: verified_at для ревизии, результат которой был обновлён, и changed_at для ревизии, результат которой был фактически изменён.
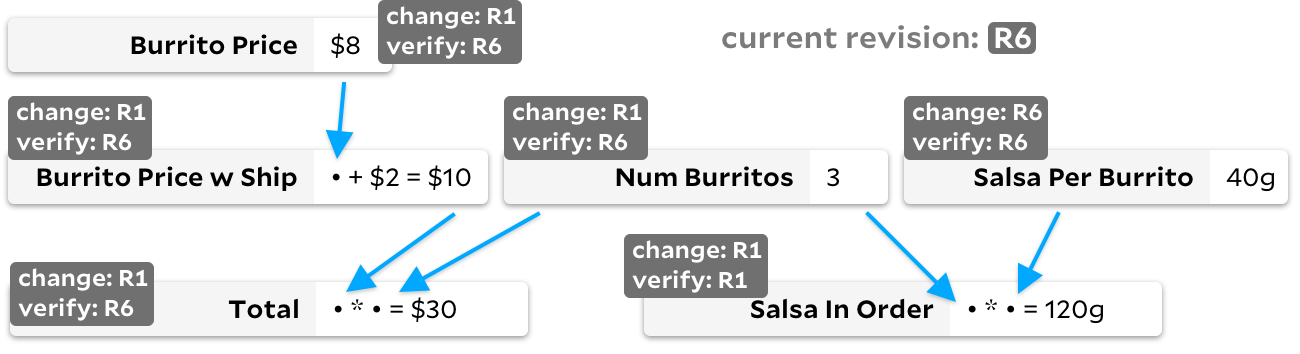
Когда пользователь указывает, что ему нужно новое значение Total, мы сначала рекурсивно пересчитываем все ячейки, необходимые для Total, пропуская ячейки, в которых ревизия last_updated равна глобальной ревизии. Как только зависимости Total обновлены, мы повторно запускаем фактическую формулу Total только в том случае, если либо у Burrito Price w Ship, либо у Num Burrito ревизия changed_at больше, чем проверенная ревизия Total. Это отлично подходит для Salsa в rust-analyzer, где важна простота, а вычисление каждой ячейки требует значительного времени. Однако в графике с буррито выше можно заметить и недостатки — если Salsa Per Burrito постоянно меняется, то наш глобальный номер ревизии будет часто повышаться. В результате каждое наблюдение Total потребует прохода трёх ячеек, даже если ни одна из них не изменилась. Никакие формулы не будут пересчитаны, но если график большой, многократное прохождение всех зависимостей ячейки может оказаться дорогостоящим.
Более быстрые варианты ленивых вычислений
Вместо того, чтобы изобретать новые ленивые алгоритмы, попробуем воспользоваться двумя классическими алгоритмами электронных таблиц, упомянутыми ранее: маркировкой и топологической сортировкой. Как можно представить, ленивая модель усложняет обе эти задачи, но обе по-прежнему жизнеспособны.
Сначала посмотрим на маркировку. Как и раньше, когда мы меняем формулу ячейки, то помечаем все нижестоящие ячейки как грязные. Поэтому при обновлении Salsa Per Burrito это будет выглядеть примерно так:

Но вместо того, чтобы немедленно пересчитать все грязные ячейки, мы ждём, пока пользователь не пронаблюдает ячейку. Затем запускаем на ней алгоритм Salsa, но вместо того, чтобы перепроверять зависимости с устаревшими номерами версий verified_at, мы перепроверяем только ячейки, помеченные как грязные. Такую технику использует Adapton. В такой ситуации наблюдение ячейки Total обнаруживает, что она не грязная, и поэтому мы можем пропустить проход по графу, который бы выполнила Salsa!
Если же пронаблюдать Salsa In Order, то она помечена как грязная, и поэтому мы перепроверим и пересчитаем и Salsa Per Burrito, и Salsa In Order. Даже здесь есть преимущества по сравнению с использованием только номеров ревизий, поскольку мы сможем пропустить рекурсивный проход по всё ещё чистой ячейке Num Burritos.
Ленивая грязная маркировка работает фантастически при частом изменении набора ячеек, которые мы пытаемся наблюдать. К сожалению, у неё те же недостатки, что и у предыдущего алгоритма грязной маркировки. Если изменяется ячейка со многими нижестоящими ячейками, то мы тратим много времени на маркировку ячеек и снятие маркировки, даже если входные данные фактически не изменяются, когда мы перейдём к пересчёту. В худшем случае каждое изменение приводит к тому, что мы помечаем весь граф как грязный, что даёт нам примерно тот же порядок производительности, что и алгоритм Salsa.
Кроме грязной маркировки, мы можем адаптировать для ленивых вычислений и топологическую сортировку. Это метод использует библиотека Incremental от Джейн Стрит, и для правильной работы требуется ряд серьёзных трюков. Прежде чем реализовать ленивые вычисления, наш алгоритм топологической сортировки использовал кучу, чтобы определить, какая ячейка будет пересчитана следующей. Но сейчас мы хотим пересчитывать только те ячейки, которые необходимы. Как? Мы не хотим ходить по всему дереву из наблюдаемых ячеек, как Adapton, поскольку полный проход по дереву разрушает всю цель топологической сортировки и даст нам характеристики производительности, аналогичные Adapton.
Вместо этого Incremental поддерживает набор ячеек, которые пользователь отметил наблюдаемыми, а также набор ячеек, необходимых для любой наблюдаемой ячейки. Всякий раз, когда ячейка помечена как наблюдаемая или ненаблюдаемая, Incremental ходит по зависимостям этой ячейки, чтобы убедиться, что необходимые метки применены правильно. Затем мы добавляем ячейки в кучу пересчёта только в том случае, если они помечены как необходимые. В нашем графе буррито, если только Total является частью наблюдаемого множества, изменение Salsa in Order не приведёт ни к какому проходу по графу, так как пересчитываются только необходимые ячейки:

Это решает нашу проблему без нетерпеливого хождения по графику, чтобы пометить ячейки как грязные! Мы всё ещё должны помнить, что ячейка Salsa per Burrito является грязной, чтобы пересчитать её позже, если это станет необходимым. Но в отличие от алгоритма Adapton, нам не нужно проталкивать эту единственную грязную метку вниз по всему графу.
Anchors, гибридное решение
И Adapton, и Incremental проходят граф, даже если не пересчитывают ячейки. Incremental ходит по графу вверх, когда изменяется набор наблюдаемых ячеек, а Adapton ходит по графу вниз, когда изменяется формула. С маленькими графами может быть не сразу очевидной высокая цена этих проходов. Но если граф большой и ячейки относительно дёшево вычисляются — часто так происходит с электронными таблицами — вы обнаружите, что большая часть вычислений уходит на ненужное хождение по графу! Когда ячейки дёшевы, маркировка бита на ячейке может стоить примерно столько же, сколько просто пересчёт ячейки с нуля. Поэтому в идеале, если мы хотим, чтобы наш алгоритм был существенно быстрее, чем простое вычисление, следует избегать ненужного хождения по графу, насколько это возможно.
Чем больше я думал об этой проблеме, тем больше понимал, что они тратят время на проход графа в примерно противоположных ситуациях. В нашем графе буррито давайте представим, что формулы ячеек редко меняются, но мы быстро переключаемся, сначала наблюдая Total, а затем Salsa in Order.
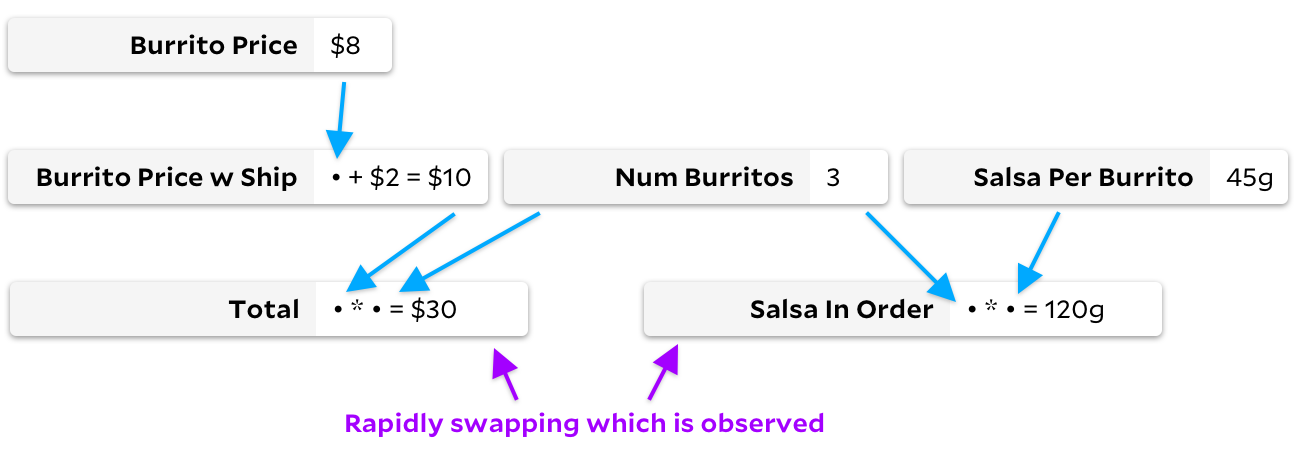
В этом случае Adapton не пойдёт по дереву. Никакие входные данные не меняются, и поэтому нам не нужно помечать никакие ячейки. Поскольку ничто не помечено, каждое наблюдение дёшево, поскольку мы можем просто немедленно вернуть кэшированное значение из чистой ячейки. Однако Incremental плохо работает в этом примере. Хотя никакие значения не пересчитываются, Incremental будет многократно отмечать и отменять отметку многих ячеек как необходимые или ненужные.
В противоположном случае давайте представим граф, где наши формулы быстро меняются, но мы не меняем список наблюдаемых ячеек. Например, мы могли бы представить, что наблюдаем Total, быстро меняя цену буррито с 4+4 на 2*4.
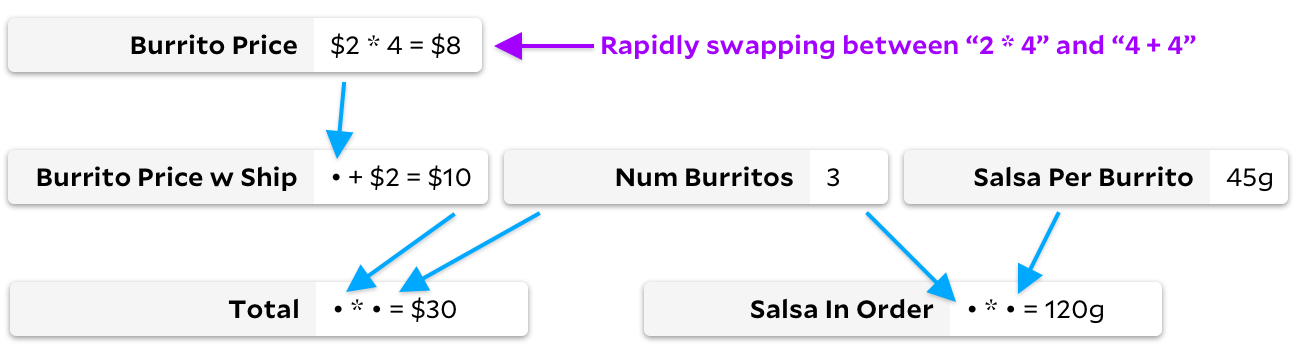
Как и в предыдущем примере, мы на самом деле не пересчитываем много ячеек: 4+4 и 2*4 равно 8, поэтому в идеале мы пересчитываем только это арифметическое действие, когда пользователь делает это изменение. Но в отличие от предыдущего примера, Incremental теперь избегает хождения по дереву. С помощью Incremental мы кэшировали тот факт, что цена буррито является необходимой ячейкой, и поэтому, когда она меняется, мы можем пересчитать её, не проходя по графу. С помощью Adapton мы тратим время на маркировку Burrito Price w Ship и Total как грязной, даже если результат Burrito Price не изменяется.
Учитывая, что каждый алгоритм хорошо работает в вырожденных случаях другого, почему бы в идеале просто не обнаруживать эти вырожденные случаи и не переключаться на более быстрый алгоритм? Это то, что я попытался реализовать в моей собственной библиотеке Anchors. Она запускает оба алгоритма одновременно на одном и том же графе! Если это звучит дико, ненужно и слишком сложно, то вероятно потому, что так оно и есть.
Во многих случаях Anchors точно следуют алгоритму Incremental, что позволяет избежать вырожденного случая Adapton выше. Но когда ячейки помечены как ненаблюдаемые, их поведение немного расходится. Давайте посмотрим, что происходит. Начнём с пометки Total как наблюдаемой ячейки:
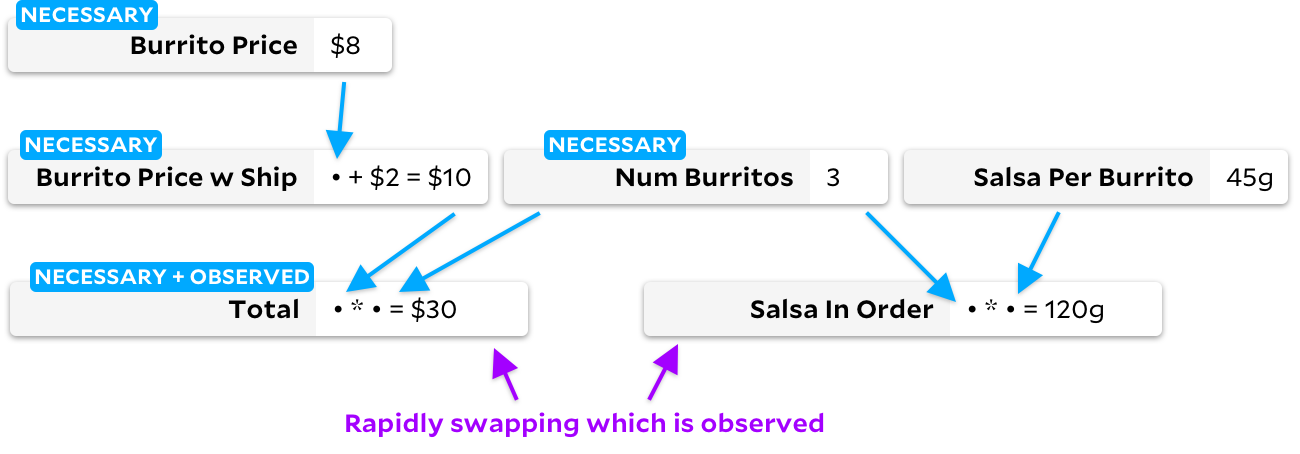
Если затем пометить Total как ненаблюдаемую ячейку, а Salsa in Order как наблюдаемую, традиционный алгоритм Incremental изменит граф, пройдя в процессе через все ячейки:
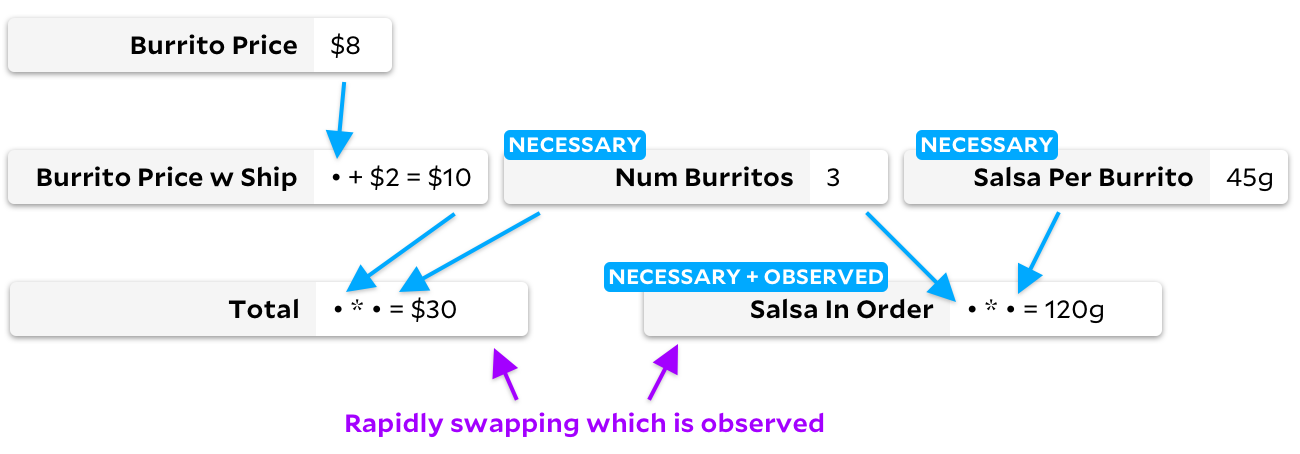
Anchors для этого изменения тоже обходит все ячейки, но создаёт другой граф:
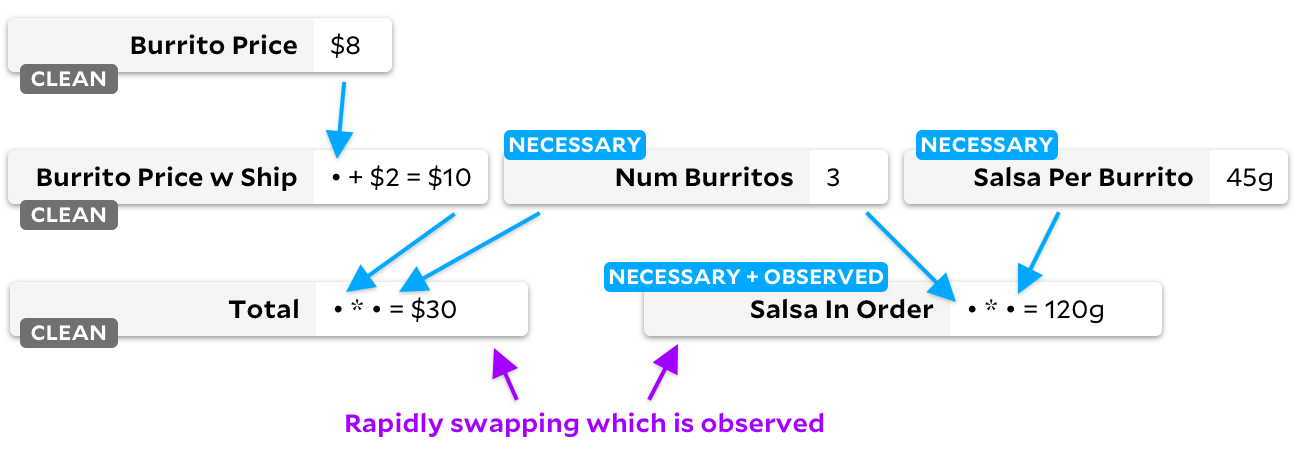
Обратите внимание на флаги «чистых» ячеек! Когда ячейка больше не нужна, мы помечаем ее как чистую. Давайте посмотрим, что происходит, когда мы переходим от наблюдения Salsa in Order к Total:
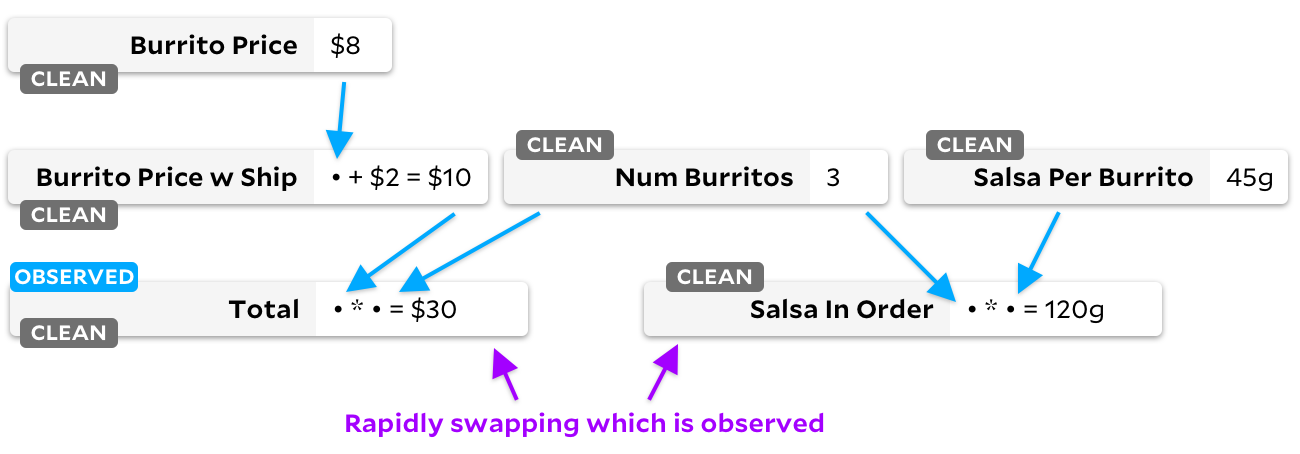
Правильно — на нашем графике теперь нет «необходимых» ячеек. Если у ячейки «чистый» флаг, мы никогда не помечаем её как наблюдаемую. С этого момента, независимо от того, какую ячейку мы помечаем как наблюдаемую или ненаблюдаемую, Anchors никогда не будет тратить время на ходьбу по графу — она знает, что ни один из входных сигналов не изменился.
Похоже, в закусочной El Farolito объявили скидку! Давайте снизим цену буррито на доллар. Как Anchors узнает, что нужно пересчитать сумму? До какого-либо пересчёта давайте посмотрим, как Anchors видит граф сразу после изменения цены буррито:

Если у ячейки чистый флаг, мы запускаем на ней традиционный алгоритм Adapton, охотно помечая нижестоящие ячейки как грязные. Когда мы позже запустим алгоритм Incremental, мы можем быстро сказать, что есть наблюдаемая ячейка, помеченная как грязная, и знаем, что нужно пересчитать её зависимости. Окончательный граф будет выглядеть следующим образом:
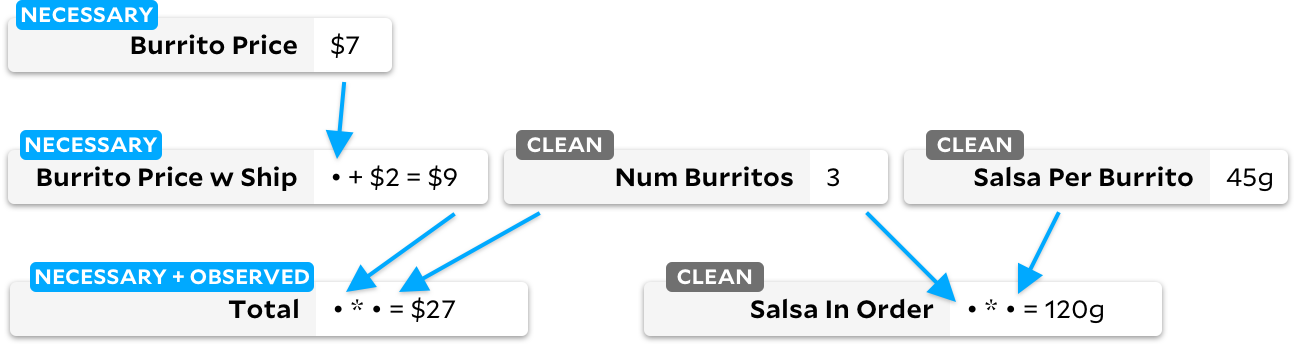
Мы пересчитываем ячейки только в случае необходимости, поэтому всякий раз, когда мы пересчитываем грязную ячейку, мы также помечаем её как необходимую. На высоком уровне вы можете представить эти три состояния ячеек как циклическую машину состояний:

На необходимых ячейках запускаем алгоритм топологической сортировки Incremental. На остальных запускаем алгоритм Adapton.
Синтаксис буррито
В заключение хотел бы ответить на последний вопрос: до сих пор мы обсуждали множество проблем, которые вызывает ленивая модель для нашей стратегии пересчёта таблицы. Но проблемы не только в алгоритме: есть и синтаксические проблемы. Например, давайте составим таблицу, чтобы выбрать эмодзи буррито для нашего клиента. Мы бы хотели написать инструкцию
IF в такой таблице: 
Поскольку традиционные электронные таблицы не являются ленивыми, мы можем вычислять B1, B2 и B3 в любом порядке, а потом вычислить ячейку IF. Однако в ленивом мире, если мы сначала можем вычислить значение B1, то можем посмотреть результат, чтобы узнать, какое значение нужно пересчитать — B2 или B3. К сожалению, в традиционных электронных таблицах IF не может выразить это!
Проблема: B2 одновременно ссылается на ячейку B2 и извлекает её значение. Большинство упомянутых в статье ленивых библиотек вместо этого явно различают ссылку на ячейку и акт извлечения её фактического значения. В Anchors мы называем эту ссылку на ячейку якорем (anchor). Подобно тому, как в реальной жизни буррито обёртывает кучу ингредиентов вместе, тип Anchor обёртывает T. Таким образом, я полагаю, наша ячейка с веганским буррито становится Anchor, своего рода нелепым буррито из буррито. Функции могут передавать наши Anchor столько, сколько им захочется. Но когда они на самом деле разворачивают буррито, чтобы получить доступ к Burrito внутри, мы создаём в нашем графе ребро зависимости, указывая алгоритму перерасчёта, что ячейка может быть необходима и нуждается в пересчёте.
Подход, принятый Salsa и Adapton, состоит в том, чтобы использовать вызовы функций и нормальный поток управления как способ развернуть эти значения. Например, в Adapton мы могли бы записать ячейку «Буррито для клиента» примерно так:
let burrito_for_customer = cell!({
if get!(is_vegetarian) {
get!(vegi_burrito)
} else {
get!(meat_burrito)
}
});Различая ссылку на ячейку (здесь
vegi_burrito) и акт развёртывания её значения (get!), Adapton может работать поверх операторов потока управления Rust, таких как if. Это отличное решение! Однако нужно немного магического глобального состояния для правильного подключения вызовов get! к ячейкам cell!, когда меняется is_vegetarian. Библиотека Anchors под влиянием Incremental использует менее магический подход. Подобно pre-async / await Future, Anchors позволяет запускать на Anchor такие операции, как map и then. Так, приведённый выше пример будет выглядеть примерно так: let burrito_for_customer: Anchor = is_vegetarian.then(|is_vegetarian: bool| -> Anchor {
if is_vegetarian {
vegi_burrito
} else {
meat_burrito
}
}); Дальнейшее чтение
В этой и без того длинной и витиеватой статье не хватило места для очень многих тем. Надеюсь, эти ресурсы смогут пролить немного больше света на эту очень интересную проблему.
- Семь реализаций Incremental, отличный углубленный взгляд на внутренние компоненты Incremental, а также куча оптимизаций, таких как постоянное увеличение высоты, о которых у меня не было времени говорить, плюс умные способы обработки ячеек, изменяющих зависимости. Также стоит почитать у Рона Мински: Разбор FRP.
- Видео с объяснениями, как работает Salsa.
- Это тикет Salsa, где Мэтью Хаммер, создатель Adapton, терпеливо объясняет отсечки какому-то случайному прохожему (мне), который никак не поймёт, как они работают.
- В выступлении Рафа Левиена на Rustlab есть несколько действительно интересных вещей на эту тему в контексте графических интерфейсов. Для этой статьи он сказал, что «Как работает автотрекинг» и «Автотрекинг: элегантный DX через ультрасовременный CS» — это отличные ресурсы.
- Должен признать, что на самом деле не понимаю «Дифференциальный поток данных», но это основа базы данных Materialize. Планирование запросов в целом кажется возможным решением больших проблем с отсутствием кэша, от которых страдают многие из этих фреймворков. В ней нет встроенных ленивых вычислений, но Джейми Брэндон (спасибо!) любезно указал мне на сообщение в их блоге «Латеральные соединения и ленивые запросы», которое объясняет, как добавить ленивые вычисления в качестве входных данных. Также стоит упоминания проект Noira от Массачусетского технологического института.
- Документация Adapton очень обширна.
- Оказывается, этот способ мышления применим и к системам сборки. Это одна из первых научных статей о сходствах между системами сборки и электронными таблицами.
- Slightly Incremental Ray Tracing — слегка инкрементный трассировщик лучей, написанный на Ocaml.
- Только что посмотрел «Частичное состояние в материализованных представлениях на основе потока данных», и оно кажется актуальным.
- Skip и Imp тоже выглядят очень интересно.
И конечно, вы всегда можете посмотреть мой фреймворк Anchors.
