[Перевод] Как новая нейронная сеть Facebook решает дифференциальные уравнения
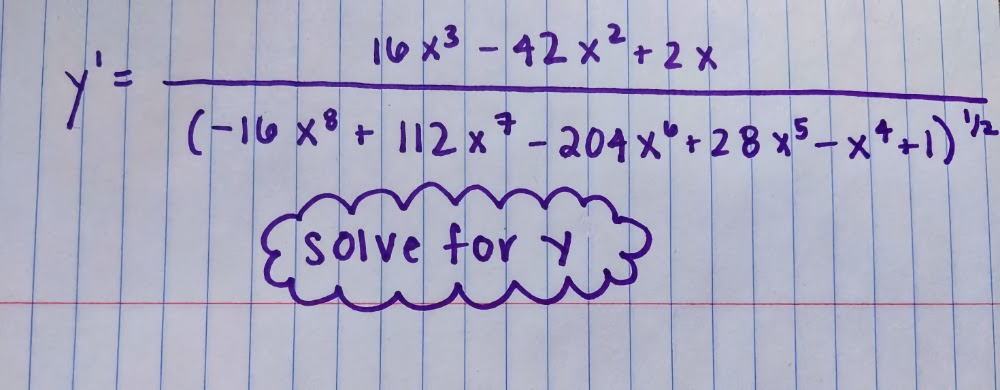 Новая нейросеть может решить это уравнение за одну секунду
Новая нейросеть может решить это уравнение за одну секундуДва исследователя Facebook из Парижа создали для FB новую нейронную сеть, способную решать сложные математические уравнения, даже те, которые имеют дело с математическим анализом. Их работа описана в статье от 2 декабря, опубликованной в архиве arXiv (хранилище научных исследований под управлением Корнельского университета). Это ещё один большой шаг вперёд для нейронных сетей.
Если бы сегодняшние студенты смогли заполучить копию последней нейронной сети Facebook, они могли бы жульничать на протяжении всей третьей части курса математического анализа. Они смогли бы даже решить показанное выше дифференциальное уравнение менее чем за 30 секунд.
Ну, хорошо, возможно, в ближайшее время эта сеть не станет заменой Wolfram Alpha, но в Facebook действительно создали модель, которая может решать сложные математические задачи, а не выполнять простую старую арифметику, с которой модели ИИ обычно имели дело.
Эта работа — огромный скачок в способности компьютеров понимать математическую логику. Исследование изложено в новой статье Deep Learning for Symbolic Mathematics («Глубокое обучение символьной математике»), опубликованной в arXiv. двое парижских учёных, работающих на Facebook, Гийом Лампле и Франсуа Чартон, возглавили поход.
Во введении к своей работе учёные отмечают, что у нейронных сетей нет репутации вундеркиндов, когда дело доходит до вычислений из математического анализа или символического анализа данных — в основном числами, которые вы не можете складывать, умножать или выполнять c ними какие-то иные операции.
«Все данные, используемые компьютерами, являются числами, — рассказывают Лампле и Чартон журналу Популярная механика. — В большинстве случаев они представляют собой такие величины, как интенсивность цвета на изображении или объём продаж продукта. Но иногда числа используются как символы для обозначения объектов или классов. Например, отдельная возрастная группа может быть представлена числом».

«Именно это усложняет для нейронных сетей решение задач с символьными данными, — говорят учёные. — Им нужно изучить как данные, так и символьные правила».
Благодаря уникальному подходу к разбору математической логики компьютеров Лампле и Чартон устранили эту проблему, позволив своей нейронной сети обрабатывать и решать задачи из математического анализа примерно за одну секунду. В своей статье они утверждают, что их нейронная сеть может превзойти другие коммерческие программные пакеты для алгебраических вычислений, такие как Matlab или Wolfram Mathematica, которые профессионалы отрасли обычно используют для вычислений с интегралами.
Зачем нужны дифференциальные уравнения?
На всякий случай, если вы давно изучали математику, напомним: дифференциальное уравнение — это уравнение с одной или несколькими производными некоторой функции. Такие уравнения можно использовать, например, для расчёта скорости изменения быстро увеличивающейся популяции кроликов или, возможно, скорости снижения спроса на конкретную марку кроссовок.
Интегральное уравнение имеет дело с некоторой неизвестной функцией, стоящей под знаком интеграла. Если вы видели фильм Дрянные девчонки и помните, как во время соревнований по математике героиня Линдси Лохан кричала: «Предела не существует!», вы на правильном пути.
Лампле и Чартон рассказывают, что решили сосредоточиться на дифференциальных уравнениях и интегралах по трём основным причинам:
Это сложные задачи, которые часто преподают в университетах и которые трудно решить людям, (оставим машины в стороне).
Проблемы такого рода связаны с манипуляциями с символами, подобными тем, что выполняются в языке. «Поэтому мы подумали, что это хорошая цель для моделей обработки естественного языка, которые мы используем», — говорят они.
Наконец, эти проблемы облегчили двум исследователям создание большого набора задач и решений, чтобы обучить их модель и подтвердить правильность решений.
Проблема с нейронными сетями
В нейронных сетях используется биологический подход к вычислениям, то есть способность решать задачи строится на принципах работы человеческого мозга. Когда мы узнаём новые ассоциации или закономерности, наш мозг выстраивает связи между нейронами. Например, когда вы видите кошку, вы замечаете, что у неё есть мех, два глаза и четыре лапы. При дальнейшем осмотре вы отмечаете, что это маленькое животное. Ваш мозг устанавливает связь: это кошка, а не собака. Всё это время нейроны, обмениваются электрическими сигналами, выстраивая связи между собой. Именно так мы учимся распознавать закономерности.
Точно так же нейронные сети полагаются на слои искусственных «нейронов», которые отражают нейроны в нашем мозгу, только эти так называемые нейроны выполняют базовые вычисления. Когда достаточное количество таких элементов работает вместе, вся сеть может решать более сложные задачи, даже если отдельные её слои настроены на обработку уравнений только одного вида.
Имея это в виду, нейронные сети отлично подходят, чтобы распознавать изображения (пример — квадрат на Facebook, который очерчивает лица друзей чтобы вы могли отметить их); они подходят, чтобы обыгрывать людей в стратегических играх, таких как шахматы или го, или даже помогать автономным автомобилям выявлять потенциальные дорожные опасности, а также прогнозировать поведение барьеров поблизости.
Однако нейронные сети не отличаются способностью решать сложные математические уравнения, например задачи математического анализа. Это потому, что то, как мы узнаём и записываем выражения, выходит за рамки теоретических умов машин.
Разбиение выражений
Нейронным сетям трудно решать уравнения с производными, потому что выражения основаны на условном обозначении, которое имеет смысл для человека, но становится обременительным в смысле компьютеров. Например, мы пишем выражение x³, но в действительности оно означает «x, умноженный на x, умноженный на x». Таким образом, несмотря на простоту, выражения с показателями степени разбиваются на ещё более мелкие и простые математические выражения. Для нейронных сетей эта логика трудна. Она очевидна для людей, но машинам необходимо научиться такой логике.
То же самое верно в задачах дифференциального и интегрального исчисления, где также используются сокращения для более простых уравнений, содержащихся внутри выражения. У этих задач имеются закономерности, которые могут быть обнаружены компьютерными системами, но так уж получилось, что надёжного решения нет до сих пор.
Новый метод Лампле и Чартона включает разбиение сложных выражений на важнейшие составляющие. Затем учёные обучают нейронную сеть находить шаблоны математической логики, которые эквивалентны интегрированию и дифференцированию. Это позволяет программному обеспечению выполнять программу уникальным машинным способом. Затем учёные позволили нейронной сети найти новые выражения, которые не использовались при её обучении, и сравнили результаты с результатами от другого ПО, такого как Wolfram Mathematica и Matlab.
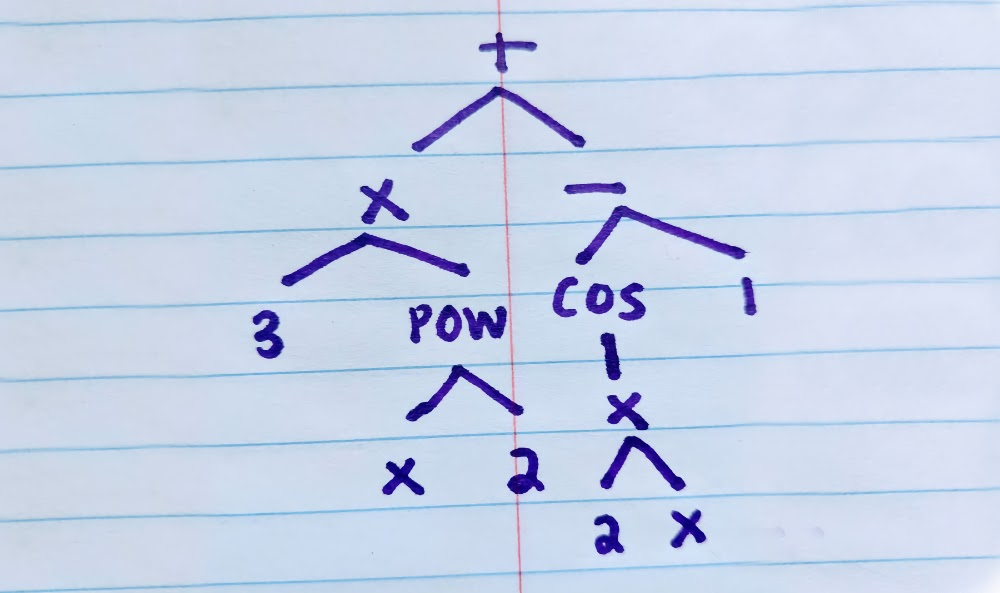
Для этого дуэт разложил уравнения на более мелкие части, представив уравнение в виде дерева. Каждый лист — это число, константа или переменная, а каждый узел — это символ оператора, такой как сложение, умножение, дифференцирование по переменной и так далее.
Например, выражение 2 + 3 x (5 + 2) можно представить следующим образом:

А выражение 3×2 + cos (2x) — 1 разбивается на следующие части:
Обучение нейронной сети
Затем Лампле и Чартону нужно было найти способ обучить свою нейронную сеть, которая должна потреблять огромное количество данных, чтобы установить достаточно широкие связи между своими «нейронами». Эти связи, если они построены правильно, позволяют нейронной сети анализировать дифференциальное уравнение.
Учёные составили случайный набор данных, который включал ряд различных дифференциальных и интегральных задач и их решений. Они сосредоточились на уравнениях первого и второго порядка и ограничили рост выражений. Обработав эти данные, нейронная сеть научилась вычислять производные и интегралы для заданных математических выражений, подобных тому, что показано в начале этой статьи.
Чтобы завершить весь процесс, Лампле и Чартон подвергли нейронную сеть новым испытаниям, скормив ей 5000 новых выражений, которых она никогда раньше не видела. Результаты оказались впечатляющими.
«На всех задачам мы видим, что наша модель значительно превосходит пакет Mathematica, — написали они в своей статье. — При интегрировании функций наша модель достигает точности почти в 100%, тогда как Mathematica едва достигает 85%».
За отведённые 30 секунд Matlab и Mathematica не нашли решения многих задач. Однако нейронной сети Facebook требуется всего лишь секунда, чтобы находить такие решения. Наш пример наверху — одна из таких задач.
Хорошо, что теперь?
К сожалению, в статье Лампле или Чартон нет намёков на то, что в Facebook планируют делать с этой нейронной сетью. Однако, судя по тому, что в их интервью журналу Популярная механика постоянно упоминается обработка естественного языка, вполне возможно, что в Facebook работают над улучшением методов обработки лингвистической информации, которые могут использоваться для множества вещей. Или, может быть, эта гигантская социальная сеть просто хочет помочь вам с домашним заданием? Кто знает.
Лампле и Чартон рассказали журналу Популярная механика что, хотя их модель служит лишь доказательством концепции, она показывает, что нейронные сети могут обрабатывать символьную математику и в своё время появятся практические приложения.
«Дифференциальные уравнения очень распространены в науке, особенно в физике, химии, биологии и технике, поэтому возможно множество приложений», — говорят они.
И, наконец, если вы хотели проверить свое знание математики, вот окончательный ответ, который вы должны были получить, решая уравнение по y в самом первом примере:

Не расстраивайтесь, если вы ошиблись, или если решение заняло у вас гораздо больше времени, чем 30 секунд, которые потребовались нейронной сети Facebook. В конце концов, вы всего лишь человек.
Чтобы быть крутым специалистом, важно не только разбираться в принципах работы классических моделей, но и понимать как это работает и тут понадобится математика. Получить нужные знания и навыки можно на курсе Математика для Data Science или на его расширенной версии Математика и Machine Learning для Data Science.
Узнать, как прокачаться в других специальностях или освоить востребованные профессии с нуля, можно здесь или по ссылкам ниже. Скидка только для хабравчан 50% по промокоду HABR.
Другие профессии и курсыПРОФЕССИИ
КУРСЫ
