[Перевод] Физика Человека-паука с его новыми паутинными крыльями
Врать не буду, я очень жду фильм «Человек-паук: Возвращение домой» [Spider-Man: Homecoming]. А пока что единственной отдушиной для меня будет заняться физикой Человека-паука. И я займусь его новыми паутинными крыльями, увиденными в последнем трейлере.
Для фанатов отмечу, что в некоторых из оригинальных комиксов про Человека-паука действительно было показано, как он их использует, хотя он не всегда использовал их для полётов.
Физика планирования
Что случится после прыжка Человека-паука со здания? Я могу смоделировать его движение, приняв, что на него действуют три силы — гравитация, сопротивление воздуха и подъёмная сила. С вашего позволения, я опишу каждую из них.
• Гравитация — постоянная, направленная вниз сила, пропорциональная массе ЧП (на поверхности Земли, по крайней мере).
• Сопротивление. Представьте, что вы тянете объект через гигантское море шариков для пинг-понга. Замените шарики воздухом — и будет примерно то же самое. Сопротивление увеличивается вместе со скоростью.
• Подъёмная сила. Опять-таки представьте столкновения с шариками, но такие, после которых шарики отскакивают вниз. Заменив шарики воздухом, вы получите подъёмную силу, зависящую от угла атаки, поверхности и скорости.
Вот вам красивая диаграмма сил планирующего на крыльях ЧП. Да, пока мы смоделируем его при помощи треугольника.
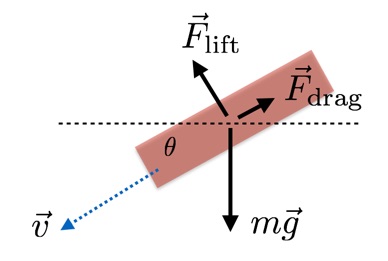
В нашей простой модели подъёмная сила перпендикулярна скорости, а сопротивление направлено в противоположную ей сторону. Для моделирования движения ЧП с крыльями, мне нужна формула для них обеих.
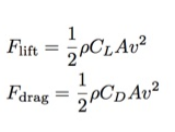
Это величины важных нам сил. Они похожи, за исключением CL (подъёмного коэффициента) и CD (коэффициента сопротивления). В обоих случаях ρ это плотность воздуха (1,2 кг/м3), а v — скорость.
Что есть А? Это площадь поперечного сечения человека (ЧП в нашем случае). По идее, А для сопротивления и для подъёмной силы должны отличаться, в зависимости от угла атаки. Но я не всегда точно знаю, что я делаю — поэтому я сверился с разными источниками, и больше всего к моему случаю подходит статья 2011 года «Траектория падающего Бэтмена» из физического журнала Journal of Physics Special Topics. В ней авторы использовали одну и ту же площадь для сопротивления и подъёмной силы, так что я сделаю то же самое.
Моделирование траектории
Если ЧП спрыгнет со здания, как далеко он сможет сместиться в падении? Какую разницу дадут ему паутинные крылья? Моделировать движение ЧП не так уж просто, поскольку сопротивление и подъёмная сила зависят от скорости. Такую траекторию можно рассчитать только при использовании числовой модели, в которой движение разбивается на небольшие шаги.
Займёмся аппроксимацией. Сначала посчитаем площадь поверхности ЧП. Грубо прикинув, я получил:

Что даёт нам площадь около 0,651 м2 с крыльями и 0,513 м2 без них. Остальные значения:
• Подъёмный коэффициент = 1,45 (значение взято из работы о Бэтмене)
• Коэффициент сопротивления = 0,4 (оттуда же)
• Масса = 64 кг
• Начальная скорость = 8 м/с (горизонтальная)
• И ещё одно предположение: постоянный угол атаки, в связи с чем коэффициенты сопротивления и подъёма не меняются.
Без колебаний я прыгнул в мир числовых моделей. Я оставил в коде комментарии, чтобы вы смогли переделать её для использования в качестве домашней работы.
GlowScript 2.1 VPython
#this is the area with the wings
A1=0.651
#area without wings
A2=0.513
g=vector(0,-9.8,0)
m=64 #mass of Spider-Man
CL=1.45 #coefficient of lift
CD=0.4 #coefficient of drag
rho=1.2 #density of air
#starting velocity
#try changning this
v0=8
#starting momentum assuming horizontal - change this
p=vector(v0,0,0)*m
#p2 is just the momentum for the comparison
p2=p
t=0
dt=0.01
#starting height
h=40
#starting position
r=vector(0,h,0)
r2=r
#these are for the graphs
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
#calculate the velocity to use in lift-drag
v=p/m
v2=p2/m
#calculate the drag force
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
#calculate lift (notice cross product to get direction)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
#total force
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
#update momentum
p=p+F*dt
p2=p2+F2*dt
#update position
r=r+p*dt/m
r2=r2+p2*dt/m
#update time
t=t+dt
#plot stuff
#change this if it makes you happy
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
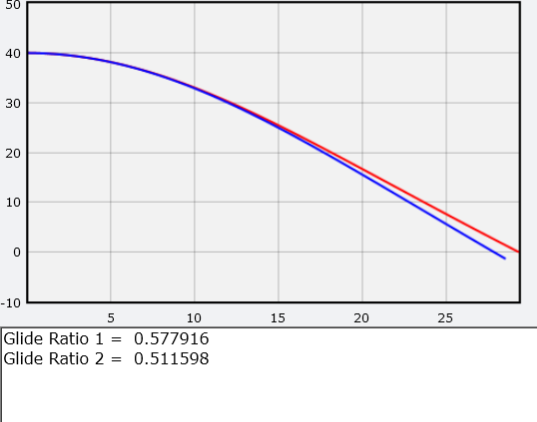
В моей модели красная линия представляет траекторию ЧП с крыльями, а голубая — без крыльев. Также я вывожу значение аэродинамического качества. Поскольку в конце он двигается с постоянной скоростью, это соотношение будет равняться просто отношению х-компоненты импульса, делённой на у-компоненту.
Домашнее заданее
Для ответа на следующие вопросы используйте эту числовую модель. Не волнуйтесь, вы ничего не сломаете. Если что-то сделаете с кодом, просто перезагрузите и начните сначала.
• Согласно Википедии, у прыгающего в крылатом костюме парашютиста аэродинамическое качество (отношение подъёмной силы к лобовому сопротивлению) имеет значение порядка 2,5:1 (то есть, наша программа вывела бы число 2,5). Сможете ли вы так подправить код, чтобы программа выдала такое значение? Подсказка: меняйте как площадь поверхности, так и начальную скорость.
• Что, если ЧП упадёт вертикально вниз? Какую предельную скорость он приобретёт с крыльями, и без них?
• Как быстро ЧП нужно двигаться по горизонтали, чтобы он полетел вверх, а не вниз, в начале полёта?
• Может ли ЧП прыгнуть, целясь вниз, так, чтобы набрать большую скорость и на какое-то время перейти в горизонтальный полёт?
• Можете ли вы построить улучшенную модель, принимающую во внимание угол атаки? Возможно, и сможете, но мне кажется, что полёты с малой скоростью — достаточно сложная тема.
