[Перевод] Дротики, кости и монеты: алгоритмы выборки из дискретного распределения14.08.2018 13:18

Однажды я задал на Stack Overflow вопрос о структуре данных для шулерских игральных костей. В частности, меня интересовал ответ на такой вопрос: «Если у нас есть n-гранная кость, у грани которой i есть вероятность выпадения pi. Какова наиболее эффективная структура данных для симуляции бросков такой кости?»

Такую структуру данных можно использовать для многих задач. Например, можно применять её для симуляции бросков честной шестигранной кости, присвоив вероятность $\frac{1}{6}$ каждой из сторон кости, или для симуляции честной монетки имитацией двусторонней кости, вероятность выпадения каждой из сторон которой равна $\frac{1}{2}$ . Также можно использовать эту структуру данных для непосредственной симуляции суммы двух честных шестигранных костей, создав 11-гранную кость (с гранями 2, 3, 4, …, 12), каждая грань которой имеет вес вероятности, соответствующий броскам двух честных костей. Однако можно также использовать эту структуру данных и для симуляции шулерских костей. Например, если вы играете в «крэпс» с костью, которая, как вы точно знаете, не идеально честная, то можно использовать эту структуру данных для симуляции множества бросков костей и анализа оптимальной стратегии. Также можно попробовать симулировать аналогичным образом неидеальное колесо рулетки.

Если выйти за пределы игр, то можно применить эту структуру данных в симуляции роботов, датчики которых имеют известные уровни отказа. Например, если датчик дальности имеет 95-процентную вероятность возврата правильного значения, 4-процентную вероятность слишком маленького значения, и 1-процентную вероятность слишком большого значения, то можно использовать эту структуру данных для симуляции считывания показаний датчика генерацией случайного результата и симуляцией считывания датчиком этого результата.
Полученный мной в Stack Overflow ответ впечатлил меня по двум причинам. Во-первых, в решении мне посоветовали использовать мощную технику под названием alias-метод, которая при определённых разумных предположениях о модели машины способна после простого этапа предварительной подготовки симулировать броски кости за время $O(1)$ . Во-вторых, меня ещё больше удивило то, что этот алгоритм известен в течение десятков лет, но мне он ни разу не встречался! Учитывая то, сколько вычислительного времени тратится на симуляцию, можно было бы ожидать, что эта техника известна гораздо шире. Несколько запросов в Google дали мне множество информации об этой технике, но я не смог найти ни единого сайта, где бы соединились вместе интуитивное понимание и объяснение этой техники.

Эта статья является моей попыткой сделать краткий обзор различных подходов к симуляции шулерской кости, от простых и очень непрактичных техник, до очень оптимизированного и эффективного alias-метода. Я надеюсь, что мне удастся передать различные способы интуитивного понимания задачи и то, насколько каждый из них подчёркивает какой-то новый аспект симуляции шулерской кости. Моя цель для каждого подхода заключается в исследовании мотивирующей идеи, базового алгоритма, доказательства верности и анализа времени выполнения (с точки зрения требуемых времени, памяти и случайности).

Вступление

Прежде чем переходить к конкретным подробностям различных техник, давайте сначала стандартизируем терминологию и систему обозначений.

Во введении к статье я использовал термин «шулерская кость» для описания обобщённого сценария, в котором существует конечное множество результатов, с каждым из которых связана вероятность, Формально это называется дискретным распределением вероятностей, а задача симуляции шулерской кости называется выборкой из дискретного распределения.

Для описания нашего дискретного распределения вероятностей (шулерской кости) мы будем считать, что у нас есть множество из n вероятностей $p_0, p_1, ..., p_{n - 1}$ , связанных с результатами $0, 1, ..., n - 1$ . Хотя результаты могут быть любыми (орёл/решка, числа на костях, цвета и т.д.), для простоты я буду считать результат каким-то положительным вещественным числом, соответствующим заданному индексу.

Работа с вещественными числами на компьютере — это «серая область» вычислений. Существует множество быстрых алгоритмов, скорость которых обеспечивается исключительно способностью за постоянное время вычислять функцию floor произвольного вещественного числа, и численные неточности в представлении чисел с плавающей запятой могут полностью разрушить некоторые алгоритмы. Следовательно, прежде чем приступать к каким-либо обсуждениям алгоритмов, работающих с вероятностями, то есть вступать в тёмный мир вещественных чисел, я должен уточнить, что может и чего не может компьютер.

Здесь и далее я буду предполагать, что все указанные ниже операции могут выполняться за постоянное время:

Сложение. вычитание, умножение, деление и сравнение произвольных вещественных чисел. Нам необходимо будет это делать для манипуляций с вероятностями. Может показаться, что это слишком смелое предположение, но если считать, что точность любого вещественного числа ограничена неким многчленом размера слова машины (например, 64-битное double на 32-битной машине), но я не думаю, что это слишком неразумно.
Генерирование равномерного вещественного числа в интервале [0, 1). Для симуляции случайности нам нужен некий источник случайных значений. Я предполагаю, что мы можем за постоянное время генерировать вещественное число произвольной точности. Это намного превышает возможности реального компьютера, но мне кажется, что в целях этого обсуждения такое допустимо. Если мы согласимся пожертвовать долей точности, сказав, что произвольное IEEE-754 double находится в интервале [0, 1], то мы и в самом деле потеряем точность, но результат, вероятно, будет достаточно точным для большинства применений.
Вычисление целочисленного floor (округления в меньшую сторону) вещественного числа. Это допустимо, если мы предположим, что работаем с IEEE-754 double, но в общем случае такое требование к компьютеру невыполнимо.

Стоит задаться вопросом — разумно ли считать, что мы можем выполнять все эти операции эффективно. На практике мы редко используем вероятности, указываемые до такого уровня точности, при котором свойственная IEEE-754 double ошибка округления может вызвать серьёзные проблемы, поэтому выполнить все представленные выше требования мы можем, просто работая исключительно с IEEE double. Однако если мы находимся в среде, где вероятности указываются точно как рациональные числа высокой точности, то подобные ограничения могут оказаться неразумными.

Симуляция честной кости

Прежде чем мы перейдём к более общему случаю бросания произвольной шулерской кости, давайте начнём с более простого алгоритма, который послужит строительным блоком для последующих алгоритмов: с симуляции честной n-гранной кости. Например, нам могут пригодиться броски честной 6-гранной кости при игре в Monopoly или Risk, или бросание честной монетки (двусторонней кости) и т.д.

Для этого конкретного случая есть простой, элегантный и эффективный алгоритм симуляции результата. В основе алгоритма лежит следующая идея: предположим, что мы можем генерировать действительно случайные, равномерно распределённые вещественные числа в интервале $[0, 1)$ . Проиллюстрировать этот интервал можно следующим образом:

Теперь если мы хотим бросить $n$ -гранную кость, то один из способов заключается в разделении интервала $[0, 1)$ на $n$ областей равного размера, каждая из которых имеет длину $\frac{1}{n}$ . Это выглядит следующим образом:

Далее мы генерируем случайно выбираемое вещественное число в интервале $[0, 1)$ , которое точно попадает в одну из этих маленьких областей. Из этого мы можем считать результат броска кости, посмотрев на область, в которую попало число. Например, если наше случайно выбранное значение попало в это место:

то мы можем сказать, что на кости выпало 2 (если считать, что грани кости проиндексованы с нуля).

Графически легко увидеть, в какую из областей попало случайное значение, но как нам закодировать это в алгоритме? И здесь мы воспользуемся тем фактом, что это честная кость. Поскольку все интервалы имеют равный размер, а именно $\frac{1}{n}$ , то мы можем увидеть, какое наибольшее значение $i$ является таким, что $\frac{i}{n}$ не больше случайно сгенерированного значения (назовём это значение x). Можно заметить, что если мы хотим найти максимальное значение, такое, что $\frac{i}{n} \le x$ , то это аналогично нахождению максимального значения $n$ , такого, что $i \le xn$ . Но это по определению означает, что $i = \lfloor xn \rfloor$ , наибольшее натуральное число не больше xn. Следовательно, это приводит нас к такому (очень простому) алгоритму симуляции честной n-гранной кости:

Алгоритм: симуляция честной кости

Генерируем равномерно распределённое случайное значение в интервале .

Возвращаем $\lfloor xn \rfloor$ .

Учитывая наши сделанные выше допущения о вычислениях, этот алгоритм выполняется за время .

Из этого раздела можно сделать два вывода. Во-первых, мы можем разделить интервал $[0, 1)$ на части так, что равномерно распределённое случайное вещественное число в этом интервале естественным образом сводится к одному из множества доступных нам дискретных вариантов. В оставшейся части статьи мы активно будем эксплуатировать эту технику. Во-вторых, может быть сложно определить, к какому конкретно интервалу относится случайное значение, но если мы знаем что-то о частях (в этом случае — что они все одинакового размера), то можно математически просто определить, к какой именно части относится конкретная точка.

Симуляция шулерской кости при помощи честной кости

Имея алгоритм симуляции честной кости, можем ли мы адаптировать его для симуляции шулерской кости? Интересно, что ответ положительный, но решение потребует больше пространства.

Из предыдущего раздела интуитивно понятно, что для симуляции броска шулерской кости нам достаточно разделить интервал $[0, 1)$ на части, а затем определить, в какую часть мы попали. Однако в общем случае это может оказаться гораздо сложнее, чем кажется. Допустим, у нас есть четырёхгранная кость с вероятностями граней $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{12}$ и $\frac{1}{12}$ (мы можем убедиться, что это правильное распределение вероятностей, ведь $\frac{1}{2} + \frac{1}{3} + \frac{1}{12} + \frac{1}{12} = \frac{6}{12} + \frac{4}{12} + \frac{1}{12} + \frac{1}{12} = \frac{12}{12}$ ). Если мы разделим интервал $[0, 1)$ на четыре части этих размеров, то получим следующее:

К сожалению, на этом шаге мы застрянем. Даже если бы мы знали случайное число в интервале $[0, 1)$ , то не существует простых математических трюков, позволяющих автоматически определить, в какую часть попало это число. Я не хочу сказать, что это невозможно — как вы увидите, мы можем использовать множество отличных трюков —, но ни один из них не имеет математической простоты алгоритма броска честной кости.

Однако мы можем адаптировать технику, используемую для честной кости, чтобы она работала и в этом случае. Давайте возьмём для примера рассмотренную выше кость. Вероятность выпадения граней равна $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{12}$ и $\frac{1}{12}$ . Если мы перепишем это так, чтобы у всех членов был общий делитель, то получим значения $\frac{6}{12}$ , $\frac{4}{12}$ , $\frac{1}{12}$ и $\frac{1}{12}$ . Поэтому мы можем воспринимать эту задачу следующим образом: вместо бросков четырёхгранной кости с взвешенными вероятностями почему бы нам не бросать 12-гранную честную кость, на гранях которой есть повторяющиеся значения? Поскольку мы знаем, как симулировать честную кость, это будет аналогом разделения интервала $[0, 1)$ на части таким образом:

Тогда мы назначим их различным результатам следующим образом:

Теперь симулировать бросок кости будет очень просто — мы просто бросаем эту новую честную кость, а затем смотрим, какая грань выпала и считываем её значение. Этот первый шаг можно выполнить представленным выше алгоритмом, что даст нам целое числов в интервале $0, 1, ..., 11$ . Чтобы привязать это целое число к одной из граней исходной шулерской кости, мы будем хранить вспомогательный массив из двенадцати элементов, связывающих каждое из этих чисел с исходным результатом. Графически это можно изобразить так:

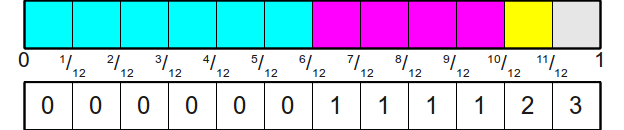
Чтобы формализировать это в виде алгоритма, мы опишем и этап инициализации (получение таблицы), и этап генерации (симуляцию броска случайной кости). Оба эти этапа важно учитывать в этом и последующих алгоритмах, потому что время подготовки должно быть отличным.

На этапе инициализации мы начинаем с поиска наименьшего общего кратного всех вероятностей, заданных для граней кости (в нашем примере НОК равно 12). НОК полезно здесь, потому что оно соответствует наименьшему общему делителю, который мы можем использовать для всех дробей, а значит, и количеству граней новой честной кости, которую мы будем бросать. Получив это НОК (обозначим его L), мы должны определить, сколько граней новой кости будет распределено на каждую из граней исходной шулерской кости. В нашем примере грань с вероятностью $\frac{1}{2}$ получает шесть сторон новой кости, поскольку $\frac{1}{2} \times 12 = 6$ . Аналогичным образом, сторона с вероятностью $\frac{1}{3}$ получает 4 грани, поскольку $\frac{1}{3} \times 12 = 4$ . В более обобщённом виде, если L является НОК вероятностей, а $p_i$ является вероятностью выпадения грани $i$ кости, то мы выделим грани $i$ исходной шулерской кости $L \cdot p_i$ граней честной кости.

Вот псевдокод представленного выше алгоритма:

Алгоритм: симуляция шулерской кости при помощи честной кости

Возможно, этот алгоритм и прост, но насколько он эффективен? Само генерирование бросков кости достаточно быстрое — каждый бросок кости требует $O(1)$ времени работы для генерирования случайного броска кости с помощью предыдущего алгоритма, плюс ещё $O(1)$ времени работы на поиск по таблице. Это даёт нам общее время работы $O(1)$ .

Однако этап инициализации может быть чрезвычайно затратным. Чтобы этот алгоритм заработал, нам нужно выделить пространство под массив размером с НОК знаменателей всех входных дробей. В нашем примере ( $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{12}$ , $\frac{1}{12}$ ), он равен 12, для при других входных значениях значения могут быть патологически плохими. Например, давайте рассмотрим дроби $\frac{999999}{1000000}$ и $\frac{1}{1000000}$ . НОК знаменателей равен миллиону, поэтому в нашей таблице должен быть один миллион элементов!

К сожалению, всё может быть ещё хуже. В предыдущем примере мы по крайней мере можем «ожидать», чтоб алгоритм займёт много памяти, поскольку оба знаменателя дробей равны одному миллиону. Однако у нас может появиться множество вероятностей, для которых НОК значительно больше, чем каждый отдельный знаменатель. Для примера давайте рассмотрим вероятности $\frac{1}{15}$ , $\frac{1}{10}$ , $\frac{5}{6}$ . Здесь НОК знаменателей равно 30, что больше, чем любой из знаменателей. Конструкция здесь работает, потому что $15 = 3 \times 5$ , $10 = 2 \times 5$ , а $6 = 2 \times 3$ ; другими словами, каждый знаменатель является произведением двух простых чисел, выбранного из пула трёх значений. Поэтому их НОК является произведением всех этих простых чисел, поскольку каждый знаменатель должен являться делителем НОК. Если мы обобщим эту конструкцию и рассмотрим любое множество из $k$ простых чисел и возьмём одну дробь для каждого из попарных произведений этих простых чисел, то НОК будет гораздо больше, чем каждый отдельный знаменатель. На самом деле, одним из наилучших верхних границ, которые мы можем получить для НОК, будет $O(\prod_{i = 0}^n{d_i})$ , где $d_i$ — это знаменатель $i$ -той вероятности. Это не позволяет использовать такой алгоритм в реальных условиях, когда вероятности неизвестны заранее, поскольку память, необходимая для хранения таблицы размера $O(\prod_{i = 0}^n{d_i})$ , может запросто оказаться больше объёма, способного поместиться в ОЗУ.

Иными словами, во многих случаях этот алгоритм ведёт себя хорошо. Если все вероятности одинаковы, то все получаемые на входе вероятности равны $\frac{1}{n}$ для какого-то $n$ . Тогда НОК знаменателей равно $n$ , то есть в результате бросаемая честная кость будет иметь $n$ граней, и каждая грань исходной кости будет соответствовать одной грани честной кости. Следовательно, время инициализации равно $O(n)$ . Графически это можно изобразить так:

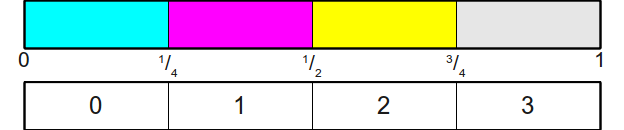
Это даёт нам следующую информацию об алгоритме:
Ещё одна важная подробность об этом алгоритме: он предполагает, что мы будем получать удобные вероятности в виде дробей с хорошими знаменателями. Если вероятности задаются как IEEE-754 double, то такой подход скорее всего ждёт катастрофа из-а небольших ошибок округления; представьте, что у нас есть вероятности 0,25 и 0,250000000001! Поэтому такой подход, вероятно, лучше не использовать, за исключением особых случаев, когда вероятности ведут себя хорошо и указаны в формате, соответствующем операциям с рациональными числами.

Симуляция несимметричной монеты

Наше объяснение простого случайного примитива (честной кости) привело к простому, но потенциально ужасно неэффективному алгоритму симуляции шулерской кости. Возможно, изучение других простых случайных примитивов прольёт немного света на другие подходы к решению этой задачи.

Простая, но на удивление полезная задача заключается в симуляции с помощью генератора случайных чисел несимметричной монеты. Если у нас есть монета с вероятностью выпадения орла $p_{heads}$ , то как мы можем симулировать бросок такой несимметричной монеты?

Ранее мы выработали один интуитивно понятный подход: разбиение интервала $[0, 1)$ на последовательность таких областей, что при выборе случайного значения в интервале оно оказывается в какой-то области с вероятностью, равной размеру области. Для симуляции несимметричной монеты с помощью равномерно распределённого случайного значения в интервале $[0, 1)$ мы должны разбить интервал следующим образом:

А потом сгенерировать равномерно распределённое случайное значение в интервале $[0, 1)$ , чтобы посмотреть, в какой области оно содержится. К счастью, точка разбиения у нас только одна, поэтому очень легко определить, в какой области находится точка; если значение меньше $p_{heads}$ , то на монете выпал орёл, в противном случае — решка. Псевдокод:

Алгоритм: симуляция несимметричной монеты

Генерируем равномерно распределённое случайное значение в интервале .

Если $x < p_{heads}$ , возвращаем «орёл».

Если $x \ge p_{heads}$ , возвращаем «решка».

Поскольку мы можем сгенерировать равномерно распределённое случайное значение в интервале $[0, 1)$ за время $O(1)$ , а также можем выполнить сравнение вещественных чисел тоже за $O(1)$ , то этот алгоритм выполняется за время $O(1)$ .

Симуляция честной кости с помощью несимметричных монет

Из предыдущего обсуждения мы знаем, что можно симулировать шулерскую кость с помощью честной кости, если предположить, что мы готовы потратить лишнее место в памяти. Поскольку мы можем воспринимать несимметричную монету как шулерскую двустороннюю кость, то это значит, что мы можем симулировать несимметричную монету с помощью честной кости. Интересно, что можно сделать и обратное — симулировать честную кость с помощью несимметричной монеты. Конструкция получается простой, элегантной и её можно легко обобщить для симуляции шулерской кости с помощью множества несимметричных монет.

Конструкция для симуляции несимметричной монеты разбивает интервал $[0, 1)$ на две области — область «орлов» и область «решек» на основании вероятности выпадения на кости орлов. Мы уже видели подобный трюк, использованный для симуляции честной $n$ -гранной кости: интервал $[0, 1)$ делился на $n$ равных областей. Например, при броске четырёхгранной кости у нас получалось следующее разделение:

Теперь предположим, что нас интересует симуляция броска этой честной кости с помощью набора несимметричных монет. Один из способов решения заключается в следующем: представьте, что мы обходим эти области слева направо, каждый раз спрашивая, хотим ли мы останавливаться в текущей области, или будем двигаться дальше. Например, давайте предположим, что мы хотим выбрать случайным образом одну из этих областей. Начиная с самой левой области, мы будем подбрасывать несимметричную монету, которая сообщает нам, должны ли мы остановиться в этой области, или продолжить движение дальше. Поскольку нам нужно выбирать из всех этих областей равномерно с вероятностью $\frac{1}{4}$ , то мы можем сделать это, подбрасывая несимметричную монету, орлы на которой выпадают с вероятностью $\frac{1}{4}$ . Если выпадает орёл, то мы останавливаемся в текущей области. В противном случае мы двигаемся в следующую область.

Если монеты падают решкой вверх, то мы оказывается во второй области и снова спрашиваем, должны ли мы снова выбрать эту область или продолжать движение. Вы можете подумать, что для этого мы должны бросить ещё одну монету с вероятностью выпадения орла $\frac{1}{4}$ , но на самом деле это неверно! Чтобы увидеть недостаток в этом рассуждении, мы должны дойти до крайней ситуации — если в каждой области мы бросаем монету, на которой выпадает орёл с вероятностью $\frac{1}{4}$ , то есть небольшая вероятность, что в каждой области монета выпадет решкой, то есть нам придётся отказаться от всех областей. При движении по областям нам каким-то образом нужно продолжать увеличивать вероятность выпадения на монете орла. В крайней ситуации, если мы окажемся в последней области, то на монете должен быть орёл с вероятностью $1$ , поскольку если мы отклонили все предыдущие области, то правильным решением будет остановиться в последней области.

Чтобы определить вероятность, с которой наша несимметричная монета должна выбрасывать орла после пропуска первой области, нам нужно заметить, что после пропуска первой области их осталось всего три. Поскольку мы бросаем честную кость, нам нужно, чтобы каждая из этих трёх областей была выбрана с вероятностью $\frac{1}{3}$ . Следовательно, интуитивно кажется, что у нас должна быть вторая кость, на которой выпадает орёл с вероятностью $\frac{1}{3}$ . Используя аналогичные рассуждения, можно понять, что при выпадании во второй области решки в третьей области монета должна выпадать орлом с вероятностью $\frac{1}{2}$ , а в последней области — с вероятностью $1$ .

Такое интуитивное понимание приводит нас к следующему алгоритму. Заметьте, что мы не обсуждали правильность или ошибочность этого алгоритма; вскоре мы этим займёмся.

Алгоритм: симуляция честной кости с помощью несимметричных монет

For to :
Бросаем несимметричную монету с вероятностью выбрасывания орла $\frac{1}{n - i}$ .

Если выпадает орёл, то возвращаем .

Этот алгоритм прост и в наихудшем случае выполняется за время $O(n)$ . Но как нам проверить, правилен ли он? Чтобы узнать это, нам потребуется следующая теорема:

Теорема: приведённый выше алгоритм возвращает сторону с вероятностью $\frac{1}{n}$ для любого выбранного .
Доказательство: рассмотрим любое постоянное $n \ge 0$ . Мы доказываем с помощью сильной индукции, что каждая из граней имеет вероятность выбора $\frac{1}{n}$ .
Для нашего примера мы показываем, что грань кости имеет вероятность выбора $\frac{1}{n}$ . Но это непосредственно следует из самого алгоритма — мы выбираем грань 0, если на несимметричной монете с вероятностью выпадения орла $\frac{1}{n}$ выпадает орёл, то есть мы выбрали её с вероятностью $\frac{1}{n}$ .
Для этапа индукции предположим для граней , что эти грани выбираются с вероятностью $\frac{1}{n}$ и рассмотрим вероятность выбора грани . Грань будет выбрана тогда и только тогда, когда не выбраны первые граней, а на монете с вероятностью выпадения орла $\frac{1}{n - k}$ выпал орёл. Поскольку каждая из первых граней имеет вероятность выбора $\frac{1}{n}$ , и поскольку выбирается только одна грань, то вероятность выбора одной из первых граней задаётся как $\frac{k}{n}$ . Это значит, что вероятность того, что алгоритм не выберет одну из первых граней равен $1 - \frac{k}{n} = \frac{n}{n} - \frac{k}{n} = \frac{n - k}{n}$ . То есть вероятность выбора грани задаётся как $\frac{n - k}{n} \frac{1}{n - k} = \frac{1}{n}$ , что и требуется показать. Таким образом, каждая грань кости выбирается равномерно и случайно.

Разумеется, алгоритм довольно неэффективен — с помощью первой техники мы можем симулировать бросок честной кости за время $O(1)$ ! Но этот алгоритм можно использовать как ступеньку к достаточно эффективному алгоритму симуляции шулерской кости с помощью несимметричных монет.

Симуляция шулерской кости с помощью несимметричных монет

Представленный выше алгоритм интересен тем, что даёт нам простой каркас для симуляции кости с помощью набора монет. Мы начинаем с броска монеты для определения того, нужно ли выбрать первую грань кости или двигаться к оставшимся. При этом процессе нам нужно внимательно обращаться с изменением масштаба оставшихся вероятностей.

Давайте посмотрим, как можно использовать эту технику для симуляции броска шулерской кости. Воспользуемся нашим примером с вероятностями $\frac{1}{2}$ , $\frac{1}{3}$ , $\frac{1}{12}$ , $\frac{1}{12}$ . Он, если вы не помните, делит интервал $[0, 1)$ следующим образом: