[Из песочницы] Пробуем q-learning на вкус, повесть в трех частях27.12.2017 10:33

Эта статья — небольшая заметка о реализации алгоритма q-learning для управления агентом в стохастическом окружении. Первая часть статьи будет посвящена созданию окружения для проведения симуляций — мини-игр на поле nxn, в которых агент должен как можно дольше продержаться на удалении от противников, движущихся случайным образом. Задача противников, соответственно, его настигнуть. Очки начисляются за каждый ход, проведенный агентом в симуляции. Вторая часть статьи затронет основы q-learning алгоритма и его имплементацию. В третьей части попробуем поменять параметры, которые определяют восприятие окружения агентом. Проанализируем влияние этих параметров на результативность его игры. Акцент я специально сместил в сторону использования минимального количества сторонних модулей. Цель — прикоснуться к самой сути алгоритма, так сказать потрогать руками. Для реализации будем использовать только «pure» python 3.

vq3pweivudxkrs174pjfyblkz1o.png

Часть 1. Создание окружения


Среда, в которой действует агент, представлена двумерным полем размера n. Вот так оно выглядит:

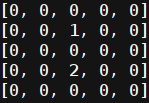
qgrzga4p-7ff8zbtaa2ikvly9nu.png

Здесь единицей представлен агент, двойкой обозначен противник. Теперь обратимся непосредственно к коду. Переменные, которые описывают окружение: размер поля, агент, список противников.

класс окружения
class W:
    def __init__(self,n):
        self.n=n
        self.P=P(1,1,n) 
        self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)]


Типовой актор: агент или противник.

класс актора
class un:
    def __init__(self,x,y):
        self.x = x
        self.y = y
    def getxy(self):
        return self.x, self.y


Описание aгента.

класс агента
class P(un):
    def __init__(self,x,y,n):
        self.n=n
        un.__init__(self,x,y)


Стратегия агента, пока пустая.

метод, вызывающий стратегию агента
    def strtg(self):
        return 0,0


Каждый из участников симуляции может совершать ход в любом направлении, в том числе по диагонали, актор также может не перемещаться вовсе. Набор разрешенных движений на примере противника:

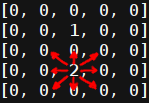
_zoru301wup_vguipugrztozg1c.png

Благодаря движениям по диагонали противник всегда имеет возможность настигнуть агента, как бы тот ни старался уйти. Это обеспечивает конечное количество ходов симуляции для любой степени обученности агента. Запишем его возможные действия с проверкой валидности смещения. Метод принимает изменение координат агента и обновляет его положение.

метод хода агента
    def move(self):
        dx,dy=self.strtg()
        a=self.x+dx
        b=self.y+dy
        expr=((0<=a


Описание противника.

класс противника
class EN(un):
    def __init__(self,x,y,n):
        self.n=n
        un.__init__(self,x,y)


Перемещение противника с проверкой допустимости смещения. Метод не выходит из цикла до тех пор, пока не удовлетворено условие валидности хода.

метод хода противника
    def move(self):
        expr=False
        while not expr:
            a=self.x+random.choice([-1,0,1])
            b=self.y+random.choice([-1,0,1])
            expr=((0<=a


Один шаг симуляции. Обновление позиции противника и агента.

метод окружения, разворачивает последующий шаг симуляции
    def step(self):
        for i in self.ens:
            i.move()
        self.P.move()


Визуализация работы симуляции.

метод окружения, отрисовка поля и положения акторов
    def pr(self):
        print('\n'*100)
        px,py=self.P.getxy()
        self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)])
        self.wmap[py][px]=1
        for i in self.ens:
            ex,ey=i.getxy()
            self.wmap[ey][ex]=2
        for i in self.wmap:
            print(i)


Симуляция, основные этапы:

1. Регистрация координат акторов.
2. Проверка достижения условий завершения симуляции.
3. Старт цикла обновления ходов симуляции.
 — Отрисовка окружения.
 — Обновление состояния симуляции.
 — Регистрация координат акторов.
 — Проверка достижения условий завершения симуляции.
4. Отрисовка окружения.

метод окружения, воспроизведение последовательности симуляции
    def play(self):
        px,py=self.P.getxy()
        bl=True
        for i in self.ens:
            ex,ey=i.getxy()
            bl=bl and (px,py)!=(ex,ey)
        iter=0
        while bl:
            time.sleep(1)
            wr.pr()
            self.step()
            px,py=self.P.getxy()
            bl=True
            for i in self.ens:
                ex,ey=i.getxy()
                bl=bl and (px,py)!=(ex,ey)
                print((px,py),(ex,ey))
            print('___')
            iter=iter+1
        print(iter)


Инициализация окружения и запуск.

запуск симуляции
if __name__=="__main__":
    wr=W(7)
    wr.play()
    wr.pr()


Часть 2. Обучение агента


Метод q-learning основан на введении функции Q, отражающей ценность каждого возможного действия a агента для текущего состояния s, в котором сейчас находится симуляция. Или коротко:

$Q(s,a)$

Эта функция задает оценку агентом той награды, которую он может получить, совершив в определенный ход определенное действие. А также она включает в себя оценку того, какую награду агент может получить в будущем. Процесс обучения представляет из себя итерационное уточнение значения функции Q на каждом ходу агента. В первую очередь следует определить величину награды, которую агент получит в этот ход. Запишем ее переменной $r_t$. Далее определим величину максимальной ожидаемой награды на последующих ходах:

$\max_{a}Q(s_{t+1},a)$

Теперь следует решить, что для агента имеет большую ценность: сиюминутные награды или будущие. Данная проблема разрешается дополнительным коэффициентом при составляющей оценки последующих наград. В итоге предсказываемая агентом величина функции Q на данном шаге должна быть максимально приближена к значению:

$r_t+\gamma \cdot \max_{a}Q(s_{t+1},a)$

Таким образом, ошибка предсказания агентом значения функции Q для текущего хода запишется следующим образом:

$\Delta q=r_t+\gamma \cdot \max_{a}Q(s_{t+1},a)-Q(s_t,a_t)$

Введем коэффициент, который будет регулировать скорость обучения агента. Тогда формула для итерационного расчета функции Q имеет вид:

$Q(s_{t+1},a_{t+1})=Q(s_t,a_t)+\alpha \cdot\Delta q$

Общая формула итерационного расчета функции Q:

$Q(s_{t+1},a_{t+1})=Q(s_t,a_t)+\alpha \cdot(r_t+\gamma \cdot \max_{a}Q(s_{t+1},a)-Q(s_t,a_t))$

Выделим основные признаки, которые будут составлять описание окружения с точки зрения агента. Чем обширнее набор параметров, тем точнее его реакция на изменения среды. В то же время размер пространства состояний может существенно влиять на скорость обучения.

метод агента, признаки, описывающие состояние окружения
    def get_features(self,x,y):
        features=[]
        for i in self.ens: #800-1400
          ex,ey=i.getxy()
          features.append(ex)
          features.append(ey)
        features.append(x)
        features.append(y)
        return features


Создание класса Q модели. Переменная gamma — коэффициент затухания, позволяющий нивелировать вклад последующих наград. Переменная alpha — коэффициент скорости обучения модели. Переменная state — словарь состояний модели.

класс Q модели
class Q:
    def __init__(self):
        self.gamma=0.95
        self.alpha=0.05
        self.state={}


Получим состояние агента в данный ход.

метод Q модели, по запросу получает состояние агента
    def get_wp(self,plr):
        self.plr=plr


Тренируем модель.

метод Q модели, один этап обучения модели
    def run_model(self,silent=1):
        self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy)
        self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+(
                            self.plr.dx,self.plr.dy)

        if not silent:
            print(self.plr.prev_state)
            print(self.plr.curr_state)

        r=self.plr.reward   

        if self.plr.prev_state not in self.state:
            self.state[self.plr.prev_state]=0
        
        nvec=[]
        for i in self.plr.actions:
            cstate=self.plr.curr_state[:-2]+(i[0],i[1])
            if cstate not in self.state:
                self.state[cstate]=0
            nvec.append(self.state[cstate])

        nvec=max(nvec)
        self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*(-self.state[self.plr.prev_state]+r+self.gamma*nvec)


Метод получения наград. Агенту присваевается награда за продолжение симуляции. Штраф зачисляется за коллизию с противником.

метод окружения, определение размера наград
    def get_reward(self,end_bool):
        if end_bool:
            self.P.reward=1
        else:
            self.P.reward=-1


Стратегия агента. Производит выбор наилучшего значения из словаря состояний модели. Классу агента добавлена переменная eps, вносящая элемент случайности при выборе хода. Это делается для изучения смежных возможных действий в данном состоянии.

метод агента, выбор следующего хода
    def strtg(self):
        if random.random()


Покажем, чему удалось научиться агенту при полной передаче информации о состоянии симуляции (абсолютные координаты агента, абсолютные координаты противника):

результат работы алгоритма (гифка ~1Мб)
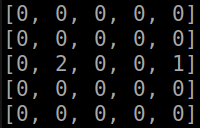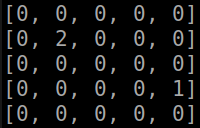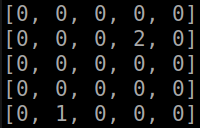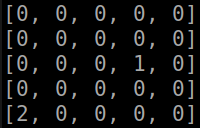
u6um3qykqygci2q5a1bxafqpjde.gif


Часть 3. Варьируем параметры, отражающие состояние окружения для агента


Для начала рассмотрим ситуацию, когда агенту не поступает вообще никакой информации об окружении.

features 1
    def get_features(self,x,y):
        features=[]
        return features


В результате работы такого алгоритма агент набирает в среднем 40–75 очков за одну симуляцию. График обучения:

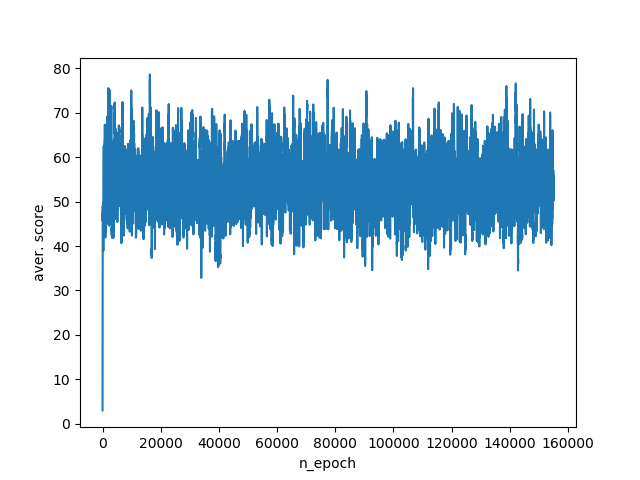
bygnf0f8v4jnes6xzwimgjzvreq.png

Добавим агенту данных. В первую очередь необходимо знать, как далеко находится противник. Вычислим это используя евклидово расстояние. Также важно иметь представление насколько близко агент подошел к кромке.

features 2
    def get_features(self,x,y):
        features=[]
        for i in self.ens: 
            ex,ey=i.getxy()
            dx=abs(x-ex)
            dy=abs(y-ey)
            l=hypot(dx,dy)
            features.append(l)
        to_brdr=min(x,y,self.n-1-x,self.n-1-y)
        features.append(to_brdr)
        return features


Учет этой информации поднимает нижние показатели агента на 20 очков за симуляцию и его средний счет становится в пределах 60–100 баллов. Несмотря на то, что реакция на изменения в окружении улучшилась, мы все еще теряем львиную долю необходимых данных. Так, агент до сих пор не знает, в какую сторону нужно двигаться, чтобы разорвать дистанцию с противником или отойти от края кромки. График обучения:

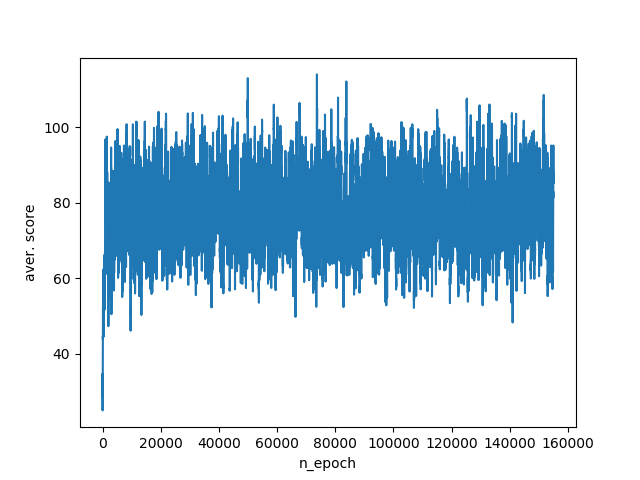
02r0og-v-mofewifzfrkzqfe_sw.png

Следующий этап — добавим агенту знание, с какой стороны от него расположен противник, а также находится агент на кромке поля или нет.

features 3
    def get_features(self,x,y):
        features=[]
        for i in self.ens:
          ex,ey=i.getxy()
          features.append(x-ex)
          features.append(y-ey)
        # if near wall x & y.
        if x==0:
            features.append(-1)
        elif x==self.n-1:
            features.append(1)
        else:
            features.append(0)
        if y==0:
            features.append(-1)
        elif y==self.n-1:
            features.append(1)
        else:
            features.append(0)
        return features


Такой набор переменных сразу значительно поднимает среднее количество баллов до 400–800. График обучения:

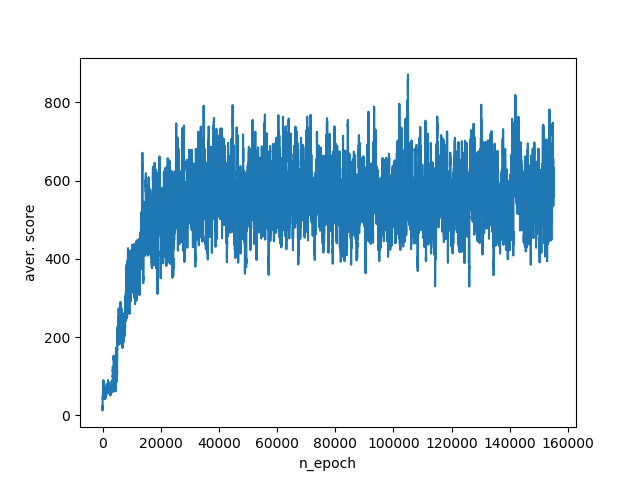
y_sbur_mfidtbow9uffihsqzh18.png

Наконец, отдадим алгоритму всю доступную информацию об окружении. А именно: абсолютные координаты агента и противника.

features 4
    def get_features(self,x,y):
        features=[]
        for i in self.ens:
          ex,ey=i.getxy()
          features.append(ex)
          features.append(ey)
        features.append(x)
        features.append(y)
        return features


Этот набор параметров дает возможность агенту набирать 800–1400 очков на тестовых симуляциях. График обучения:

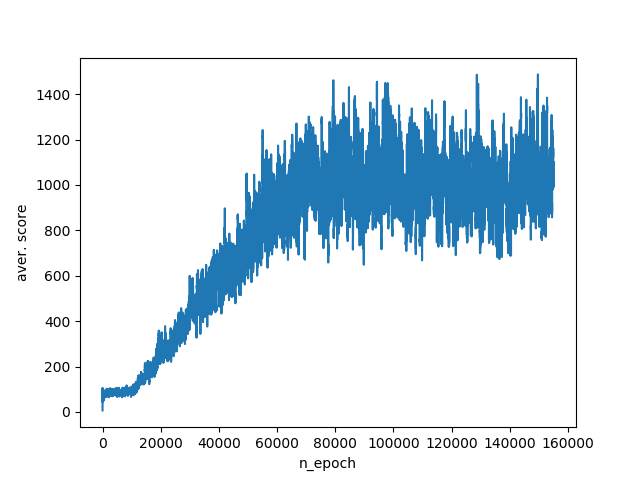
afjkx56af2so5g0gebbh0_z1syc.png

Итак, мы рассмотрели работу алгоритма q-learning. Покрутив параметры, которые отвечают за восприятие агентом окружения, наглядно убедились, как адекватная передача информации и учет всех аспектов при описании окружения влияет на результативность его действий. Однако у полного описания окружения есть обратная сторона. А именно взрывной рост пространства состояний при увеличении количества передаваемой агенту информации. Чтобы обойти эту проблему, были разработаны алгоритмы аппроксимирующие пространство состояний, например DQN алгоритм.

Полезные ссылки:

habrahabr.ru/post/274597
ai.berkeley.edu/reinforcement.html

Полный код программ:

1. Базовая модель окружения (из части 1)
import random
import time

class W:
    def __init__(self,n):
        self.n=n
        self.P=P(1,1,n) 
        self.ens=[EN(3,3,n),EN(4,4,n),EN(5,5,n)]
    def step(self):
        for i in self.ens:
            i.move()
        self.P.move()
    def pr(self):
        print('\n'*100)
        px,py=self.P.getxy()
        self.wmap=list([[0 for i in range(self.n)] for j in range(self.n)])
        self.wmap[py][px]=1
        for i in self.ens:
            ex,ey=i.getxy()
            self.wmap[ey][ex]=2
        for i in self.wmap:
            print(i)
    def play(self):
        px,py=self.P.getxy()
        bl=True
        for i in self.ens:
            ex,ey=i.getxy()
            bl=bl and (px,py)!=(ex,ey)
        iter=0
        while bl:
            time.sleep(1)
            wr.pr()
            self.step()
            px,py=self.P.getxy()
            bl=True
            for i in self.ens:
                ex,ey=i.getxy()
                bl=bl and (px,py)!=(ex,ey)
                print((px,py),(ex,ey))
            print('___')
            iter=iter+1
        print(iter)

class un:
    def __init__(self,x,y):
        self.x = x
        self.y = y
    def getxy(self):
        return self.x, self.y

class P(un):
    def __init__(self,x,y,n):
        self.n=n
        un.__init__(self,x,y)
    def strtg(self):
        return 0,0
    def move(self):
        dx,dy=self.strtg()
        a=self.x+dx
        b=self.y+dy
        expr=((0<=a


2. Модель окружения с обучением агента на 500+1500 симуляциях
import random
import time
from math import hypot,pi,cos,sin,sqrt,exp
import plot_epoch

class Q:
    def __init__(self):
        self.gamma=0.95
        self.alpha=0.05
        self.state={}

    def get_wp(self,plr):
        self.plr=plr

    def run_model(self,silent=1):
        self.plr.prev_state=self.plr.curr_state[:-2]+(self.plr.dx,self.plr.dy)
        self.plr.curr_state=tuple(self.plr.get_features(self.plr.x,self.plr.y))+(self.plr.dx,self.plr.dy)

        if not silent:
            print(self.plr.prev_state)
            print(self.plr.curr_state)

        r=self.plr.reward   

        if self.plr.prev_state not in self.state:
            self.state[self.plr.prev_state]=0
        
        nvec=[]
        for i in self.plr.actions:
            cstate=self.plr.curr_state[:-2]+(i[0],i[1])
            if cstate not in self.state:
                self.state[cstate]=0
            nvec.append(self.state[cstate])

        nvec=max(nvec)

        self.state[self.plr.prev_state]=self.state[self.plr.prev_state]+self.alpha*(
                                       -self.state[self.plr.prev_state]+r+self.gamma*nvec)

class un:
    def __init__(self,x,y):
        self.x = x
        self.y = y
        self.actions=[(0,0),(-1,-1),(0,-1),(1,-1),(-1,0),
                       (1,0),(-1,1),(0,1),(1,1)]
    def getxy(self):
        return self.x, self.y

class P(un):
    def __init__(self,x,y,n,ens,QM,wrld):
        self.wrld=wrld
        self.QM=QM
        self.ens=ens
        self.n=n
        self.dx=0
        self.dy=0
        self.eps=0.95
        self.prev_state=tuple(self.get_features(x,y))+(self.dx,self.dy)
        self.curr_state=tuple(self.get_features(x,y))+(self.dx,self.dy)
        un.__init__(self,x,y)

    def get_features(self,x,y):
        features=[]

        # for i in self.ens: #80-100
        #     ex,ey=i.getxy()
        #     dx=abs(x-ex)
        #     dy=abs(y-ey)
        #     l=hypot(dx,dy)
        #     features.append(l)
        # to_brdr=min(x,y,self.n-1-x,self.n-1-y)
        # features.append(to_brdr)
        
        for i in self.ens: #800-1400
          ex,ey=i.getxy()
          features.append(ex)
          features.append(ey)
        features.append(x)
        features.append(y)

        # for i in self.ens: #800-1400
        #   ex,ey=i.getxy()
        #   features.append(x-ex)
        #   features.append(y-ey)
        # features.append(self.n-1-x)
        # features.append(self.n-1-y)

        # for i in self.ens: #400-800
        #   ex,ey=i.getxy()
        #   features.append(x-ex)
        #   features.append(y-ey)
        # # if near wall x & y.
        # if x==0:
        #     features.append(-1)
        # elif x==self.n-1:
        #     features.append(1)
        # else:
        #     features.append(0)
        # if y==0:
        #     features.append(-1)
        # elif y==self.n-1:
        #     features.append(1)
        # else:
        #     features.append(0)

        # features=[]        #40-80

        return features

    def strtg(self):
        if random.random()


3. Модуль вывода графиков (plot_epoch.py).
import matplotlib.pyplot as plt

class epoch_graph:
    def __init__(self):
        self.it=0
        self.iter=[]
        self.number=[]
        self.iter_aver=[]

    def plt_append(self,iter):
        self.it=self.it+1
        self.iter.append(iter)
        self.number.append(self.it)
        if len(self.iter)>100:
            self.iter_aver.append(sum(self.iter[-100:])/100)
        else:
            self.iter_aver.append(sum(self.iter)/len(self.iter))

    def plt_virt_game(self,W,QModel):
        wr=W(5,QModel)
        wr.P.eps=0.0
        iter=wr.play(1,0)
        self.plt_append(iter)

    def plot_graph(self):
        plt.plot(self.number,self.iter_aver)
        plt.xlabel('n_epoch')
        plt.ylabel('aver. score')
        plt.show()

© Habrahabr.ru