[Из песочницы] Обнаружение столкновений и теорема о разделяющей оси04.07.2020 23:02

В наше время компьютеры представляют собой мощные вычислительные машины,
способные выполнять миллионы операций в секунду. И естественно не обойтись без симуляции реального или игрового мира. Одна из задач компьютерного моделирования и симуляции состоит в определении столкновения двух объектов, одно из решений которой реализуется теоремой о разделяющей оси.

krnzcmfdifg3rjsy-ess2yqnrtw.jpeg
Примечание. В статье будет приведен пример с 2 параллелепипедами (далее — кубы), но идея для других выпуклых объектов будет сохранена.
Примечание. Вся реализация будет выполнена в Unity.

Акт 0. Общая теория


Для начала нужно познакомиться с «теоремой о разделяющей гиперплоскости».Именно она будет лежать в основе алгоритма.

Теорема. Две выпуклые геометрии не пересекаются, тогда и только тогда, когда между ними существует гиперплоскость, которая их разделяет. Ось ортогональная разделяющей
гиперплоскости называется разделяющей осью, а проекции фигур на нее не пересекаются.

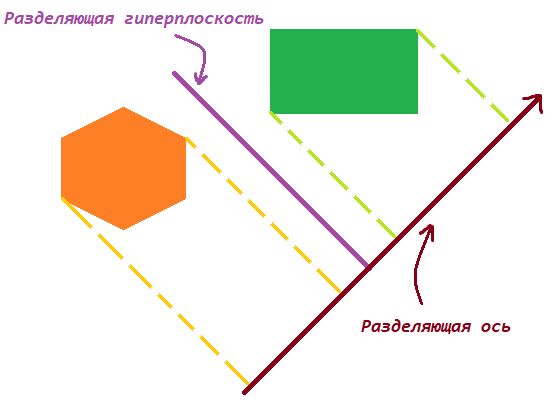
yzhwx5bdreqmndz_lln5qelnmx0.png
Разделяющая ось (двумерный случай)

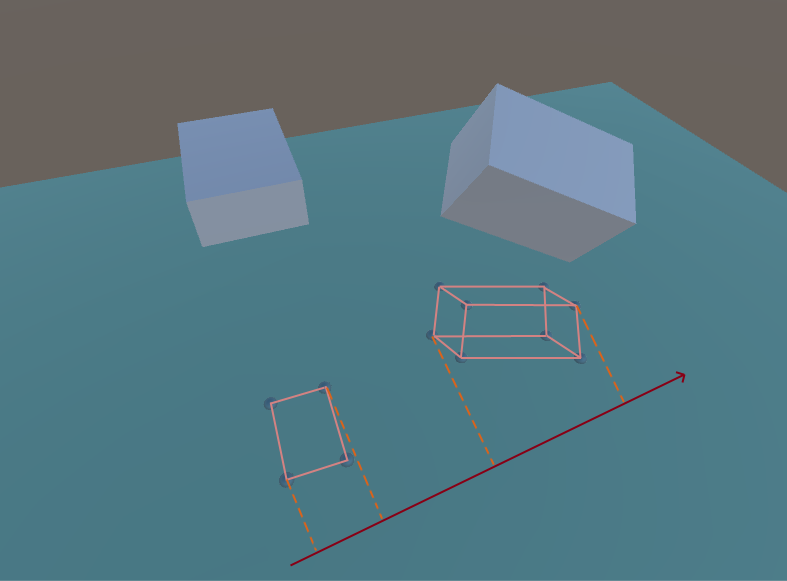
i79dnnhsjdbjbrdmu_6de37dpny.png
Разделяющая ось (трехмерный случай)
Можно заметить, что проекции на разделяющую ось не пересекаются.

Свойство. Потенциальная разделяющая ось будет находиться в следующих множествах:

  • Нормы плоскостей каждого куба (красные)
  • Векторное произведение ребер кубов $\{[\vec{x},\vec{y}] : x∈X, y∈Y\}$,


   где X — ребра первого куба (зеленые), а Y — второго (синие).

fgqpzo0hqbi_9s0fntio17pwrj0.png

Каждый куб мы можем описать следующими входными данными:

  • Координаты центра куба
  • Размеры куба (высота, ширина, глубина)
  • Кватернион куба


Создадим для этого дополнительный класс, экземпляры которого будут предоставлять информацию о кубе.

public class Box
{
    public Vector3 Center;
    public Vector3 Size;
    public Quaternion Quaternion;

    public Box(Vector3 center, Vector3 size, Quaternion quaternion)
    {
       this.Center = center;
       this.Size = size;
       this.Quaternion = quaternion;
    }
    // дополнительный конструктор, который
    // позволяет сгенерировать объект на основе GameObject
    public Box(GameObject obj)
    {
        Center = obj.transform.position;
        Size = obj.transform.lossyScale;
        Quaternion = obj.transform.rotation;
    }

}


Акт 1. Кватернионы


Как часто бывает, объект может вращаться в пространстве. Для того, чтобы найти координаты вершин, с учетом вращения куба, необходимо понять, что такое кватернион.

Кватернион — это гиперкомплексное число, которое определяет вращение объекта в пространстве.

$w+xi+yj+zk$


Мнимая часть (x, y, z) представляет вектор, который определяет направление вращения
Вещественная часть (w) определяет угол, на который будет совершено вращение.

Его основное отличие от всем привычных углов Эйлера в том, что нам достаточно иметь один вектор, который будет определять направление вращения, чем три линейно независимых вектора, которые вращают объект в 3 подпространствах.

Рекомендую две статьи, в которых подробно рассказывается о кватернионах:

Раз
Два

Теперь, когда у нас есть минимальные представления о кватернионах, давайте поймем, как вращать вектор, и опишем функцию вращение вектора кватернионом.

Формула вращения вектора

$\vec{v}' = q * \vec{v} * \overline{q}$


$\vec{v}'$ — искомый вектор
$\vec{v}$ — исходный вектор
$q$ — кватернион
$\overline{q}$ — обратный кватернион

Для начала, дадим понятие обратного кватерниона в ортонормированном базисе — это кватернион с противоположной по знаку мнимой частью.

$q = w+xi+yj+zk$
$\overline{q} = w-xi-yj-zk$

Посчитаем $\vec{v} * \overline{q}$

$ M = \vec{v}*\overline{q} = (0 + v_xi + v_yj + v_zk)(q_w - q_xi - q_yj - q_zk) = $
$=\color{red}{v_xq_wi} + \color{purple}{v_xq_x} - \color{blue}{v_xq_yk} + \color{green}{v_xq_zj} +$
$+\color{green}{v_yq_wj} + \color{blue}{v_yq_xk} + \color{purple}{v_yq_y} - \color{red}{v_yq_zi} +$
$+\color{blue}{v_zq_wk} - \color{green}{v_zq_xj} + \color{red}{v_zq_yi} + \color{purple}{v_zq_z}$

Теперь выпишем отдельные компоненты и из этого произведения соберем новый кватернион
$M = u_w+u_xi+u_yj+u_zk$
$u_w = \color{purple}{v_xq_x + v_yq_y + v_zq_z}$
$u_xi = \color{red}{(v_xq_w - v_yq_z + v_zq_y)i}$
$u_yj = \color{green}{(v_xq_z + v_yq_w - v_zq_x)j}$
$u_zk = \color{blue}{(-v_xq_y + v_yq_x + v_zq_w)k}$

Посчитаем оставшуюся часть, т.е. $ q*M $ и получим искомый вектор.

Примечание. Чтобы не загромождать вычисления, приведем только мнимую (векторную) часть этого произведения. Ведь именно она характеризует искомый вектор.

$\vec{v}' = q*M = (q_w + q_xi + q_yj + q_zk)(u_w + u_xi + u_yj + u_zk) =$
$= \color{red}{q_wu_xi} + \color{green}{q_wu_yj} + \color{blue}{q_wu_zk} + $
$ +\color{red}{q_xu_wi} + \color{blue}{q_xu_yk} - \color{green}{q_xu_zj} +$
$+\color{green}{q_yu_wj} - \color{blue}{q_yu_xk} + \color{red}{q_yu_zi} +$
$+\color{blue}{q_zu_wk} +\color{green}{q_zu_xj} -\color{red}{q_zu_yi}$

Соберем компоненты вектора

$v_x' = \color{red}{q_wu_x + q_xu_w + q_yu_z - q_zu_y}$
$v_y' = \color{green}{q_wu_y - q_xu_z + q_yu_w + q_zu_x}$
$v_z' = \color{blue}{q_wu_z + q_xu_y - q_yu_x + q_zu_w}$

$v' = (v_x', v_y', v_z')$
Таким образом необходимый вектор получен

Напишем код: 

private static Vector3 QuanRotation(Vector3 v,Quaternion q)
{
        float u0 = v.x * q.x + v.y * q.y + v.z * q.z;
        float u1 = v.x * q.w - v.y * q.z + v.z * q.y;
        float u2 = v.x * q.z + v.y * q.w - v.z * q.x;
        float u3 = -v.x * q.y + v.y * q.x + v.z * q.w;
        Quaternion M = new Quaternion(u1,u2,u3,u0);
        
        Vector3 resultVector;
        resultVector.x = q.w * M.x + q.x * M.w + q.y * M.z - q.z * M.y;  
        resultVector.y = q.w * M.y - q.x * M.z + q.y * M.w + q.z * M.x;
        resultVector.z = q.w * M.z + q.x * M.y - q.y * M.x + q.z * M.w;
        
        return resultVector;
}


Акт 2. Нахождение вершин куба


Зная как вращать вектор кватернионом, не составит труда найти все вершины куба.

Перейдем к функцию нахождении вершин куба. Определим базовые переменные.

private static Vector3[] GetPoint(Box box)
{
        //Тут будут храниться координаты вершин
        Vector3[] point = new Vector3[8];

        //получаем координаты
        //....

        return point;
}


Далее необходимо найти такую точку (опорную точку), от которой будет легче всего найти другие вершины.

Из центра покоординатно вычитаем половину размерности куба.Потом к опорной точке прибавляем по одной размерности куба.

//...
        //первые четыре вершины
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//таким же образом находим оставшееся точки
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);
//...


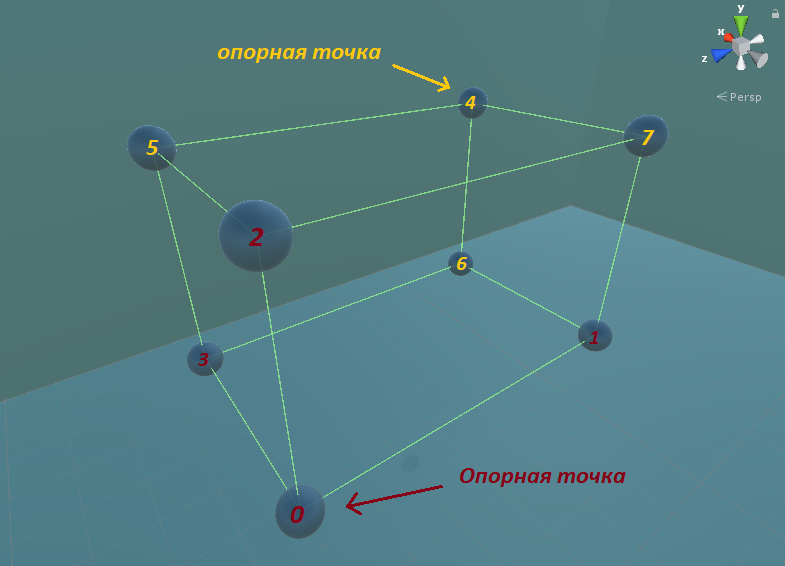
unfmfkxos3_df7226wultv5dabk.png
Можем видеть, как сформированы точки

После нахождения координат вершин, необходимо повернуть каждый вектор на соответствующий кватернион.

//...

        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//перенос центра в начало координат

            point[i] = QuanRotation(point[i], box.Quaternion);//поворот

            point[i] += box.Center;//обратный перенос
        }

//...


полный код получения вершин 
private static Vector3[] GetPoint(Box box)
{
        Vector3[] point = new Vector3[8];
        
        //получаем координаты вершин
        point[0] = box.Center - box.Size/2;
        point[1] = point[0] + new Vector3(box.Size.x , 0, 0);
        point[2] = point[0] + new Vector3(0, box.Size.y, 0);
        point[3] = point[0] + new Vector3(0, 0, box.Size.z);
		
	//таким же образом находим оставшееся точки
        point[4] = box.Center + box.Size / 2;
        point[5] = point[4] - new Vector3(box.Size.x, 0, 0);
        point[6] = point[4] - new Vector3(0, box.Size.y, 0);
        point[7] = point[4] - new Vector3(0, 0, box.Size.z);

        //поворачиваем вершины кватернионом
        for (int i = 0; i < 8; i++)
        {
            point[i] -= box.Center;//перенос центра в начало координат

            point[i] = QuanRotation(point[i], box.Quaternion);//поворот

            point[i] += box.Center;//обратный перенос
        }
        
        return point;
}


Перейдем к проекциям.

Акт 3. Поиск разделяющих осей


Следующим шагом необходимо найти множество осей, претендующих на разделяющую.
Вспомним, что ее можно найти в следующих множествах:

  • Нормали плоскостей каждого куба (красные)
  • Векторное произведение ребер кубов $\{[\vec{x},\vec{y}[ : x∈X, y∈Y\}$, где X — ребра первого куба (зеленые), а Y — второго (синие).


fgqpzo0hqbi_9s0fntio17pwrj0.png

Для того, чтобы получить необходимые оси, достаточно иметь четыре вершины куба, которые формируют ортогональную систему векторов. Эти вершины находятся в первых четырех ячейках массива точек, которые мы сформировали во втором акте.

76uluamafmv_aomhdxjh4hfup4k.png

Необходимо найти нормали плоскостей, порожденные векторами:


Для этого надо перебрать пары ребер куба так, чтобы каждая новая выборка образовывала плоскость, ортогональную всем предыдущим полученным плоскостям. Для меня невероятно тяжело было объяснить как это работает, поэтому я предоставил два варианта кода, которые помогут понять.

такой код позволяет получить эти вектора и найти нормали к плоскостям для двух кубов (понятный вариант) 
private static List GetAxis(Vector3[] a, Vector3[] b)
{
        //ребра
        Vector3 A;
        Vector3 B;

        //потенциальные разделяющие оси
        List Axis = new List();

        //нормали плоскостей первого куба
        A = a[1] - a[0];
        B = a[2] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = a[2] - a[0];
        B = a[3] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = a[1] - a[0];
        B = a[3] - a[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        

        //нормали второго куба
        A = b[1] - b[0];
        B = b[2] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = b[1] - b[0];
        B = b[3] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);
        
        A = b[2] - b[0];
        B = b[3] - b[0];
        Axis.Add(Vector3.Cross(A,B).normalized);

        //...
}


Но можно сделать проще: 

private static List GetAxis(Vector3[] a, Vector3[] b)
{
        //ребра
        Vector3 A;
        Vector3 B;

	//потенциальные разделяющие оси
        List Axis = new List();

	//нормали плоскостей первого куба
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//нормали второго куба
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //...
}


Еще мы должны найти все векторные произведения ребер кубов. Это можно организовать простым перебором: 

private static List GetAxis(Vector3[] a, Vector3[] b)
{
        //...
        //получение нормалей
        //... 

       //Теперь добавляем все векторные произведения
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}


Полный код 
private static List GetAxis(Vector3[] a, Vector3[] b)
{
	//ребра
        Vector3 A;
        Vector3 B;

	//потенциальные разделяющие оси
        List Axis = new List();

	//нормали плоскостей первого куба
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            B = a[(i+1)%3+1] - a[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }
	//нормали второго куба
        for (int i = 1; i < 4; i++)
        {
            A = b[i] - b[0];
            B = b[(i+1)%3+1] - b[0];
            Axis.Add(Vector3.Cross(A,B).normalized);
        }

        //Теперь добавляем все векторные произведения
        for (int i = 1; i < 4; i++)
        {
            A = a[i] - a[0];
            for (int j = 1; j < 4; j++)
            {
                B = b[j] - b[0];
                if (Vector3.Cross(A,B).magnitude != 0)
                {
                    Axis.Add(Vector3.Cross(A,B).normalized);
                }
            }
        }
        return Axis;
}


Акт 4. Проекции на оси


Мы подошли к самому главному моменту. Здесь мы должны найти проекции кубов на все потенциальные разделяющие оси. У теоремы есть одно важное следствие: если объекты пересекаются, то ось на которую величины пересечения проекции кубов минимальна — является направлением (нормалью) коллизии, а длинна отрезка пересечения — глубиной проникновения.

Но для начала напомним формулу скалярной проекции вектора v на единичный вектор a:

$proj_\left\langle \vec{a} \right\rangle \vec{v} = \frac{(\vec{v},\vec{a})}{| \vec{a} |}$

private static float ProjVector3(Vector3 v, Vector3 a)
{
        a = a.normalized;
        return Vector3.Dot(v, a) / a.magnitude;
        
}


Теперь опишем функцию, которая будет определять пересечение проекций на оси-кандидаты.

На вход подаем вершины двух кубов, и список потенциальных разделяющих осей: 

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
           //в этом цикле проверяем каждую ось
           //будем определять пересечение проекций на разделяющие оси из списка кандидатов
        }
        //Если мы в цикле не нашли разделяющие оси, то кубы пересекаются, и нам нужно 
        //определить глубину и нормаль пересечения.
}


Проекция на ось задается двумя точками, которые имеют максимальные и минимальные значения на самой оси:

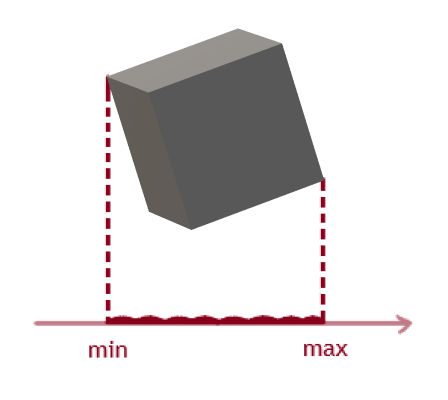
62gozr8cioxhnpo19t38zy7f1my.png

Далее создаем функцию, которая возвращает проекционные точки каждого куба. Она принимает два возвращаемых параметра, массив вершин и потенциальную разделяющую ось.

private static void ProjAxis(out float min, out float max, Vector3[] points, Vector3 Axis)
{
        max = ProjVector3(points[0], Axis);
        min = ProjVector3(points[0], Axis);
        for (int i = 1; i < points.Length; i++)
        {
            float tmp = ProjVector3(points[i], Axis);
            if (tmp > max)
            {
                max = tmp;
            }

            if (tmp < min)
            {
                min= tmp;
            }
        }
}


Итого, применив данную функцию (ProjAxis), получим проекционные точки каждого куба.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List Axis)
{
        for (int j = 0; j < Axis.Count; j++)
        {
            //проекции куба a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //проекции куба b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);
            
            //...
        }
        //...
}


Далее, на основе проекционных вершин определяем пересечение проекций:

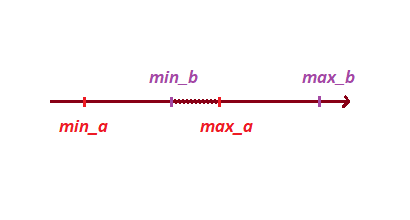
ogbaetjzgs0e5b8gd7dv1ldmf5s.png

Для этого давайте поместим наши точки в массив и отсортируем его, такой способ поможет нам определить не только пересечение, но и глубину пересечения.

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);


Заметим следующее свойство:

1) Если отрезки не пересекаются, то сумма отрезков будет меньше, чем отрезок сформированными крайними точками:

j4cv66psvb7fdjlyudpcb9z8aeq.png

2) Если отрезки пересекаются, то сумма отрезков будет больше, чем отрезок сформированными крайними точками:

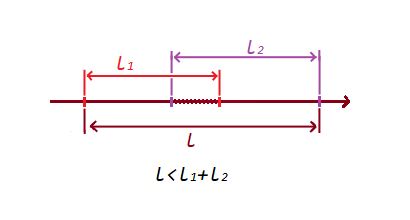
zz-btwa_42iu9zxd733dmpvmrye.png

Вот таким простым условием мы проверили пересечение и непересечение отрезков.

Если пересечения нет, то глубина пересечения будет равна нулю: 

            //...
            //Сумма отрезков
            float sum = (max_b - min_b) + (max_a - min_a);
            //Длина крайних точек
            float len = Math.Abs(p[3] - p[0]);
            
            if (sum <= len)
            {
                //разделяющая ось существует
                // объекты непересекаются
                return Vector3.zero;
            }
            //Предполагаем, что кубы пересекаются и рассматриваем текущую ось далее
            //....


Таким образом, нам достаточно иметь хоть один вектор, на котором проекции кубов не пересекаются, тогда и сами кубы не пересекаются. Поэтому, когда мы найдем разделяющую ось, мы сможем не проверять оставшееся вектора, и завершить работу алгоритма.

В случае пересечения кубов, все немного интереснее: проекции кубов на все вектора будет пересекаться, и мы должны определить вектор с минимальным пересечением.

Создадим этот вектор перед циклом, и будем хранить в нем вектор с минимальной длинной. Тем самым в конце работы цикла получим искомый вектор.

private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
                //...
        }
        //в случае, когда нашелся вектор с минимальным пересечением, возвращаем его
        return norm;
{


И каждый раз, когда мы находим ось, на которой проекции пересекаются, проверяем является ли она минимальной по длине среди всех. такую ось умножаем на длину пересечения, и результатом будет искомая нормаль (направление) пересечения кубов.

Так же я добавил определение ориентации нормали по отношению первого куба.

//...
if (sum <= len)
{
   //разделяющая ось существует
   // объекты не пересекаются
   return new Vector3(0,0,0);
}
//Предполагаем, что кубы пересекаются и рассматриваем текущий вектор далее

//пересечение проекций - это расстояние между 2 и 1 элементом в нашем массиве
//(см. рисунок на котором изображен случай пересечения отрезков)
float dl = Math.Abs(points[2] - points[1]);
if (dl < norm.magnitude)
{
   norm = Axis[j] * dl;
   //ориентация нормали
   if(points[0] != min_a)
   norm = -norm;
}
//...


Весь код 
private static Vector3 IntersectionOfProj(Vector3[] a, Vector3[] b, List Axis)
{
        Vector3 norm = new Vector3(10000,10000,10000);
        for (int j = 0; j < Axis.Count; j++)
        {
            //проекции куба a
            float max_a;
            float min_a;
            ProjAxis(out min_a,out max_a,a,Axis[j]);

            //проекции куба b
            float max_b;
            float min_b;
            ProjAxis(out min_b,out max_b,b,Axis[j]);

            float[] points = {min_a, max_a, min_b, max_b};
            Array.Sort(points);

            float sum = (max_b - min_b) + (max_a - min_a);
            float len = Math.Abs(points[3] - points[0]);
            
            if (sum <= len)
            {
                //разделяющая ось существует
                // объекты не пересекаются
                return new Vector3(0,0,0);
            }
            float dl = Math.Abs(points[2] - points[1]);
            if (dl < norm.magnitude)
            {
                norm = Axis[j] * dl;

                //ориентация нормы
                if(points[0] != min_a)
                    norm = -norm;
            }

        }
        return norm;
}


Заключение


Проект с реализацией и примером загружен на GitHub, и ознакомиться можно с ним здесь.

Моей целью было поделиться своим опытом в решение задач связанных с определением пересечений двух выпуклых объектов. А так же доступно и понятно рассказать о данной теореме.

© Habrahabr.ru