[Из песочницы] Моделирование мира и динамические системы
В статье рассказывается об одной статистической закономерности, объяснение которой приведет к интересным задачам как прикладного, так и чисто теоретического характера.
(Первые цифры площадей стран, записанных в десятичной записи)
Начнем с рассмотрения одного, на первый взгляд бессмысленного, статистического показателя. Запишем численности населения всех стран мира в десятичной записи и посмотрим, как часто каждая цифра от 1 до 9 является первой цифрой одного из этих чисел.
Получится такой результат (численности населения брались из Википедии):
1
2
3
4
5
6
7
8
9
0.265
0.176
0.134
0.093
0.089
0.081
0.044
0.069
0.049
Уже видна странная монотонность. Для пущей наглядности построим график: 
Получился удивительный результат. Десятичная система счисления — всего лишь инструмент, она не является какой-то выделенной или фундаментальной, так что посчитанное распределение должно бы быть бессмысленным и не имеющим никаких видимых закономерностей, однако мы видим явную монотонность.
Пока что это вполне можно счесть случайностью, не имеющей никаких фундаментальных причин. Какие-то 9 чисел вдруг оказались вдруг оказались как-то упорядочены (и то не совсем, частота семерки меньше частот восьмерки и девятки) — мало ли.
Тогда давайте проделаем аналогичную процедуру с другим географическим показателем — площадью стран мира.
1
2
3
4
5
6
7
8
9
0.298
0.183
0.109
0.115
0.068
0.075
0.063
0.041
0.048
Тоже построим график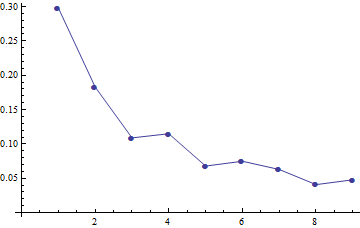
Монотонность все же не идеальная, но явно заметная.
Неужели это какая-то общая закономерность? Давайте посмотрим на площади американских штатов
Что же, такой неприличной монотонности уже не наблюдается. Это наводит на мысль о происхождении закономерности. Площади и популяции стран мира активно менялись по ходу истории, площади же штатов однажды были искусственно определены и естественному изменению не подвергались.(Интересно заметить, что ища контрпример, я перебрал объем потребления пива, объем производства томатов и размер железнодорожных сетей — все они показали некоторую монотонность, скорее всего это связано с тем, что эти величины заметно коррелируют с численностью населения и площадью). Перейдем наконец к объяснению.
Математическое объяснениеРассмотрим аналогичный показатель — частоты первых цифр в десятичной записи для геометрической прогрессии — 1,2,4,…,2n. Взяв n=1000, получим:1
2
3
4
5
6
7
8
9
0.301
0.177
0.124
0.097
0.080
0.067
0.057
0.052
0.044
Видна похожая закономерность — монотонность и единица встречается в несколько раз чаще девятки. У этого факта есть строгое математическое доказательство. Для данной статьи оно не очень важно, хотя и является интересным само по себе.Доказательство
Доказательство теоремыЗначит, в пределе получим такой результат:1
2
3
4
5
6
7
8
9
lg 2
lg 3/2
lg 4/3
lg 5/4
lg 6/5
lg 7/6
lg 8/7
lg 9/8
lg 10/9
0.301
0.176
0.125
0.097
0.079
0.067
0.058
0.051
0.046
Самим по себе удивительным является тот факт, что эти частоты не зависят от выбора знаменателя прогрессии.
Идея следующего рассуждения, насколько мне известно, принадлежит великому математику В.И. Арнольду.Значит, мы установили, что первые цифры чисел из геометрической прогрессии подчиняются похожему распределению. Как же теперь можно объяснить эту связь? Арнольд предположил, что дело здесь в эргодичности этой системы (наглядная заметка об этом понятии), то есть в том, что пространственная средняя величина (здесь это как раз та статистика, которую мы подсчитали) равна временной средней величине в одной точке пространства (то есть аналогичная статистика, взятая для значений популяции одной страны в длительный промежуток времени). Под пространством здесь понимается фазовое пространство — множество стран. В этом случае это можно интерпретировать так: все страны мира в данный момент можно рассматривать как этапы развития одной и той же страны на протяжении истории, это соответствие весьма неточное, набор популяций стран мира в данный момент не совпадает с набором популяций одной страны за некоторое время, однако же средние величины, которые мы исследуем, совпадают.
Таким образом, задача свелась к исследованию динамики популяции одной страны. Ее уже можно приблизить геометрической прогрессией. Локально, конечно, это приближение весьма неточно, но первая цифра числа — параметр, который мало чувствителен к небольшим изменениям числа, так что если на большом отрезке времени динамика популяции похожа на экспоненту, распределение частот первых цифр будет похоже на полученное теоретическим путем.
Вот графики, иллюстрирующие это явление
Ну что же, замеченный эффект для населений объяснить удалось. Как же быть с площадями?
Площади Их уже ни в каком приближении нельзя назвать растущими экспоненциально. Здесь можно предложить такую математическую модель: мир начинается с некоторого количества одинаковых по площади стран. В каждую единицу времени равновероятно происходит одно из двух событий: случайно выбранная страна делится на две одинаковой площади или две случайно выбранные страны одинаковой площади объединяются в одну. Эта модель допускает строгое математическое исследование, но оно уже совсем далеко от темы статьи, так что я не буду его приводить. Как бы то ни было, такая модель приводит к похожему распределению частот.Однако, она выглядит не очень похожей на реальность. Да, в мире страны иногда объединяются, иногда делятся пополам, но соотношения площадей далеко не фиксированы и объединяются, как правило, только страны, имеющие общую границу. Учитывая все эти факторы, можно усовершенствовать модель, но для математики она станет уже неподъемной (это мое личное мнение, возможно, кому-то удалось получить достойные результаты в этом направлении).
Здесь на помощь приходит компьютерное моделирование. Я выбрал такую модель: мир — прямоугольник, страны — прямоугольники, стороны которых параллельны сторонам мира. За единицу времени с вероятностью p две страны, имеющие общую сторону сливаются в одну, с вероятностью (1-p) одна страна делится на две разрезом по прямой.
Для реализации я выбрал первое что попалось под руку, так что извините, если мой выбор покажется странным. Это Python 2.7 с использованием модуля pygame.
Код (писался исключительно на результат, так что весьма непричесан) import pygame import random import time
cell_size = 10 WIN_WIDTH = 850 WIN_HEIGHT = 850 BACKGROUND_COLOR = »#D3D3D3» DISPLAY = (WIN_WIDTH, WIN_HEIGHT) p = 0.3
class Country (object):
def __init__(self, x, y, dx, dy): self.x = x self.y = y self.dx = dx self.dy = dy self.color = (random.choice (range (256)), random.choice (range (256)), random.choice (range (256)))
def get_neighbs (self, countries): self.neighbors = [] for i in range (len (countries)): c = countries[i] if c.x == self.x and c.dx == self.dx and (c.y + c.dy == self.y or c.y == self.y + self.dy): self.neighbors.append (i) if c.y == self.y and c.dy == self.dy and (c.x + c.dx == self.x or c.x == self.x + self.dx): self.neighbors.append (i)
def __repr__(self): return str ((self.x, self.y, self.dx, self.dy, self.neighbors))
__str__ = __repr__
def draw (self, screen): self.image = pygame.Rect (self.x, self.y, self.dx, self.dy) pygame.draw.rect (screen, self.color, self.image)
def area (self): return self.dx * self.dy
def world_init (): countries = [Country (50, 50, 250, 250), Country (300, 50, 250, 250), Country (550, 50, 250, 250), Country (50, 300, 250, 250), Country (300, 300, 250, 250), Country (550, 300, 250, 250), Country (50, 550, 250, 250), Country (300, 550, 250, 250), Country (550, 550, 250, 250)] for c in countries: c.get_neighbs (countries) return countries
def merge (countries, i, j): »«i < j""" if countries[i].x < countries[j].x: new_country = Country(countries[i].x, countries[i].y, countries[i].dx + countries[j].dx, countries[i].dy) if countries[i].y < countries[j].y: new_country = Country(countries[i].x, countries[i].y, countries[i].dx, countries[i].dy + countries[j].dy) if countries[i].x > countries[j].x: new_country = Country (countries[j].x, countries[j].y, countries[j].dx + countries[i].dx, countries[j].dy) if countries[i].y > countries[j].y: new_country = Country (countries[j].x, countries[j].y, countries[j].dx, countries[j].dy + countries[i].dy) del countries[i] del countries[j — 1] countries.append (new_country) for c in countries: c.get_neighbs (countries)
def divide (countries, i, midx=0, midy=0): print countries[i].area () if midy == 0: new1 = Country (countries[i].x, countries[i].y, midx, countries[i].dy) new2 = Country (countries[i].x + midx, countries[i].y, countries[i].dx — midx, countries[i].dy) del countries[i] countries.append (new1) countries.append (new2) for c in countries: c.get_neighbs (countries) if midx == 0: new1 = Country (countries[i].x, countries[i].y, countries[i].dx, midy) new2 = Country (countries[i].x, countries[i].y + midy, countries[i].dx, countries[i].dy — midy) del countries[i] countries.append (new1) countries.append (new2) for c in countries: c.get_neighbs (countries)
def world_draw (countries, screen): for c in countries: c.draw (screen)
def random_action (countries): rand = (random.uniform (0, 1) < p) if rand: i = random.choice(range(len(countries))) if countries[i].neighbors: j = random.choice(countries[i].neighbors) merge(countries, i, j) else: i = random.choice(range(len(countries))) xaxis = random.choice([True, False]) if xaxis: try: mid = random.choice(range(cell_size, countries[i].dx, cell_size)) except IndexError: return 0 divide(countries, i, midx=mid) else: try: mid = random.choice(range(cell_size, countries[i].dy, cell_size)) except IndexError: return 0 divide(countries, i, midy=mid)
def get_stat (countries): digits = [int (str (c.area ())[0]) for c in countries]
result = {0:0.0, 1:0.0, 2:0.0, 3:0.0, 4:0.0, 5:0.0, 6:0.0, 7:0.0, 8:0.0, 9:0.0}
for d in digits: result[d] += 1
for d in range (1, 10): result[d] = round (result[d] / len (digits), 3)
return result
def main (): pygame.init () screen = pygame.display.set_mode (DISPLAY) pygame.display.set_caption («World History») bg = pygame.Surface ((WIN_WIDTH, WIN_HEIGHT)) bg.fill (pygame.Color (BACKGROUND_COLOR)) countries = world_init () waiting = True while waiting: events = pygame.event.get () for event in events: if event.type == pygame.KEYDOWN: if event.key == pygame.K_SPACE: waiting = False
for i in range (1000): for e in pygame.event.get (): if e.type == pygame.QUIT: raise SystemExit, «QUIT» world_draw (countries, screen) pygame.display.update () random_action (countries) time.sleep (0.07) print get_stat (countries)
main ()
Вот видео работы программы (здесь 1000 итераций):[embedded content]На 1000 итерациях статистика еще не совсем совпадает с теоретической, а на 10000 уже близко:
1 2 3 4 5 6 7 8 9 0.435 0.226 0.106 0.085 0.045 0.038 0.020 0.029 0.015 Эти данные получены при p=0.3. Экспериментируя с различными значениями p и начальной конфигурацией мира, будем везде при достаточно большом числе итераций получать похожие результаты, так что, видимо, рассматриваемое условие является общим для всех моделей такого типаИтак, такой, на первый взгляд бессмысленный, экспериментальный факт, привел нас к таким глубоким разделам математики как теория чисел и теория динамических систем
P.S. Идеи математической части данной статьи я почерпнул из какой-то научно-популярной статьи В.И. Арнольда, которую я когда-то читал, но к сожалению сейчас мне не удалось найти ее.
