[Из песочницы] МЭМС акселерометры, магнитометры и углы ориентации

При разработке устройств, в которых необходимо оценивать углы ориентации, может встать вопрос — какой МЭМС датчик выбрать. Производители датчиков приводят множество параметров, из которых нам требуется получить полезную информацию о качестве датчика.
Чтобы понять, на какие точности углов мы можем рассчитывать, нужно приложить некоторое количество усилий.
TL; DR: Описан небольшой скрипт для Octave/MATLAB, позволяющий оценить ошибки расчёта углов ориентации по измерениям МЭМС акселерометров и магнитометров. На входе скрипта — параметры датчиков из даташитов (и/или погрешности калибровки). Статья может быть полезна тем, кто начинает использовать инерциальные датчики в своих устройствах. Небольшой ликбез по датчикам прилагается. Ссылка на гитхаб тоже.
Сходу примем такие условия:
- Мы хотим оценить углы ориентации неподвижного устройства. Почему?
Ориентацию подвижного устройства просто по формулам не посчитать, нужно использовать хитрые алгоритмы.
- Для оценки углов мы будем использовать измерения МЭМС акселерометров и магнитометров.
1. Краткий ликбез
Углы ориентации
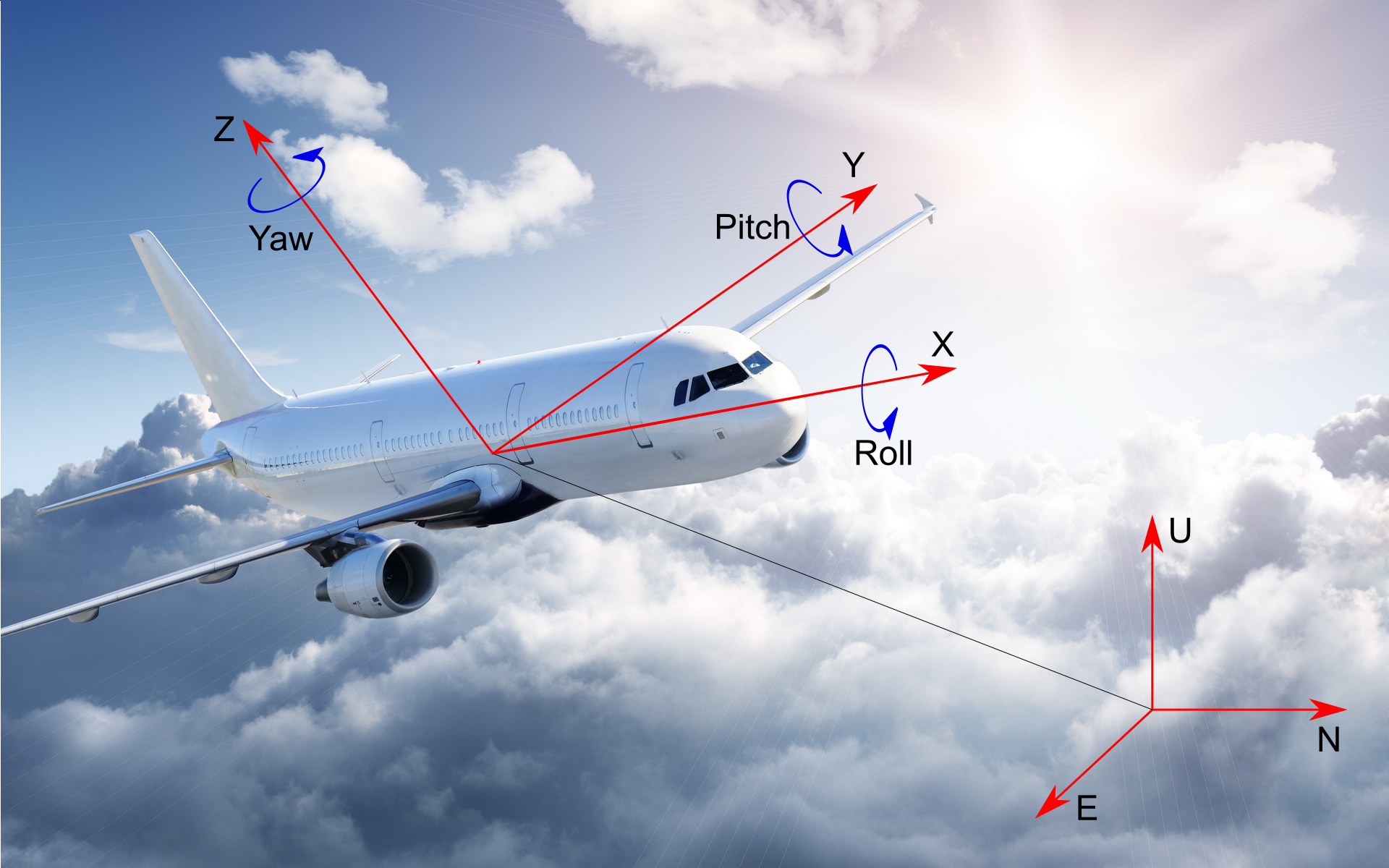
Будем понимать под углами ориентации объекта углы Эйлера — крен (roll), тангаж (pitch), рыскание (yaw), связывающие собственную систему координат XYZ объекта и локальную систему координат восток-север-верх (ENU — East North Up). Углы roll, pitch, yaw обозначают поворот, который нужно совершить осям XYZ чтобы перейти в оси ENU. Соответственно, нулевые углы означают, что ось X объекта смотрит на восток, ось Y объекта смотрит на север, ось Z — вверх.
Порядок поворота осей — начиная с последнего угла: сначала на yaw (вокруг оси Z), потом на pitch (вокруг оси Y), потом на roll (вокруг оси X).
Акселерометр
Это датчик, измеряющий проекцию кажущегося ускорения на ось чувствительности. Кажущегося — потому что измеряет и силу тяжести тоже, даже в то время как акселерометр неподвижен. Проще всего представить акселерометр как грузик на пружинке, его выдаваемые измерения пропорциональны степени растяжения пружины. Если акселерометр покоится — пружина растянута лишь силой тяжести. Если ускоряется — то будет сумма сил: инерции грузика $inline$\left (F=m\overrightarrow{a}\right)$inline$ и силы тяжести $inline$\left (F_{g}=m\overrightarrow{g}\right)$inline$
Примем следующую модель измерений триады ортогональных (взаимно перпендикулярных) акселерометров:
$$display$$a_{XYZ}= m_{a} \cdot A_{XYZ}+b_{a}+n_{a},$$display$$
где $inline$a_{XYZ}$inline$ — измеряемое ускорение в ССК (собственной системе координат) XYZ, $inline$m_{a}$inline$ — матрица перекоса осей и масштабных коэффициентов акселерометра, $inline$A_{XYZ}$inline$ — вектор истинного ускорения в ССК XYZ, $inline$b_{a}$inline$ — вектор смещения нуля акселерометра, $inline$n_{a}$inline$ — шум измерений.
Матрица перекоса осей и масштабных коэффициентов выглядит следующим образом:
$$display$$m_{a}=\begin{bmatrix}1+m_{a,1,1} & m_{a,1,2} & m_{a,1,3}\\ m_{a,2,1}& 1+m_{a,2,2} & m_{a,2,3}\\ m_{a,3,1} & m_{a,3,2} & 1+m_{a,3,3} \end{bmatrix},$$display$$
где элементы, расположенные по главной диагонали ($inline$ 1+m_{a,1,1}, 1+m_{a,2,2}, 1+m_{a,3,3}$inline$) — это масштабные коэффициенты и их погрешности по трём осям акселерометра, а остальные элементы матрицы — перекосы осей акселерометра.
Акселерометр MPU-9250
- Смещение нуля акселерометра — Zero-G Initial Calibration Tolerance ($inline$\pm60mg$inline$ для компонент $inline$X, Y$inline$, $inline$\pm80mg$inline$ для компоненты $inline$Z$inline$) — для расчётов переводим в единицы $inline$g$inline$ домножив на $inline$10^{-3};$inline$
- Погрешность масштабного коэффициента — Initial Tolerance ($inline$\pm3\%$inline$) — выражается в процентах. Для расчётов надо перевести в разы, домножив на $inline$10^{-2};$inline$
- Перекосы осей — Cross Axis Sensitivity ($inline$\pm2\%$inline$) — также умножаем на $inline$10^{-2};$inline$
- Спектральная плотность мощности шума акселерометра — Noise Power Spectral Density $inline$\left (300\frac{\mu g}{\sqrt{Hz}} \right)$inline$ — переводим числитель в $inline$g$inline$ домножая все на $inline$10^{-6};$inline$
- Полоса пропускания — Low Pass Filter Response $inline$\left (5–260 Hz\right)$inline$ — приведены границы, в пределах которых её можно изменять. Установим максимальную полосу. Все равно ошибки будут определяться не шумами;
Зная спектральную плотность мощности шума и полосу пропускания датчика можно рассчитать СКО шума на выходе датчика:
$$display$$\sigma _{noise}=G_{0}\cdot\sqrt{\Pi_{noise}};$$display$$
Акселерометр ADIS16488A:
- Смещение нуля — Bias Repeatability ($inline$\pm 16mg$inline$) — переводим в $inline$g$inline$ домножая на $inline$10^{-3};$inline$
- Погрешность масштабного коэффициента — (Sensitivity) Repeatability ($inline$\pm 0.5\%$inline$) — переводим из процентов в разы;
- Перекосы осей — Misalignment Axis to frame ($inline$\pm1^{\circ}$inline$) — в градусах, переводим в разы (радианы, поскольку величины малые);
- Спектральная плотность мощности шума — Noise Density $inline$\left (0.063\frac{mg}{\sqrt{Hz}}rms \right)$inline$ — переводим числитель в $inline$g;$inline$
- Полоса пропускания — $inline$\left (3dB Bandwidth\right)$inline$ — выберем такой же, как у MPU-9250;
Магнитометр
Датчик, который измеряет проекцию индукции магнитного поля на ось чувствительности. Магнитометру свойственны искажения hard-iron и soft-iron. Hard-iron искажение — это аддитивный эффект, когда к измеряемому полю добавляется постоянная составляющая. Причиной может быть, например, действие постоянного магнита или собственное смещение нуля датчика. Искажение soft-iron — мультипликативный эффект, отражающий изменение направления и/или ослабление вектора магнитной индукции. Этот эффект может быть вызван наличием металлического предмета в непосредственной близости от магнитометра или же собственными искажениями датчика — погрешностью масштабного коэффициента или перекосом его оси чувствительности.
Примем модель измерений триады магнитометров:
$$display$$m_{XYZ}=S_{m}\cdot M_{XYZ}+b_{m}+n_{m},$$display$$
где $inline$m_{XYZ}$inline$ — измерения магнитометра в ССК XYZ, $inline$S_{m}$inline$ — диагональная матрица перекоса осей и масштабных коэффициентов (которая описывает эффект soft–iron), $inline$M_{XYZ}$inline$ — вектор истинной магнитной индукции в ССК, $inline$b_{m}$inline$ — смещение нулей магнитометра (описывает эффект hard–iron), $inline$n_{m}$inline$ — шум измерений.
Матрица перекоса осей и масштабных коэффициентов магнитометра:
$$display$$S_{m}=\begin{bmatrix}1+S_{m,1,1} & S_{m,1,2} &S_{m,1,3}\\ S_{m,2,1}& 1+S_{m,2,2} & S_{m,2,3}\\ S_{m,3,1} & S_{m,3,2}&1+ S_{m,3,3} \end{bmatrix},$$display$$
элементы, расположенные на главной диагонали ($inline$S_{m,1,1}, S_{m,2,2}, S_{m,3,3}$inline$) — масштабные коэффициенты и их погрешности по трём осям магнитометра, остальные элементы матрицы — перекосы осей магнитометра. Все элементы матрицы также учитывают эффект soft-iron.
Магнитометр MPU-9250
В даташите нужных нам параметров нет, поэтому предположим, что магнитометр откалиброван и возьмем следующие числа:
- смещение нуля — $inline$(1\mu T);$inline$
- погрешность масштабных коэффициентов — $inline$(5\%);$inline$
- перекосы осей — предположим, что они такие же, как у акселерометров — $inline$(\pm2\%);$inline$
- шум на выходе — $inline$(0.6\mu T);$inline$
Магнитометр ADIS16488A
- Смещение нуля — Initial Bias Error $inline$\left (\pm15 mgauss = 1.5 \mu T \right)$inline$ — будем считать, что мы его откалибровали до $inline$(0.5 \mu T)$inline$;
- Погрешность масштабного коэффициента — Initial Sensitivity Tolerance $inline$\left (2\% \right);$inline$
- Перекосы осей — Misalignment Axis to axis $inline$\left (0.35^{\circ} \right)$inline$ — в градусах, переводим в разы (радианы, так как величина маленькая);
- Спектральная плотность мощности шума — Noise Density $inline$\left (0.042\frac{mgauss}{\sqrt{Hz}} \right)$inline$ — переводим в $inline$\left (\frac{Tesla}{\sqrt{Hz}} \right);$inline$
- Полоса пропускания — возьмем для модели значение $inline$260 Hz;$inline$
Расчет углов ориентации
Благодаря наличию на Земле силы тяжести, акселерометры «чувствуют» направление вниз. Их измерения используются для расчета углов крена и тангажа. Формулы для расчёта можно найти тут. Третий — угол рыскания (а в данном случае — магнитного азимута), может быть определен благодаря наличию у Земли магнитного поля. Вектор индукции магнитного поля измеряется магнитометрами и их измерения участвуют в расчете угла рыскания. Нужно отметить, что в расчёте магнитного азимута используются измерения магнитометра, пересчитанные в плоскость. Здесь можно найти формулу для расчёта магнитного азимута.
$$display$$roll=atan\left (\frac{a_{Y}}{a_{Z}} \right),$$display$$
$$display$$pitch=atan\left (\frac{-a_{X}}{\sqrt{a_{Y}^{2}+a_{Z}^{2}}} \right),$$display$$
$$display$$yaw=atan2\left (\frac{m_{E}}{m_{N}} \right),$$display$$
где $inline$atan2$inline$ — функция полного арктангенса, $inline$a_{X}$inline$, $inline$a_{Y}$inline$, $inline$a_{Z}$inline$ — измерения акселерометра по трём осям в ССК, $inline$m_{E}$inline$, $inline$m_{N}$inline$ — измерения магнитометра по осям X', Y' (измерения магнитометров пересчитаны в плоскость).
2. Ошибки оценивания углов ориентации
Описание алгоритма

- Сформируем массивы случайных углов Эйлера roll, pitch, yaw. Они будут задавать наборы вариантов истинной ориентации объекта в модели.Зачем много углов?
Потому что ошибки зависят от значения углов ориентации, и если мы хотим получить представление об их величине во всем диапазоне изменения — то это самый простой способ.
- Из случайных углов roll, pitch, yaw формируется матрица преобразования из ССК XYZ в ЛСК ENU:
$$display$$C_{XYZ}^{ENU}=\begin{vmatrix} cy\cdot cp &-cr\cdot sy+sr\cdot cy\cdot sp &sr\cdot sy+cr\cdot cy\cdot sp \\ sy\cdot cp &cr\cdot cy+sr\cdot sy\cdot sp & -sr\cdot cy+cr\cdot sy\cdot sp \\ -sp &sr\cdot cp &cr\cdot cp \end{vmatrix},$$display$$
где $inline$cr=\cos (roll)$inline$, $inline$sr=\sin (roll)$inline$, $inline$cp=\cos (pitch)$inline$, $inline$sp=\sin (pitch)$inline$, $inline$cy=\cos (yaw)$inline$, $inline$sy=\sin (yaw)$inline$. - Используя данную матрицу можно получить выражение для истинных ускорений в ССК:
$$display$$A_{XYZ}=\left (C_{XYZ}^{ENU} \right)^{T}\cdot \begin{vmatrix} 0\\ 0\\ -1\\ \end{vmatrix},$$display$$
$inline$\begin{vmatrix} 0\\ 0\\ -1\\ \end{vmatrix}$inline$ — вектор, определяющий направление гравитационного ускорения, выраженный в единицах g, $inline${(C_{XYZ}^{ENU})}^{T}$inline$ — матрица преобразования координат из ЛСК в ССК (обратная матрице преобразования из ССК в ЛСК). - Применяем модель измерения акселерометра:
$$display$$a_{XYZ}=\left (I+m_{a} \right)\cdot A_{XYZ}+b_{a}+n_{a},$$display$$
- По измерениям акселерометра рассчитываются новые углы крена и тангажа (оценки) по формулам:
$$display$$roll'=atan \left (\frac{a_{Y}}{a_{Z}} \right),$$display$$
$$display$$pitch'=atan\left (\frac{-a_{X}}{\sqrt{a_{Y}^{2}+a_{Z}^{2}}} \right).$$display$$
- Также необходимо сформировать матрицу пересчета в «горизонт» из этих углов, для этого воспользуемся функцией rpy2mat:
$$display$$C_{XYZ}^{XYZ'}=rpy2mat\left (\begin{bmatrix} roll'\\ pitch'\\ 0 \end{bmatrix}^{T} \right),$$display$$
где углы roll' и pitch' — это углы, рассчитанные по измерениям акселерометра, а третий угол — нулевой. - Возьмем вектор истинных магнитных плотностей в ЛСК ENU и пересчитаем его в ССК XYZ:
$$display$$M_{XYZ}= {(C_{XYZ}^{ENU})}^{T}\cdot M_{ENU}.$$display$$
- Применяем модель измерений магнитометра:
$$display$$m_{XYZ}=S_{m}\cdot M_{XYZ}+b_{m}+n_{m}.$$display$$
- Осталось пересчитать измерения магнитометра из ССК в «горизонт»:
$$display$$m_{XYZ'}=C_{XYZ}^{XYZ'}\cdot m_{XYZ}.$$display$$
- По «горизонтированным» измерениям магнитометра расcчитывается угол магнитного азимута:
$$display$$yaw'=atan2\left (\frac{m_{Y'}}{m_{X'}} \right).$$display$$
- Ошибки оценивания углов ориентации рассчитываются как разность между истинными углами roll, pitch, yaw и рассчитанными по измерениям датчиков — roll', pitch', yaw'.
3. Результаты — расчет погрешностей оценки углов
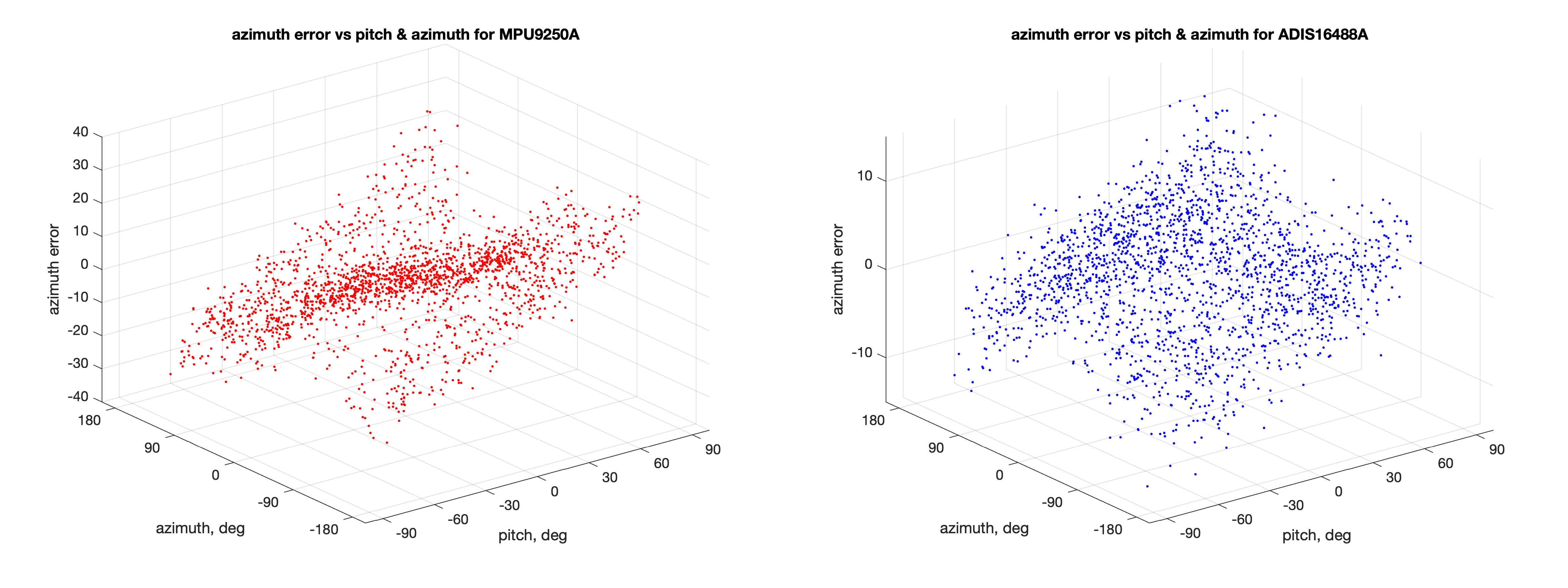
Для двух датчиков, которые мы взяли для примера — ADIS16488A и MPU-9250, получены предельные ошибки оценивания углов ориентации при совместном влиянии погрешностей акселерометра и магнитометра.
В таблице ниже — максимальные значения полученных ошибок:
Совместное влияние погрешностей акселерометра и магнитометра на ошибки оценивания углов ориентации:
- Вот так выглядят ошибки оценивания крена в зависимости от значений крена и тангажа:
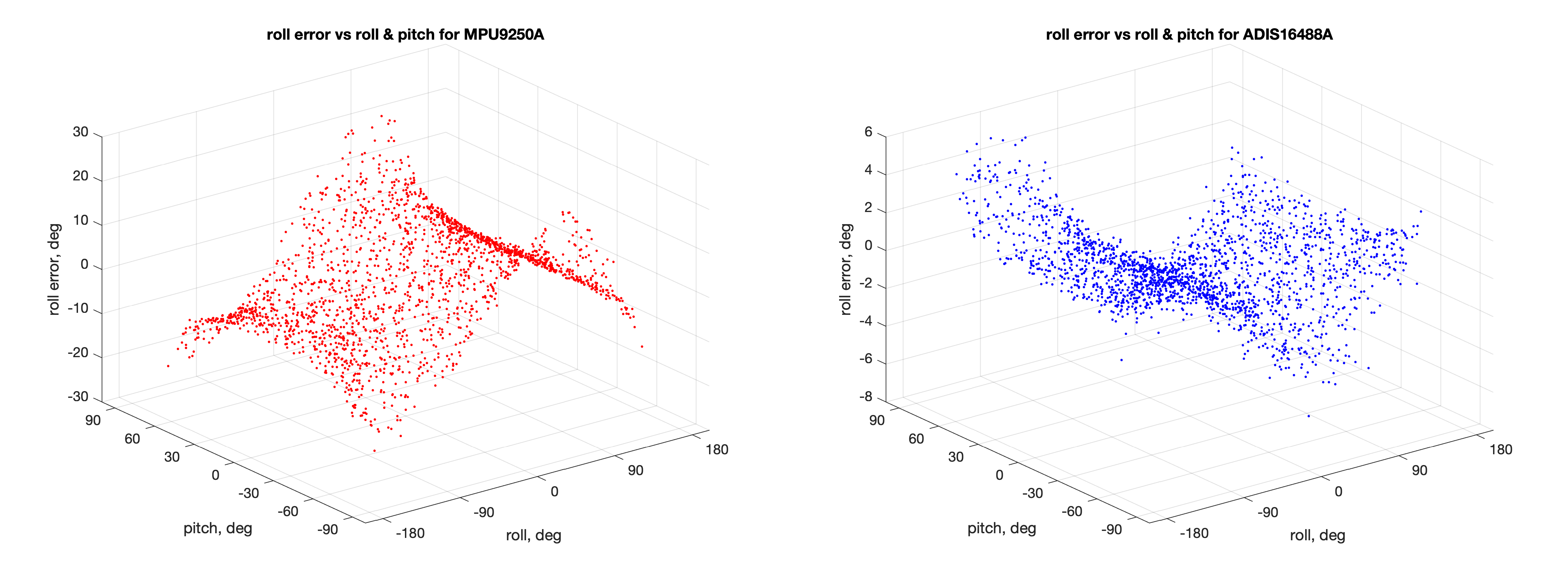
- Ошибки оценивания тангажа в зависимости от значений крена и тангажа:
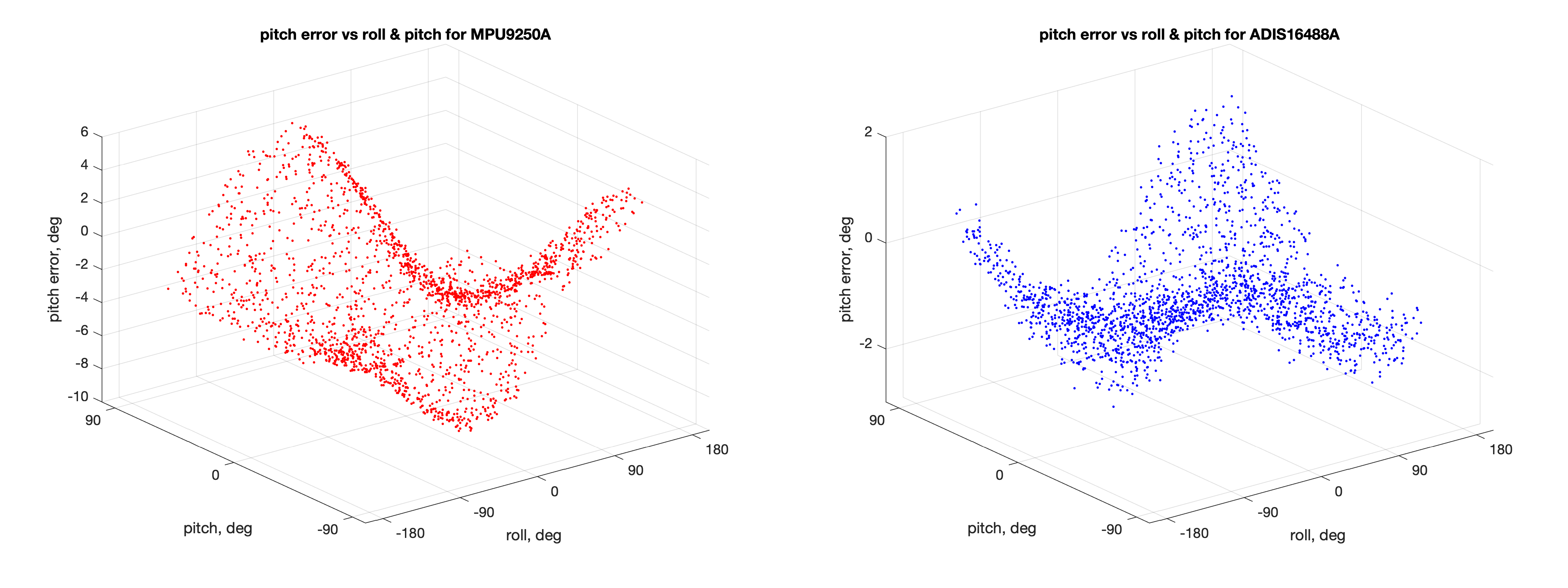
- Ошибки оценивания магнитного азимута от углов крена и тангажа:
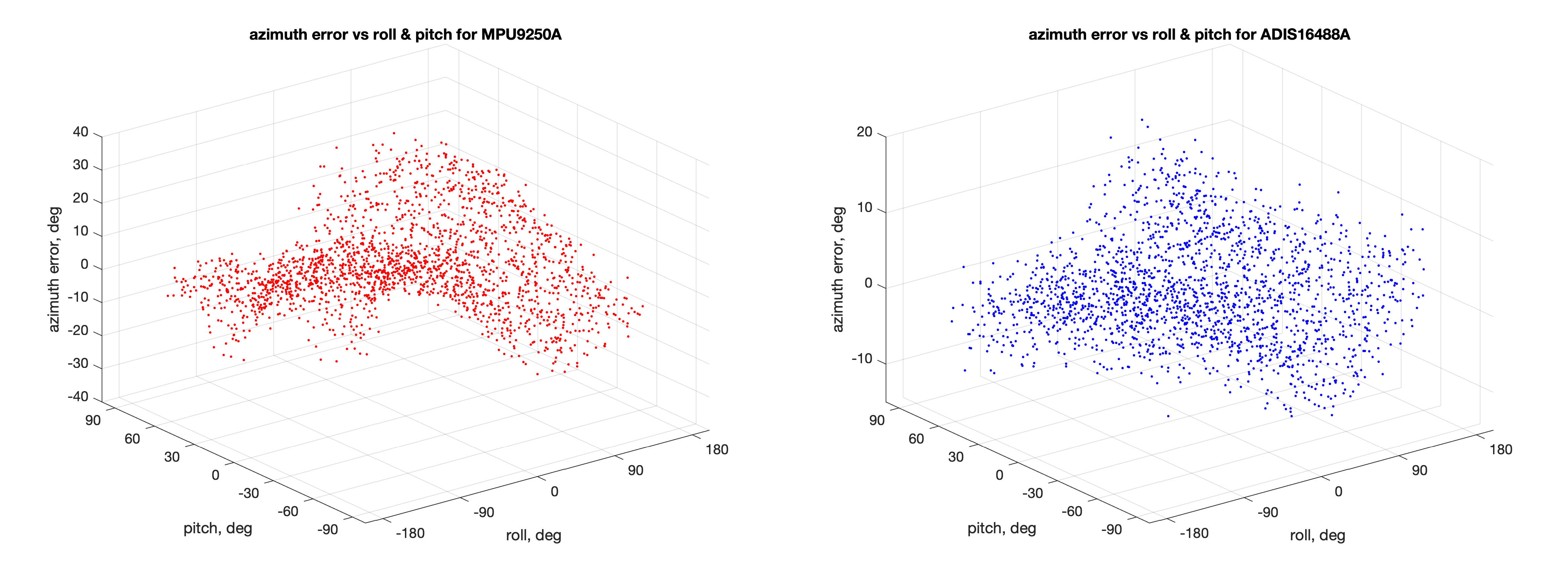
- Ошибки оценивания магнитного азимута от углов крена и магнитного азимута:

- Ошибки оценивания магнитного азимута от углов тангажа и магнитного азимута:
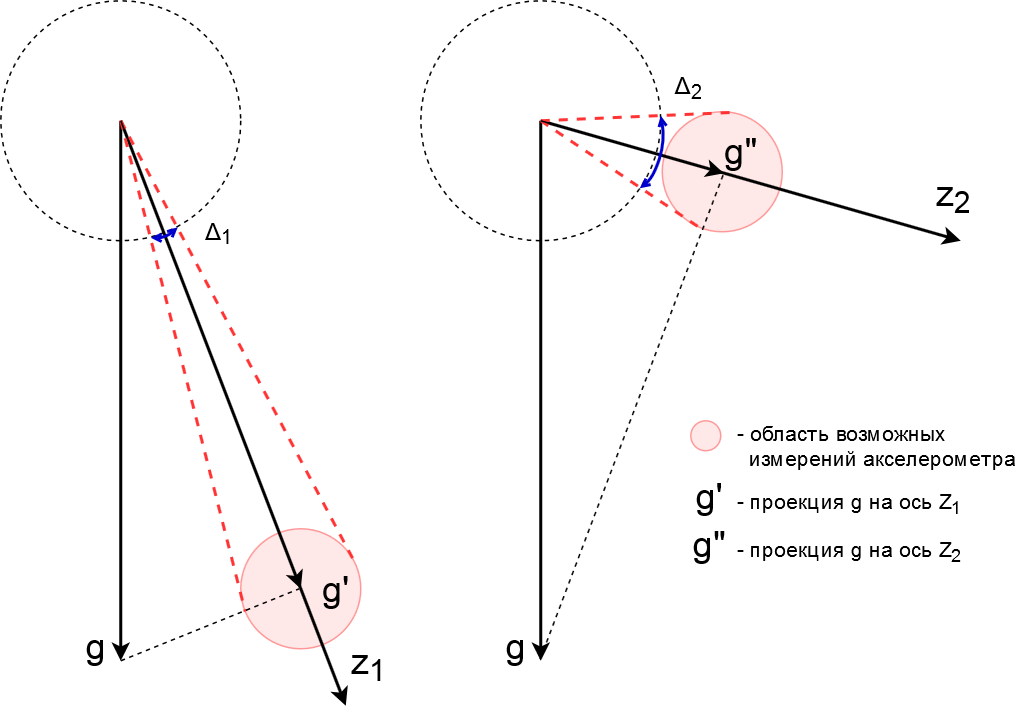
Допустим мы поворачиваем ось чувствительности Z ($inline$z1\rightarrow z2$inline$) акселерометра так, чтобы проекция силы тяжести на эту ось стала меньше ($inline$g'\rightarrow g»$inline$). Значение проекции силы тяжести плюс погрешность акселерометра дадут область возможных значений измерения (розовая область). Погрешность оценки угла при этом возрастает ($inline$\Delta _{1}\rightarrow \Delta _{2}$inline$). Таким образом, при уменьшении проекции вектора силы тяжести на ось чувствительности ошибка акселерометра начинает вносить бОльшую ошибку в оценку угла.
Влияние погрешностей только магнитометра (акселерометр считаем идеальным) на ошибки оценивания углов ориентации:
Итог
- Разработана модель, позволяющая оценивать погрешности расчёта углов ориентации. Углы ориентации рассчитаны по измерениям акселерометров и магнитометров. В расчете погрешности углов учитываются модели погрешностей этих датчиков.
- Ошибки оценивания углов ориентации являются функциями одновременно всех углов ориентации. При этом максимальные значения ошибок наблюдаются на границах диапазонов измерений углов.
- Не рекламируем и не рекомендуем покупать эти датчики (они уже довольно старые).
- Не учитываем влияние нелинейности измерений, влияние вибрации, нестабильности и т.д. — используем лишь первое приближение к модели ошибок датчиков.
