[Из песочницы] Логистика акции по раздельному сбору вторсырья16.06.2019 22:32

Вместо вступления

Когда в России полноценно наладятся процессы сбора и переработки отходов, сказать непросто, а хочется уже сейчас не участвовать в пополнении свалок. Поэтому во многих крупных городах так или иначе существуют волонтерские движения, занимающиеся в частности раздельным сбором.

В Новосибирске такая деятельность формируется вокруг акции «Зеленая белка», в рамках которой раз в месяц обеспокоенные экологией горожане приносят накопленные перерабатываемые бытовые отходы в заранее определенные места в известное время. К этому же времени туда подъезжает арендованный грузовик, который отвозит собранное и рассортированное вторсырье на площадку, откуда оно перераспределяется между различными перерабатывающими предприятиями. Акция существует с 2014 года, и с того времени значительно увеличилось число точек сбора вторсырья, а также его объемы. Для маршрутизации грузовиков одного лишь пристального взгляда стало не хватать, и мы начали разрабатывать оптимизационные модели для минимизации транспортных затрат. Первой из таких моделей и посвящена данная статья.

В разделе 1 я подробно и с иллюстрациями опишу схему организации акции. Далее, в разделе 2, задача минимизации транспортных затрат будет формализована в виде задачи маршрутизации разнородных транспортных средств с временными окнами (heterogenious fleet vehicle routing problem with time windows). Раздел 3 посвящен решению данной задачи с использованием свободно распространяемого пакета для решения смешанно-целочисленных линейных задач математического программирования GLPK.

1. Акция «Зеленая белка»

Начиная с 2014 года инициативная группа «Живая земля» проводит ежемесячную акцию по раздельному сбору вторсырья «Зеленая белка» в Новосибирске. На момент написания статьи к сдаче в переработку с рядом оговорок принимаются пластиковые отходы с маркировкой PET, PE, PP, PS, стекло, алюминий, железо, бытовая техника, макулатура и другое. В подготовке и проведении акции участвует более 50 волонтеров. Акция не является коммерческой, участие в ней бесплатное и не подразумевает денежного вознаграждения.

Точки

Акция проводится в 17 точках города, расположенных друг от друга на расстояниях, преодолеваемых автомобилем за время от 15 до 90 минут. На фото одна из таких точек: слева вдоль стены стоят мешки для сбора различных фракций пластика, справа — грузовик, в который в дальнейшем все грузится, а в центре — волонтер с ушками.

Всю активность на точке организуют кураторы, которые имеют ограничения по времени, в которое они готовы выполнять свои обязанности. При планировании акции кураторы сообщают интервал времени, внутри которого должна пройти акция на их точке.

Также имеются данные по средним объемам вторсырья, собираемым на каждой из точек.

Маршруты

Точки организованы в маршруты, последовательно проезжаемые грузовиком. Перемещения грузовиков контролируются кураторами маршрутов, которые отслеживают оперативную обстановку и принимают решения по обработке особых событий.

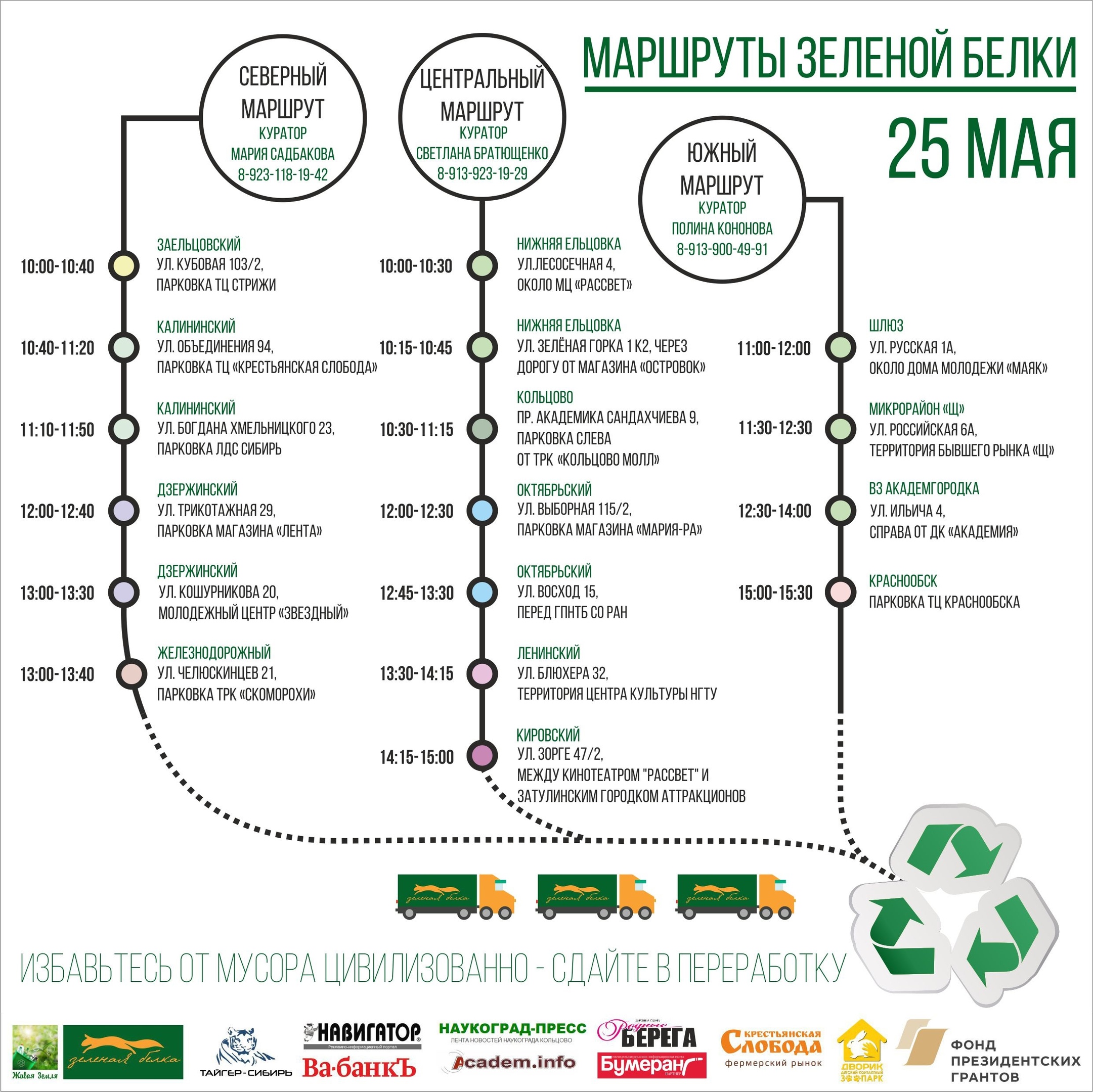
Грузовики

Арендуются на общих основаниях в рамках предложений о почасовой аренде грузового транспорта. Компактизировать пластик на месте не представляется возможным, поэтому основным параметром, характеризующим грузовик, является объем кузова. Грузоподъемность в нашем случае не выступает лимитирующим фактором.

Основные расходы акции связаны именно с оплатой аренды грузовиков, поэтому ее сокращение является критически важным для существования и развития нашей акции, приобретающей институциональное значение в смысле формирования представлений об ответственном потреблении. Далее будет описан подход к решению данного вопроса, основанный на применении методов дискретной оптимизации, а именно математического программирования.

2. Формализация

При построении математической модели будем оставаться в рамках линейных смешанно-целочисленных программ, для понимания которых достаточно знаний алгебры 7 класса.

Единственная сложность может быть связана с использованием абстрактных обозначений и знаков суммирования в формулах. Надеюсь, это не отпугнет читателей, имеющих нечастые встречи с математическими текстами.

В оптимизационной модели можно выделить четыре составные части:

формирование групп точек, составляющих отдельный маршрут;
определение схемы объезда каждой из групп;
удовлетворение требований на время прибытия грузовика на каждую из точек;
определение типа грузовика, необходимого для обслуживания каждого из маршрутов.

Рассмотрим каждую из частей, вводя по мере надобности необходимые обозначения.

Формирование групп точек

Пусть $inline$V = \{1,\dots, n\}$inline$ есть множество индексов точек сбора вторсырья, и площадка, куда собранное вторсырья затем отвозится — будем называть ее депо — имеет индекс 0. Положим $inline$\bar{V} = V\cup \{0\}$inline$

Каждая группа точек формирует отдельный маршрут. Через $inline$R$inline$ обозначим множество номеров маршрутов.

Пусть величина $inline$z_{ir}, i\in I, r\in R$inline$ равняется единице, если точка $inline$i$inline$ включается в маршрут с номером $inline$r$inline$, и нулю в противном случае. Тогда требование о том, что точка $inline$i\in V$inline$ должна войти в один из маршрутов можно записать равенством

$$display$$\sum_{r\in R}z_{ir} = z_{i1} + z_{i2} + \dots + z_{in} = 1.$$display$$

Депо должно войти во все маршруты: $inline$z_{0r} = 1, r\in R$inline$

Тонкости

К сожалению, такая запись создает проблемы вычислительного плана, связанные с симметрией допустимой области. Ее удается устранить, добавив ряд ограничений, обеспечивающих выбор лексикографически минимального разбиения. Подробнее на русском языке об этом можно прочесть, например, тут.

$$display$$1-z_{ir} \leq \sum_{j = 1}^{i-1}\left (1-\sum_{k = 1}^{r-1}z_{jk}\right) + \sum_{k = 1}^{r-1} z_{ik}, \quad i\in I, r\in R, r\leq i.$$display$$

Определение схемы объезда

Маршруты представляют из себя чередующуюся последовательность точек и переездов между ними. Формально все они начинаются в одной из точек множества $inline$V$inline$ и заканчиваются в депо, однако проще будет считать, что все маршруты циклические. Это предположение не меняет сути, но делает все вершины одинаковыми: в этом случае нет концевых вершин, все они транзитные.

Для точек $inline$i, j\in \bar{V}$inline$ и маршрута $inline$r\in R$inline$ заведем переменную $inline$x_{ijr}$inline$, равную единице, если в маршруте c номером $inline$r$inline$ грузовик совершает переезд из точки $inline$i$inline$ в точку $inline$j$inline$, и нулю иначе.

Тогда потребуем, во-первых, чтобы грузовик, двигающийся по маршруту $inline$r\in R$inline$ посещал точку $inline$i\in V$inline$, если она после разделения на группы попала в группу с номером $inline$r$inline$:

$$display$$\sum_{j\in \bar{V}}x_{jir} = z_{ir}, \quad i\in \bar{V}, r \in R.$$display$$

Во-вторых, грузовик после приезда на точку $inline$i\in \bar{V}$inline$ должен с нее выехать.

$$display$$\sum_{j\in \bar{V}}x_{jir} = \sum_{j\in \bar{V}}x_{ijr}, \quad i \in \bar{V}, r\in R.$$display$$

Можно заметить, что данные ограничения позволяют величинам $inline$x_{ijr}$inline$ задавать маршруты, представляющие собой набор непересекающихся циклов. Маршруты такого вида, безусловно, не имеют смысла, и требуется добавить ряд ограничений, чтобы этого избежать.

Об устранении подциклов

Одним из способов может быть введение вспомогательных неотрицательных величин $inline$f_{ijr}, i, j\in \bar{V}, r\in R$inline$ Записанная с использованием данных величин совокупность соотношений устраняет комбинации значений $inline$x_{ijr}$inline$, задающие маршруты, которые не являются связным циклом.

$$display$$\sum_{i\in V}f_{0jr} = \sum_{i\in V}z_{ir}, \quad r \in R,$$display$$

$$display$$f_{ijr}\leq nx_{ijr}, \quad i\in \bar{V}, j \in \bar{V}, r\in R,$$display$$

$$display$$\sum_{j\in \bar{V}}f_{jir} = \sum_{j\in \bar{V}}f_{ijr} + z_{ir}, \quad i\in V, r \in R.$$display$$

Данные соотношения задают поток из точки $inline$v_0$inline$ в остальные точки маршрутов. В каждой промежуточной точке поглощается единица потока, поэтому для того, чтобы в сети существовал поток мощности, равной числу точек минус один, необходимо, чтобы маршрут был связным.

Удовлетворение требований на время прибытия грузовика на каждую из точек

Другими словами, необходимо посещать точки только внутри временных окон, указанных кураторами. Через $inline$B_i$inline$ и $inline$E_i$inline$ обозначим, соответственно, начало и конец временного интервала, в котором куратор точки $inline$i$inline$ может на ней присутствовать.

Для отслеживания выполнения данных ограничений, нам потребуется информация о времени, затрачиваемом грузовиком во время стоянок и переездов на маршруте. Через $inline$L_i, i\in V$inline$ обозначим длительность погрузки на точке $inline$i$inline$, а через $inline$D_{ij}, i, j\in \bar{V}$inline$ — время переезда из точки $inline$i$inline$ в точку $inline$j$inline$ Оговоримся, что $inline$D_{v_0i} = 0$inline$ для всех $inline$i\in \bar{V}$inline$, и в целом может выполняться $inline$D_{ij} \neq D_{ji}$inline$ для любых $inline$i\neq j$inline$

Введем переменные неотрицательные величины $inline$a_i, i\in \bar{V}$inline$ и $inline$w_{ir}, i\in \bar{V}, r\in R$inline$, равные временам прибытия и ожидания на точке $inline$i$inline$ при движении по маршруту $inline$r$inline$, соответственно. Для введенных величин должны выполняться следующие соотношения.

Время ожидания не может быть меньше времени, требуемого для погрузки

$$display$$w_{ir}\geq L_iz_{ir}, \quad i\in \bar{V}, r\in R,$$display$$

и равно нулю, если точка не относится к маршруту $inline$r$inline$

$$display$$w_{ir}\leq Mz_{ir}, \quad i\in \bar{V}, r\in R,$$display$$

Время прибытия на точку $inline$j$inline$ вычисляется через соответствующие времена для предшествующей точки $inline$i$inline$ Здесь достаточно большая константа $inline$M$inline$ используется для устранения ненужных зависимостей в случае, когда переезд между $inline$i$inline$ и $inline$j$inline$ не совершается.

$$display$$a_i + \sum_{r\in R}w_{ir} + D_{ij}\leq a_j + M (1 — \sum_{r\in R}x_{ijr}), \quad i\in I, j\in V,$$display$$

Прибытие и отправление грузовика должны находиться внутри обозначенного куратором интервала.

$$display$$a_i\geq B_i, \quad i\in V,$$display$$

$$display$$a_i + \sum_{r\in R}w_{ir}\leq E_i, \quad i\in V.$$display$$

Определение типа грузовика, необходимого для обслуживания каждого из маршрутов
Обозначим множество типов грузовиков, доступных для аренды, через $inline$T$inline$ Грузовик типа $inline$t\in T$inline$ характеризуется объемом кузова $inline$C_t$inline$ и стоимостью часовой аренды $inline$P_t$inline$ Минимальное время аренды грузовика типа $inline$t$inline$ обозначим через $inline$U_t^0$inline$ Объем вторсырья, собираемый на точке $inline$i\in V$inline$ обозначим через $inline$G_i$inline$

Введем переменные величины $inline$y_{tr}, t\in T, r\in R$inline$, равные единице, если грузовик типа $inline$t$inline$ назначается на обслуживание маршрута с номером $inline$r$inline$, и нулю иначе.

Целочисленные переменные $inline$u_{tr}, t\in T, r\in R$inline$ задают время аренды грузовика типа $inline$t$inline$, обслуживающего маршрут с номером $inline$r$inline$
Для каждого маршрута, $inline$r\in R$inline$, необходимо назначить тип грузовика:

$$display$$\sum_{t\in T}y_{tr} = 1, \quad r\in R$$display$$

В соответствии с разбиением точек между маршрутами, некоторые маршруты могут оказаться тривиальными, то есть содержать только депо. Если маршрут $inline$r$inline$ нетривиальный, то грузовик, назначенный на него, арендуется не менее чем на $inline$U_t^0$inline$ часов.

$$display$$u_{tr}\geq U_t^0 (y_{tr} — \sum_{i\in V}z_{ir}), \quad t\in T, r\in R.$$display$$

В то же время, длительность аренды должна превосходить также суммарную длительность стоянок и переездов в маршруте.

$$display$$u_{tr}\geq \sum_{i\in V}\sum_{j\in \bar{V}}D_{ij}x_{ijr}+\sum_{i\in \bar{V}}w_{ir}-M (1-y_{tr}), \quad r\in R, t\in T.$$display$$

Добавим ограничения обеспечивающие свойство: если грузовик типа $inline$t$inline$ не назначен на маршрут $inline$r$inline$, время его аренды равно нулю.

$$display$$u_{tr}\leq My_{tr}.$$display$$

Все вторсырье, собранное на точках маршрута, должно поместиться в кузове грузовика.

$$display$$\sum_{i\in V}G_iz_{ir}\leq \sum_{t\in T}C_ty_{tr}, \quad r\in R.$$display$$

Наконец, наша цель состоит в минимизации затрат на аренду грузовиков, которая с помощью введенных обозначений записывается как $inline$\sum_{t\in T}\sum_{r\in R}P_tu_{tr}$inline$

Поиск решения

Несложно убедиться в том, что все выражения, участвующие в оптимизационной модели, являются линейными функциями от переменных величин, поэтому для нахождения точного и приближенных решений можно пользоваться стандартными пакетами для решения задач смешанно-целочисленного программирования таких, как Gurobi, CPLEX, Xpress, ORtools, SCIP, BLIS и т.д.
Запишем модель минимизации транспортных затрат на языке GMPL. Это позволит использовать для наших целей свободно распространяемый пакет GLPK. Для написания кода и отладки модели удобно будет скачать среду разработки GUSEK, которая уже содержит GLPK в своем составе.

Выглядит GUSEK следующим образом:

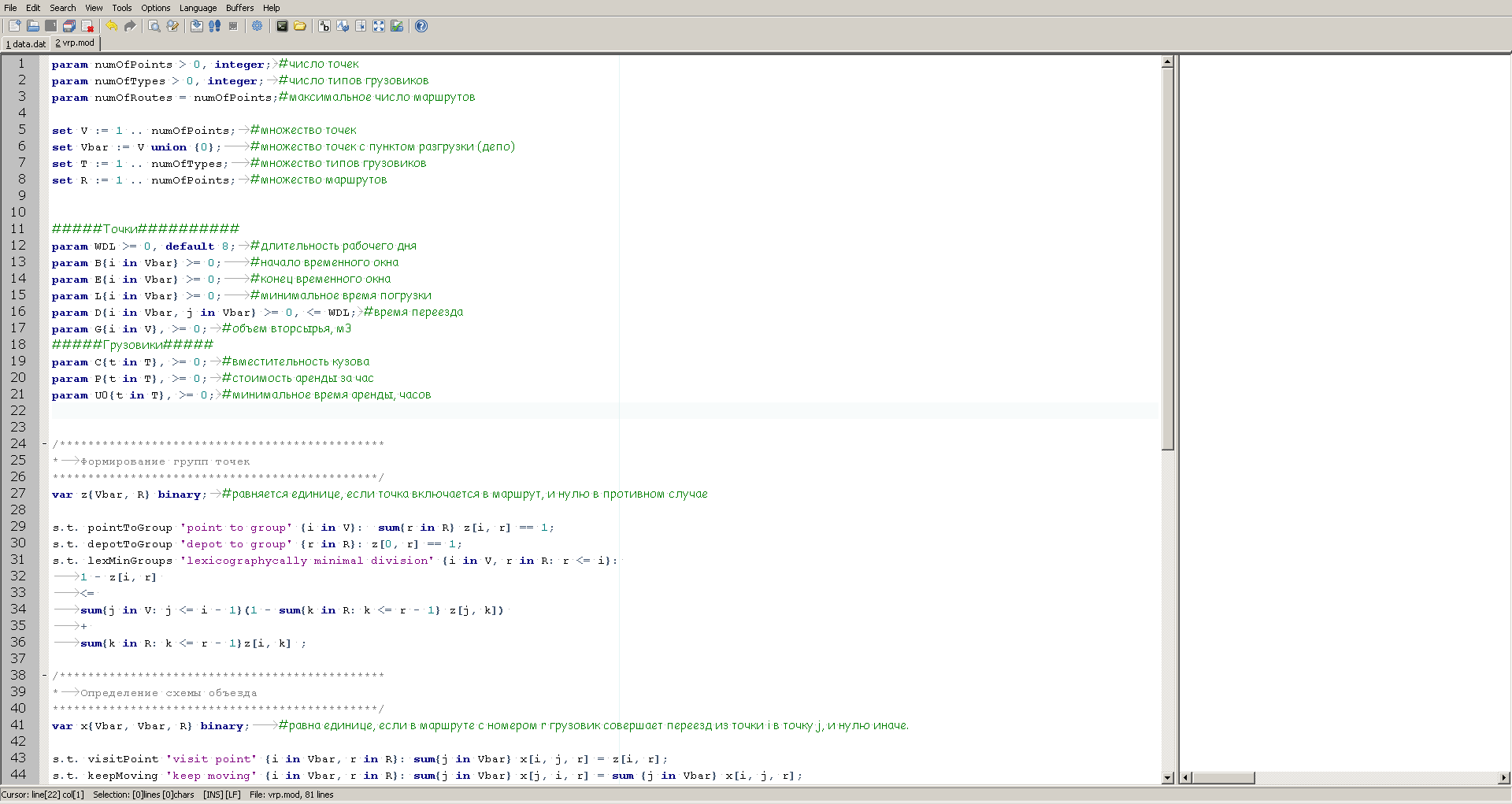
Слева мы видим описание модели, а справа окошко вывода информации о ходе вычислений, которую будет поставлять решатель после запуска.

Полное описание модели

param numOfPoints > 0, integer;	#число точек
param numOfTypes > 0, integer;	#число типов грузовиков
param numOfRoutes = numOfPoints;#максимальное число маршрутов

set V := 1 .. numOfPoints;	#множество точек
set Vbar := V union {0};	#множество точек с пунктом разгрузки (депо)
set T := 1 .. numOfTypes;	#множество типов грузовиков
set R := 1 .. numOfPoints;	#множество маршрутов


#####Точки##########
param WDL >= 0, default 8;	#длительность рабочего дня
param B{i in Vbar} >= 0;	#начало временного окна
param E{i in Vbar} >= 0;	#конец временного окна
param L{i in Vbar} >= 0;	#минимальное время погрузки
param D{i in Vbar, j in Vbar} >= 0, <= WDL;	#время переезда
param G{i in V}, >= 0;	#объем вторсырья, м3
#####Грузовики#####
param C{t in T}, >= 0;	#вместительность кузова
param P{t in T}, >= 0;	#стоимость аренды за час
param U0{t in T}, >= 0;	#минимальное время аренды, часов


/**********************************************
*	Формирование групп точек
**********************************************/
var z{Vbar, R} binary;	#равняется единице, если точка включается в маршрут, и нулю в противном случае

s.t. pointToGroup 'point to group' {i in V}:  sum{r in R} z[i, r] == 1;
s.t. depotToGroup 'depot to group' {r in R}: z[0, r] == 1;
s.t. lexMinGroups 'lexicographycally minimal division' {i in V, r in R: r <= i}: 
	1 - z[i, r] 
	<= 
	sum{j in V: j <= i - 1}(1 - sum{k in R: k <= r - 1} z[j, k]) 
	+ 
	sum{k in R: k <= r - 1}z[i, k] ;

/**********************************************
*	Определение схемы объезда
**********************************************/
var x{Vbar, Vbar, R} binary;	#равна единице, если в маршруте c номером r грузовик совершает переезд из точки i в точку j, и нулю иначе.

s.t. visitPoint 'visit point' {i in Vbar, r in R}: sum{j in Vbar} x[i, j, r] = z[i, r];
s.t. keepMoving 'keep moving' {i in Vbar, r in R}: sum{j in Vbar} x[j, i, r] = sum {j in Vbar} x[i, j, r];

var f{Vbar, Vbar, R} >= 0;		#Потоки, устраняющие подциклы.

s.t. flowFromDepot 'flow from depot' {r in R}: sum{i in V} f[0, i, r] == sum{i in V} z[i, r];
s.t. flowAlongActiveArcs 'flow along active arcs' {i in Vbar, j in Vbar, r in R}: f[i, j, r] <= numOfPoints * x[i, j, r];
s.t. flowConservation 'flow conservation' {i in V, r in R}: sum{j in Vbar} f[j, i, r] == sum{j in Vbar} f[i, j, r] + z[i, r];

var a{i in V} >= 0;	#время прибытия грузовика на точку
var w{i in Vbar, r in R} >= 0;	#время нахождения грузовика на точке

s.t. wait 'wait'{i in Vbar, r in R}: w[i, r] >= L[i] * z[i, r];
s.t. dontWait 'dont wait'{i in Vbar, r in R}: w[i, r] <= (E[i] - B[i]) * z[i, r];
s.t. arrivalTime 'arrival time' {i in V, j in V}: a[i] + sum{r in R}w[i, r] + D[i,j] <= a[j] + 3 * WDL * (1 - sum{r in R} x[i, j, r]);
s.t. arriveAfter 'arrive after' {i in V}: a[i] >= B[i];
s.t. departBefore 'depart before' {i in V}: a[i] + sum{r in R}w[i, r] <= E[i];

/**********************************************
*	Определение типа грузовика, необходимого для обслуживания каждого из маршрутов
**********************************************/

var y{t in T, r in R}, binary;	#равные единице, если грузовик типа t назначается на обслуживание маршрута с номером r, и нулю иначе.
var u{t in T, r in R}, integer, >= 0;	#время аренды грузовика типа t, обслуживающего маршрут с номером r.

s.t. assignVehicle 'assign vehicle' {r in R}: sum{t in T} y[t,r] == 1;
s.t. rentTime 'rent time' {r in R, t in T}: u[t, r] >= sum{i in V, j in Vbar}D[i, j] * x[i, j, r] + sum{i in Vbar}w[i, r] - WDL * (1 - y[t, r]);
s.t. minRentTime 'minimal rent time' {r in R, t in T}: u[t, r] >= U0[t] * (y[t, r] - sum{i in V}z[i, r]);
s.t. noRent 'no rent' {t in T, r in R}: u[t, r] <= WDL * y[t, r];
s.t. fitCapacity 'fit capacity' {r in R}: sum{i in V} G[i] * z[i, r] <= sum{t in T} C[t] * y[t, r];

minimize rentCost: sum{t in T, r in R} P[t] * u[t, r];

solve;

/**********************************************
*	Вывод решения на экран
**********************************************/
printf{i in V, r in R} (if 0.1 < z[i,r] then "point %s to group %s\n" else ""), i, r, z[i,r];
printf{r in R, i in Vbar, j in Vbar} (if 0.1 < x[i, j, r] then "route %s: %s -> %s\n" else ""), r, i, j;
printf{i in V} "point %s arrive between %s and %s (actual = %s)\n", i, B[i], E[i], a[i];
end;

Для быстрого старта добавлю также подготовленные для использования в модели данные, взятые из головы:

Входные данные

data;

param numOfPoints := 9;	#число точек
param numOfTypes := 6;	#число типов грузовиков


#####Точки##########
param 	:	B	E	L :=
		0	0	8	1
		1	0	8	1
		2	0	8	1
		3	0	8	1
		4	0	8	1
		5	0	8	1
		6	0	8	1
		7	0	8	1
		8	0	8	1
		9	0	8	1;
param D default 0
:	0	1	2	3	4	5	6	7	8	9 :=
0	.	.	.	.	.	.	.	.	.	.
1	0.1	0.3	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
2	0.3	0.2	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
3	0.4	0.3	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
4	0.4	0.4	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
5	0.1	0.2	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
6	0.5	0.5	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
7	0.3	0.2	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
8	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1
9	0.5	0.2	0.2	0.1	0.2	0.1	0.2	0.1	0.2	0.1;
param 	G	:=
	1	1
	2	2
	3	1
	4	2
	5	1
	6	2
	7	1
	8	2
	9	1;
#####Грузовики#####
param 	:	C	P :=
		1	8	500
		2	10	500
		3	14	600
		4	18	650
		5	25	700
		6	35	800;
param U0 default 2;	#минимальное время аренды, часов

end;

После копирования кода модели в файлик с именем, к примеру, model.mod, а входные данные — в файлик data.dat, все готово к запуску. Установим ограничение на время вычисления 100 секунд (это делается с помощью ключа --tmlim [время в секундах]), передадим путь к файлу с входными данными (с помощью ключа -d [путь к файлу]),

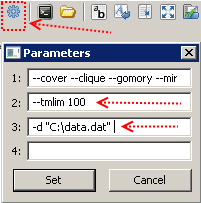
и жмем F5. В случае успеха в окне справа начнут появляться сообщения, и через сто секунд у нас на руках будет лучшее решение, которое GLPK успел найти за отведенное время.

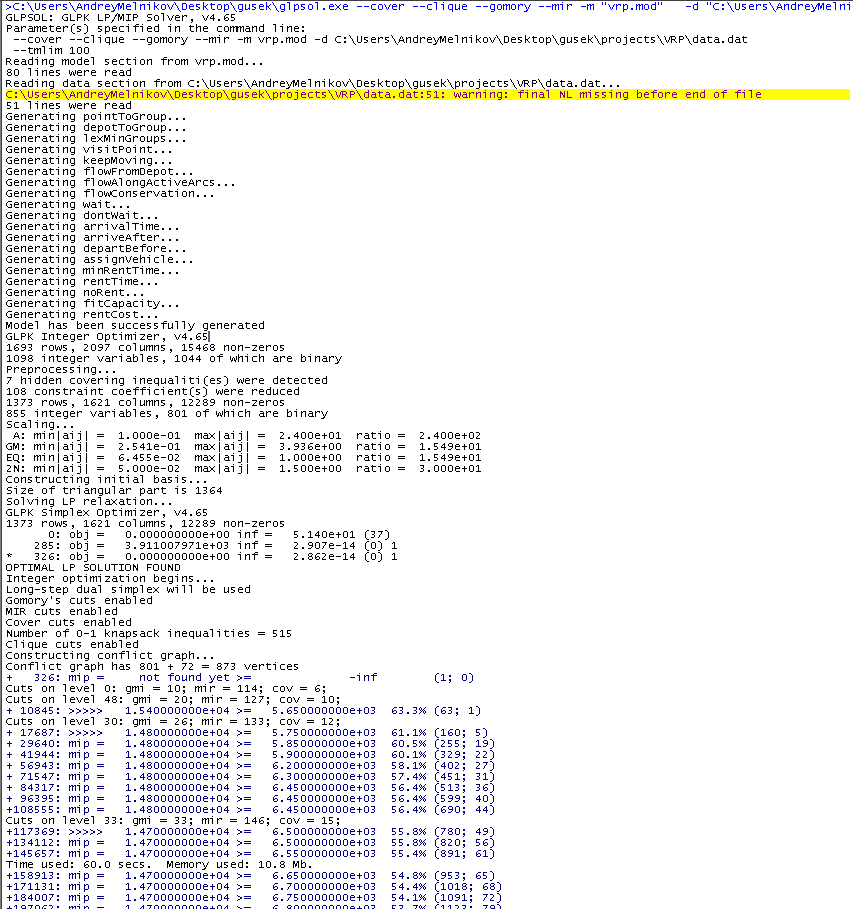
В синем тексте нас интересует значение после надписи «mip = ». Как видно, оно время от времени уменьшается. В процессе работы находятся все новые решения, значение транспортных затрат на лучшем из которых выводится в этом столбце (пока там 14700). Следующее число — это оценка снизу для наилучшего существующего, т. е. оптимального решения. Изначально оценка ощутимо занижена, но со временем уточняется, то есть возрастает. Значения слева и справа сближаются, и относительный разрыв между ними на момент скриншота составляет 54.1%. Как только это число станет равным нулю, алгоритм докажет, что лучшее найденное решение является наилучшим возможным. Дожидаться этого события на практике не всегда оправданно, и не только потому, что это долго, однако важно оговориться, что как правило, хорошее решение находится относительно быстро, и основные временные затраты связаны с уточнением оценки, требуемым для доказательства неулучшаемости.

Вместо заключения

Задачи маршрутизации крайне сложны в вычислительном плане, и с ростом числа точек, которые требуется посетить, время, необходимое решателю для нахождения решения и доказательства его оптимальности, стремительно растет. Однако для достаточно небольших примеров решатель за приемлемое время способен построить удачный набор маршрутов и может использоваться для поддержки принятия решений. Анализ предлагаемых моделью вариантов маршрутизации помог нам обнаружить существенные возможности для сокращения затрат, и это критически важно для существования и развития акции.

Наши дальнейшие усилия направились в сторону работы с неопределенностью в объемах вторсырья, собираемых на точках. Мы разрабатываем ряд моделей стохастического программирования для принятия стратегических и оперативных решений в маршрутизации грузовиков. Если тема окажется актуальной и вызовет интерес — напишу и об этом тоже, ведь скоро всем нам придется значительно основательнее погрузиться в решение экологических вопросов, в чем и желаю нам успехов.