[Из песочницы] Анализ эффективности метода факторизации на эллиптических кривых. Практика
Приведём определение факторизации.
Факторизацией целого числа называется его разложение в произведение простых сомножителей. Такое разложение, согласно основной теореме арифметики, всегда существует и является единственным (с точностью порядка следования множителей).
Будем обозначать число, которое требуется разложить буквой N, а два сомножителя, в результате умножения которых получим N, как a и b.
Алгоритм факторизации Ленстры (факторизация на эллиптических кривых) является одним из самых быстрых методов факторизации. Он имеет много общего с методом Полларда (p — 1), но работает значительно быстрей, следует отметить, что он является субэкспоненциальным методом. Главная особенность алгоритма — это то, что время, затраченное на факторизацию, зависит не от размерности N, а от размера наименьшего делителя числа N.
Подробно про этот метод вы сможете почитать из материала в списке использованной литературы, но всё же приведём основные стадии алгоритма.
- Введём число N.
- Выберем некоторое значение B, которое является максимальным пределом числа-делителя N.
- Сгенерируем случайным образом значения x, y, a, которые принадлежат множеству целых чисел от 0 до N-1. Эти значения определяют кривую, а так же x и y определяют начальную точку P.
- Вычислим b = y^2-x^3-ax mod n и g = Н.О. Д.(N, 4a^3+27b^2). Важно, что бы g не был равен N, иначе возвращаемся к п.2. Если 1 < g < n, тогда прекратим вычисление – делитель найден. Этот вариант возможен при малых значениях числа N (например 10), при возрастании N эта возможность встречается всё реже.
- Далее нужно выполнить цикл, в результате которого для каждого простого числа p (в пределе от 2 до B-1) вычислим точку P, домноженную на p^r, где r наибольшая степень, удовлетворяющая условию p^r < B.
В арифметике полей нет операции деления, которая необходима в формулах для нахождения координат точек, так что мы преобразуем выражение в виде умножения, а обратный элемент ищем по расширенному алгоритму Евклида. К тому же каждое новое вычисление мы производим по модулю числа N.
Алгоритм завершит свою работу, когда будет найден Н.О. Д.(N, P), который больше 1 и меньше N. Во избежание ошибки в ответе, функция нахождения Н.О. Д. должна проверять только положительные значения.
Рассмотрим график времени, которое нам понадобится для факторизации разных чисел. (Результат приведён из написанной мною программы)
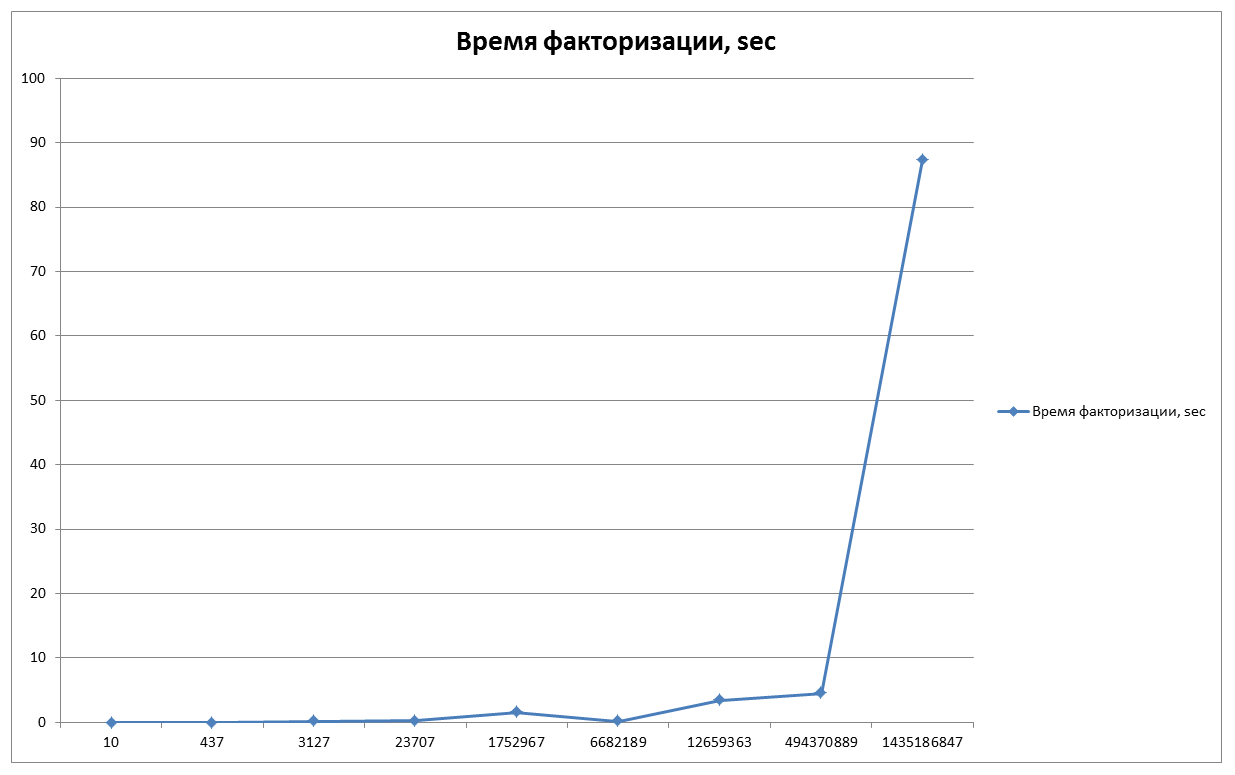
N=10 — 0,005 sec;
N=437 — 0,019 sec;
N=3127 — 0,055 sec;
N=23707 — 0,191 sec;
N=1752967 — 1,534 sec;
N=6682189 — 0,143 sec;
N=12659363 — 3,376 sec;
N=494370889 — 4,484 sec;
N=1435186847 — 87,377 sec;
Так как кривая генерируется из случайных значений, то время факторизации при каждом новом запуске программы будет разным. Смотря удачная ли кривая нам попадётся. По этому, попробуем взять эти же числа и выполнить факторизацию ещё несколько раз и сверим результаты.
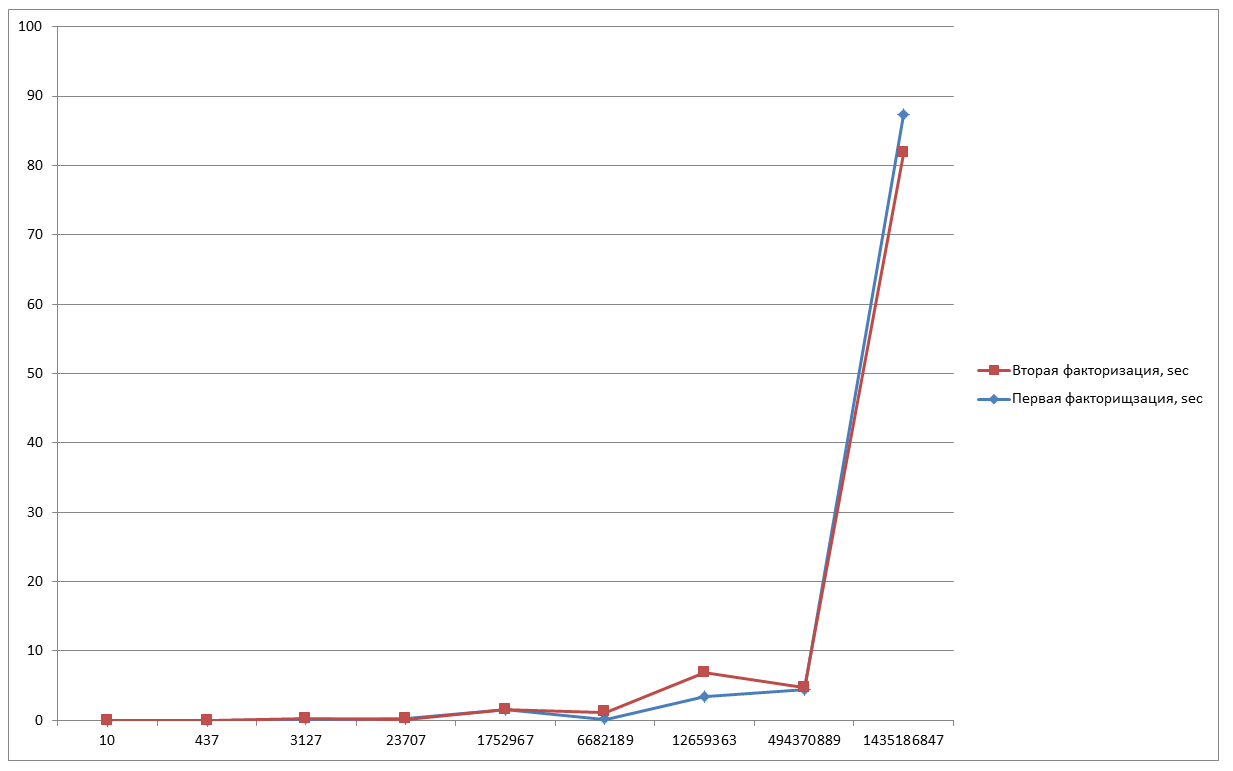
N=10 — 0,016 sec;
N=437 — 0,016 sec;
N=3127 — 0,218 sec;
N=23707 — 0,079 sec;
N=1752967 — 1,484 sec;
N=6682189 — 1,125 sec;
N=12659363 — 6,906 sec;
N=494370889 — 4,781 sec;
N=1435186847 — 81,766 sec;
И для закрепления сделаем последний замер.
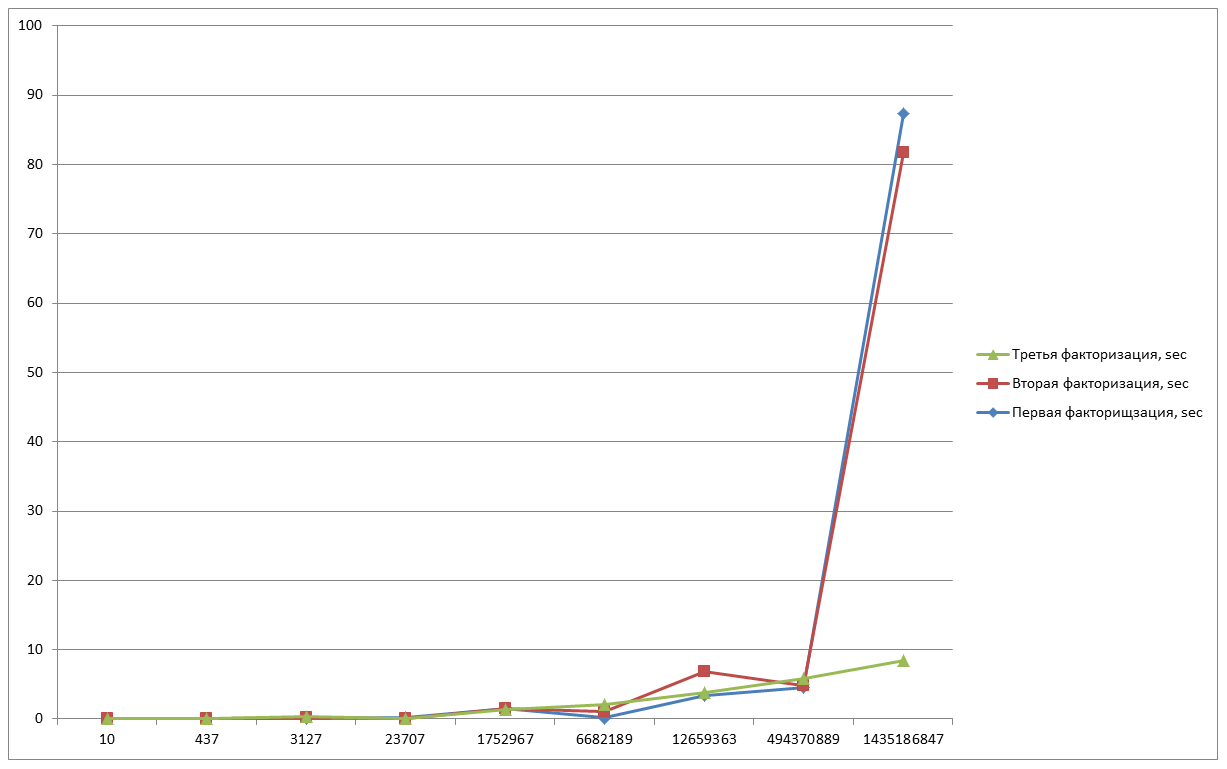
N=10 — 0,012sec;
N=437 — 0,022 sec;
N=3127 — 0,156 sec;
N=23707 — 0,205 sec;
N=1752967 — 1,418 sec;
N=6682189 — 1,056 sec;
N=12659363 — 0,25 sec;
N=494370889 — 5,488 sec;
N=1435186847 — 14,117 sec;
Как мы видим на последнем графике, время затраченное на последнее число заметно уменьшилось, это характеризуется тем, что кривая генерируется случайным образом. Следует заметить, что время, затраченное на выполнение алгоритма, зависит и от значения B, которое мы вводим. Я старался брать значение приближённые к значениям двух сомножителей (a и b), но если вы будете выполнять операцию над числом, где изначальные множители не известны даже приблизительно, то стоит выбирать предел выше. Но чем выше предел, тем больше и времени уйдёт на вычисление точек, потому что их будет больше, это нужно учитывать.
Следует учитывать и производительность вычислительной машины. Я производил вычисления на Процессоре AMD Athlon™ II X4 645 с частотой 3.10 ГГц. Нагрузка на Процессор была около 40% при работе программы. Нагрузки на Память замечено не было.
Итог
Алгоритм работает за достаточно хорошее время, но только для относительно не больших значений. Ведь как мы видим по графику 1 и 2, число после 1 миллиарда в большинстве случаев имеет большой разрыв со временем, затраченное на число 494370889, но это было ожидаемо, ведь как было замечено ранее, метод является субэкспоненциальным.
Спасибо, что дочитали мою первую статью.
Использованная литература: «Математические основы защиты информации»
Комментарии (5)
9 февраля 2017 в 15:12 (комментарий был изменён)
+2↑
↓
Вы бы хоть программу показали, это же Хабр, а не защита курсовой.
Ну и по-хорошему для анализа эффективности программу нужно запустить не три раза, а три тысячи раз и привести один усреднённый график.
P.S. С недавнего времени Хабр может в формулы.9 февраля 2017 в 15:41
0↑
↓
Спасибо за комментарий, буду стремиться не допускать больше таких недочётов. А что насчёт программы, так у меня были сомнения по поводу нужна ли она здесь, так как это уже отдельная тема.
9 февраля 2017 в 15:55
0↑
↓
Как оценивали нагрузку на память?9 февраля 2017 в 16:04
0↑
↓
Я не делал тщательный анализ нагрузки на память, я лишь следил за производительностью и монитором ресурсов в Windows. В общем счёте программа занимает 0,4 МБ памяти в любой момент времени работы. И я сделал вывод, что нагрузки, как таковой, на память нет.
9 февраля 2017 в 16:59
0↑
↓
Статья хоть и короткая, но хорошая для первого раза. Но с точки зрения выводов и информативности ниочём.
