#4 Нейронные сети для начинающих. Sudoku Solver. Судоку. Часть 120.12.2022 19:17

Предыстория: одним зимним вечером, а скорее ночью, мне пришла в голову интересная идея. Почему бы не попробовать автоматизировать с помощью компьютерного зрения решение одной классической головоломки с числами, а если быть точнее — судоку. Дело в том, что мой дедушка — большой любитель разных кроссвордов, судоку и т. д. Зная это, я подумал, что было бы неплохо попробовать как-нибудь автоматизировать эту задачу. Конечно, до задачи автоматизации решения кроссвордов мне ещё далеко, но вот с задачей решения судоку, у которого есть чёткий алгоритм, можно поэкспериментировать.

Спойлер: я столкнулся с парой проблем как в своём понимании этой игры, так и в понимании меня компьютером (тут должно было быть смешно), но всё получилось. С результатом моего труда я вам и предлагаю ознакомиться!

Но перед всем этим я советую вам прочитать мои предыдущие статьи из серии «Нейронные сети для начинающих». Там их уже целых три:

▍ Немного теории

Итак, приступим, но для начала давайте разберёмся, что же такое Судоку.

Согласно Википедии, Судо́ку (от японского 数独 су: доку) — это головоломка с числами. Иногда судоку называют магическим квадратом, что в общем-то неверно, так как судоку является латинским квадратом 9-го порядка. Судоку активно публикуют газеты и журналы разных стран мира, сборники судоку издаются большими тиражами. Решение судоку — популярный вид досуга.

А как судоку появилась?

В XVIII веке Леонард Эйлер изобрёл игру Carré latin («Латинский квадрат»). На основе этой игры в 1970-х годах в Северной Америке были придуманы специальные числовые головоломки. Так, в США судоку появилась впервые в 1979 году в журнале Dell Puzzle Magazine. Тогда она называлась Number Place. Настоящую популярность судоку завоевала в 1980—1990-х годах, когда японский журнал Nikoli начал регулярно публиковать на своих страницах эту головоломку (с 1986 года). Сегодня судоку — обязательный компонент многих газет. Среди них много изданий с многомиллионными тиражами, например, немецкая газета Die Zeit, австрийский Der Standard. В России судоку также публикуются в десятках газет, журналов и в специализированных сборниках.

Хорошо, а что там с правилами игры? Давайте разберёмся:

Игровое поле представляет собой квадрат размером 9×9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В них уже в начале игры стоят некоторые числа (от 1 до 9), называемые подсказками. От игрока требуется заполнить свободные клетки цифрами от 1 до 9 так, чтобы в каждой строке, в каждом столбце и в каждом малом квадрате 3×3 каждая цифра встречалась бы только один раз. Сложность судоку зависит от количества изначально заполненных клеток и от методов, которые нужно применять для её решения. Самые простые решаются дедуктивно: всегда есть хотя бы одна клетка, куда подходит только одно число. Некоторые головоломки можно решить за несколько минут, на другие можно потратить часы.
Правильно составленная головоломка имеет только одно решение. Тем не менее, на некоторых сайтах в интернете под видом усложнённых головоломок пользователю предлагаются варианты судоку с несколькими вариантами решения, а также с ветвлениями самого хода решения.

Как я понял, задача обобщённого судоку на поле N2 * N2 является NP-полной, так как к ней сводится задача о заполнении латинского квадрата.

Количество различных судоку классического размера 9×9 с однозначным решением равно 6670903752021073000000 (последовательность A107739 в OEIS) — данные взяты из Википедии, или примерно 6.67 на 10 в 21-й степени. Однако если считать одинаковыми те судоку, которые получаются друг из друга с помощью поворотов, отражений и перенумерации, то это количество уменьшается до 5 472 730 538 (последовательность A107739 в OEIS).

Долгое время оставался открытым вопрос о минимальном количестве подсказок, необходимых для решения судоку. В частности, не было известно, существует ли однозначно решаемый судоку с 16 подсказками. Проект распределённых вычислений Sudoku@vtaiwan на платформе BOINC занимался поиском такого. В январе 2012 года появилось доказательство того, что однозначно решаемых судоку с 16 подсказками не существует.

Итак, мы выяснили, что такое судоку и что существует по сути только 2 правила при решении этой головоломки:

Игровое поле можно заполнять только цифрами от 1 до 9. Существуют виды судоку, которые решают буквами или символами, но это совершенно отдельные игры со своими правилами и стратегией.
Цифру можно записывать лишь в том случае, если она не будет повторяться в строке, столбце и малом квадрате 3×3, в которых расположена пустая ячейка.

Существует множество способов решения этой головоломки, но больше всего мне понравился метод решения с помощью анализа малых квадратов. Давайте подробнее разберём именно его.
Рассмотрите каждый малый квадрат и выпишите рядом с ним все цифры, которых в нём не хватает.

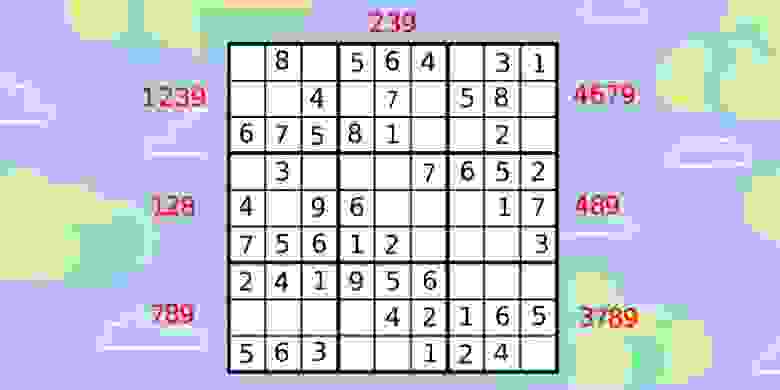
Выберите одну из фигур, в которой не заполнено меньше всего ячеек. Положим, левый центральный квадрат. Там нет цифр 1, 2 и 8.

Сразу заметно, что 2 не может стоять ни в одной из свободных ячеек в верхней строке, ведь там уже есть двойка. Значит, расположение этой цифры однозначно.

Остаются только две клетки в верхней строке малого квадрата. Но 1 не может находиться в правой ячейке, поскольку уже есть во всём столбце. Поэтому ставим туда 8. Получается, для единицы доступно только одно место:

Рассмотрите следующую фигуру. Например, левую нижнюю, где не хватает трёх цифр — 7, 8 и 9. Теперь расставляем цифры в допустимые для них ячейки.

Берём 7. Она не должна стоять ни в первом, ни во втором столбце, поскольку в каждом из них уже есть семёрка. Значит, эту цифру можно вписать только в третий столбец.

Переходим к 8. Она не может находиться во втором столбце, потому что уже стоит в нём. Соответственно, единственное допустимое для этой цифры место — первый столбец.

Цифру 9 по остаточному принципу ставим в единственную свободную ячейку — в центральном втором столбце:

Пример выше взят отсюда, там же можно посмотреть другие примеры решения судоку.

▍ Шаг 1. Начинаем работу

Разобравшись с основной историей и теорией этой потрясающей по своей сути головоломки, приступим к работе над её решением с точки зрения кода.

В первую очередь нам понадобится поле для судоку, на котором мы сможем тестировать наш алгоритм. Я взял 4 варианта этой головоломки (разных цветов и размеров):

Для себя я выработал следующий алгоритм работы с изображениями:

Предварительная обработка.
Нахождение контуров.
Нахождение поля судоку.
Классификация цифр или банальный поиск их на игровом поле.
Поиск решения судоку.
Наложение решения на изначальное изображение.

Во-первых, нам необходимо прописать путь к изображению (моё изображение находится в папке с проектом, поэтому я пишу только его название):

pathImage = 'Sudoku_test_1.png' # Путь до тестового изображения

И вот что находится по этому пути:

Далее перейдём к подготовке изображения (смотрите комментарии к коду), но перед этим импортируем библиотеки и файлы:

import cv2
import numpy as np
from utlis import *

# Подготовка изображения
heightImg = 450
widthImg = 450
img = cv2.imread(pathImage) # Считываем изображение по нашему пути
img = cv2.resize(img, (widthImg, heightImg)) # Используем функцию изменения размера изображения, под необходимые нам
imgBlank = np.zeros((heightImg, widthImg, 3), np.uint8) 
imgTreshold = preProcess(img) # Здесь мы используем самописную функцию из файла "utlis.py"

Функция preProcess ():

# Подготовка изображения
def preProcess(img):
    imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Конвертация в оттенки серого
    imgBlur = cv2.GaussianBlur(imgGray, (5, 5), 1) # Добавляем Гаусианов Блюр
    imgTreshold = cv2.adaptiveTreshold(imgBlur, 255, 1, 1, 11, 2) # Добавляем адаптивный трешхолд
    return imgTreshold

Функция stackImages ():

def stackImages(imgArray, scale):
    rows = len(imgArray)
    cols = len(imgArray[0])
    rowsAvailable = isinstance(imgArray[0], list)
    width = imgArray[0][0].shape[1]
    height = imgArray[0][0].shape[0]
    if rowsAvailable:
        for x in range(0, rows):
            for y in range(0, cols):
                imgArray[x][y] = cv2.resize(imgArray[x][y], (0, 0), None, scale, scale)
                if len(imgArray[x][y].shape) == 2:
                    imgArray[x][y] = cv2.cvtColor(imgArray[x][y], cv2.COLOR_GRAY2BGR)
        imageBlank = np.zeros((height, width, 3), np.uint8)
        hor = [imageBlank]*rows
        hor_con =  [imageBlank]*rows
        for x in range(0, rows):
            hor[x] = np.hstack(imgArray[x])
            hor_con[x] = np.concatenate(imgArray[x])
        ver = np.vstack(hor)
        ver_con = np.concatenate(hor)
    else:
        for x in range(0, rows):
            imgArray[x] = cv2.resize(imgArray[x], (0, 0), None, scale, scale)
            if len(imgArray[x].shape) == 2:
                imgArray[x] = cv2.cvtColor(imgArray[x], cv2.COLOR_GRAY2BGR)
        hor = np.hstack(imgArray)
        hor_con = np.concatenate(imgArray)
        ver = hor
    return ver

Как видим, функция возвращает нам изображение, которое мы можем вывести следующим кодом:

imageArray = ([img, imgBlank, imgBlank, imgBlank], [imgBlank, imgBlank, imgBlank, imgBlank]) # Массив изображений
stackedImage = stackImages(imageArray, 1) # Функция, которую мы написали выше
cv2.imshow('Stacked Images', stackedImage) # Показ изображения

cv2.waitKey(0)

Интересно, что выведет весь это код? Многие функции, если что, мы написали заранее и по факту не совсем используем, но всё же они нам понадобятся в будущем. А вот что он выведет:

И это всё? Ну пока что да, но давайте всё же продолжим.

А что же у нас за imgBlank? Давайте их заменим на наше img:

imageArray = ([img, img, img, img], [img, img, img, img]) # Массив изображений

Интересный, но ожидаемый результат. Давайте продолжим!

Вернёмся к изначальному коду:

imageArray = ([img, imgBlank, imgBlank, imgBlank], [imgBlank, imgBlank, imgBlank, imgBlank]) # Массив изображений

У нас уже есть изображение, пропущенное через Treshold. Вставим его на вторую позицию:

imageArray = ([img, imgTreshold, imgBlank, imgBlank], [imgBlank, imgBlank, imgBlank, imgBlank]) # Массив изображений

И вот что получим:

Как мы видим, теперь у нас есть только контуры объектов. Это нам и нужно — нам необходимо видеть цифры и границы поля. Давайте пойдём дальше!

▍ Шаг 2. Поиск контуров

Здесь мы будем искать контуры нашего поля. Для этого напишем ещё немного букв, т. е. кода. Но для начала советую почитать про поиск контуров в OpenCV.

Теперь код (смотрите комментарии, там я постарался объяснить что происходит):

# Шаг 2. Поиск контуров
imgContours = img.copy() # Копируем изначальное изображение для преобразований
imgBigContours = img.copy() # Копируем изначальное изображение для преобразований
# Поиск контуров на изображении, пропущенном через Treshold, с помощью метода RETR_EXTERNAL
# Затем мы используем CHAIN_APPROX_SIMPLE
contours, hierarchy = cv2.findContours(imgThreshold, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[-2:]
cv2.drawContours(imgContours, contours, -1, (0, 255, 0), 3) # Рисуем все контуры, которые смогли зафиксировать

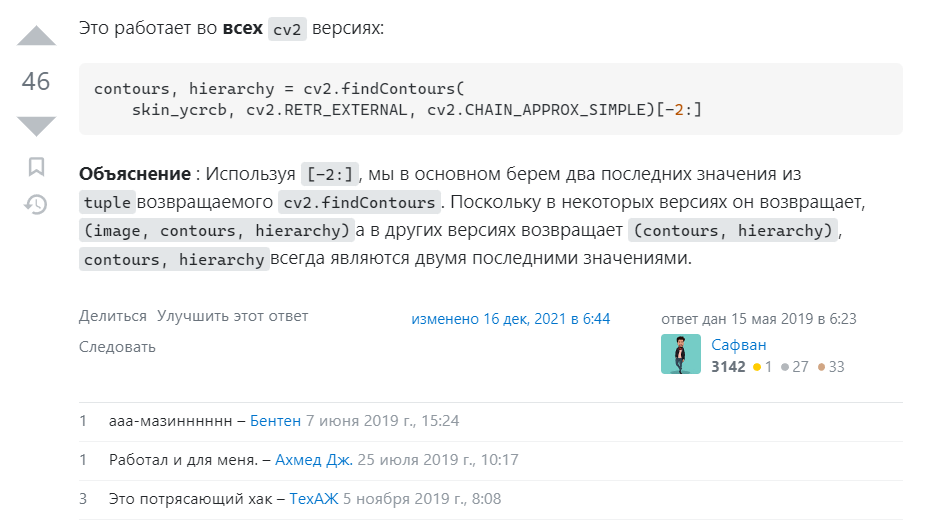
Зачем в строчке в конце стоит [-2:]:

contours, hierarchy = cv2.findContours(imgThreshold, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)[-2:]

Можно посмотреть здесь или ниже:

Теперь возьмём переменную imgContours, в которой у нас хранится изображение с обрисованными контурами, и подставим в наш вывод вместо imgBlank:

imageArray = ([img, imgThreshold, imgContours, imgBlank], [imgBlank, imgBlank, imgBlank, imgBlank]) # Массив изображений

После запуска мы получим следующую картинку с уже найденным нами контуром:

Замечание для людей, которые спросят:, а почему не отображается внутренний контур? Отвечу: потому что мы специально выделяем его, чтобы «отбросить». Это можно проиллюстрировать на следующем примерах:

Как мы видим, не всегда у нас есть «чистое изображение» для работы, поэтому мы и «отсекаем» внешние контуры. Продолжим!

▍ Шаг 3. Поиск самого большого контура и использование его в качестве поля для судоку

Для этого всего нам необходимо будет написать две функции, которые помогут нам в этом.

Функция biggestContour ():

def biggestContour(contours):
    biggest = np.array([])
    max_area = 0
    for i in contours:
        area = cv2.contourArea(i)
        if area > 50:
            peri = cv2.arcLength(i, True)
            approx = cv2.approxPolyDP(i, 0.02 * peri, True)
            if area > max_area and len(approx) == 4:
                biggest = approx
                max_area = area

    return biggest, max_area

Теперь давайте напишем функцию для переупорядочивания точек для искажения перспективы. Поясняю: мы не знаем позиции точек, которые мы получаем из переменной biggest, т. е. мы не знаем, какая точка сверху, какая снизу и т. д. Именно для понимания этого мы и напишем сейчас функцию reorder ():

def reorder(myPoints):
    myPoints = myPoints.reshape((4, 2))
    myPointsNew = np.zeros((4, 1, 2), dtype = np.int32)
    add = myPoints.sum(1)
    myPointsNew[0] = myPoints[np.argmin(add)]
    myPointsNew[3] = myPoints[np.argmax(add)]
    diff = np.diff(myPoints, axis = 1)
    myPointsNew[1] = myPoints[np.argmin(diff)]
    myPointsNew[2] = myPoints[np.argmax(diff)]
    
   return myPointsNew

Суть работы функции вы можете увидеть ниже:

Теперь запишем функцию в основном файле:

# Шаг 3. Поиск самого большого контура и использование его в качестве поля для судоку
biggest, maxArea = biggestContour(contours) # Наша самописная функция по поиску контура
if biggest.size != 0:
    biggest = reorder(biggest)
    cv2.drawContours(imgBigContours, biggest, -1, (0, 0, 255), 15) # Рисуем самый большой контур
    pts1 = np.float32(biggest)
    pts2 =np.float32([[0, 0], [widthImg, 0], [0, heightImg], [widthImg, heightImg]]) # Подготовка "точек"
    matrix = cv2.getPerspectiveTransform(pts1, pts2)
    imgWarpColored = cv2.warpPerspective(img, matrix, (widthImg, heightImg))
    imgDetectedDigits = imgBlank.copy()
    imgWarpColored = cv2.cvtColor(imgWarpColored, cv2.COLOR_BGR2GRAY)

Нам остаётся заменить imgBlank в нашем выводе на imgBigContours:

imageArray = ([img, imgThreshold, imgContours,  imgBigContours], [imgBlank, imgBlank, imgBlank, imgBlank]) # Массив изображений

И вот что мы получим:

Разберёмся с этой частью:

    imgWarpColored = cv2.warpPerspective(img, matrix, (widthImg, heightImg))
    imgDetectedDigits = imgBlank.copy()
    #imgWarpColored = cv2.cvtColor(imgWarpColored, cv2.COLOR_BGR2GRAY)

Здесь «приближаем» наше поле, и если мы закомментируем последнюю строчку, предварительно вставив переменную imgWarpColored в наш код вывода:

imageArray = ([img, imgThreshold, imgContours,  imgBigContours], [imgWarpColored, imgBlank, imgBlank, imgBlank]) # Массив изображений

Мы получим следующий результат (картинка будет в цвете):

А если раскомментируем, то получим следующие (картинка в оттенках серого):

▍ Шаг 4. Найдём на изображении каждую цифру

Для этого нам понадобится на imgWarpColored выделить каждый квадрат и предсказать там цифру (если она там есть).

Для данной задачи я обучил нейронную сеть на открытых данных MNIST. О том, как я обучал и как буду дорабатывать этот проект, я выпущу отдельную статью. Пока лишь могу показать скриншоты с кодом и получившейся точностью модели (она не сильно велика, порядка 0.7).

Сразу хочу заметить, что с распознаванием пока всё не очень хорошо, потому что я обучал на «скорую руку», сделал всего 4 эпохи обучения, вместо 10 и более, как это планировал. Блокнот в формате .ipynb вы сможете найти у меня на GitHub, на странице проекта. В дальнейшем я его обновлю, доведя модель до хорошего результата, ссылка на GitHub будет внизу. Но я надеюсь, у меня всё же получится распознать несколько цифр в этом кейсе и выдать вам минимально приемлемый результат. Ещё раз обращаю внимание, что часть с тренировкой модели распознавания цифр и интеграцией модели в проект будет в следующей статье, так как на это требуется время, а ввиду сессии у меня его нет. Прошу понять, простить и не ругаться на меня за эту ошибку.

Итак, вернёмся к коду. Нам потребуется функция splitBoxes (), чтобы разбить imgWarpColored на 81 ячейку (мы производим сплит по горизонтали и вертикали):

def splitBoxes(img):
    rows = np.vsplit(img, 9)
    boxes = []
    for r in rows:
        cols = np.hsplit(r, 9)
        for box in cols:
            boxes.append(box)
    return boxes

Давайте посмотрим, как вырезались наши ячейки. Для этого нам потребуется написать:

cv2.imshow(boxes[9])

И вот что мы получим:

Как мы видим, у нас всё вырезалось правильно и ячейка видна. Хочу заметить, что размер изображения, который мы задавали в первом шаге, должен быть кратен 9, иначе компилятор выдаст нам сообщение об ошибке:

heightImg = 450
widthImg = 450

Теперь нам нужно проинициализировать модель. Для этого мы напишем простенькую функцию загрузки модели (у меня модель называется mnist.h5):

from tensorflow.keras.models import load_model

def initializePredictionModel():
    model = load_model('mnist.h5')
    return model

Выше мы импортируем модуль «load_model» из tensorflow.keras.models (это может занять некоторое время, не пугайтесь).

Далее напишем функцию предсказания:

def getPrediciton(boxes, model):
    result = []
    for image in boxes:
        # Подготовка изображения
        img = np.asarry(image)
        img = img[4:img.shape[0] - 4, 4:img.shape[1] - 4]
        img = cv2.resize(img, (28, 28))
        img = img / 255
        img = img.reshape(1, 28, 28, 1)
        # Предсказание
        predictions = model.predict(img)
        classIndex = np.argmax(predictions, axis = -1)
        probabilityValue = np.amax(predictions)
        #print(classIndex, probabilityValue)
        # Сохранение результатов
        if probabilityValue > 0.8:
            result.append(classIndex[0])
        else:
            result.append(0)
    return result

И вот что появится в итоге:

Я экспериментировал на разных вариациях судоку, поэтому числа могут отличаться от тех скриншотов, что находятся выше. Последнее предсказание сделано на следующем варианте судоку:

Как видим из изображений выше, результаты схожи. На этом моменте я столкнулся с проблемой, о которой писал ранее, а именно проблемой с моделью, поэтому я хотел бы взять для себя время на исправление этого недостатка и на этом закончить статью. В следующей статье мы допишем наш проект по распознаванию и решению судоку в реальном времени. А пока хотел бы у вас спросить, как улучшить модель распознавания чисел? Пишите в комментариях, я обязательно прочту и мы вместе доведём этот проект до хорошего результата!

А пока все файлы, которые есть на данный момент, вы можете найти на моём GitHub.