Задачка: Сбор дождевой воды 3D
Очевидно, что каждый элемент может содержать какое-то количество воды или не содержать воды и быть частью границы одного или нескольких резервуаров с водой.
Также очевидно, что внешние элементы не могут содержать воды, так как она с них будет сливаться, а следовательно они являются границами.
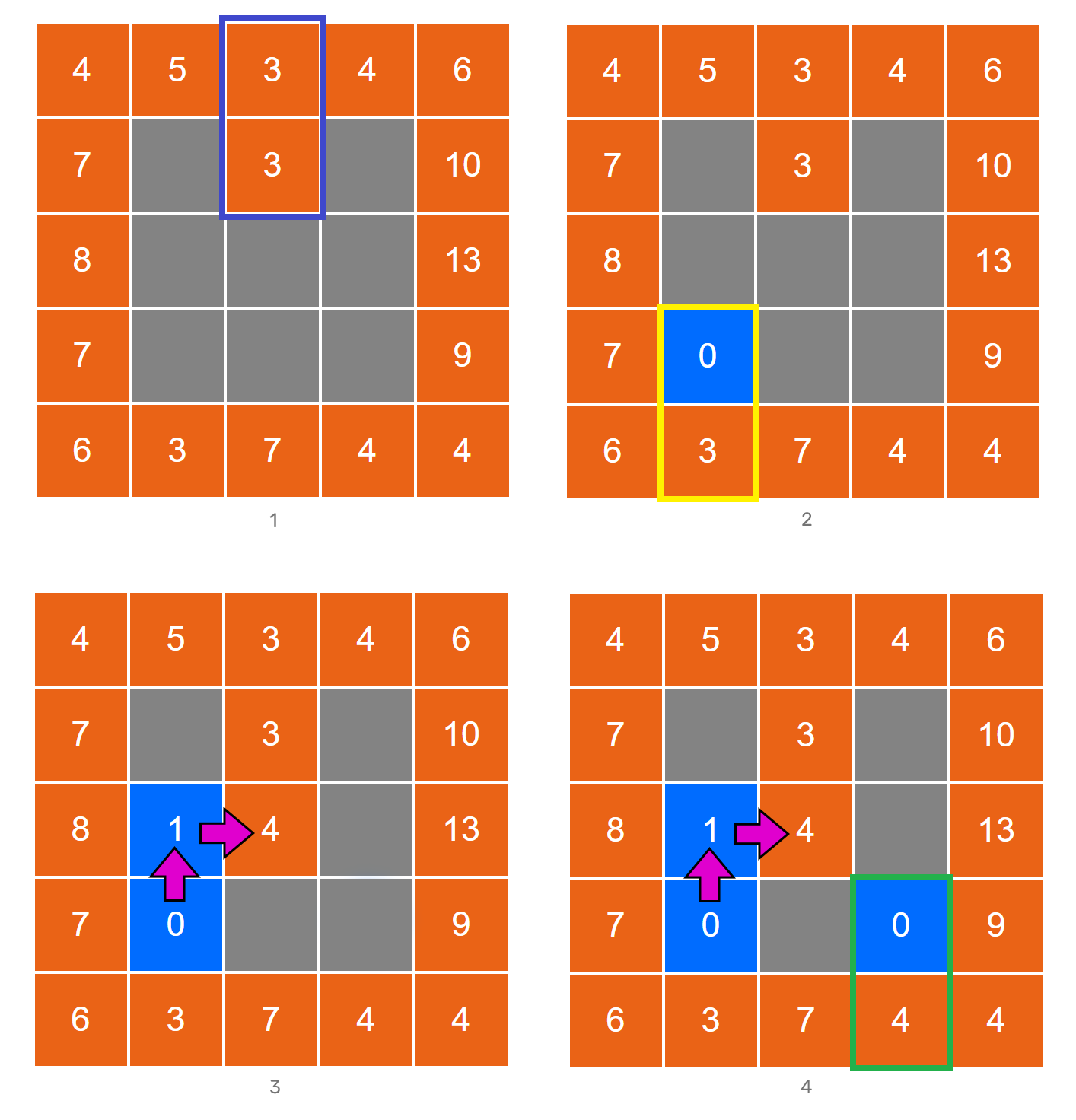
Теперь нужно понять, что если с элементом, который мы определили как границу, рядом находится элемент большей или равной высоты, то такой элемент не может содержать воды и также становится границей. (рис. 1)
Хорошо, а что мы можем сказать в ситуации, когда рядом с границей находится элемент, у которого высота меньше? Посмотрим на рис. 2, в желтом прямоугольнике у нас внешний элемент высотой 3 и рядом с ним элемент с высотой 0. Заметим, что высота 3 — это наименьшая высота из внешних элементов. Может ли в элементе 0 быть больше воды чем 3? Не может, так как она будет переливаться через рядом стоящую границу с высотой 3. А может ли в элементе 0 быть меньше воды чем 3? Тоже не может, потому что высота 3 — это наименьшая высота из внешних элементов и вода обязательно задержится каким-нибудь из них.
Продолжим обследование и пройдем один шаг вверх и один шаг направо. (рис. 3) Нам встретился элемент с высотой 1 и элемент с высотой 4. Что мы можем про них сказать? У элемента 1 уровень воды будет на уровне элемента 0, а элемент 4 будет границей. Теперь понятно, что если в процессе обследования по цепочке граничного элемента мы будем находить элементы с высотой меньше, чем у граничного то про них можно смело сказать, что они содержат воду. А если высота обследованных элементов больше или равна граничному, то такие элементы будут сами становиться границами, но мы не будем спешить с их обследованием, нам нужно еще одно рассуждение.
Пока мы обследовали элемент находящейся на внешней границе с минимальной высотой все казалось просто и логично, уровень воды определяется по высоте элемента. А как быть с остальными? Посмотрим на элемент с высотой 4. (рис. 4) Рядом с ним элемент с высотой 0 и мы уже не можем сказать уверенно сколько в нем воды. Это будет зависеть от того соединен ли этот элемент посредством элементов содержащими воду с какими-нибудь другими граничными элементами. И тут нужно понять главное — если элемент 4 соединен водой с другими границами с меньшими высотами, то вся вода на этом пути уже будет посчитана в процессе обследования меньших границ. Нам просто нужно действовать от меньших высот к большим. Если мы будем действовать таким образом, то непременно обойдем все элементы и будем знать наверняка какие элементы граничные, а какие содержат воду и уровень воды в них.
Ну вот, когда мы поняли принцип, можно начинать программировать.
Первое, что нам надо сделать это добавить все крайние элементы в очередь, упорядоченную по возрастанию высоты и отметить где-то их координаты как посещенные.
Для добавления в очередь можно написать функцию двоичного поиска. Если у нас есть, например массив чисел, то, чтобы вставить в него новое число с сохранением упорядоченности необязательно перебирать весь массив. Нужно разбить массив посередине и посмотреть в левой или правой половине продолжать поиски, а потом уже эту половину снова пополам и так далее. В худшем случае количество таких итераций будет равно логарифму числа элементов по основанию 2.
После того как мы добавили задачи начинаем их обрабатывать. Для каждой задачи запускаем волновой алгоритм. Подсчитываем воду во всех элементах меньшей высоты, а элементы большей или равной высоты добавляем в очередь с помощью нашей функции двоичного поиска. И так пока не кончатся задачи в очереди. Всё!
В процессе решения мы задействовали 3 инструмента: очередь с приоритетом, бинарный поиск и волновой алгоритм. Неплохо для одной задачки.
