Задачи реального мира: как на практике считают надежность систем (reliability, MTTF, failure rate)?
В предыдущей статье мы рассмотрели терминологию и математическую основу расчетов отказоустойчивости различных систем и выяснили, что на практике, когда речь идет об оценках MTTF (Mean Time To Failure — среднего времени до отказа) и других характеристик надежности, в большинстве случаев предполагается, что отказы подчиняются пуассоновской модели. Соответственно, их вероятностное описание основано на экспоненциальном распределении вероятностей.Этот материал будет посвящен практическим аспектам применения этой модели, причем стоит сразу оговориться, что он широко используется, как в электронике, так и в самых разных областях: например, при оценке рисков в авиационной и атомной отрасли, прогнозирования в автопроме, оценке надежности облачных сервисов в Интернете и т.п. Общим предположением, повторюсь, является гипотеза о постоянстве интенсивности отказов λ, которая, как мы увидели из предыдущей статьи, обратно пропорциональна среднему времени безотказной работы MTTF=1/λ.
Итак, давайте для начала рассмотрим совсем простой пример: устройство, состоящее из двух элементов, для каждого из которых известны интенсивности отказов λ1 и λ2. Отказ любого из элементов приводит к отказу устройства в целом. Например, компьютер (условно) можно представить, как систему, состоящую из процессора и материнской платы. Пусть для них среднее время до отказа (MTTF) равны 2 и 3 годам (соответственно, λ1=½ года-1 и λ2=⅓ года-1). Какова будет оценка MTTF для компьютера, в целом? И какова вероятность отказа компьютера через 1 год после начала эксплуатации?
Прежде всего, вспомним, что вероятность отказа каждого компонента, согласно нашей модели, Q1(t)=1-exp (-λ1t), Q2(t)=1-exp (-λ2t).Соответственно, вероятность безотказной работы компьютера, в целом: Р (t)=[ВБР компьютера]=[ВБР процессора]*[ВБР материнской платы], или, если обозначить за интенсивность отказов компьютера λ (t): exp (-λ (t)t)=exp (-λ1t)*exp (-λ2t)=exp (-(λ1+λ2)t), откудаλ (t)=λ1+λ2.Т.е. мы получили важный вывод: Интенсивность отказов системы равна сумме интенсивностей отказов ее компонент и не зависит от времени (для экспоненциального распределения, конечно).
В нашем целочисленном примере λ=½ +⅓=5/6 (лет-1), откуда MTTF=1/λ=1.2 года. Зная λ, легко вычислить вероятность отказа всего компьютера, в целом, в течение первого года: Q (t=1 год)=1-exp (-1.2)=70%, а в течение двух первых лет: Q (t=2 года)=1-exp (-2.4)=91%.
Аналогично, при помощи простого суммирования интенсивностей отказов, можно было бы посчитать MTTF системы, состоящей из большего числа компонентов.

Еще раз подчеркнем, что речь идет о, как говорят, последовательном (без резервирования) соединении элементов, при котором отказ любого из элементов приводит к отказу системы, в целом. В этом случае обычно система разбивается на сборки, для каждой из которых можно посчитать интенсивность отказов.
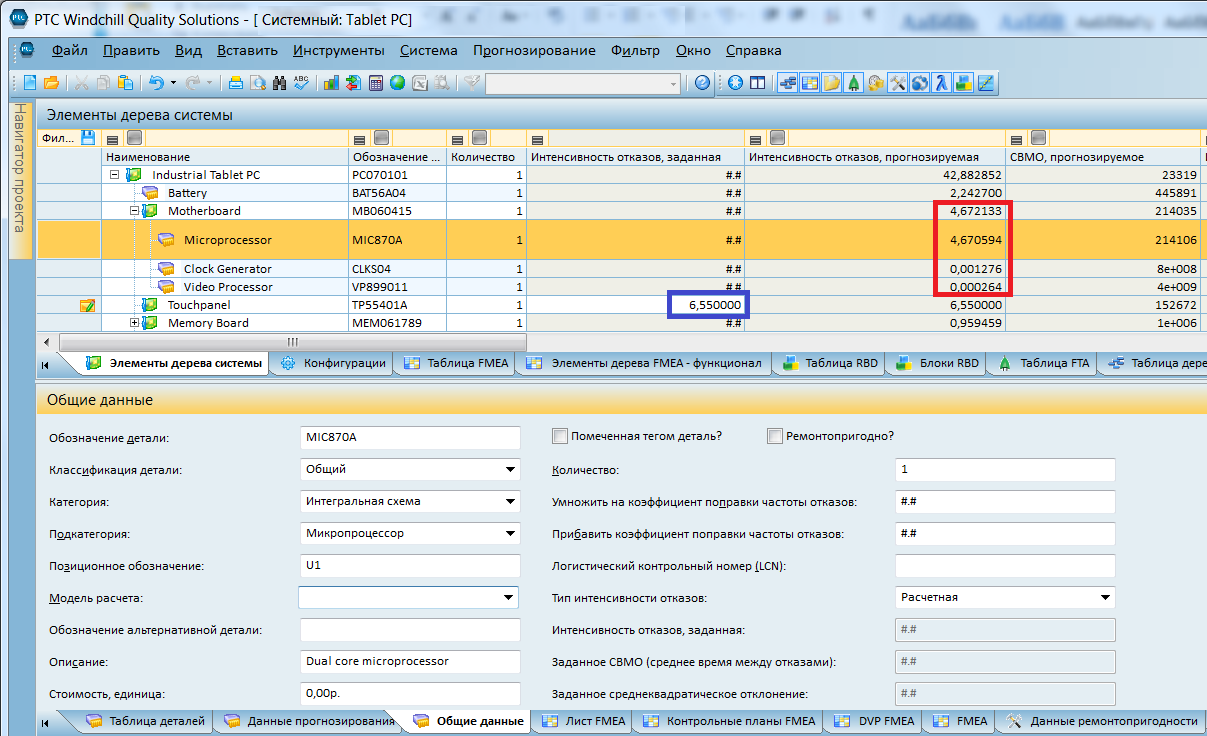
Приведенные скриншоты демонстрируют пример применения профессионального ПО для расчета надежности и рисков Windchill Quality Solutions (Relex). В практике, типичны две ситуации:
для компонентов имеется известное значение MTTF, например, указанное в паспорте (выделено синей рамкой)
MTTF компонента неизвестно — тогда приходится брать его оценку, исходя из классификаторов и справочников (красная рамка на скриншоте)
Еще один важный момент заключается в зависимости λ-характеристик от условий эксплуатации (нагрев, радиационное облучение, давление и т.д.). В частности, для электронных компонент интенсивность отказов увеличивается с ростом температуры. Данные по надежности компонентов регламентируются стандартами, различными для разных государств и отраслей экономики. Обычно эта информация собирается в справочниках и представляется в виде соответствующих интерполяционных формул, например (для резисторов): 
В заключение, еще раз отмечу, что мы рассмотрели самый простой случай: постоянная интенсивность отказов и последовательная схема. В следующих статьях мы рассмотрим, как можно повысить надежность системы при помощи резервирования компонентов.
