Задача про две ёмкости для жидкости
Существует классическая задача:
Есть 2 емкости: 5 литров и 3 литра. Как отмерить 4 литра жидкости используя только эти 2 емкости?
Понятное дело что тут важно не сколько знание правильного ответа, а знание метода решения таких задач. Ведь вместо целевых 4х литров могут спросить отсчитать и 1,2,6,7 литров.
В этом тексте я решу эту задачу в общем виде при помощи конечного автомата. Так как тут явно можно проследить состояния и входные воздействия. Также я упомяну про малоизвестный язык Front-End разметки Dot. Методика конечного автомата хорошо изучена и поставлена на рельсы. Состоит из 3 фаз.
Фаза №1: перечислить все возможные состояния (комбинаторика)

Состояние определяется количеством жидкости в паре сосудов. Согласно комбинаторике по правилу умножения существует всего 24 состояния. Вот они все перечислены.
Фаза №2 перечислить все возможные входы. (из условий задачи)
Существует всего 5 легальных действий с бутылками. Вот их перечень.
 №
№
Фаза №3 составить таблицу переходов
Этот пункт я пропущу так как таблица получится циклопических размеров. По правилу умножения 24×5=120 переходов
Фаза №4 отрисовать граф состояний (Helicopter view)
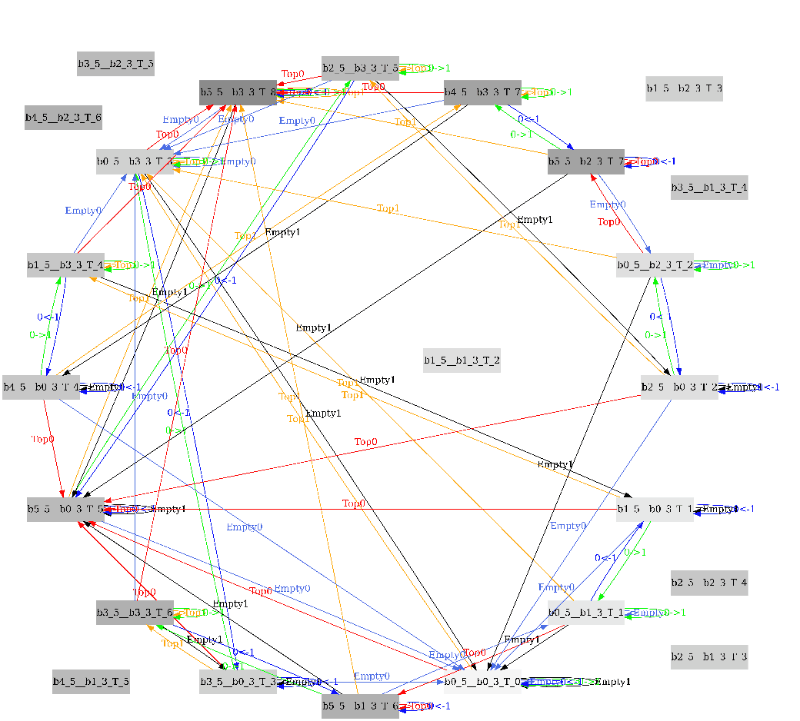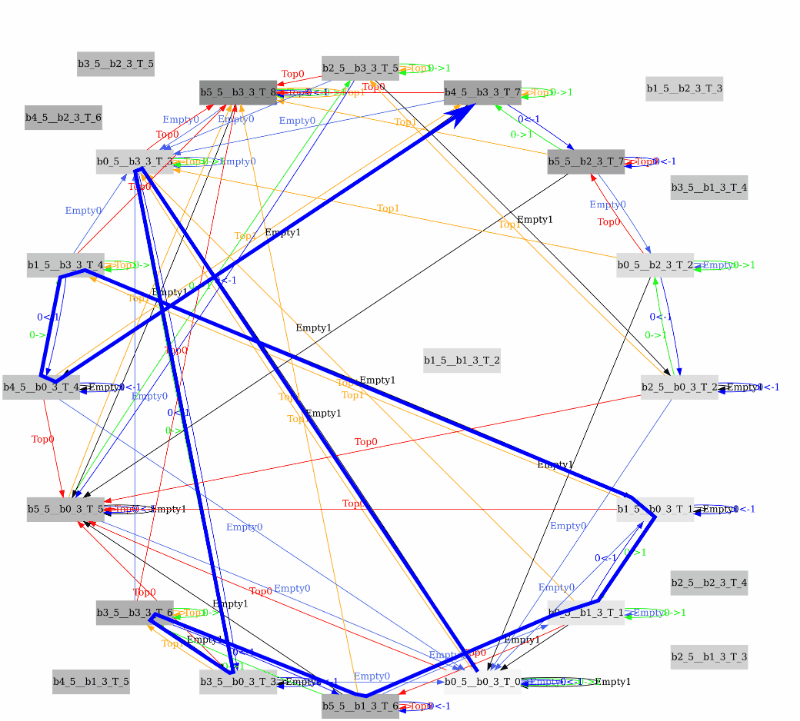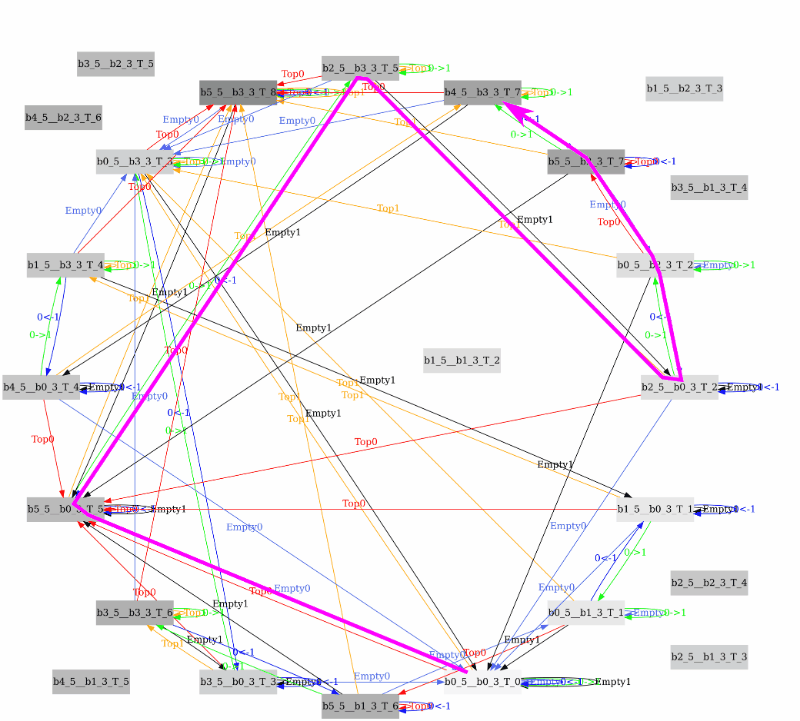
Как гласит английская народная пословица »Картинка стоит тысячи слов» (A picture is worth a thousand words). Также мой универский профессор часто говорил, что инженеры — это про схемы. Поэтому представляю блок-схему в виде ориентированного графа состояний для задачи про бутылки.

Я накропал на языке С консольную утилиту, которая прокручивает конечный автомат и сохраняет в файл составленный код на языке dot. Далее бесплатная утилита dot.exe поедает файл *.dot и преобразует его во всем известный *.svg файл. Наконец браузер Chrome.exe поедает *.svg и отрисовывает в окне на мониторе. Язык Dot хорош тем что он имеет простой синтаксис. Dot более высокоуровневый язык, чем спецификация *.svg файлов.
Глядя на этот ориентированный граф становится очевидным, что чтобы отмерить 4 литра надо выполнить следующую процедуру из 6-ти инструкций:
 возможные действия с бутылками
возможные действия с бутылками
есть еще одно синее решение
Easy!
Вот код Dot графа для тех, кто захочет изучить граф внимательнее.
digraph G {
b0_5__b0_3_T_0 [label="b0_5__b0_3_T_0" color=grey96 style=filled shape=box];
b0_5__b0_3_T_0->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b5_5__b0_3_T_5 [label="b5_5__b0_3_T_5" color=grey73 style=filled shape=box];
b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b5_5__b0_3_T_5->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
b5_5__b3_3_T_8 [label="b5_5__b3_3_T_8" color=grey55 style=filled shape=box];
b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
b5_5__b3_3_T_8->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b3_3_T_3 [label="b0_5__b3_3_T_3" color=grey82 style=filled shape=box];
b0_5__b3_3_T_3->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b3_3_T_3->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
b0_5__b3_3_T_3->b0_5__b3_3_T_3 [label="0->1" color=green fontcolor=green]
b0_5__b3_3_T_3->b3_5__b0_3_T_3 [label="0<-1" color=blue fontcolor=blue]
b3_5__b0_3_T_3 [label="b3_5__b0_3_T_3" color=grey82 style=filled shape=box];
b3_5__b0_3_T_3->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b3_5__b0_3_T_3->b3_5__b3_3_T_6 [label="Top1" color=orange fontcolor=orange]
b3_5__b3_3_T_6 [label="b3_5__b3_3_T_6" color=grey69 style=filled shape=box];
b3_5__b3_3_T_6->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b3_5__b3_3_T_6->b3_5__b3_3_T_6 [label="Top1" color=orange fontcolor=orange]
b3_5__b3_3_T_6->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b3_5__b3_3_T_6->b3_5__b0_3_T_3 [label="Empty1" color=aqua fontcolor=aqua]
b3_5__b3_3_T_6->b3_5__b3_3_T_6 [label="0->1" color=green fontcolor=green]
b3_5__b3_3_T_6->b5_5__b1_3_T_6 [label="0<-1" color=blue fontcolor=blue]
b5_5__b1_3_T_6 [label="b5_5__b1_3_T_6" color=grey69 style=filled shape=box];
b5_5__b1_3_T_6->b5_5__b1_3_T_6 [label="Top0" color=Red fontcolor=Red]
b5_5__b1_3_T_6->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
b5_5__b1_3_T_6->b0_5__b1_3_T_1 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b1_3_T_1 [label="b0_5__b1_3_T_1" color=grey91 style=filled shape=box];
b0_5__b1_3_T_1->b5_5__b1_3_T_6 [label="Top0" color=Red fontcolor=Red]
b0_5__b1_3_T_1->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
b0_5__b1_3_T_1->b0_5__b1_3_T_1 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b1_3_T_1->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
b0_5__b1_3_T_1->b0_5__b1_3_T_1 [label="0->1" color=green fontcolor=green]
b0_5__b1_3_T_1->b1_5__b0_3_T_1 [label="0<-1" color=blue fontcolor=blue]
b1_5__b0_3_T_1 [label="b1_5__b0_3_T_1" color=grey91 style=filled shape=box];
b1_5__b0_3_T_1->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b1_5__b0_3_T_1->b1_5__b3_3_T_4 [label="Top1" color=orange fontcolor=orange]
b1_5__b3_3_T_4 [label="b1_5__b3_3_T_4" color=grey78 style=filled shape=box];
b1_5__b3_3_T_4->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b1_5__b3_3_T_4->b1_5__b3_3_T_4 [label="Top1" color=orange fontcolor=orange]
b1_5__b3_3_T_4->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b1_5__b3_3_T_4->b1_5__b0_3_T_1 [label="Empty1" color=aqua fontcolor=aqua]
b1_5__b3_3_T_4->b1_5__b3_3_T_4 [label="0->1" color=green fontcolor=green]
b1_5__b3_3_T_4->b4_5__b0_3_T_4 [label="0<-1" color=blue fontcolor=blue]
b4_5__b0_3_T_4 [label="b4_5__b0_3_T_4" color=grey78 style=filled shape=box];
b4_5__b0_3_T_4->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b4_5__b0_3_T_4->b4_5__b3_3_T_7 [label="Top1" color=orange fontcolor=orange]
b4_5__b3_3_T_7 [label="b4_5__b3_3_T_7" color=grey64 style=filled shape=box];
b4_5__b3_3_T_7->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b4_5__b3_3_T_7->b4_5__b3_3_T_7 [label="Top1" color=orange fontcolor=orange]
b4_5__b3_3_T_7->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b4_5__b3_3_T_7->b4_5__b0_3_T_4 [label="Empty1" color=aqua fontcolor=aqua]
b4_5__b3_3_T_7->b4_5__b3_3_T_7 [label="0->1" color=green fontcolor=green]
b4_5__b3_3_T_7->b5_5__b2_3_T_7 [label="0<-1" color=blue fontcolor=blue]
b5_5__b2_3_T_7 [label="b5_5__b2_3_T_7" color=grey64 style=filled shape=box];
b5_5__b2_3_T_7->b5_5__b2_3_T_7 [label="Top0" color=Red fontcolor=Red]
b5_5__b2_3_T_7->b5_5__b3_3_T_8 [label="Top1" color=orange fontcolor=orange]
b5_5__b2_3_T_7->b0_5__b2_3_T_2 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b2_3_T_2 [label="b0_5__b2_3_T_2" color=grey87 style=filled shape=box];
b0_5__b2_3_T_2->b5_5__b2_3_T_7 [label="Top0" color=Red fontcolor=Red]
b0_5__b2_3_T_2->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
b0_5__b2_3_T_2->b0_5__b2_3_T_2 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b2_3_T_2->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
b0_5__b2_3_T_2->b0_5__b2_3_T_2 [label="0->1" color=green fontcolor=green]
b0_5__b2_3_T_2->b2_5__b0_3_T_2 [label="0<-1" color=blue fontcolor=blue]
b2_5__b0_3_T_2 [label="b2_5__b0_3_T_2" color=grey87 style=filled shape=box];
b2_5__b0_3_T_2->b5_5__b0_3_T_5 [label="Top0" color=Red fontcolor=Red]
b2_5__b0_3_T_2->b2_5__b3_3_T_5 [label="Top1" color=orange fontcolor=orange]
b2_5__b3_3_T_5 [label="b2_5__b3_3_T_5" color=grey73 style=filled shape=box];
b2_5__b3_3_T_5->b5_5__b3_3_T_8 [label="Top0" color=Red fontcolor=Red]
b2_5__b3_3_T_5->b2_5__b3_3_T_5 [label="Top1" color=orange fontcolor=orange]
b2_5__b3_3_T_5->b0_5__b3_3_T_3 [label="Empty0" color=royalblue fontcolor=royalblue]
b2_5__b3_3_T_5->b2_5__b0_3_T_2 [label="Empty1" color=aqua fontcolor=aqua]
b2_5__b3_3_T_5->b2_5__b3_3_T_5 [label="0->1" color=green fontcolor=green]
b2_5__b3_3_T_5->b5_5__b0_3_T_5 [label="0<-1" color=blue fontcolor=blue]
b2_5__b0_3_T_2->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b2_5__b0_3_T_2->b2_5__b0_3_T_2 [label="Empty1" color=aqua fontcolor=aqua]
b2_5__b0_3_T_2->b0_5__b2_3_T_2 [label="0->1" color=green fontcolor=green]
b2_5__b0_3_T_2->b2_5__b0_3_T_2 [label="0<-1" color=blue fontcolor=blue]
b5_5__b2_3_T_7->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
b5_5__b2_3_T_7->b4_5__b3_3_T_7 [label="0->1" color=green fontcolor=green]
b5_5__b2_3_T_7->b5_5__b2_3_T_7 [label="0<-1" color=blue fontcolor=blue]
b4_5__b0_3_T_4->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b4_5__b0_3_T_4->b4_5__b0_3_T_4 [label="Empty1" color=aqua fontcolor=aqua]
b4_5__b0_3_T_4->b1_5__b3_3_T_4 [label="0->1" color=green fontcolor=green]
b4_5__b0_3_T_4->b4_5__b0_3_T_4 [label="0<-1" color=blue fontcolor=blue]
b1_5__b0_3_T_1->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b1_5__b0_3_T_1->b1_5__b0_3_T_1 [label="Empty1" color=aqua fontcolor=aqua]
b1_5__b0_3_T_1->b0_5__b1_3_T_1 [label="0->1" color=green fontcolor=green]
b1_5__b0_3_T_1->b1_5__b0_3_T_1 [label="0<-1" color=blue fontcolor=blue]
b5_5__b1_3_T_6->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
b5_5__b1_3_T_6->b3_5__b3_3_T_6 [label="0->1" color=green fontcolor=green]
b5_5__b1_3_T_6->b5_5__b1_3_T_6 [label="0<-1" color=blue fontcolor=blue]
b3_5__b0_3_T_3->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b3_5__b0_3_T_3->b3_5__b0_3_T_3 [label="Empty1" color=aqua fontcolor=aqua]
b3_5__b0_3_T_3->b0_5__b3_3_T_3 [label="0->1" color=green fontcolor=green]
b3_5__b0_3_T_3->b3_5__b0_3_T_3 [label="0<-1" color=blue fontcolor=blue]
b5_5__b3_3_T_8->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="0->1" color=green fontcolor=green]
b5_5__b3_3_T_8->b5_5__b3_3_T_8 [label="0<-1" color=blue fontcolor=blue]
b5_5__b0_3_T_5->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="Empty1" color=aqua fontcolor=aqua]
b5_5__b0_3_T_5->b2_5__b3_3_T_5 [label="0->1" color=green fontcolor=green]
b5_5__b0_3_T_5->b5_5__b0_3_T_5 [label="0<-1" color=blue fontcolor=blue]
b0_5__b0_3_T_0->b0_5__b3_3_T_3 [label="Top1" color=orange fontcolor=orange]
b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="Empty0" color=royalblue fontcolor=royalblue]
b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="Empty1" color=aqua fontcolor=aqua]
b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="0->1" color=green fontcolor=green]
b0_5__b0_3_T_0->b0_5__b0_3_T_0 [label="0<-1" color=blue fontcolor=blue]
b1_5__b1_3_T_2 [label="b1_5__b1_3_T_2" color=grey87 style=filled shape=box];
b1_5__b2_3_T_3 [label="b1_5__b2_3_T_3" color=grey82 style=filled shape=box];
b2_5__b1_3_T_3 [label="b2_5__b1_3_T_3" color=grey82 style=filled shape=box];
b2_5__b2_3_T_4 [label="b2_5__b2_3_T_4" color=grey78 style=filled shape=box];
b3_5__b1_3_T_4 [label="b3_5__b1_3_T_4" color=grey78 style=filled shape=box];
b3_5__b2_3_T_5 [label="b3_5__b2_3_T_5" color=grey73 style=filled shape=box];
b4_5__b1_3_T_5 [label="b4_5__b1_3_T_5" color=grey73 style=filled shape=box];
b4_5__b2_3_T_6 [label="b4_5__b2_3_T_6" color=grey69 style=filled shape=box];
}Можно отрисовать граф на этом сайте и сохранить его в *.svg.
Редактировать *.svg можно при помощи бесплатной программы Inkscape.exe.
Эта задача может служить отличной иллюстрацией для обучения теории конечных автоматов FSM. Конечные автоматы повсеместно используются в промышленной разработке, например, системного программного обеспечения.
Существует 8 недостижимых состояний: 1/5_1/3; 1/5_2/3; 2/5_1/3; 2/5_2/3; 3/5_1/3; 3/5_2/3; 4/5_1/3; 4/5+2/3. В эти состояния никак не попасть как только не переливай содержимое сосудов. Если вы захотите завалить человека на собеседовании, то можно попросить его «как перелить жидкости так чтобы в каждой бутылине осталось по 2 литра?» или «как перелить жидкости так чтобы в каждой бутылке осталось по 1 литру?».
Формально можно отмерить не только 4 лита, а все значения от 1 до 8 включительно.
Вывод
Как видите, язык Front-End разметки Dot отлично подходит для автоматической отрисовки сложной векторной графики. Конечно dot тула несовершенна и даже планарные графы строит с пересечениями ребер. Если вы знаете тулу которая гарантирует планарность, то укажите это в комментариях.
Буду признателен, если пришлете описания подобного рода логических задач в комментариях к тексту.
