Задача коммивояжера (TSP) точное решение — метод целочисленного линейного программирования (Integer programming)

Все пути одинаковы: они ведут в никуда. Но у одних есть сердце, а у других — нет. Один путь дает тебе силы, другой — уничтожает тебя.
— Карлос Кастанеда
Здравствуйте уважаемые дамы и господа, а также не бинарные личности. Хорошей эпохи.
Мы с вами уже пробовали решать точно задачу коммивояжёра методом динамического программирования и методом ветвей и границ, результат не плох, но слабоват.
В данной статье постараюсь показать, что точное решение ближе, чем принято считать.
Мы будем использовать метод целочисленного программирования, который является частным случаем линейного программирования, который в свою очередь является подклассом математического программирования.
Математическое программирование — это область математики, разрабатывающая теорию, численные методы решения многомерных задач оптимизации с ограничениями.
Ограничения могут быть:
дискретными (дискретное программирование или комбинаторная оптимизация (метод динамического программирования, ветвей и границ можно отнести сюда))
линейными (целочисленными или непрерывными)
нелинейными
Но и сама целевая функция может быть:
линейной (Linear programming, LP)
квадратичной (Quadratic programming, QP)
другой нелинейной (Conic optimization, др.)
В данной работе нас будет интересовать линейное программирование, где целевая функция и ограничения выражены линейно.
В свою очередь от того какой тип переменных используется, можно выделить:
Булево программирование (Binary integer programming, PIB)
Целочисленное (все переменные целочисленные, Integer programming, IP)
Смешанное (часть переменных целочисленная, Mixed-integer programming, MIP)
Линейное (все переменные рассматриваются как не целые, непрерывные — continuous, LP)
Для каждого класса задач есть свои методы, часть пересекается, часть имеет свои границы применения. Я не буду заострять ваше внимание на этом. Меня в первую очередь интересует прикладная применимость в работе.
Поэтому, если все сильно упростить, то можно сделать вывод: чем более непрерывны переменные, тем легче найти решение (Linear programming легче находит решение, чем Mixed-integer и Integer programming)
Но так как в нашей жизни многие процессы дискретны (например, трудно представить покупку 1,25 автомобиля, или разбить 0,5 яйца), на практике применяется метод релаксации (аппроксимация сложной проблемы соседней проблемой, которую легче решить).
То есть, задача решается как не целочисленная (или не бинарная), а затем к полученным данным применяются дополнительные ограничения, которые приводят задачу к желаемому результату.
Прежде чем мы перейдём непосредственно к алгоритму, скажем пару слов за инструментарий.
Решать задачу я предлагаю на языке Python, как очень удобном средстве прототипирования и проектирования с большим набором внешних библиотек расширения.
Для наших целей кроме основного набора модулей нам понадобится решатель (solver) задач целочисленного (IP) или смешанного программирования (MIP). Подойдёт любой корректный решатель.
В своих изысканиях я опробовал три библиотеки содержащих решатели IP/MIP: PuLP, CVXPY и SciPy.
PuLP — даже из названия становится понятно, что это библиотека, которая предназначена для решения задач линейного программирования. Среди иных альтернатив она выделяется минимализмом, проста для освоения новичками, отличается удобством использования и возможностью подключать внешние решатели.
CVXPY — это встроенный в Python язык моделирования с открытым исходным кодом для задач выпуклой оптимизации. В отличие от PuLP, может решать не только линейные задачи. Содержит более богатый функционал и приличный набор подключаемых решателей. Однако, как мне показалось CVXPY справляется с однотипными задачами медленнее, чем PuLP на тех же внешних решателях (по крайней мере, MIP) и более сложен для изучения. Если вам не требуется для работы выпуклая целевая функция, то я бы его для данной задачи не рекомендовал.
SciPy — библиотека для языка программирования Python с открытым исходным кодом, предназначенная для выполнения научных и инженерных расчётов. Нас интересует её модуль optimize — средства оптимизации. Скажу сразу, это весьма сложный подход, но среди всех опенсорсных решений самый быстрый, что я нашёл.
В примерах к статье буду приводить примеры в основном с использованием PuLP, чтобы вам легче было разобраться.
Ниже будут рассмотрены существующие решатели только целочисленных и смешанных линейных уравнений, применимых для наших целей.
Сначала установим сам PuLP он собирается со встроенным решателем CBC от COIN-OR Foundation, имеет неплохую производительность.
pip install pulpSCIP — так же свободный решатель, но для данной задачи он меня несколько разочаровал. Это не означает что решатель плох, как по мне он уступает CBC в скорости.
CPLEX — классный коммерческий решатель от IBM. Существует комьюнити версия не для коммерческого использования, которая может решать линейные уравнения до 1000 переменных и 1000 ограничений (для задачи коммивояжера матрицы n<=45)
pip install cplex docplexGUROBI — ещё один замечательный коммерческий решатель. Существует комьюнити версия не для коммерческого использования, которая может решать линейные уравнения до 2000 переменных (для задачи коммивояжера матрицы n<=63)
pip install gurobipyXpress — так же хороший проприетарный решатель.
Комьюнити версия не для коммерческого использования, может решать линейные уравнения до 5000 переменных + ограничений (для задачи коммивояжера матрицы ~n<=98)
pip install xpressЗдесь не просто так приведены ссылки на коммерческие решатели, так как они справляются с той же задачей в несколько раз быстрее на одинаковом наборе данных. У CPLEX и GUROBI есть возможность скачать бесплатную академическую лицензию. Так как я не являюсь участником университетской деятельности, мне этот путь заказан, но согласитесь, подход компаний подкупает, пока не посмотришь на коммерческие ценники.
Перейдём к самому алгоритму.
Шаг
Возьмём симметричную матрицу смежности для некого графа на 5 вершин:
[[ 0 14 3 13 8]
[14 0 16 2 7]
[ 3 16 0 14 10]
[13 2 14 0 6]
[ 8 7 10 6 0]]Найдём для неё минимальный Гамильтонов цикл используя PuLP.
import pulp as pl
# Создадим модель задачи для решения - минимизировать длину пути
model = pl.LpProblem(name="tsp", sense=pl.LpMinimize)
# Подключаем решатель
solver = pl.PULP_CBC_CMD(msg=False)
# Заводим массив переменных
x = [pl.LpVariable(name=f'x_{i:02}_{j:02}', cat='Binary') for i in range(n) for j in range(n)]
# Устанавливаем целевую функцию
model += pl.lpSum([matrix[i][j] * x[i * n + j if i < j else j * n + i] for i in range(n) for j in range(n) if i < j])
# Вносим ограничения модели
for i in range(n):
model += pl.lpSum([x[i * n + j if i < j else j * n + i] for j in range(n) if i != j]) == 2Если сейчас вывести модель, то она будет выглядеть так:
tsp:
MINIMIZE
14*x_00_01 + 3*x_00_02 + 13*x_00_03 + 8*x_00_04 + 16*x_01_02 + 2*x_01_03 + 7*x_01_04 + 14*x_02_03 + 10*x_02_04 + 6*x_03_04 + 0
SUBJECT TO
_C1: x_00_01 + x_00_02 + x_00_03 + x_00_04 = 2
_C2: x_00_01 + x_01_02 + x_01_03 + x_01_04 = 2
_C3: x_00_02 + x_01_02 + x_02_03 + x_02_04 = 2
_C4: x_00_03 + x_01_03 + x_02_03 + x_03_04 = 2
_C5: x_00_04 + x_01_04 + x_02_04 + x_03_04 = 2
VARIABLES
0 <= x_00_01 <= 1 Integer
0 <= x_00_02 <= 1 Integer
0 <= x_00_03 <= 1 Integer
0 <= x_00_04 <= 1 Integer
0 <= x_01_02 <= 1 Integer
0 <= x_01_03 <= 1 Integer
0 <= x_01_04 <= 1 Integer
0 <= x_02_03 <= 1 Integer
0 <= x_02_04 <= 1 Integer
0 <= x_03_04 <= 1 Integerx_[i]_[j] — это переменная которая отвечает за то, выбирается данное ребро или нет (1 / 0).
14 * x_[i]_[j] — это вес ребра из матрицы смежности.
Ограничения говорят нам о том, что в каждую вершину должно вести ровно два пути, по одному мы приходим в вершину, а по-другому можем выйти.
Запустив решатель
status = model.solve(solver)
for v in model.variables():
print(f'{v.name} = {round(v.value())}')
print(f'Minimum path = {round(model.objective.value())}')получим:
x_00_01 = 0
x_00_02 = 1
x_00_03 = 0
x_00_04 = 1
x_01_02 = 0
x_01_03 = 1
x_01_04 = 1
x_02_03 = 1
x_02_04 = 0
x_03_04 = 0
Minimum path = 34Нам остаётся только отобразить на графе данные рёбра.
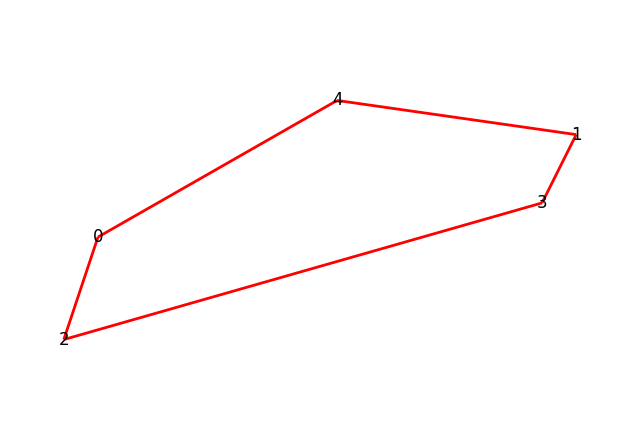
Мы нашли Гамильтонов цикл минимальной длины.
Шаг
Возьмём матрицу крупнее и проведём те же действия
[[ 0 5 8 5 7 1]
[ 5 0 12 4 4 5]
[ 8 12 0 13 15 7]
[ 5 4 13 0 2 6]
[ 7 4 15 2 0 8]
[ 1 5 7 6 8 0]]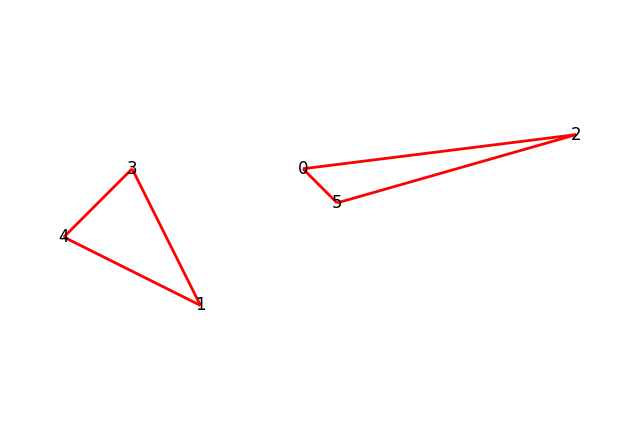
О нет, что-то пошло не так!
Minimum path = 26Мы нашли минимальный путь, проходящий через все вершины, но вот граф распался на два множества, так дело не пойдёт.
Как мы понимаем, что решение не верное? У нас есть верный признак: если множество распадается на два или более подмножества, значит это неверное решение.
В модуле networkx есть масса всяческих полезных алгоритмов для работы с графами на все случаи жизни.
Нас будет интересовать функция nx.connected_components, которая возвращает генератор для графа в виде набора множеств, из которого он состоит.
print(list(nx.connected_components(graph))[{0, 2, 5}, {1, 3, 4}]Нам нужно ввести дискриминирующую функцию, которая бы отвергала решение в случае, если оно распадается на множества. Мы поступим следующим образом: если в графе больше одного множества, то мы откажемся от такого решения и добавим новое ограничение. Ограничение должно быть таким, что бы мешало сформировать ошибочное решение повторно.
model += pl.lpSum([x[i[0] * n + i[1] if i[0] < i[1] else i[1] * n + i[0]] for i in graph.edges]) <= n - 2В модели сформировалось новое условие:
_C7: x_00_02 + x_00_05 + x_01_03 + x_01_04 + x_02_05 + x_03_04 <= 4Запускаем решатель ещё раз, с уточнёнными ограничениями.
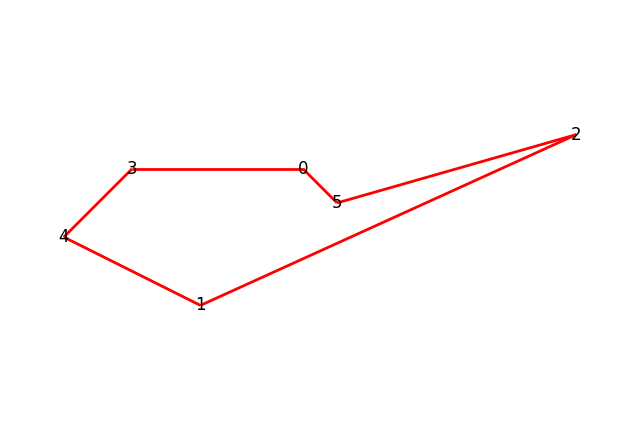
Minimum path = 31Путь стал немного длиннее чем ранее, но зато решение верно.
Шаг
Для графов большей размерности мы можем проворачивать подобный трюк в цикле до тех пор, пока решение не будет найдено.
Однако даже для такого не серьёзного графа, как этот, n=13:
[[ 0 35 87 67 77 63 51 118 121 132 116 9 92]
[ 35 0 52 58 45 30 21 91 109 118 107 44 73]
[ 87 52 0 71 20 39 39 57 98 103 104 97 61]
[ 67 58 71 0 51 80 44 63 54 65 50 74 30]
[ 77 45 20 51 0 45 26 48 81 87 85 86 42]
[ 63 30 39 80 45 0 36 92 123 131 125 71 85]
[ 51 21 39 44 26 36 0 70 90 99 90 60 53]
[118 91 57 63 48 92 70 0 54 53 64 127 33]
[121 109 98 54 81 123 90 54 0 12 13 128 38]
[132 118 103 65 87 131 99 53 12 0 24 140 46]
[116 107 104 50 85 125 90 64 13 24 0 122 43]
[ 9 44 97 74 86 71 60 127 128 140 122 0 100]
[ 92 73 61 30 42 85 53 33 38 46 43 100 0]]Алгоритму потребовалось пройти 208 шагов и добавить 207 дополнительных ограничений, к тому же расчёт затянулся на несколько минут.
Так как с ростом размера входной матрицы количество множеств, на которое может распасться решение возрастает экспоненциально. Нам нужна другая стратегия!
Шаг
Утверждаю, что аналогичного решения можно добиться всего за 4 шага решателя и добавив всего 6 ограничений. Всё что нужно было сделать, это изменить набор ограничивающих условий.
Дискриминирующая функция должна создать такие условия, что бы препятствовали распаду графа на отдельные множества.
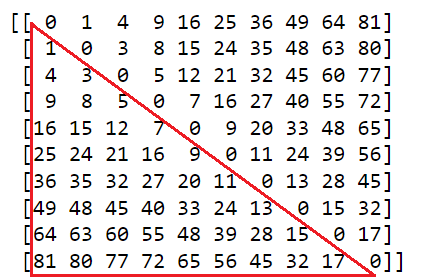
Вот одно из ограничений:
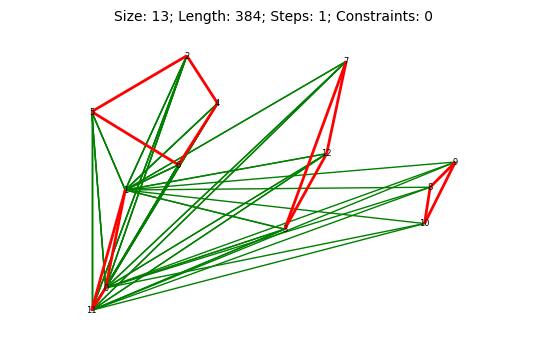 В данном изображении содержится ключ к предложенному методу
В данном изображении содержится ключ к предложенному методу
Зелёным обозначены рёбра которые попадают в неравенство
_C14: x_00_02 + x_00_03 + x_00_04 + x_00_05 + x_00_06 + x_00_07 + x_00_08
+ x_00_09 + x_00_10 + x_00_12 + x_01_02 + x_01_03 + x_01_04 + x_01_05
+ x_01_06 + x_01_07 + x_01_08 + x_01_09 + x_01_10 + x_01_12 + x_02_11
+ x_03_11 + x_04_11 + x_05_11 + x_06_11 + x_07_11 + x_08_11 + x_09_11
+ x_10_11 + x_11_12 >= 2Такое ограничение нужно выделить для каждого подграфа. На первом этапе в этом примере их должно быть четыре.
Это очень похоже на то, как если бы мы взяли липкую ленту и перемотали граф в тех местах, где он пытается развалиться. Такой простой подход позволяет, нет, не в разы, а на порядки уменьшить число вычислений (для больших матриц).
Внимание! Суть метода:
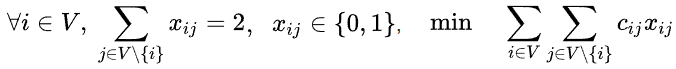
Следующее ограничение мне сложно выразить математически, но звучать оно должно следующим образом:
Для каждого подмножества, на которые распадалось множество V на предыдущих этапах, должно существовать по крайней мере две связи, соединяющие его с другими подмножествами соответствующего этапа.
Процесс поиска повторять до тех пор, пока не останется только одно множество, оно и будет искомым.

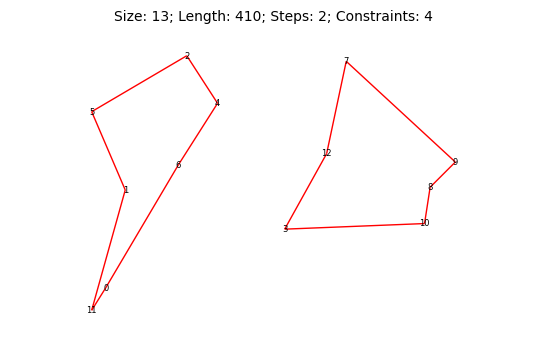
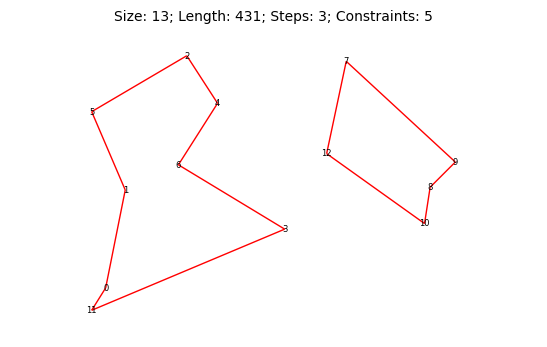
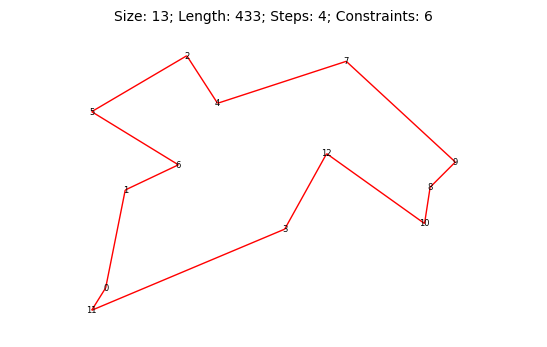
По моим выкладкам получается, что даже в самом худшем случае алгоритму на симметричном полносвязном графе необходимо не больше чем шагов:
и не больше чем дополнительных ограничений:
Число 6 в сумме не случайно, на графах с числом вершин пять и менее дополнительные ограничения совсем не нужны, так как в таком случае не могут появится подциклы. (Для образования подцикла при текущей формулировке задачи требуется минимум три вершины.)
Так для n = 100, нужно не более 523, дополнительных ограничений в худшем случае, а для n=1000, 19613, что вполне не плохо.
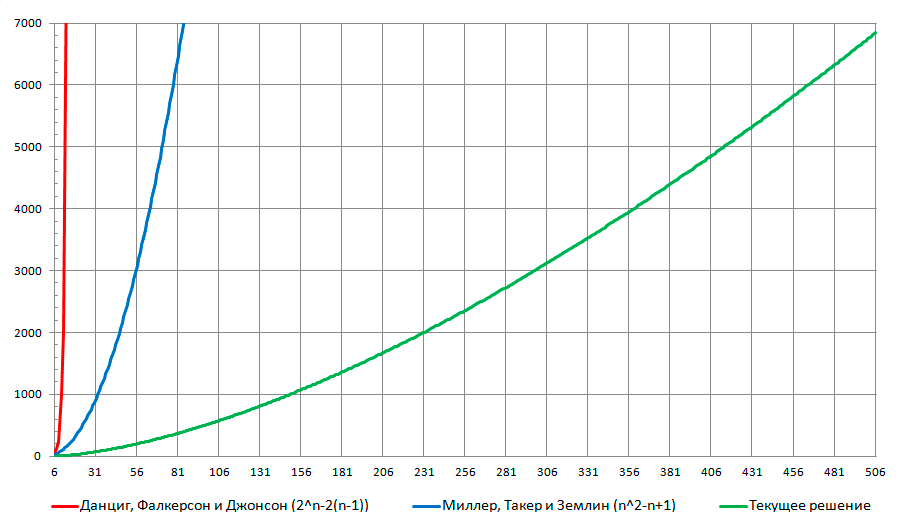 Зависимость количества дополнительных ограничений от размера входной матрицы в худшем случае.
Зависимость количества дополнительных ограничений от размера входной матрицы в худшем случае.
Исходя из того, что исходные условие задаются симметричной матрицей смежности, мы можем для экономии памяти отбросить верхнюю или нижнюю её часть, а также главную диагональ.
Уменьшим, таким образом, число переменных для солвера до:
Почему же так важно уменьшить число переменных и дополнительных ограничений? Если под капотом у решателя находится симплекс метод, или его аналог, то формируется матрица:
Здача коммивояжёра на максимум
Имея решение замкнутой задачи не столь сложно немного изменить условие и сделать не замкнутый вариант.
 Здача коммивояжёра не замкнутый вариант решения
Здача коммивояжёра не замкнутый вариант решения
Не убедил, что решение торт? Тестируйте!
TSP PuLP
#------------------------------------------------------------------------------------
# TSP_ILP - traveling salesman problem integer linear programming (ILP) method
# Решатель задачи комивояжора методом целочисленного линейного программирования
# Rebuilder 21.01.2023 https://habr.com/ru/publication/edit/711708/
#------------------------------------------------------------------------------------
import numpy as np
import random
import matplotlib.pyplot as plt
import networkx as nx
import pulp as pl
from datetime import datetime
#------------------------------------------------------------------------------------
def distance(x1, y1, x2, y2):
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#------------------------------------------------------------------------------------
print('Подключенные решатели:', pl.listSolvers(onlyAvailable=True))
# Количество вершин графа
n = 80
# random.seed(2)
points = [(round(random.randint(0, 1500)), round(random.randint(0, 1000))) for i in range(n)]
init_graph = nx.complete_graph(n)
for i, j in init_graph.edges():
if j > i:
init_graph[i][j]['weight'] = round(distance(points[i][0], points[i][1], points[j][0], points[j][1]))
# Развернуть граф как матрицу смежности
# adjacency_matrix = nx.adjacency_matrix(init_graph).todense()
# print(adjacency_matrix)
start_time = datetime.now()
# Создаём модель для решения
model = pl.LpProblem(name="tsp", sense=pl.LpMinimize)
#model = pl.LpProblem(name="tsp", sense=pl.LpMaximize)
# Подключаем решатель
solver = pl.PULP_CBC_CMD(msg=False) # Открытый, по умолчанию
# solver = pl.SCIP_CMD(msg=False) # Открытый, медленнее CBC
# solver = pl.CPLEX_PY(msg=False) # 45 Быстрый коммерческий (1000 Переменных)
# solver = pl.XPRESS_PY(msg=False) # ~98 Быстрый коммерческий (5000 Переменных + ограничений)
# solver = pl.GUROBI(msg=False) # 63 Быстрый коммерческий (2000 Переменных)
# Объявляем переменные
x = [pl.LpVariable(name=f'x_{i:03}_{j:03}', cat='Binary') for i in range(n) for j in range(n)]
# Задаём начальные ограничения
for i in range(n):
model += pl.lpSum([x[i * n + j if i < j else j * n + i] for j in range(n) if i != j]) == 2
# Устанавливаем целевую функцию
model += pl.lpSum([init_graph[i][j]['weight'] * x[i * n + j if i < j else j * n + i] for i in range(n) for j in range(n) if i < j])
step = 0
while True:
# Ищем решение
status = model.solve(solver)
step += 1
graph_resilt = nx.Graph()
a = 0
for i, v in enumerate(model.variables()):
# Приводим float от солвера к int
int_val = round(v.value())
if int_val > 0:
temp_name = v.name.split('_')
ii, jj = int(temp_name[1]), int(temp_name[2])
graph_resilt.add_edge(ii, jj)
# Разбиваем граф результата на подмножества
result_sets = list(nx.connected_components(graph_resilt))
qty_sets = len(result_sets)
print('Step =', step, 'Sets =', len(result_sets))
if qty_sets == 1:
break
if qty_sets == 2:
model += pl.lpSum([x[ii * n + jj if ii= 2
else:
for i, vi in enumerate(result_sets):
model += pl.lpSum([x[ii * n + jj if ii= 2
date_diff = (datetime.now() - start_time).total_seconds()
print('Time =', date_diff)
min_cycle = nx.find_cycle(graph_resilt, 0)
min_path = [i[0] for i in min_cycle]
# print(model)
print('Length =', round(model.objective.value()), 'steps =', step, 'path =', min_path)
plt.figure(figsize=(8, 6))
plt.axis ("equal")
nx.draw(init_graph, points, width=0, edge_color="#C0C0C0", with_labels=True, node_size=0, font_size=10)
nx.draw(graph_resilt, points, width=2, edge_color="red", style="-", with_labels=False, node_size=0, alpha=1)
plt.show() TSP CVXPY
#------------------------------------------------------------------------------------
# TSP_ILP - traveling salesman problem integer linear programming (ILP) method
# Решатель задачи комивояжора методом целочисленного линейного программирования
# Rebuilder 21.01.2023 https://habr.com/ru/publication/edit/711708/
#------------------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import cvxpy as cp
import random
import networkx as nx
from datetime import datetime
#------------------------------------------------------------------------------------
def distance(x1, y1, x2, y2):
# Расстояние между двумя точками на плоскости
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#------------------------------------------------------------------------------------
def to_flat_index(a, b):
# Возвращет плоский индекс для квадратной симметричной матрицы
summ = 0
if a >= b:
for i in range(1, a):
summ += i
return summ + b
else:
for i in range(1, b):
summ += i
return summ + a
#------------------------------------------------------------------------------------
def to_matrix_indexes(a):
# Возвращает кортеж индексов для квадратной симметричной матрицы по плоскому индексу
i = 0
while (a > i):
i += 1
a -= i
return (i+1, a)
#------------------------------------------------------------------------------------
def matrix_count(a):
# Возвращет размер плоского списка для квадратной симметричной матрицы
return((a * a - a) // 2)
#------------------------------------------------------------------------------------
print('Подключенные решатели:', cp.installed_solvers())
# Количество вершин графа
n = 80
# random.seed(3)
points = [(round(random.randint(0, 1500)), round(random.randint(0, 1000))) for i in range(n)]
init_graph = nx.complete_graph(n)
for i, j in init_graph.edges():
if j > i:
init_graph[i][j]['weight'] = round(distance(points[i][0], points[i][1], points[j][0], points[j][1]))
# Развернуть граф как матрицу смежности
# adjacency_matrix = nx.adjacency_matrix(init_graph).todense()
# print(adjacency_matrix)
start_time = datetime.now()
# Количество переменных
flat_size = matrix_count(n)
c = [0] * flat_size
# Устанавливаем переменные
for i in range(flat_size):
temp = to_matrix_indexes(i)
c[i] = init_graph[temp[1]][temp[0]]['weight']
x = cp.Variable(flat_size, boolean=True)
# Ограничения
constraints = []
for i in range(n):
constraints += [cp.sum([x[to_flat_index(i, j)] for j in range(n) if i != j]) == 2]
# Целевая функция
objective = cp.Minimize(cp.sum(c @ x))
step = 0
while True:
# Определяем задачу
prob = cp.Problem(objective, constraints)
# Ищем решение
prob.solve(solver = cp.GLPK_MI)
# prob.solve(solver=cp.SCIPY)
# prob.solve(solver = cp.CBC)
# prob.solve(solver = cp.XPRESS)
# print("status:", prob.status)
step += 1
graph_resilt = nx.Graph()
for i in np.argwhere(x.value == True):
temp = to_matrix_indexes(round(i[0]))
graph_resilt.add_edge(temp[1], temp[0])
# Разбиваем граф результата на подмножества
result_sets = list(nx.connected_components(graph_resilt))
qty_sets = len(result_sets)
print('Step =', step, 'Sets =', len(result_sets))
# Решение найдено
if qty_sets == 1:
break
# Добавочные ограничения
if qty_sets == 2:
constraints += [cp.sum([x[to_flat_index(i, j)] for i in result_sets[0] for j in result_sets[1]]) >= 2]
else:
for i, vi in enumerate(result_sets):
constraints += [cp.sum([x[to_flat_index(ii, jj)] for j, vj in enumerate(result_sets) if i != j for ii in vi for jj in vj]) >= 2]
date_diff = (datetime.now() - start_time).total_seconds()
print('Time =', date_diff)
min_cycle = nx.find_cycle(graph_resilt, 0)
min_path = [i[0] for i in min_cycle]
print('Length =', round(prob.value), 'steps =', step, 'path =', min_path)
plt.figure(figsize=(8, 6))
plt.axis ("equal")
nx.draw(init_graph, points, width=0, edge_color="#C0C0C0", with_labels=True, node_size=0, font_size=10)
nx.draw(graph_resilt, points, width=2, edge_color="red", style="-", with_labels=False, node_size=0, alpha=1)
plt.show()Так же предлагаю оценить собственную реализацию с использованием открытой библиотеки SciPy. В SciPy 1.10.0… (scipy.optimize.linprog) Появился замечательный целочисленный решатель.
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='highs', callback=None, options=None, x0=None, integrality=None)Задать его можно, скомбинировав опции: [method='highs', integrality=1].
Код выглядит сложноее. Такая задача со звёздочкой. Но и работает быстрее, чем варианты выше.
TSP SciPy
#------------------------------------------------------------------------------------
# TSP_ILP - traveling salesman problem integer linear programming (ILP) method
# Решатель задачи комивояжора методом целочисленного линейного программирования
# Rebuilder 21.01.2023 https://habr.com/ru/publication/edit/711708/
#------------------------------------------------------------------------------------
import numpy as np
from scipy import optimize
import random
import matplotlib.pyplot as plt
import networkx as nx
from datetime import datetime
#------------------------------------------------------------------------------------
def distance(x1, y1, x2, y2):
# Расстояние между двумя точками на плоскости
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#------------------------------------------------------------------------------------
def to_flat_index(a, b):
# Возвращет плоский индекс для квадратной симметричной матрицы
summ = 0
if a >= b:
for i in range(1, a):
summ += i
return summ + b
else:
for i in range(1, b):
summ += i
return summ + a
#------------------------------------------------------------------------------------
def to_matrix_indexes(a):
# Возвращает кортеж индексов для квадратной симметричной матрицы по плоскому индексу
i = 0
while (a > i):
i += 1
a -= i
return (i+1, a)
#------------------------------------------------------------------------------------
def matrix_count(a):
# Возвращет размер плоского списка для квадратной симметричной матрицы
return((a * a - a) // 2)
#------------------------------------------------------------------------------------
def TSP_ILP_cycle(graph, direction=1):
# Находит минимальный (максимальный) путь в графе методом целочисленного линейного программирования
# direction - Направление оптимизации: 1 Минимизировать путь, -1 Максимизировать путь
print('Run', end='')
# Количество вершин графа
n = len(graph.nodes())
# Количество переменных
flat_n = matrix_count(n)
# Целевая функция
objective_function = np.array([direction * graph[i][j]['weight'] for i in range(n) for j in range(n) if i > j], dtype=np.int32)
# Ограничение на диаппазон переменных
bounds = (0, 1)
# Объявление массивов ограничений
equality_a = np.zeros((n, flat_n), dtype=np.int8)
equality_b = np.array([2] * n, dtype=np.int8)
inequalities_a = np.zeros((0, flat_n), dtype=np.int8)
inequalities_b = np.zeros(0, dtype=np.int8)
# Начальные ограничения модели
for i in range(n):
for j in range(n):
if i != j:
equality_a[i][to_flat_index(i, j)] = 1
# Ищем опорное решение
res = optimize.linprog(c=objective_function, bounds=bounds, A_eq=equality_a, b_eq=equality_b, method='highs', integrality=1)
step = 1
constraints = 0
while True:
print('.', end='')
# Сохраняем результат в виде графа
graph_resilt = nx.Graph()
for i, val in enumerate(res.x):
# Приводим float от солвера к int
int_val = round(val)
if int_val == 1:
temp = to_matrix_indexes(i)
graph_resilt.add_edge(temp[1], temp[0])
# Разбиваем граф результата на подмножества
result_sets = list(nx.connected_components(graph_resilt))
qty_sets = len(result_sets)
# # Рисуем граф
# fig = plt.figure(figsize=(6.8, 4), edgecolor='black', linewidth=0)
# plt.title(f'Size: {n}; Length: {direction * round(res.fun)}; Steps: {step}; Constraints: {constraints}', fontsize=10)
# plt.axis("equal")
# nx.draw(graph, points, width=0, with_labels=True, node_size=0, font_size=6, font_color="black", node_shape='o')
# nx.draw(graph_resilt, points, width=1, edge_color="red", style="-", with_labels=False, node_size=0)
# Решение найдено если в графе только одно множество
if qty_sets == 1:
break
# Вводим дополнительные ограничения модели
if qty_sets == 2:
temp = np.zeros((1, flat_n), dtype=np.int8)
for i in result_sets[0]:
for j in result_sets[1]:
temp[0][to_flat_index(i, j)] = -1
inequalities_a = np.append(inequalities_a, temp, axis=0)
inequalities_b = np.append(inequalities_b, np.array([-2], dtype=np.int8))
constraints += 1
elif qty_sets > 2:
temp = np.zeros((qty_sets, flat_n), dtype=np.int8)
for i, vi in enumerate(result_sets):
for j, vj in enumerate(result_sets):
if i != j:
for ii in vi:
for jj in vj:
temp[i][to_flat_index(ii, jj)] = -1
inequalities_a = np.append(inequalities_a, temp, axis=0)
inequalities_b = np.append(inequalities_b, np.array([-2] * qty_sets, dtype=np.int8))
constraints += qty_sets
# Ищем уточненное решение
res = optimize.linprog(c=objective_function, bounds=bounds, A_eq=equality_a, b_eq=equality_b, A_ub=inequalities_a, b_ub=inequalities_b, method='highs', integrality=1)
step += 1
print()
return {'length' : direction * round(res.fun), 'constraints' : constraints, 'steps' : step, 'path' : [i[0] for i in nx.find_cycle(graph_resilt, 0)], 'graph' : graph_resilt}
#-----------------------------------------------------------------------------------
def TSP_ILP_path(graph, end_points=(), direction=1):
# Находит минимальный (максимальный) путь в графе методом целочисленного линейного программирования
# direction - Направление оптимизации: 1 Минимизировать путь, -1 Максимизировать путь
def get_end_points(li, n):
# Возвращает конечные точки пути
path = [0] * n
for i in li:
for j in i:
path[j] += 1
return [i for i, val in enumerate(path) if val == 1]
print('Run', end='')
# Количество вершин графа
n = len(graph.nodes())
# Количество переменных
flat_n = matrix_count(n)
# Определяем число заданных граничных вершин
end_points_n = 0
if len(end_points) > 0 and end_points[0] >= 0 and end_points[0] < n:
end_points_n += 1
if len(end_points) > 1 and end_points[1] >= 0 and end_points[1] < n and end_points[0] != end_points[1]:
end_points_n += 1
# Целевая функция
objective_function = np.array([direction * graph[i][j]['weight'] for i in range(n) for j in range(n) if i > j], dtype=np.int32)
# Ограничение на диаппазон переменных
bounds = (0, 1)
# Объявление массивов ограничений
equality_a = np.ones((1, flat_n), dtype=np.int8)
equality_b = np.zeros(1, dtype=np.int32)
inequalities_a = np.zeros(((n - end_points_n) * 2, flat_n), dtype=np.int8)
inequalities_b = np.zeros((n - end_points_n) * 2, dtype=np.int8)
# Начальные ограничения модели
equality_b[0] = n - 1
k = 0
for i in range(n):
# Если были заданы конечные точки, то исключаем их из неравенств для уменьшения условий
if (end_points_n > 0) and (end_points[0] == i) or (end_points_n > 1) and (end_points[1] == i):
continue
for j in range(n):
if i != j:
flat_index = to_flat_index(i, j)
inequalities_a[k][flat_index] = -1
inequalities_a[k + 1][flat_index] = 1
inequalities_b[k] = -1
inequalities_b[k + 1] = 2
k += 2
# Если были заданы конечные точки, то добавляем условиие на равенство единице в вершинах таких точек
if end_points_n > 0:
equality_a = np.append(equality_a, np.zeros((1, flat_n), dtype=np.int8), axis=0)
equality_b = np.append(equality_b, np.ones(1, dtype=np.int8))
for i in range(n):
if i != end_points[0]:
equality_a[1][to_flat_index(i, end_points[0])] = 1
if end_points_n > 1:
equality_a = np.append(equality_a, np.zeros((1, flat_n), dtype=np.int8), axis=0)
equality_b = np.append(equality_b, np.ones(1, dtype=np.int8))
for i in range(n):
if i != end_points[1]:
equality_a[2][to_flat_index(i, end_points[1])] = 1
# Ищем опорное решение
res = optimize.linprog(c=objective_function, bounds=bounds, A_eq=equality_a, b_eq=equality_b, A_ub=inequalities_a, b_ub=inequalities_b, method='highs', integrality=1)
step = 1
constraints = 0
while True:
print('.', end='')
# Сохраняем результат в виде графа
graph_resilt = nx.Graph()
for i, val in enumerate(res.x):
# Приводим float от солвера к int
int_val = round(val)
if int_val == 1:
temp = to_matrix_indexes(i)
graph_resilt.add_edge(temp[1], temp[0])
# Разбиваем граф результата на подмножества
result_sets = list(nx.connected_components(graph_resilt))
qty_sets = len(result_sets)
# Решение найдено если в графе только одно множество
if qty_sets == 1:
break
# Вводим дополнительные ограничения модели
if qty_sets == 2:
temp = np.zeros((1, flat_n), dtype=np.int8)
for i in result_sets[0]:
for j in result_sets[1]:
temp[0][to_flat_index(i, j)] = -1
inequalities_a = np.append(inequalities_a, temp, axis=0)
inequalities_b = np.append(inequalities_b, np.array([-2], dtype=np.int8))
constraints += 1
elif qty_sets > 2:
temp = np.zeros((qty_sets, flat_n), dtype=np.int8)
for i, vi in enumerate(result_sets):
for j, vj in enumerate(result_sets):
if i != j:
for ii in vi:
for jj in vj:
temp[i][to_flat_index(ii, jj)] = -1
inequalities_a = np.append(inequalities_a, temp, axis=0)
inequalities_b = np.append(inequalities_b, np.array([-2] * qty_sets, dtype=np.int8))
constraints += qty_sets
# Ищем уточненное решение
res = optimize.linprog(c=objective_function, bounds=bounds, A_eq=equality_a, b_eq=equality_b, A_ub=inequalities_a, b_ub=inequalities_b, method='highs', integrality=1)
step += 1
# Отображаем минимальный путь
ep = get_end_points(graph_resilt.edges, n)
path = list(nx.all_simple_paths(graph_resilt, ep[0], ep[1]))[0]
print()
return {'length' : direction * round(res.fun), 'constraints' : constraints, 'steps' : step, 'path' : path, 'graph' : graph_resilt}
#-----------------------------------------------------------------------------------
# Количество вершин графа
n = 80
# random.seed(4)
points = [(round(random.randint(0, 15000)), round(random.randint(0, 10000))) for i in range(n)]
init_graph = nx.complete_graph(n)
for i, j in init_graph.edges():
if j > i:
init_graph[i][j]['weight'] = round(distance(points[i][0], points[i][1], points[j][0], points[j][1]))
# Развернуть граф как матрицу смежности
# adjacency_matrix = nx.adjacency_matrix(init_graph).todense()
# print(adjacency_matrix)
start_time = datetime.now()
# Запускаем расчёт замкнутой TSP
res = TSP_ILP_cycle(init_graph, direction=1)
# Запускаем расчёт незамкнутой TSP
# res = TSP_ILP_path(init_graph, end_points=[], direction=1)
date_diff = (datetime.now() - start_time).total_seconds()
print('Time =', date_diff)
print('Path =', res['path'])
# Рисуем граф
fig = plt.figure(figsize=(6.8, 4), edgecolor='black', linewidth=0)
plt.title(f'Size: {n}; Length: {res["length"]}; Steps: {res["steps"]}; Constraints: {res["constraints"]}', fontsize=10)
plt.axis("equal")
nx.draw(init_graph, points, width=0, with_labels=True, node_size=0, font_size=6, font_color="black", node_shape='o')
nx.draw(res["graph"], points, width=1, edge_color="red", style="-", with_labels=False, node_size=0)Теперь о грустном. Вся сложность вычислений ложится на решатель линейных уравнений. От его качества зависит приктически всё. Как я понимаю, в среднем решение находится как O (n^3) от числа вершин. К сожалению, есть и плохие случаи, когда решение падает до O (2^n). Целочисленное программирование является NP-трудной задачей. Следовательно задача коммивояжёра остаётся NP-трудной, несмотря на то, что мы немного снизили асимптоматику задачи.
Эвристические методы (генетический и муравьиный алгоритмы) конечно обходят текущую реализацию алгоритма по скорости нахождения решения, но зато грешат в точности.
Что даёт нам точное решение проблемы коммивояжёра? Как мне видится, кроме очевидного решения транспортной задачи, наибольший выигрыш может получить схемотехника / материалообработка.
На печатной плате нужно просверлить монтажные отверстия (произвести пайку / прочее действие), в какой последовательности нужно обходить точки контакта, чтобы максимально сократить время на перемещение рабочего инструмента? Задача коммивояжёра в чистом виде.
Полагаю, что сам подход полученный в ходе решения данной задачи может помочь найти ключ к решению других задач класса NP.
P.S. Создать эту работу было NP-трудно, надеюсь она вам понравилась.
