Зачем менять надёжный пароль? Брутфорс и энтропия07.11.2022 04:02

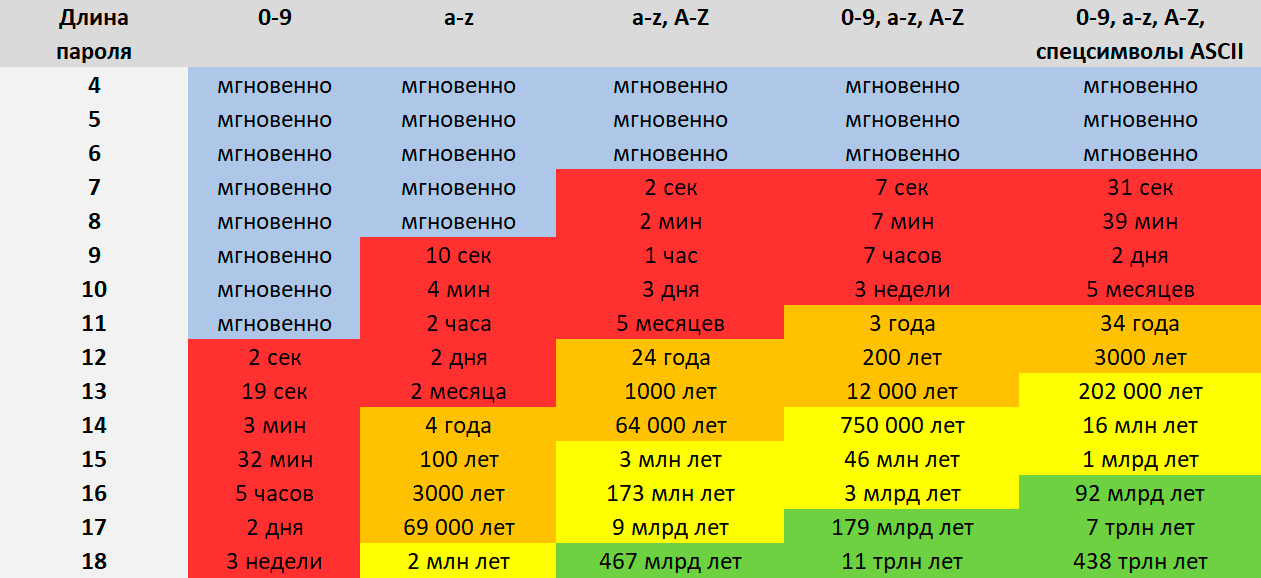
Что такое надёжный пароль? По мере развития технологий за последние десятилетия несколько раз менялись политика, что считать таковым. Мощности для брутфорса становятся всё доступнее, в том числе в облаках, поэтому и требования к энтропии паролей повышаются — в 2022 году рекомендуется использовать спецсимволы, цифры, буквы в разных регистрах, с общей длиной минимум 11 символов.

Недавно в индустрии информационной безопасности поднялась дискуссия на тему смены паролей. В частности, появились рекомендации против периодической смены паролей. Логика в том, что пользователям сложнее учить новые пароли каждую неделю, чем запомнить один большой и сложный пароль. В 2017 году рекомендации против смены паролей опубликовала организация NIST, отвечающая за принятие стандартов парольной защиты.

Рекомендации NIST

Пароль представляет собой шаблон, слово, комбинацию или другой тип информации, который предположительно известен только пользователю и может быть проверен для подтверждения личности пользователя.

Стандарты и определения о парольной защите изложены в Специальной публикации NIST 800–63B, раздел 5.1.1.2 «Запоминаемые секретные верификаторы» (NIST, 2017).

В 2017 году NIST официально заявила, что обязательная смена пароля на самом деле значительно снижает общую безопасность системы паролей и не должна использоваться. Это объясняется в вопросах B05 и B06 в разделе FAQ документации NIST к обновлённым специальным публикациям (NIST, 2020).

Но на самом проведено крайне мало исследований, подтверждающих тезис NIST о снижении энтропии паролей при их периодической смене. Давайте разберёмся, так ли это на самом деле.

Энтропия и брутфорс

Для вычисления энтропии (E) пароля используется формула

Расчёт количества попыток (G), необходимых для подбора пароля с вероятностью 50%, производится по формуле

• S — размер пула уникальных символов. Некоторые составляющие пула:
  • цифры (0–9): 10
    
  • строчные символы латинского алфавита (a-z): 26
    
  • строчные и прописные символы латинского алфавита (a-z, A-Z): 52
    
  • набор символов ASCII (a-z, A-Z, символы, space): 95
• L — длина пароля

Чем выше энтропия — тем лучше, а по современным меркам достаточной считается энтропия 36 бит. Например, пароль типа S@mp1ePas$word состоит из строчных и прописных букв, цифр и специальных символов ASCII длиной 14 символов. Такая комбинация даёт размер пула 95, и по формуле это соответствует примерно 4,87×1027 возможным комбинациям пароля.

Энтропия такого пароля будет рассчитана как , то есть примерно 91,98 бит. С таким значением энтропии мы можем примерно рассчитать, сколько попыток в среднем понадобится, чтобы подобрать пароль (брутфорс 50% всех возможных вариантов). По формуле мы получаем 291,98–1, то есть примерно 2,44×1027 случайных попыток.

Это общее описание метода. В реальности злоумышленник может значительно уменьшить количество попыток с помощью словаря. Для сохранения нормальной энтропии критически важно генерировать случайные пароли в специальном программном обеспечении со стойким ГПСЧ, а не вручную.

Но в целом в индустрии принято мнение, что энтропия пароля, вычисленная по такой методике, коррелирует с его безопасностью.

Для сравнения, у пароля длиной восемь символов из строчных букв энтропия всего лишь 37,6 бит, что даёт нам среднее количество попыток 104,2 млрд. Если предположить, что компьютерная система перебирает более ста миллиардов вариантов в секунду, то такой пароль она взломает практически мгновенно даже без помощи словаря.

Периодическая смена паролей повышает энтропию

Группа исследователей из Университета Роберта Морриса (США) задалась вопросом, насколько эффективной является периодическая смена паролей. В частности, они решили проверить, насколько понижается или повышается энтропия в этом процессе.

Исследователи поставили небольшой эксперимент, в котором согласились участвовать 51 доброволец из тематических сообществ r/PCMasterRace, r/SysAdmin и r/CyberSecurity, где общаются энтузиасты компьютерных технологий.

Краткое описание эксперимента:

1. Участников попросили создать аккаунт на сайте эксперимента и придумать произвольный пароль от 2 до 160 символов.
2. Затем они дважды в неделю в течение двух месяцев входили в учётную запись. Вход был необходим, чтобы проверить, помнят ли участники свой пароль и могут ли они использовать его в течение длительного периода времени.
3. В каждую пятницу пользователям предлагалось выполнить задание в зависимости от их подгруппы. Членам группы А для выполнения задания нужно было просто войти в систему без смены пароля. Членам группы В предлагалось сменить пароль каждую пятницу, а членам группы С — каждую вторую пятницу.

Система была запрограммирована на автоматическую регистрацию всех попыток входа в систему, как успешных, так и неуспешных. Система также автоматически записывала все значения энтропии пароля при каждом обновлении или сбросе пароля. Эти показатели были разработаны для того, чтобы зафиксировать, была ли у какой-либо конкретной группы более высокая частота неудачных попыток входа в систему или других ошибок при входе, а также для отслеживания участия пользователей в исследовании с течением времени.

Был написан скрипт для безопасного вычисления энтропии паролей на хосте без раскрытия или сохранения фактического значения пароля в открытом виде.

По окончании эксперимента получены следующие результаты энтропии (до конца эксперимента продержались 28 человек):
Финальный опрос пользователей из трёх контрольных групп показал, что примерно половина из них использует парольный менеджер, а каждый третий использует предсказуемый паттерн при создании нового пароля.

Тем не менее авторы делают вывод, что периодическая смена пароля скорее повышает, а не понижает их энтропию, как предполагала NIST. Хотя с учётом ограниченного размера выборки, для подтверждения найденных закономерностей необходимо провести дополнительные исследования.

Результаты исследования опубликованы в апреле 2022 года в журнале «Проблемы информационных систем» (том 23:2, стр. 29–41, doi: 10.48009/2_iis_2022_10).

© Habrahabr.ru